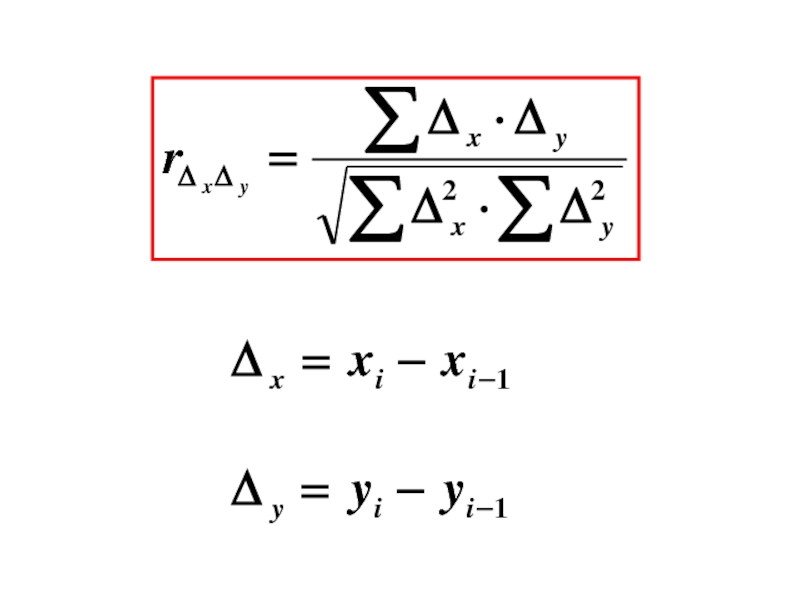- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
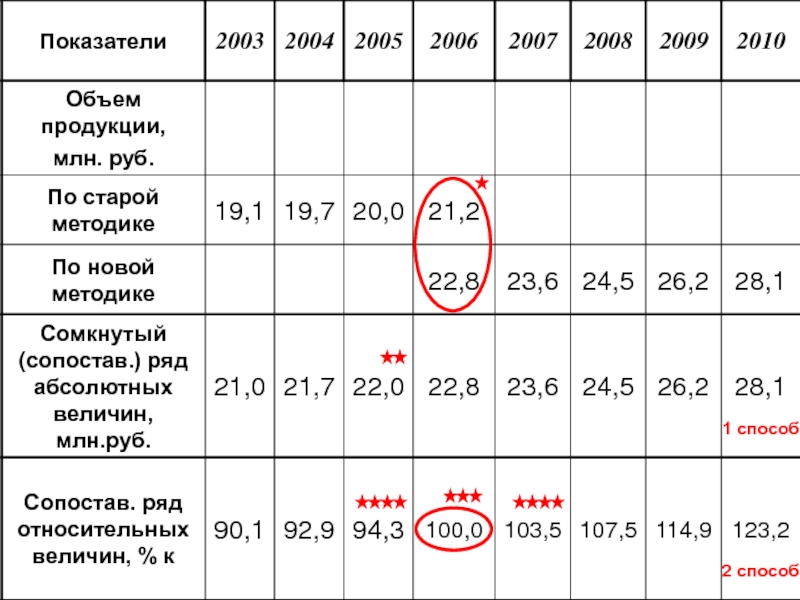
Статистическое изучение динамики социально - экономических явлений презентация
Содержание
- 1. Статистическое изучение динамики социально - экономических явлений
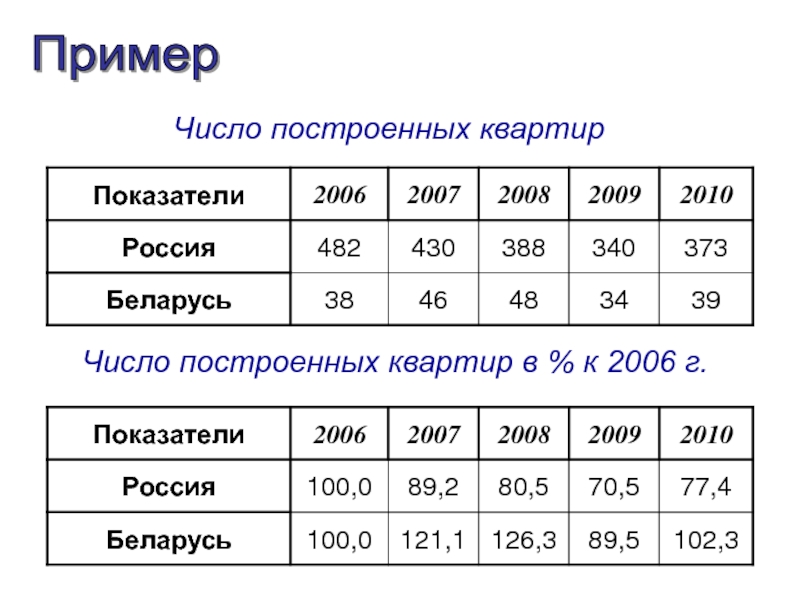
- 4. Число построенных квартир Число построенных квартир в % к 2006 г. Пример
- 5. Коэффициент опережения/замедления Применяется, когда ряд представляет
- 6. Средние темпы роста для Белоруссии – 100,33%,
- 7. 1 2 3 4 5
- 8. Абсолютный прирост или – уровень i-ого
- 9. Коэффициент роста (темп роста) или 3
- 10. Коэффициент (темп) прироста или 4 Также: Может быть: положительным, отрицательным, равным 0 или
- 11. Абсолютное значение 1% прироста или 5
- 12. Абсолютное ускорение Показывает, на сколько данная скорость больше/меньше предыдущей Может быть: положительным, отрицательным числом
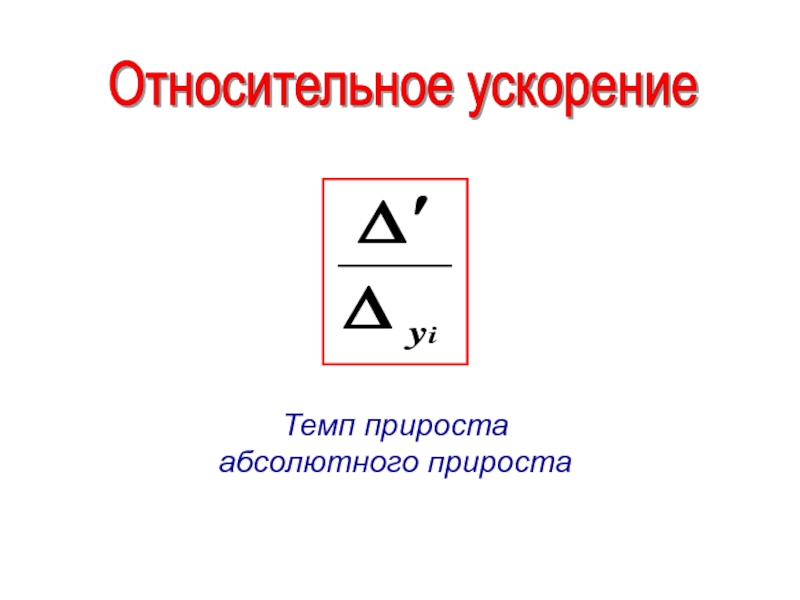
- 13. Относительное ускорение Темп прироста абсолютного прироста
- 14. Пример: Для ряда: 30, 33, 35,
- 15. Методы расчета среднего уровня ряда Для
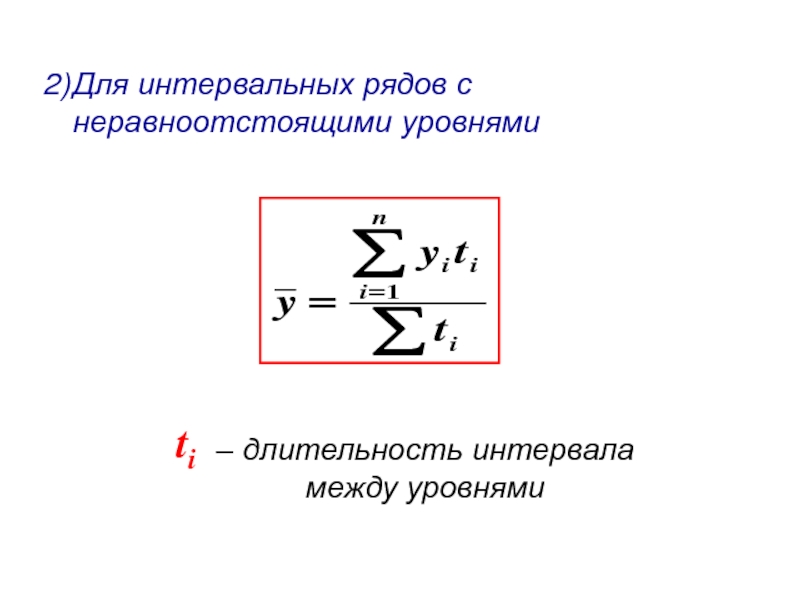
- 16. Для интервальных рядов с неравноотстоящими уровнями – длительность интервала между уровнями ti
- 17. Для моментного ряда с равноотстоящими уровнями или
- 18. Для моментного ряда с неравноотстоящими уровнями или – уровни рядов динамики yi , yn
- 19. Пример: Известны товарные остатки магазина на 1ое число каждого месяца, тыс.руб.: 1 способ: тыс.руб.
- 20. 2 способ: тыс.руб. Предполагается непрерывное, равномерное изменение
- 21. Пример: Известна списочная численность рабочих организаций на некоторые даты 2008г., чел.: чел.
- 22. Средний абсолютный прирост Возможен расчет, исходя из кумулятивных данных: или
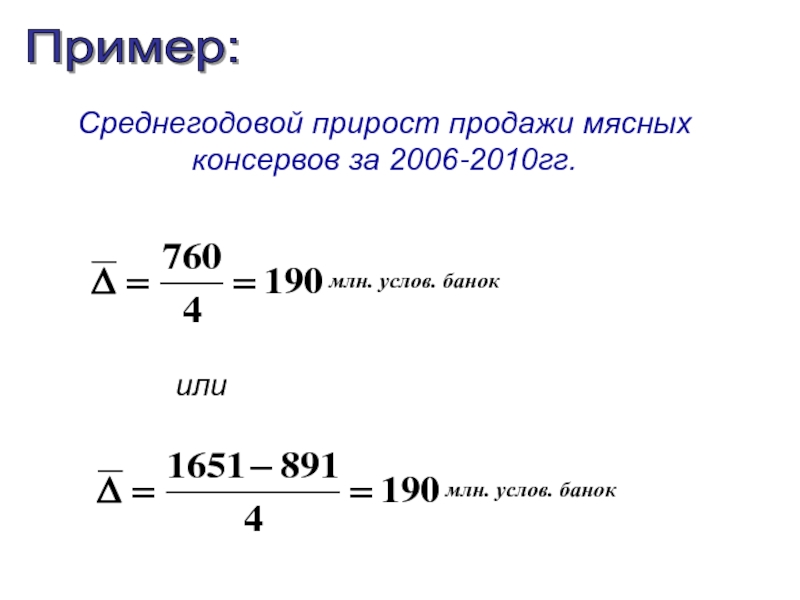
- 23. Пример: Среднегодовой прирост продажи мясных консервов
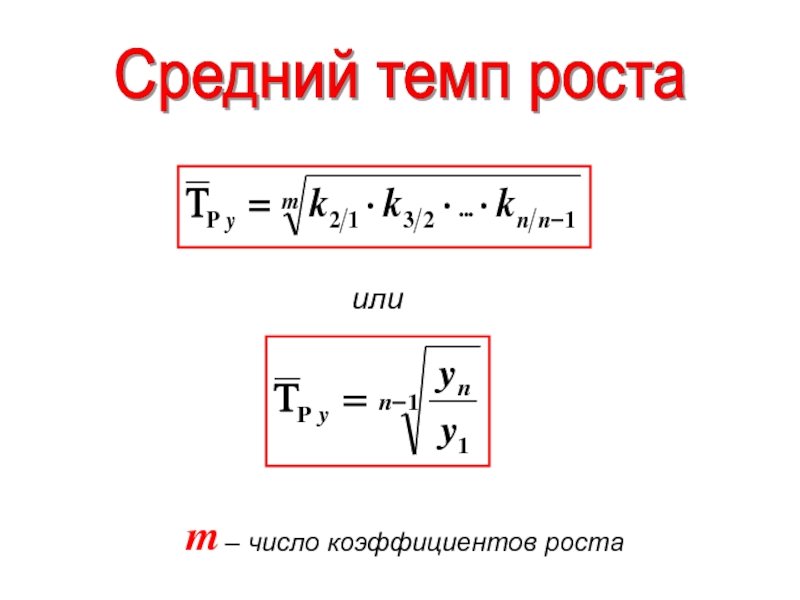
- 24. Средний темп роста или m – число коэффициентов роста
- 25. Пример: Средний темп роста продажи мясных консервов за 2006-2010гг. или
- 26. При разноотстоящих рядах используется: Средний темп роста
- 27. Получается уменьшением среднего темпа роста на 1 или 100% Средний темп прироста
- 28. Пример: Средний темп прироста продажи мясных консервов за 2006-2010гг.
- 29. Метод проверки существенности разности средних Методы выявления наличия тенденции Метод Фостера-Стюарта
- 30. Сравнивается каждый уровень ряда со всеми предыдущими,
- 31. Вычисляются значения величин S и d: Характеризует
- 32. Проверяется с использованием t-критерия Стьюдента гипотеза о
- 33. Сравниваются расчетные значения ts и td с
- 34. 1 6
- 35. уровень значимости – 0,10
- 36. Методы сглаживания Метод усреднения по левой
- 37. Алгоритм расчета 1) Определить интервал сглаживания, т.е. число входящих в него уравнений m (m
- 38. Алгоритм расчета 2) Вычислить среднее значение уравнений, образующих интервал сглаживания: или
- 39. yi – фактическое значение i-ого уровня
- 40. Алгоритм расчета 3) Сдвинуть интервал сглаживания
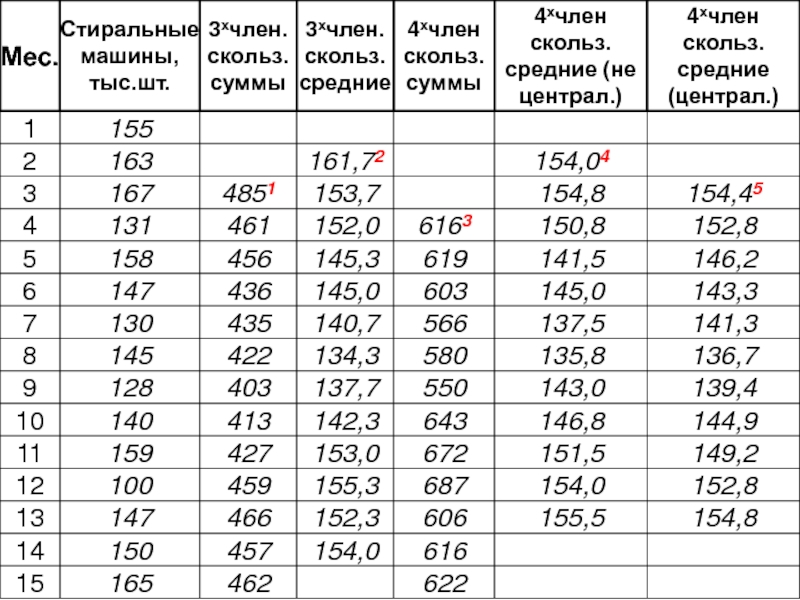
- 42. 1 2 3 4 5 Расчеты:
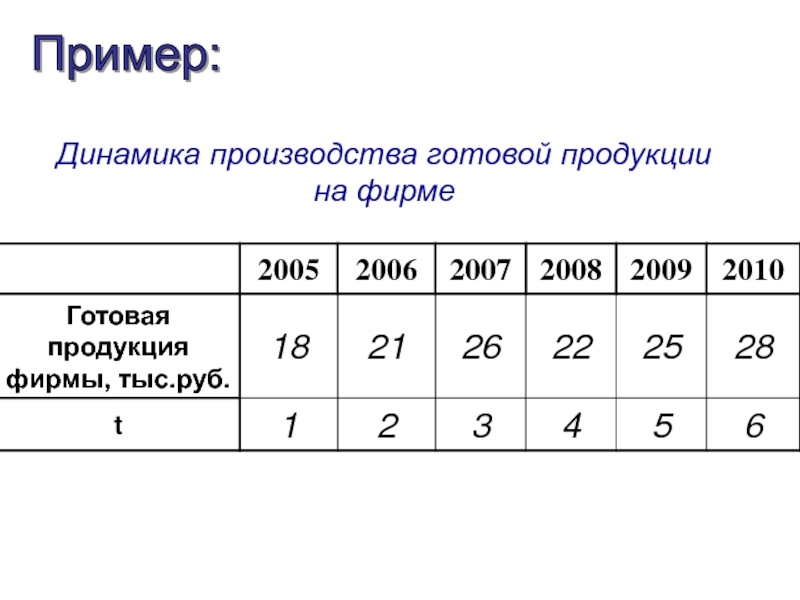
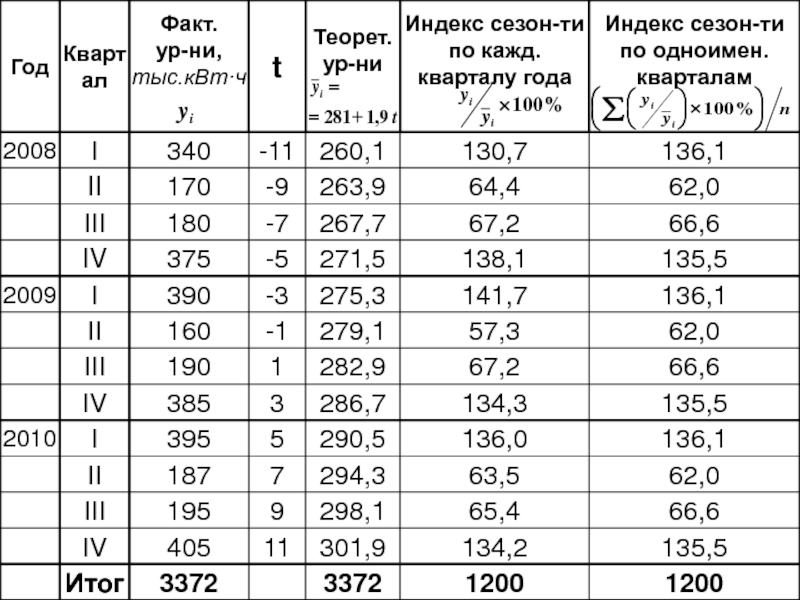
- 43. Динамика производства готовой продукции на фирме Пример:
- 44. Приняв условные обозначения времени через t и
- 45. Развитие по параболе 2-ого порядка:
- 46. Выравнивание ряда динамики с помощью метода конечных разностей
- 47. Вычисляем 1ые разности: 2ые разности: Окончательная формула
- 49. 1 2 3 Расчеты:
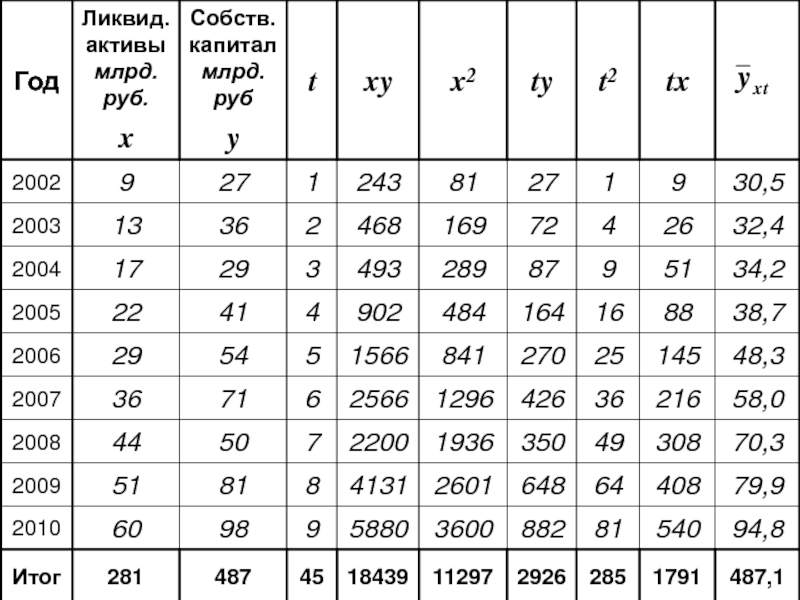
- 50. Аналитическое выравнивание
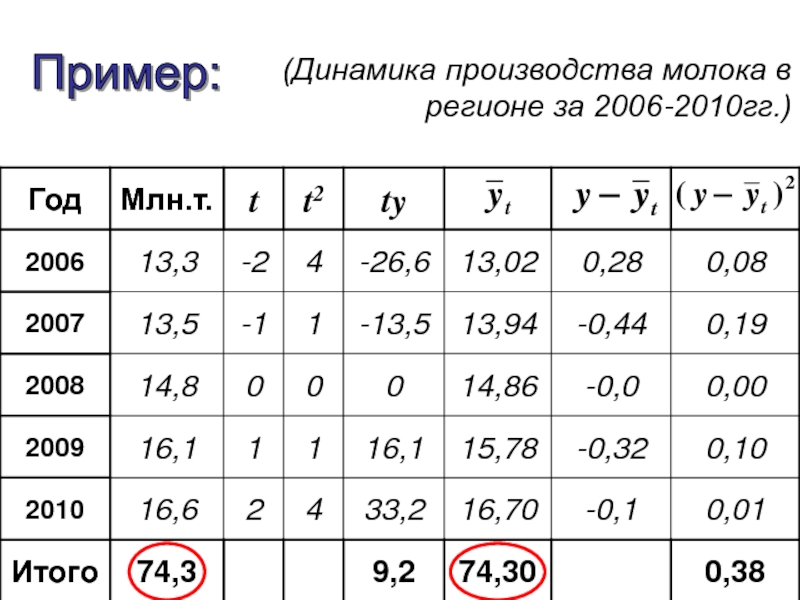
- 51. Пример: (Динамика производства молока в регионе за 2006-2010гг.)
- 52. Уравнение прямой: Система нормальных уравнений по способу наименьших квадратов:
- 53. - средний уровень ряда 2006: 2007:
- 54. Если число уровней ряда четное: (счет времени ведется полугодиями)
- 55. Колеблемость уравнений около тренда Служит мерой воздействия остаточных факторов
- 56. Пример: (Показатель колеблемости производства молока в регионе) млн.т.
- 57. Коэффициент вариации Является относительной мерой колеблемости
- 58. Пример: (Относительный показатель колеблемости производства молока в регионе)
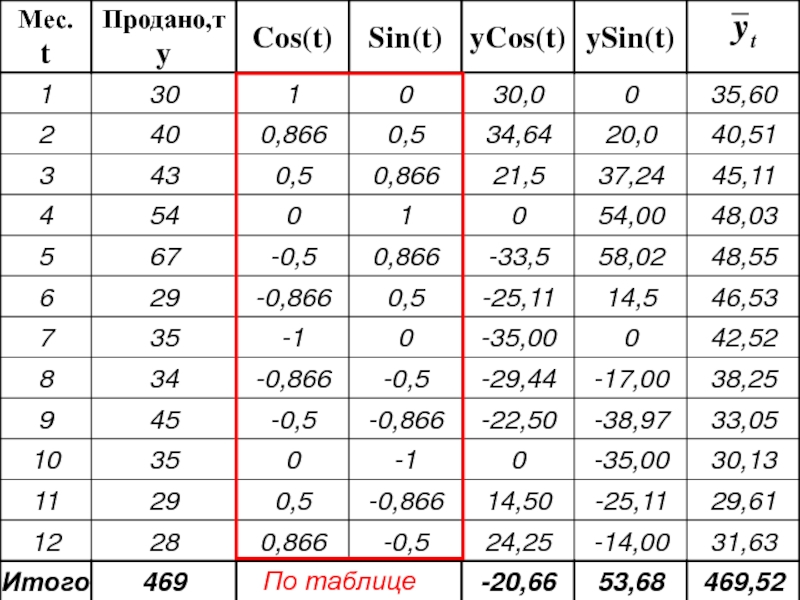
- 59. Гармонический анализ
- 60. k – степень точности гармоники тригонометрического многочлена
- 61. По методу наименьших квадратов:
- 62. Для изучения сезонности n=12 (по числу месяцев в году)
- 63. По таблице
- 66. Аналогично рассчитываются гармоники 2-ого и высших порядков
- 67. Рассчитав остаточные дисперсии для всех гармоник,
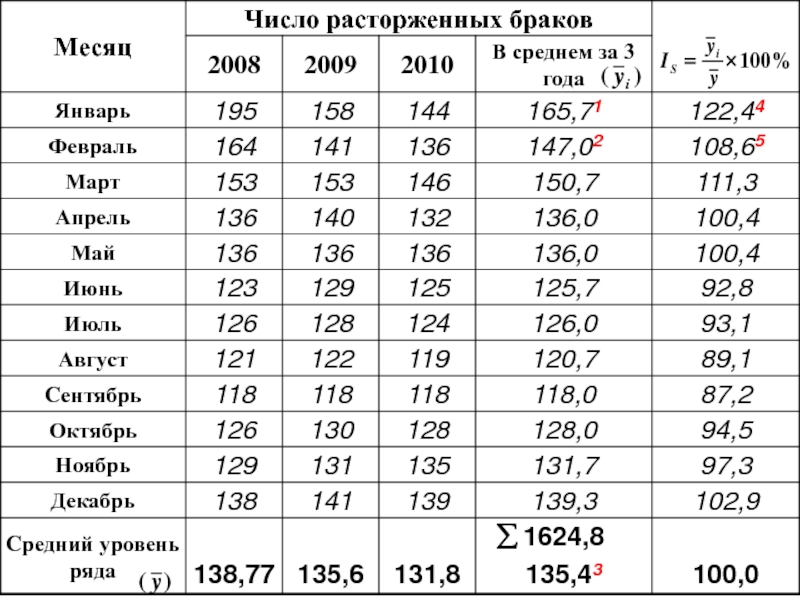
- 68. Сезонные колебания
- 69. Индексы сезонности – средняя величина уровня – среднемесячный уровень для всего ряда
- 71. 1 2 3 или m - число лет
- 72. 4 5 янв.: февр.:
- 73. Алгоритм расчета 1) Вычислить для каждого
- 74. Алгоритм расчета 2) Определить отклонения фактических
- 75. Алгоритм расчета 3) Найти среднее арифметическое
- 76. Алгоритм расчета 5) Определить индексы сезонности по формуле: или
- 78. I: II: Проверка:
- 79. I % квартал II III IV
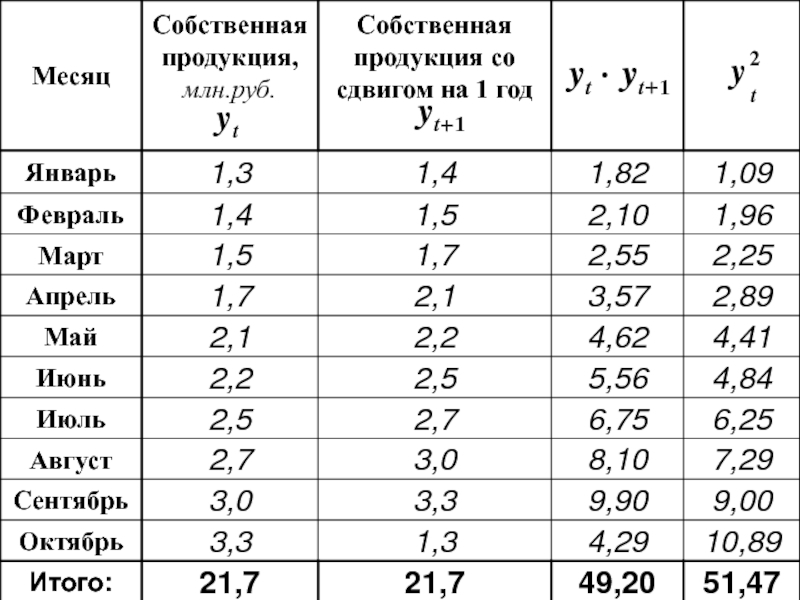
- 80. Автокорреляция Измеряется с помощью нециклического коэффициента автокорреляции
- 81. Если yn = y1, то yt = yt+1 ; или
- 82. Если y = 0
- 85. По «Таблице 5%-ого и 1%-ого уравнений вероятности
- 86. Способ выявления автокорреляции в отклонениях от тренда или от регрессионной модели
- 87. Критерий Дарбина -Уотсона:
- 88. Автокорреляция отрицательная Автокорреляция положительная Всегда ближе к
- 90. - Положительная автокорреляция
- 91. Исключение или уменьшение автокорреляции в рядах динамики
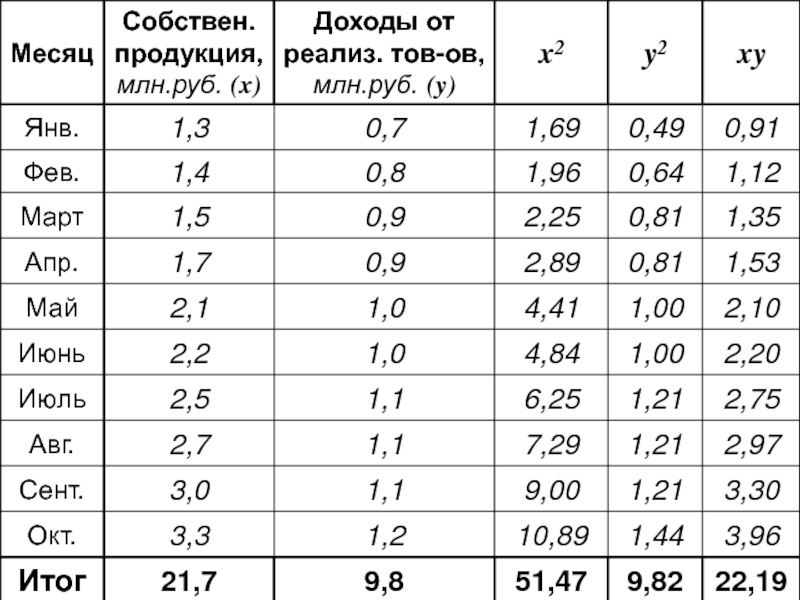
- 94. Расчет парного коэффициента корреляции по уровням ряда динамики
- 96. Связь прямая сильная
- 97. Расчет парного коэффициента корреляции по отклонениям фактических уровней от выровненных по тренду
- 98. 1) Каждый ряд динамики выравнивают по определенной,
- 99. 3) Определяют тесноту связи между рассчитанными отклонениями (dx и dy) по формуле:
- 100. Расчет парного коэффициента корреляции по абсолютным отклонениям уровней ряда динамики
- 102. Коэффициент автокорреляции для остаточных величин
- 103. Прогнозирование - прогнозируемый уровень - текущий
- 104. Прогнозирование по среднему абсолютному приросту
- 105. - экстраполяционный уровень - срок прогноза - средний абсолютный прирост - номер этого уровня (года)
- 106. Использование среднего абсолютного прироста возможно только при следующем условии:
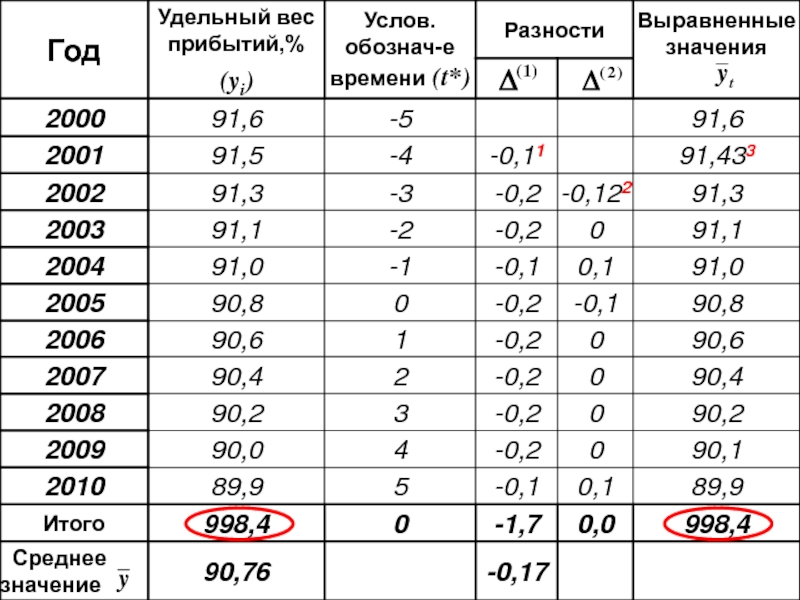
- 107. Пример: По данным об удельном весе
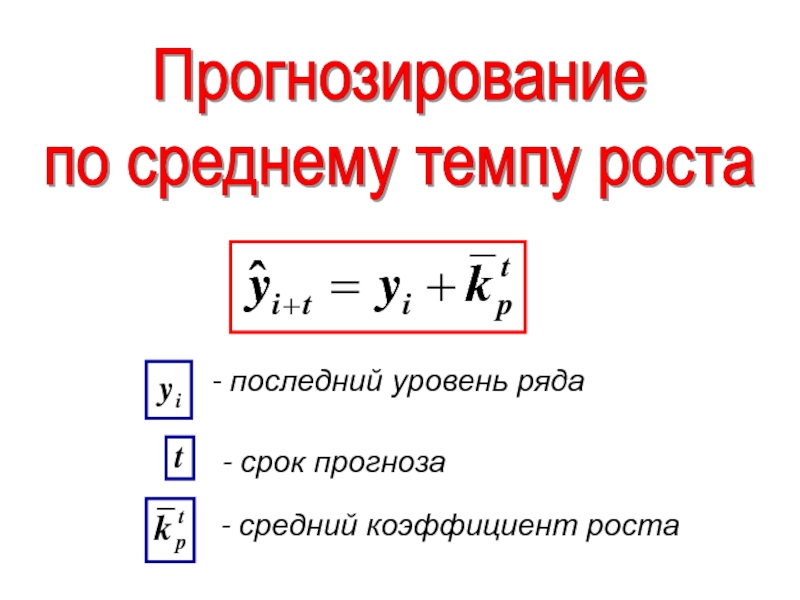
- 108. Прогнозирование по среднему темпу роста -
- 109. Доверительные интервалы прогноза - число параметров адекватной модели тренда
- 110. - средняя квадратичная ошибка тренда доверительная
1 способ 2 способ
Слайд 5Коэффициент опережения/замедления
Применяется, когда ряд представляет постоянное повышение
Применяется, когда нет ярко-выраженной
тенденции к росту
Слайд 6Средние темпы роста для Белоруссии – 100,33%,
для России – 96,41%
Пример
В
2010г. по сравнению с 2006г. число построенных квартир в Белоруссии было в 1,04 раза больше, чем в России
Слайд 8Абсолютный прирост
или
– уровень i-ого года
yi
y1
– уровень базисного года
млн. услов. банок
млн.
услов. банок
1
2
Слайд 11Абсолютное значение 1% прироста
или
5
Показывает, сколько абсолютных единиц приходится на 1
% прироста (уменьшения)
или
млн. услов. банок
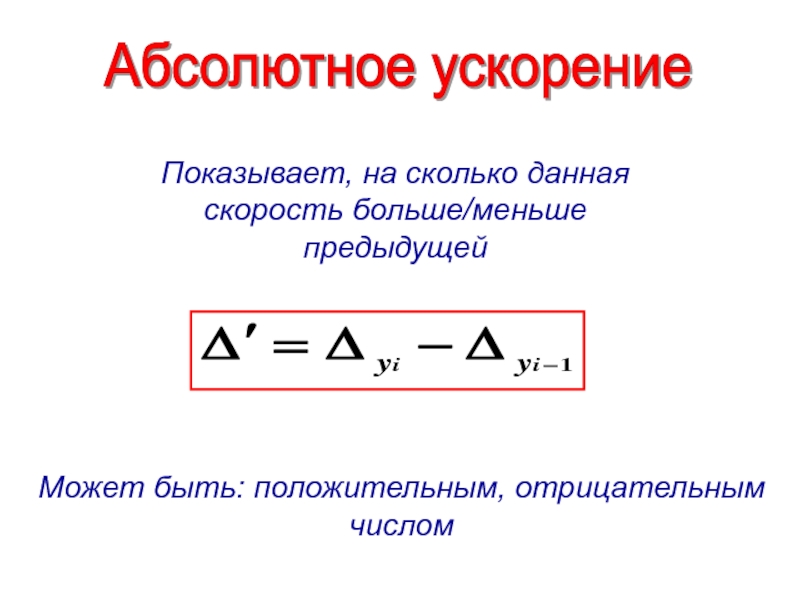
Слайд 12Абсолютное ускорение
Показывает, на сколько данная скорость больше/меньше предыдущей
Может быть: положительным,
отрицательным числом
Слайд 14Пример:
Для ряда: 30, 33, 35, 39, 44
Абсолютные приросты: 3, 2,
4, 5
Абсолютные ускорения: –1, 2, 1
Относительные ускорения: (–1/3)*100%= –33,3%
(2/2)*100%= 100%
(1/4)*100%= 25%
Абсолютные ускорения: –1, 2, 1
Относительные ускорения: (–1/3)*100%= –33,3%
(2/2)*100%= 100%
(1/4)*100%= 25%
Слайд 15Методы расчета среднего уровня ряда
Для интервальных рядов с равноотстоящими уровнями
n
–
число наблюдений
– уровень ряда динамики
yi
Слайд 16Для интервальных рядов с неравноотстоящими уровнями
– длительность интервала между уровнями
ti
Слайд 19Пример:
Известны товарные остатки магазина на 1ое число каждого месяца, тыс.руб.:
1
способ:
тыс.руб.
Слайд 202 способ:
тыс.руб.
Предполагается непрерывное, равномерное изменение уровня в промежутках между 2мя датами
январь
февраль
март
Слайд 21Пример:
Известна списочная численность рабочих организаций на некоторые даты 2008г., чел.:
чел.
Слайд 23Пример:
Среднегодовой прирост продажи мясных консервов за 2006-2010гг.
млн. услов. банок
млн. услов.
банок
или
Слайд 26При разноотстоящих рядах используется:
Средний темп роста
– интервал, в течении которого
сохраняется данный темп роста
– сумма отрезков периода
Слайд 29Метод проверки существенности разности средних
Методы выявления наличия тенденции
Метод Фостера-Стюарта
Слайд 30Сравнивается каждый уровень ряда со всеми предыдущими, при этом:
если
то
если
то
Метод Фостера-Стюарта
Слайд 31Вычисляются значения величин S и d:
Характеризует тенденцию изменения дисперсии ряда
Характеризует изменение
тенденций в среднем
Метод Фостера-Стюарта
Слайд 32Проверяется с использованием t-критерия Стьюдента гипотеза о том, можно ли считать
случайными разности S-M и d-0:
– среднее значение величины S, определенное для ряда, в котором уровни расположены случайным образом
и
– стандартные ошибки величин S и d соответственно
Метод Фостера-Стюарта
Слайд 33Сравниваются расчетные значения ts и td с табличными при заданном уровне
значимости
Метод Фостера-Стюарта
Гипотеза об отсутствии тренда в средней и дисперсии подтверждается
Слайд 36Методы сглаживания
Метод усреднения по левой и правой половине
Метод укрупнения интервалов
Метод
скользящей средней
Слайд 37Алгоритм расчета
1) Определить интервал сглаживания, т.е. число входящих в него
уравнений m (m
Если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берут большим (и наоборот)
Слайд 38Алгоритм расчета
2) Вычислить среднее значение уравнений, образующих интервал сглаживания:
или
Слайд 39yi – фактическое значение i-ого уровня
yt – текущий уровень ряда
динамики
i – порядковый номер уровня в интервале сглаживания
m – число уровней, входящих в интервал сглаживания (m=2p+1)
p – при нечетной m равно: p=(m-1)/2
Слайд 40Алгоритм расчета
3) Сдвинуть интервал сглаживания на 1 точку вправо, вычислить
сглаженное значение для t+1 члена, снова произвести сдвиг и т.д.
В результате получится n-(m-1) новых сглаженных уровней
Слайд 44Приняв условные обозначения времени через t и взяв 2 точки –
конечный и начальный уровни, можно построить уравнение прямой по этим 2м точкам;
Слайд 47Вычисляем 1ые разности:
2ые разности:
Окончательная формула
для расчета уровней ряда
при равных или
почти равных 1ых разностях:
Слайд 60k – степень точности гармоники тригонометрического многочлена
t – время
выражается в
радиальной мере
определяется от 0 с приростом 2П/n (n – число уравнений ряда)
определяется от 0 с приростом 2П/n (n – число уравнений ряда)
Слайд 67Рассчитав остаточные дисперсии для всех гармоник,
можно сделать вывод, какая гармоника
ряда Фурье наиболее близка к фактическим уровням ряда.
Слайд 73Алгоритм расчета
1) Вычислить для каждого месяца (квартала) выравненные уровни по
соответствующему аналитическому уровню на момент времени t
Слайд 74Алгоритм расчета
2) Определить отклонения фактических месячных (квартальных) данных к соответствующим
выравненным данным в %:
Слайд 75Алгоритм расчета
3) Найти среднее арифметическое из процентных соотношений, рассчитанных по
одноименным периодам в %
n – число одноименных периодов
Слайд 85По «Таблице 5%-ого и 1%-ого уравнений вероятности коэффициентов корреляции»
n=10
p=0,05 ra=0,36
0,48 > 0,36
Наличие автокорреляции
Слайд 88Автокорреляция отрицательная
Автокорреляция положительная
Всегда ближе к 2 (при условии, что отклонения уровней
от тенденции, остатки, случайны)
Слайд 97Расчет парного коэффициента корреляции по отклонениям фактических уровней от выровненных по
тренду
Слайд 981) Каждый ряд динамики выравнивают по определенной, характерной для него аналитической
формуле
2) Из эмпирических уравнений вычитают выравненные:
Слайд 103Прогнозирование
- прогнозируемый уровень
- текущий уровень прогнозируемого ряда
период упреждения
(срок экстраполяции)
- параметр
уровня тренда
Слайд 105- экстраполяционный уровень
- срок прогноза
- средний абсолютный прирост
- номер этого уровня
(года)
Слайд 107Пример:
По данным об удельном весе прибытия воздушных судов, выполненных без
опоздания по сравнению с расписанием за 2000-2010гг.
экстраполируем ряд на 2011-2012гг.
экстраполируем ряд на 2011-2012гг.
Слайд 108Прогнозирование по среднему темпу роста
- последний уровень ряда
- срок прогноза
-
средний коэффициент роста
Слайд 110- средняя квадратичная ошибка тренда
доверительная величина по распределению Стьюдента
(t-распределение)
- расчетное
значение уровня
