- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические распределения и их основные характеристики презентация
Содержание
- 1. Статистические распределения и их основные характеристики
- 2. Различия индивидуальных значений признака у единиц совокупности
- 3. Вариация, которая не зависит от
- 4. Изучение вариации в пределах одной группы предполагает
- 5. Вариационный ряд - групповая таблица, построенная по
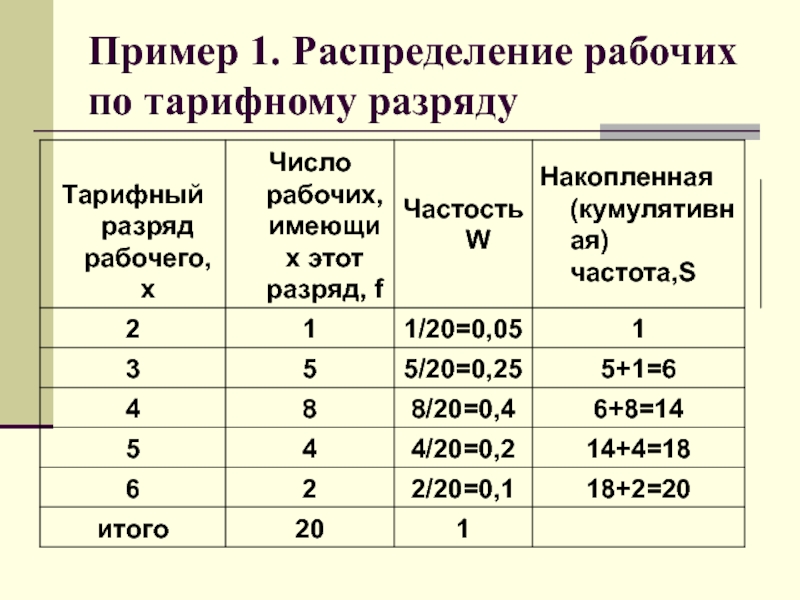
- 6. Пример 1. Распределение рабочих по тарифному разряду
- 7. Частость расчитывается по формуле
- 8. Средняя квалификация работников
- 9. Для признака, имеющего непрерывное изменение строится интервальный
- 10. Показатели центра распределения. Средняя арифметическая для дискретного ряда расчитывается по формуле средней арифметической взвешенной:
- 11. В интервальном ряду расчет производится по
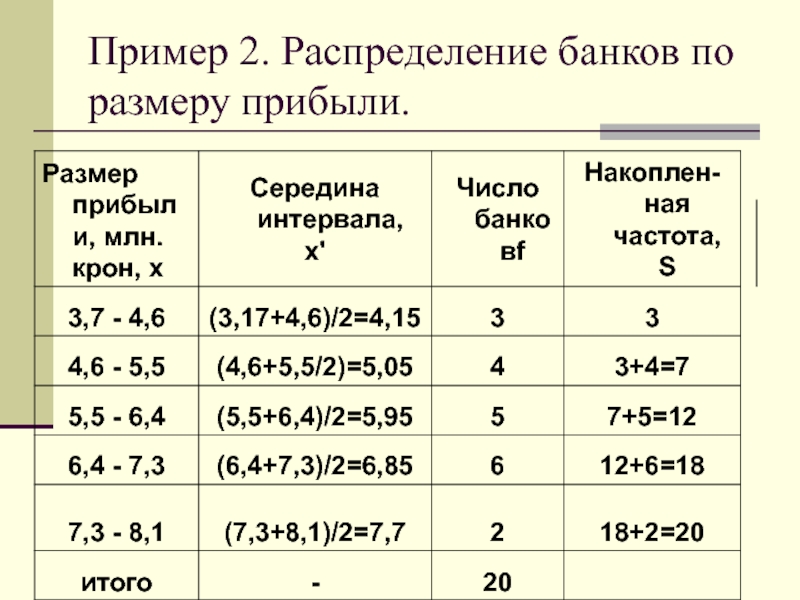
- 12. Пример 2. Распределение банков по размеру прибыли.
- 13. Средний размер прибыли
- 14. Мода (Мо) наиболее часто встречающееся значение
- 15. Значение моды определяется по формуле:
- 16. В примере 1 наибольшую частоту -
- 17. Медиана (Ме) соответствует варианту, стоящему в
- 18. Медиана в дискретном ряду По накопленным частотам
- 19. Следовательно, среднее значение 10-го и 11-го
- 20. Медиана в интервальном ряду В интервальном ряду
- 21. расчитаем медиану в интервальном ряду По
- 22. Тогда медиана
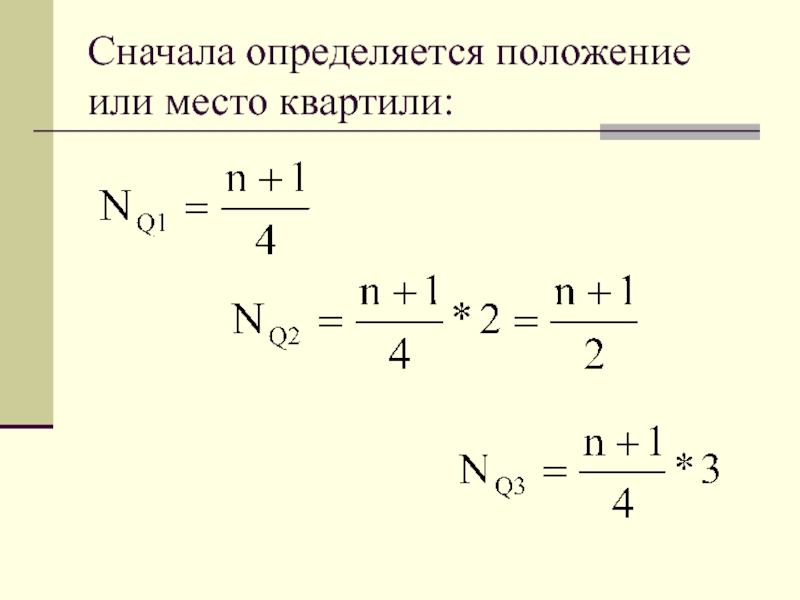
- 23. Квартиль - это значения признака, которые
- 24. Сначала определяется положение или место квартили:
- 25. В дискретном ряду по накопленным частотам
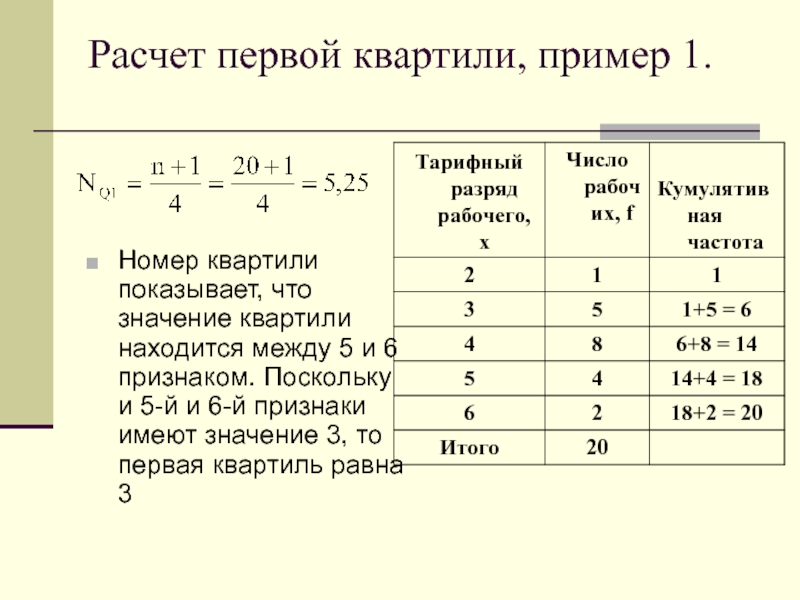
- 26. Расчет первой квартили, пример 1.
- 27. Расчет первой квартили в интервальном ряду (пример 2)
- 28. Расчет первой квартили в интервальном ряду (пример
- 29. Показатели вариации (колеблемости) признака. К абсолютным показателям
- 30. Размах колебаний (размах вариации) представляет собой
- 31. Точнее характеризуют вариацию признака показатели, основанные
- 32. Среднее линейное отклонение d для несгруппированных
- 33. Для n вариационного ряда:
- 34. Линейное отклонение в дискретном ряду d =
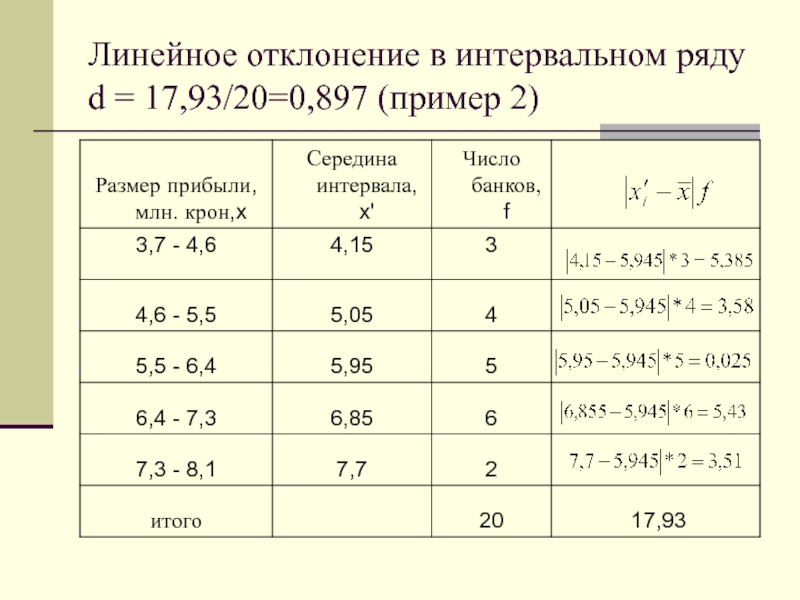
- 35. Линейное отклонение в интервальном ряду d =
- 36. Дисперсия - это средняя арифметическая квадратов
- 37. Дисперсия простая
- 38. Дисперсия взвешенная
- 39. Дисперсия в дискретном ряду
- 40. Дисперсия в интервальном ряду
- 41. Другой метод расчета дисперсии Дисперсия равна
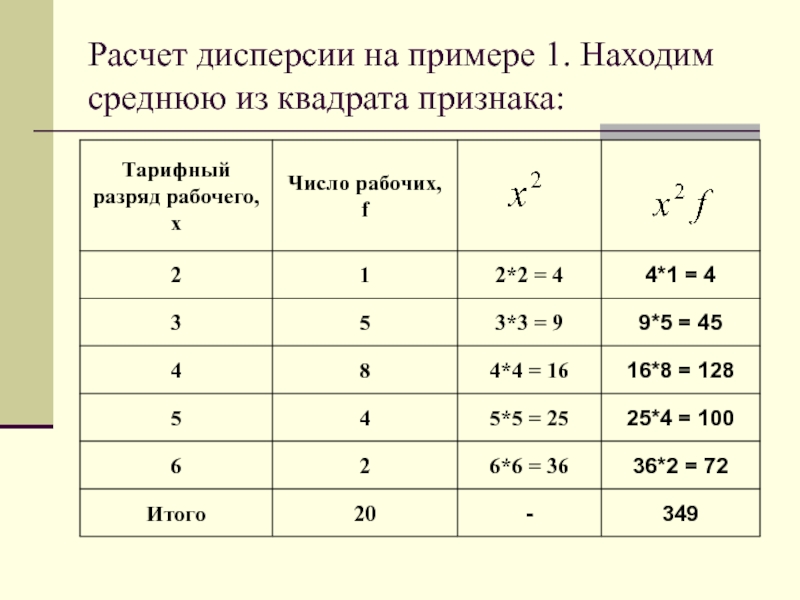
- 42. Расчет дисперсии на примере 1. Находим среднюю из квадрата признака:
- 43. Средняя из квадратов признака
- 44. Среднее квадратическое отклонение стандартное отклонение (Standard Deviation) представляет собой корень квадратный из дисперсии
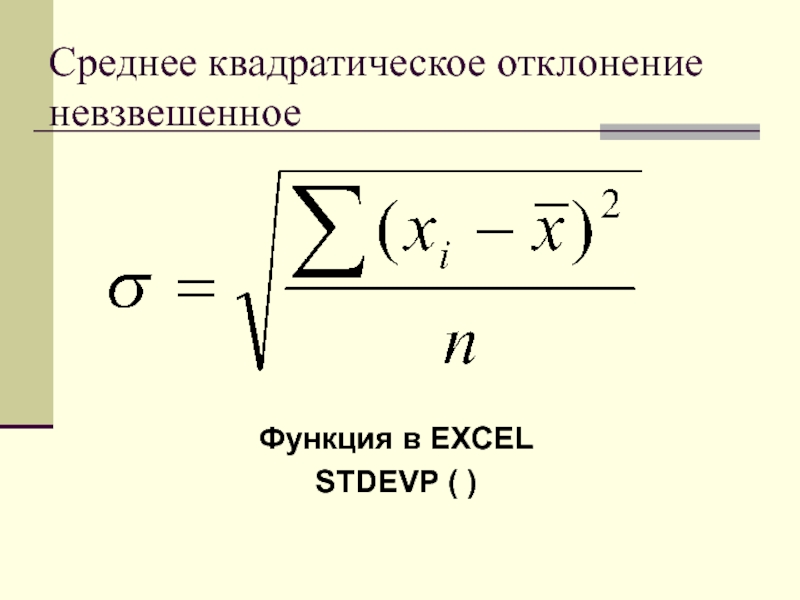
- 45. Среднее квадратическое отклонение невзвешенное
- 46. Среднее квадратическое отклонение взвешенное
- 47. Среднее квадратическое отклонение Пример 1. Пример 2.
- 48. Другие меры вариации: Относительные показатели вариации
- 49. Относительное линейное отклонение (отклонение по модулю)
- 50. Относительный показатель квартильной вариации (относительное квартильное расстояние)
- 51. Оценка степени интенсивности вариации возможна только
- 52. Моменты распределения и показатели его формы. Центральные
- 53.
- 54.
- 55. Показатели асимметрии На основе момента третьего порядка
- 56. Если А > 0, то асимметрия
- 57. Характеристика эксцесса распределения В
- 58. По значению показателей асимметрии и эксцесса
- 59. Средние квадратические отклонения ассиметрии и эксцесса
- 60. Оценка диапазона изменения статистической переменной По теореме
- 61. “ правило трех сигм”: справедливо для нормального
- 62. Закон (правило) сложения дисперсий.
- 63. Межгрупповая дисперсия
- 64. Средняя внутригрупповая дисперсия
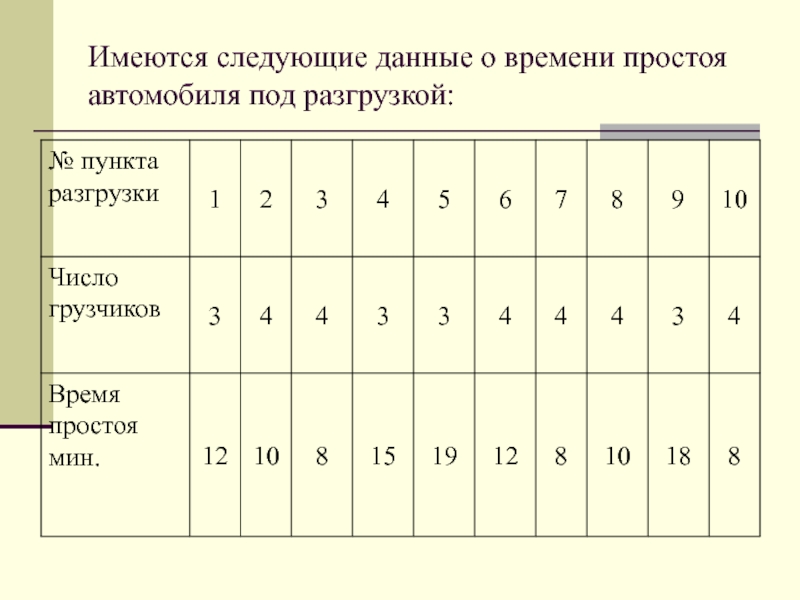
- 65. Имеются следующие данные о времени простоя автомобиля под разгрузкой:
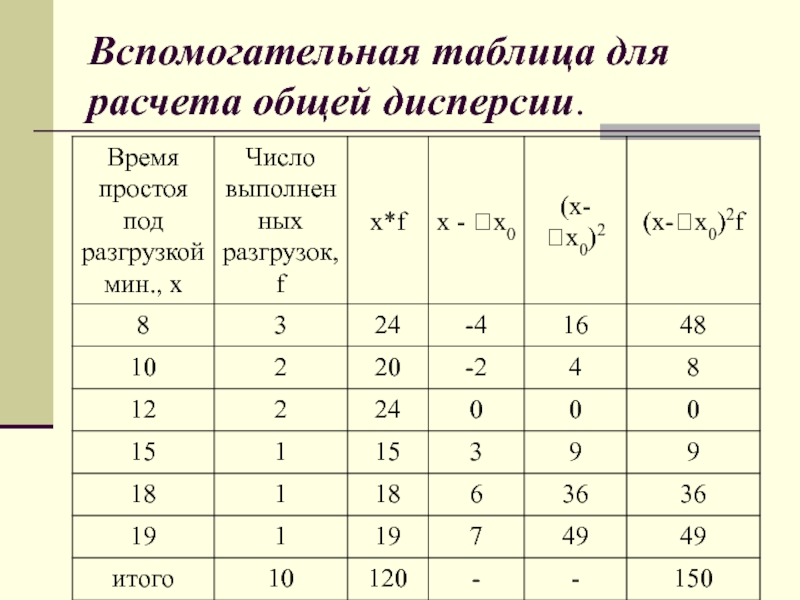
- 66. Вспомогательная таблица для расчета общей дисперсии.
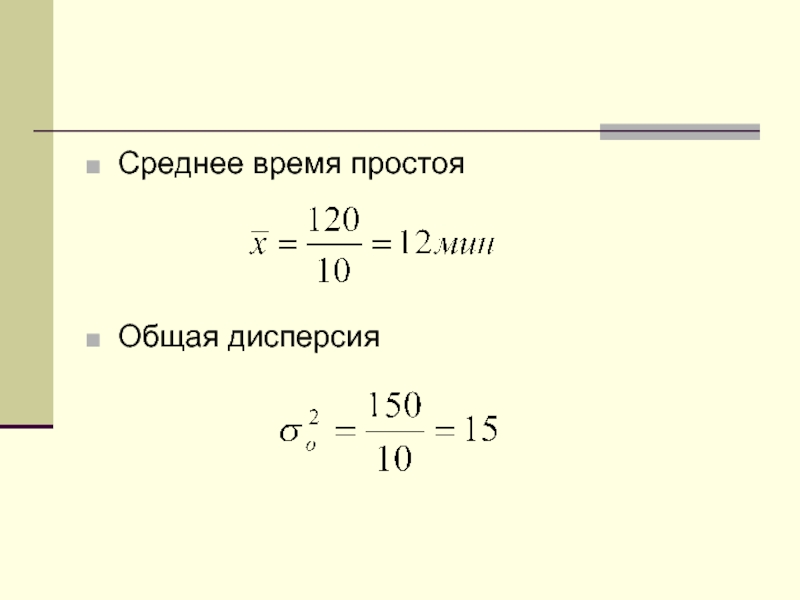
- 67. Среднее время простоя Общая дисперсия
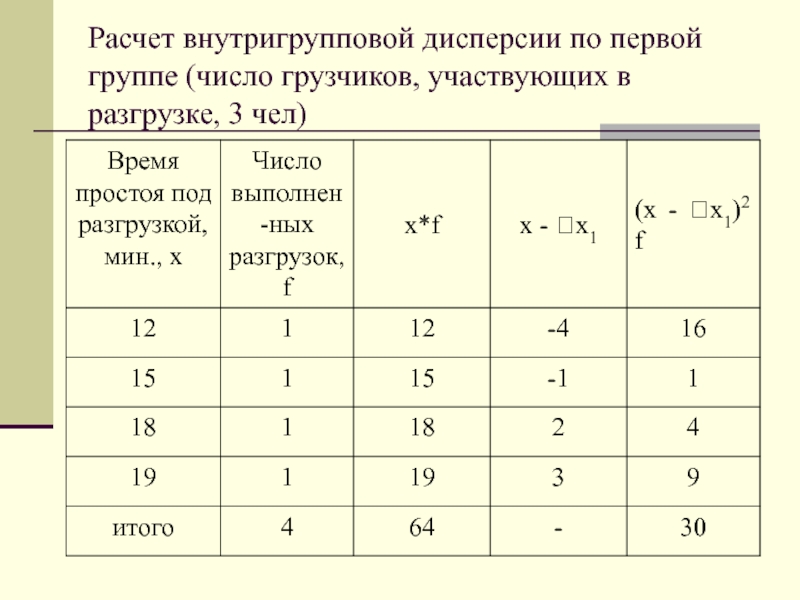
- 68. Расчет внутригрупповой дисперсии по первой группе (число грузчиков, участвующих в разгрузке, 3 чел)
- 69. Дисперсия первой группы
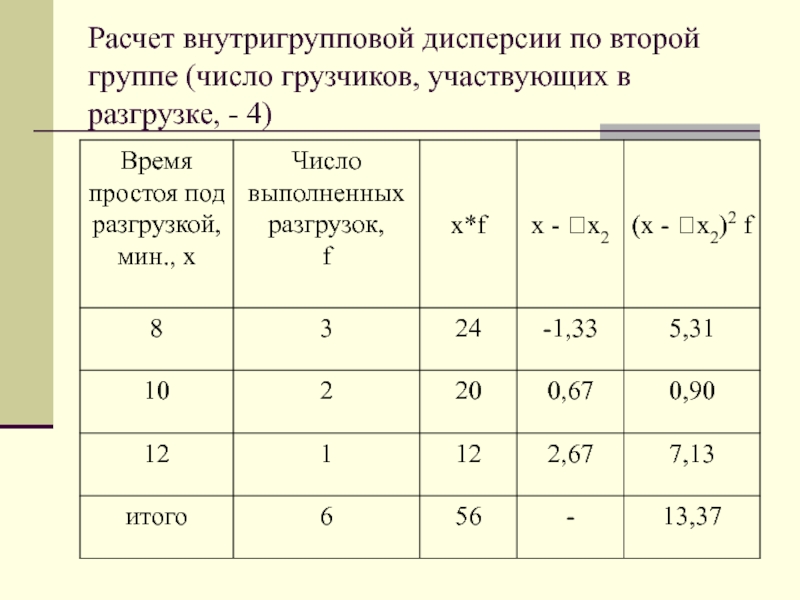
- 70. Расчет внутригрупповой дисперсии по второй группе (число грузчиков, участвующих в разгрузке, - 4)
- 71. Дисперсия второй группы
- 72. Средняя из внутригрупповых дисперсий
- 73. Межгрупповая дисперсия
- 74. Общая дисперсия
- 75. Пример 3. Расчет средней производительности труда рабочими
- 76. Среднее линейное отклонение d = 48/50 = 0,96
- 77. Дисперсия производительности труда = 74/50 =1,48
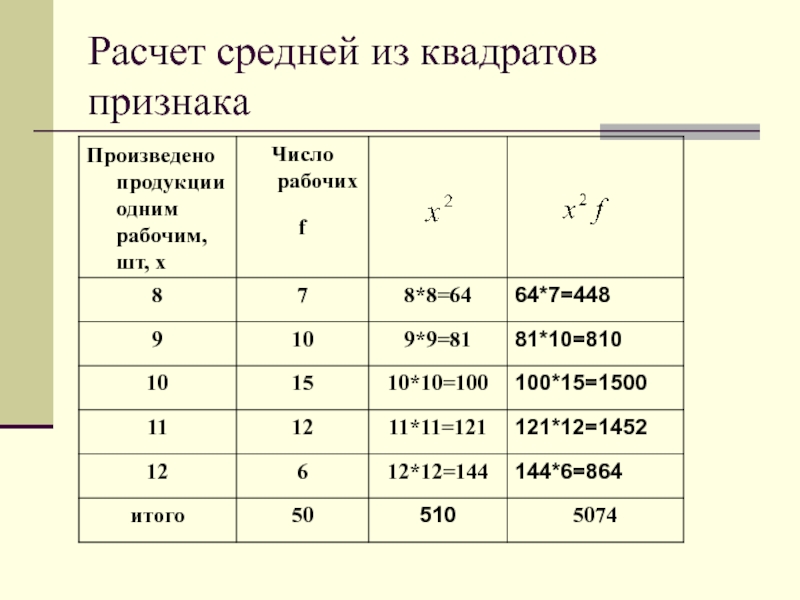
- 78. Расчет средней из квадратов признака
- 79. Средняя из квадратов признака Квадрат средней величины дисперсия
- 80. Среднее квадратическое отклонение будет равно
Слайд 2Различия индивидуальных значений признака у единиц совокупности называются вариацией признака.
Она
Слайд 3
Вариация, которая не зависит от факторов, положенных в основу выделения групп,
Слайд 4Изучение вариации в пределах одной группы предполагает использование следующих приемов:
построение вариационного
графическое изображение;
исчисление основных характеристик распределения: показателей центра распределения; показателей вариации; показателей формы распределения.
Слайд 5Вариационный ряд -
групповая таблица, построенная по количественному признаку, в сказуемом которой
Форма построения вариационного ряда зависит от характера изменения изучаемого признака.
Он может быть построен в форме дискретного ряда или в форме интервального ряда.
Слайд 7Частость расчитывается по формуле
Замена частот частостями позволяет сопоставить вариационные ряды
Слайд 9Для признака, имеющего непрерывное изменение строится интервальный вариационный ряд распределения.
Определение величины
Слайд 10Показатели центра распределения.
Средняя арифметическая для дискретного ряда расчитывается по формуле средней
Слайд 11
В интервальном ряду расчет производится по этой же формуле, но в
Слайд 14Мода (Мо)
наиболее часто встречающееся значение признака.
В дискретном ряду -
В интервальном ряду сначала определяется модальный интервал, т.е. тот, который имеет наибольшую частоту, а затем расчитывают моду по формуле:
Слайд 16
В примере 1 наибольшую частоту - 8 имеет четвертый тарифный разряд,
В примере 2 модальный интервал 6,4 -7,3 так как такой уровень прибыли имеют наибольшее число банков.
Слайд 17Медиана (Ме)
соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы
где n - число единиц в совокупности.
Слайд 18Медиана в дискретном ряду
По накопленным частотам определяют ее численное значение в
Медиана тарифного разряда будет найдена следующим образом:
Слайд 19
Следовательно, среднее значение 10-го и 11-го признаков будут соответствовать медиане.
По накопленным
Слайд 20Медиана в интервальном ряду
В интервальном ряду распределения по номеру медианы указывают
Численное значение определяется по формуле:
Слайд 21расчитаем медиану в интервальном ряду
По накопленным частотам вышеприведенного примера определяем, что
5,5 - 6,4 так как номер медианы
а это значение включает кумулятивная частота 12.
Слайд 22
Тогда медиана
Таким образом, 50% банков имеют прибыль менее 6,13 млн. крон,
Слайд 23
Квартиль - это значения признака, которые делят ранжированный ряд на четыре
Таких величин будет три:
первая квартиль(Q1),
вторая квартиль (Q2),
третья квартиль (Q3).
Вторая квартиль является медианой.
Слайд 25
В дискретном ряду по накопленным частотам определяют численное значение.
В интервальном ряду
Слайд 26Расчет первой квартили, пример 1.
Номер квартили показывает, что значение квартили находится
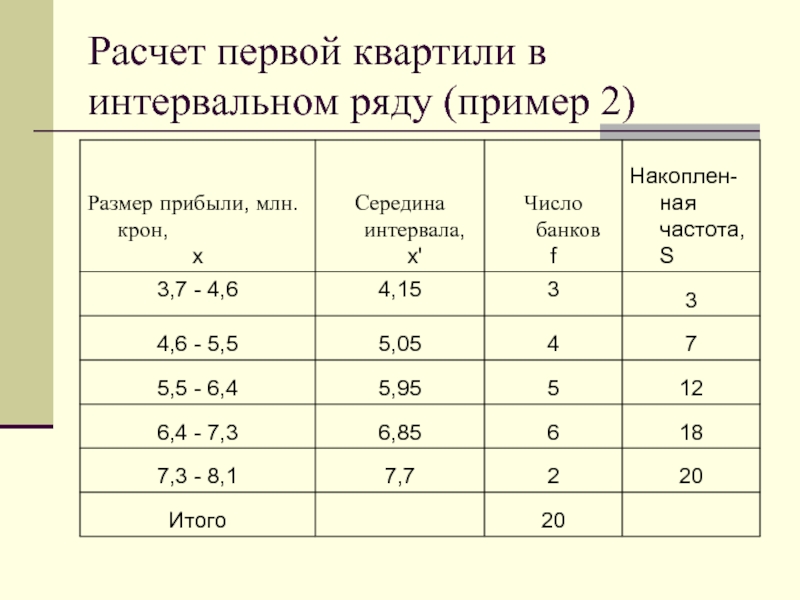
Слайд 28Расчет первой квартили в интервальном ряду (пример 2)
Расчитаем номер первой квартили
Значение
Слайд 29Показатели вариации (колеблемости) признака.
К абсолютным показателям относят:
Размах колебаний;
Среднее линейное отклонение;
Дисперсию;
Среднее квадратическое
Квартильное отклонение.
Слайд 30Размах колебаний (размах вариации)
представляет собой разность между максимальным и минимальным
Размах вариации зависит только от крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями.
Слайд 31
Точнее характеризуют вариацию признака показатели, основанные на учете колеблемости всех значений
К таким показателям относят:
среднее линейное отклонение,
дисперсию,
среднее квадратическое отклонение.
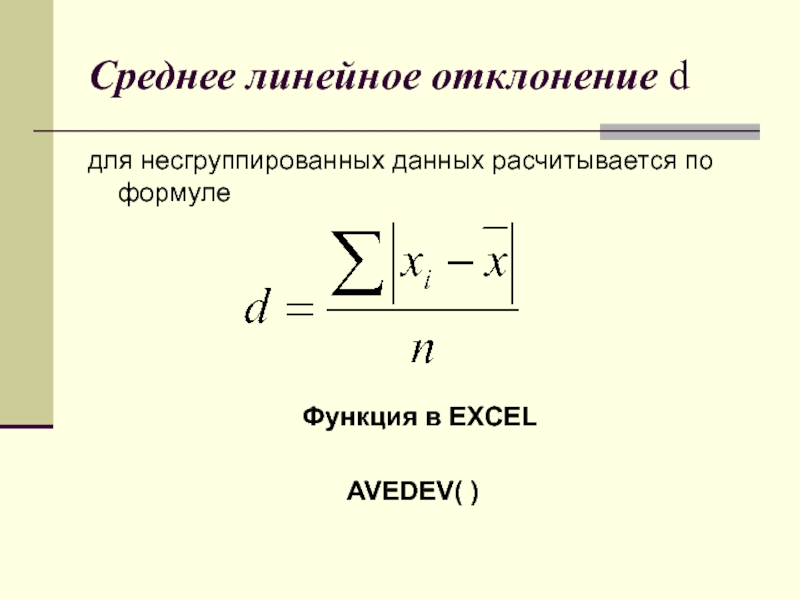
Слайд 32Среднее линейное отклонение d
для несгруппированных данных расчитывается по формуле
Функция
AVEDEV( )
Слайд 36Дисперсия
- это средняя арифметическая квадратов отклонений каждого значения признака от
Дисперсия обычно называется средним квадратом отклоненй.
В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
Слайд 41
Другой метод расчета дисперсии
Дисперсия равна разности средней из квадратов признака и
Слайд 44Среднее квадратическое отклонение
стандартное отклонение (Standard Deviation)
представляет собой корень квадратный из
Слайд 48Другие меры вариации: Относительные показатели вариации
Применяются для оценки интенсивности вариации и
относительный размах вариации (коэффициент осцилляции)
Слайд 51
Оценка степени интенсивности вариации возможна только для каждого отдельного признака и
Предположим вариация производительности труда на предприятиях Эстонии v < 10% рассматривается как слабая,10% < v < 25% -умеренная, сильная при v > 25%.
Однако, если рассматривается вариация роста взрослых людей, то при v = 4% следует говорить об очень сильной интенсивности
Слайд 52Моменты распределения и показатели его формы.
Центральные моменты распределения порядка – это
Момент первого порядка равен нулю.
Второй центральный момент представляет собой дисперсию.
Третий момент используется для оценки асимметрии
Четвертый – для оценки эксцесса.
Слайд 55Показатели асимметрии
На основе момента третьего порядка можно построить коэффициент асимметрии
или показатель Пирсона
Слайд 56
Если А > 0, то асимметрия правосторонняя, а если А
В EXCEL используется функция
SKEW ( ).
Слайд 57Характеристика эксцесса распределения
В нормальном распределении Е = 0, поэтому, если Е
Е < 0, эксцесс ниже нормального (плосковершинная кривая).
В EXCEL используется функция
KURT ( ).
Слайд 58
По значению показателей асимметрии и эксцесса можно судить о близости распределения
Если и
то распределение можно считать нормальным
Слайд 60Оценка диапазона изменения статистической переменной
По теореме Чебышева:
в интервале (μ - 2σ,
в интервале (μ - 3σ, μ +3σ) находится 89 % значений.
Слайд 61“ правило трех сигм”:
справедливо для нормального распределения
в интервале (μ - σ,
в интервале (μ - 2σ, μ +2σ) находится 95.4% значений,
в интервале (μ - 3σ, μ +3σ) находится 99.7% значений.
Слайд 62Закон (правило) сложения дисперсий.
- величина общей
- межгрупповая дисперсия
- средняя внутригрупповая дисперсия
Слайд 68Расчет внутригрупповой дисперсии по первой группе (число грузчиков, участвующих в разгрузке,
Слайд 70Расчет внутригрупповой дисперсии по второй группе (число грузчиков, участвующих в разгрузке,
Слайд 75Пример 3. Расчет средней производительности труда рабочими предприятия
Средняя производительность труда составила
Слайд 80Среднее квадратическое отклонение будет равно
Это означает, что отклонение от средней производительности