- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Средние величины. Анализ вариационных рядов. Оценка достоверности различий средних и относительных величин презентация
Содержание
- 1. Средние величины. Анализ вариационных рядов. Оценка достоверности различий средних и относительных величин
- 2. Вариационные ряды Вариационный ряд – ряд, в
- 3. Виды вариационных рядов простой – когда каждая
- 4. Примеры вариационных рядов Простой: Значения артериального давления
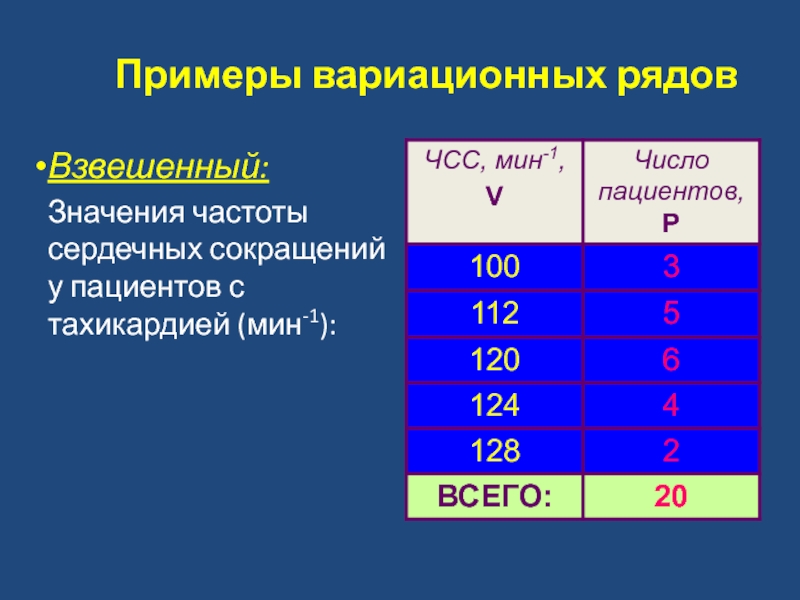
- 5. Примеры вариационных рядов Взвешенный: Значения частоты сердечных сокращений у пациентов с тахикардией (мин-1):
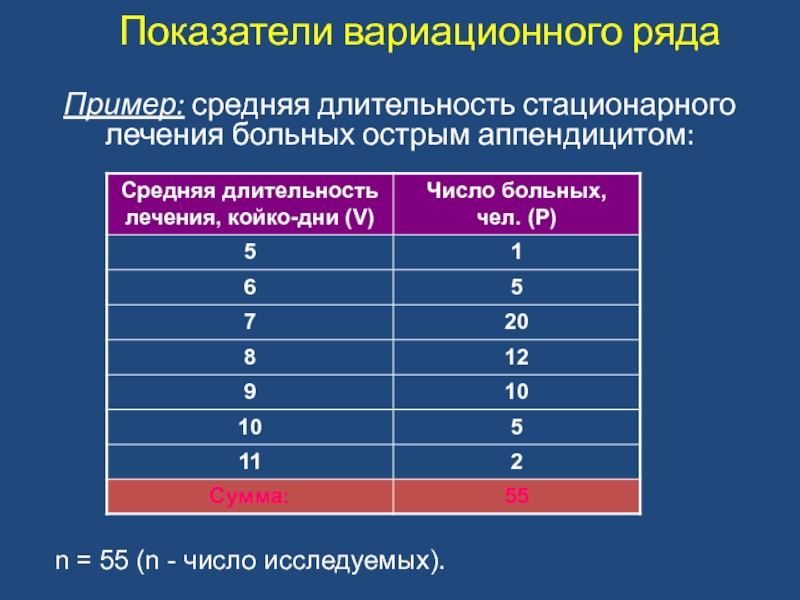
- 6. Показатели вариационного ряда Пример: средняя длительность стационарного
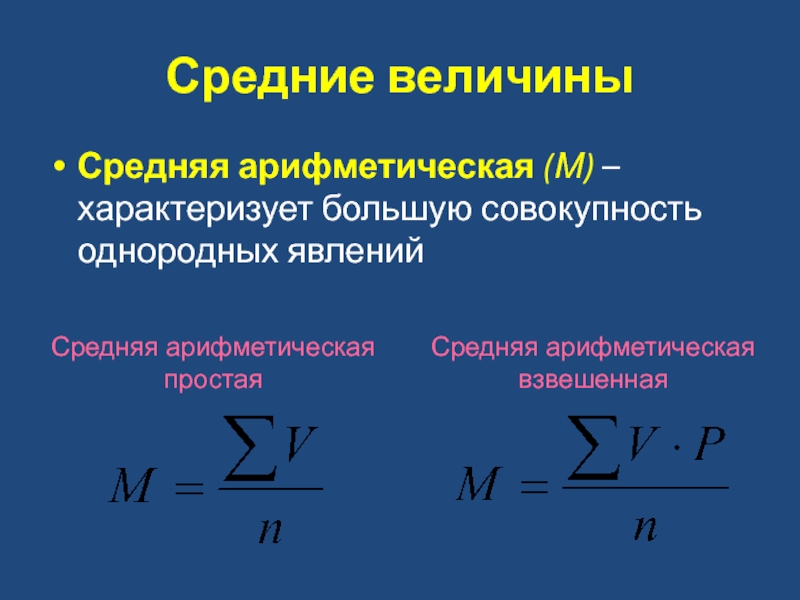
- 7. Средние величины Средняя арифметическая (М) – характеризует
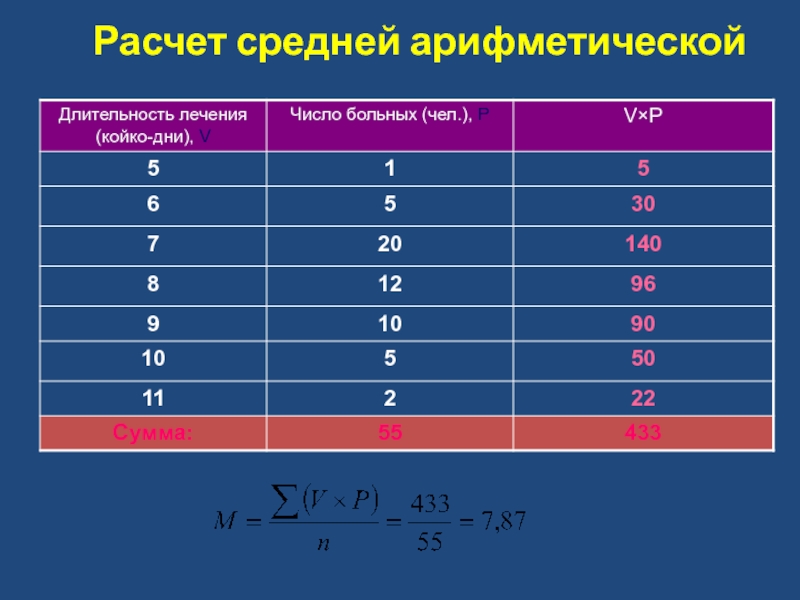
- 8. Расчет средней арифметической
- 9. Средние величины Мода (Мо) – наиболее часто
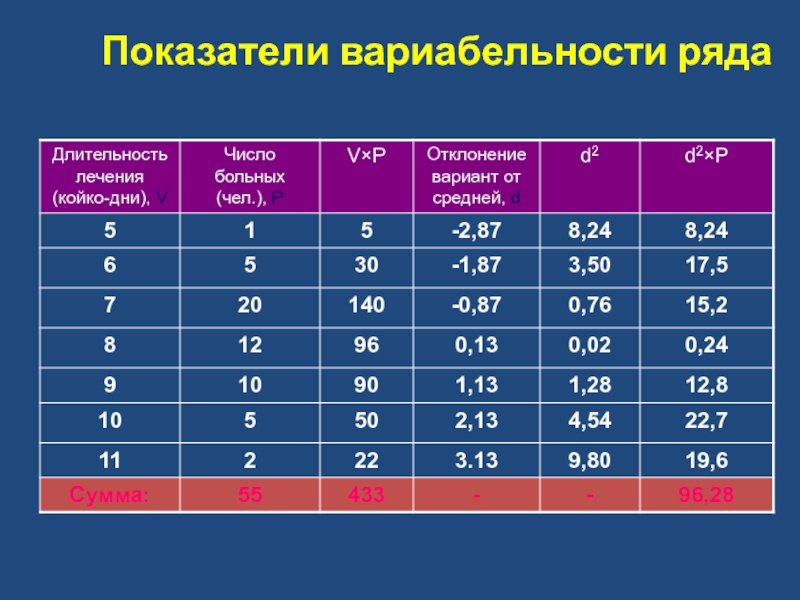
- 10. Показатели вариабельности ряда
- 11. Показатели вариабельности ряда Среднее квадратическое отклонение (сигмальное
- 12. Показатели вариабельности ряда Коэффициент вариации – определяет
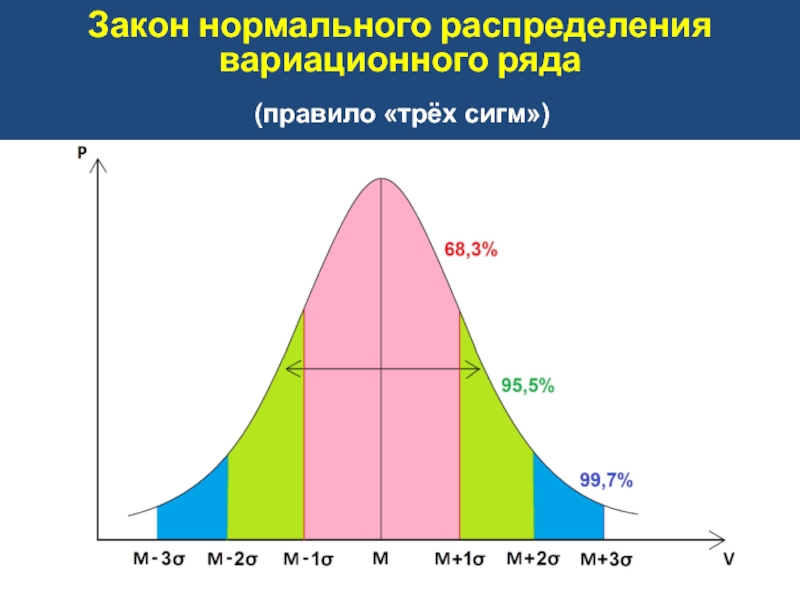
- 13. Закон нормального распределения вариационного ряда (правило «трёх сигм»)
- 14. Средняя ошибка средней арифметической Случайные ошибки репрезентативности
- 15. Средняя ошибка средней арифметической
- 16. Оценка достоверности различий средних величин Пример:
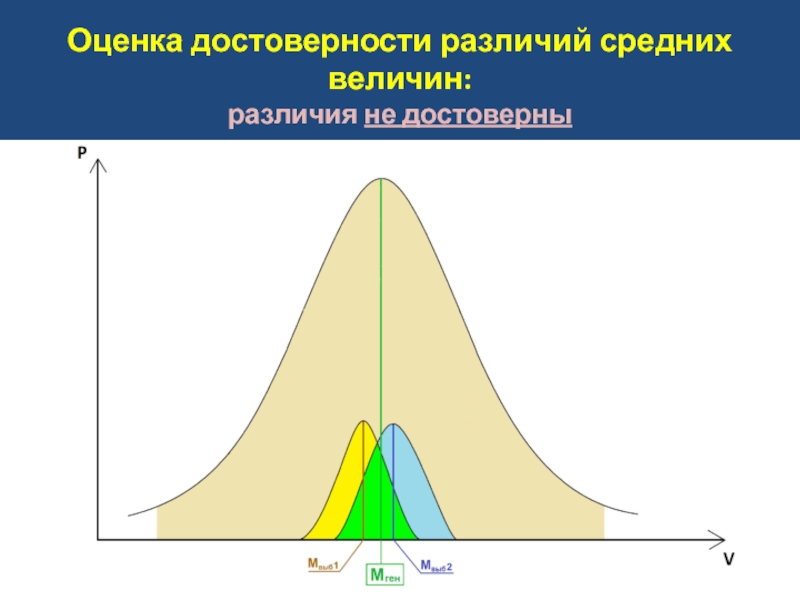
- 17. Оценка достоверности различий средних величин: различия не достоверны
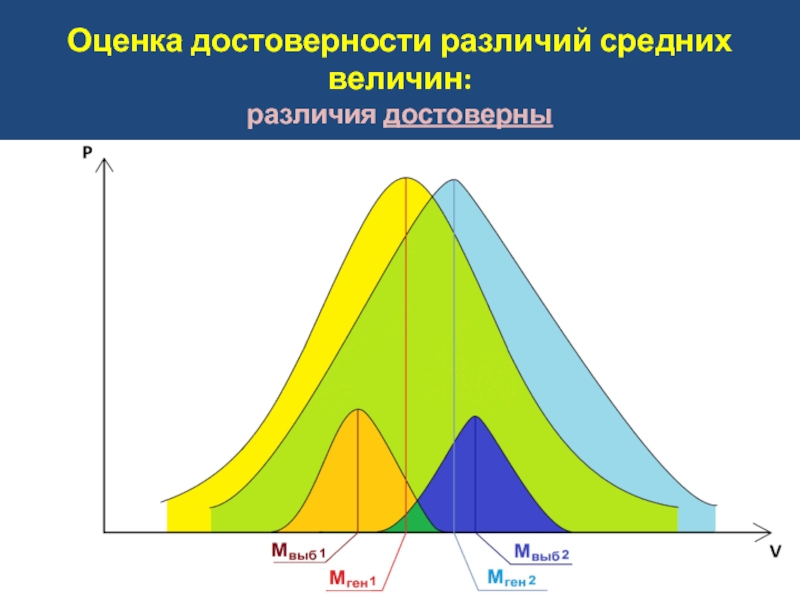
- 18. Оценка достоверности различий средних величин: различия достоверны
- 19. t-критерий Стьюдента Пример: t < 2 →
- 20. Оценка достоверности различий средних величин: различия
- 21. Оценка достоверности различий средних величин: различия
- 22. Парный t-критерий Стьюдента Используется в случае сравнения
- 23. Условия применения t-критерия Стьюдента 1) Сравниваемые выборки
- 24. Примеры ошибочных формулировок Подсчет среднего количества М
Слайд 1Средние величины. Анализ вариационных рядов. Оценка достоверности различий средних и относительных
Слайд 2Вариационные ряды
Вариационный ряд – ряд, в котором сопоставлены (по степени возрастания
Варианты (V) – отдельные количественные выражения признака
Частоты (P) – числа, показывающие, сколько раз повторяются варианты
Слайд 3Виды вариационных рядов
простой – когда каждая варианта встречается только один раз.
Математически:
взвешенный – когда одна или несколько вариант повторяются.
В данном случае значения одной или нескольких частот – более 1.
Слайд 4Примеры вариационных рядов
Простой:
Значения артериального давления у 10 обследованных пациентов (мм рт.ст.):
160;
Длительность амбулаторного приема у врача-хирурга (мин):
10; 12; 15; 16; 18; 20; 25; 30
Слайд 5Примеры вариационных рядов
Взвешенный:
Значения частоты сердечных сокращений у пациентов с тахикардией (мин-1):
Слайд 6Показатели вариационного ряда
Пример: средняя длительность стационарного лечения больных острым аппендицитом:
n =
Слайд 7Средние величины
Средняя арифметическая (М) – характеризует большую совокупность однородных явлений
Средняя
Средняя арифметическая взвешенная
Слайд 9Средние величины
Мода (Мо) – наиболее часто повторяющаяся варианта
Пример: Мо = 7,
Медиана (Ме) – значение варианты, делящей вариационный ряд пополам: по обе стороны от нее находится равное число вариант
Пример: Ме = V28 = 8
Слайд 11Показатели вариабельности ряда
Среднее квадратическое отклонение (сигмальное отклонение, сигма) – определяет степень
Если n ≤ 30
Если n > 30
Пример:
Слайд 12Показатели вариабельности ряда
Коэффициент вариации – определяет степень колеблемости вариационного ряда
Критерии значений
<10% - слабая колеблемость
10-20% - средняя колеблемость
>20% - сильная колеблемость
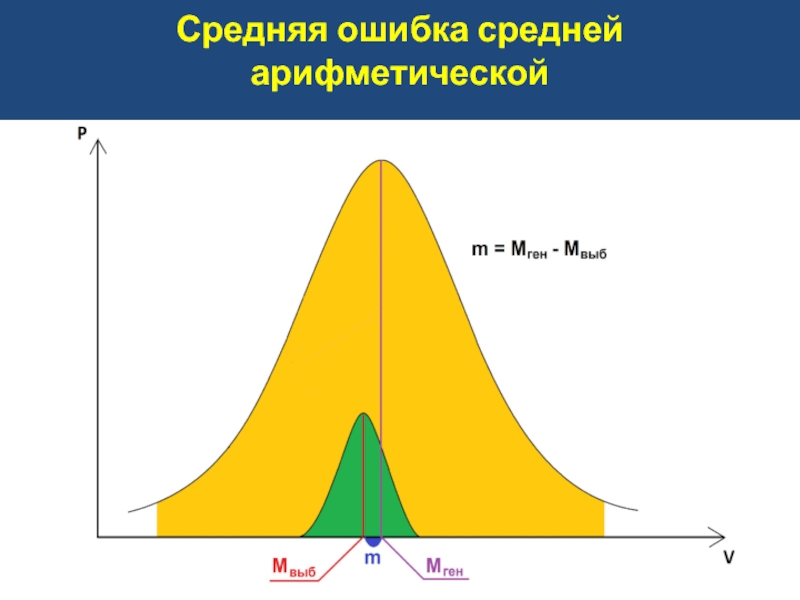
Слайд 14Средняя ошибка средней арифметической
Случайные ошибки репрезентативности – разность между средними или
Средняя ошибка средней арифметической (m):
Если n ≤ 30
Если n > 30
Пример:
Слайд 16Оценка достоверности различий средних величин
Пример:
Средняя длительность стационарного лечения больных острым
Средняя длительность стационарного лечения больных острым аппендицитом, прооперированных лапароскопическим методом, составила 6,85±0,23 койко-дней.
Вопрос: Достоверно ли сокращение длительности стационарного лечения больных острым аппендицитом, прооперированных лапароскопическим методом по сравнению с контрольной группой?
Слайд 19t-критерий Стьюдента
Пример:
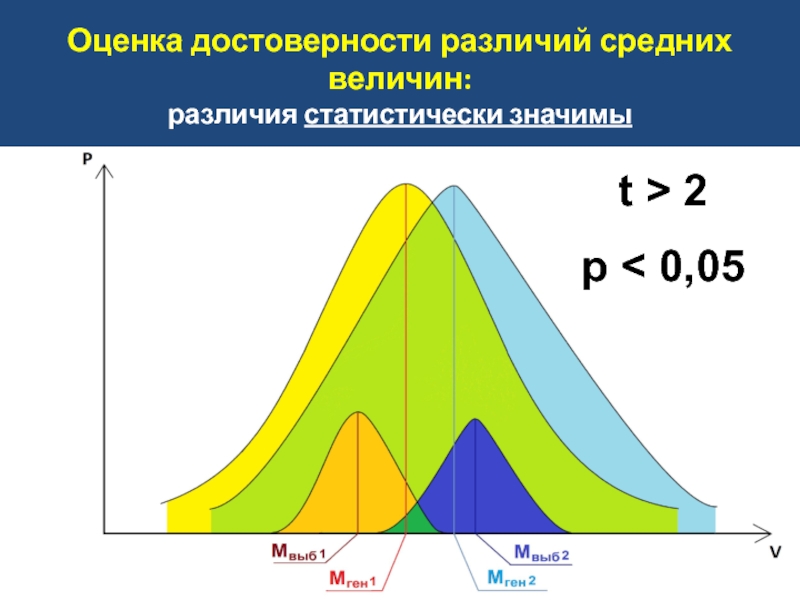
t < 2 → p > 0,05 – различия статистически
t > 2 → p < 0,05 – различия статистически значимы
p – уровень значимости (вероятность ошибки) – вероятность того, что две выборочные совокупности принадлежат одной генеральной совокупности, или вероятность того, что мы сочли различия существенными, а они на самом деле случайны
Разработан английским химиком У.Госсетом, (1908г., публикация в журнале «Биометрика» под псевдонимом «Student»)
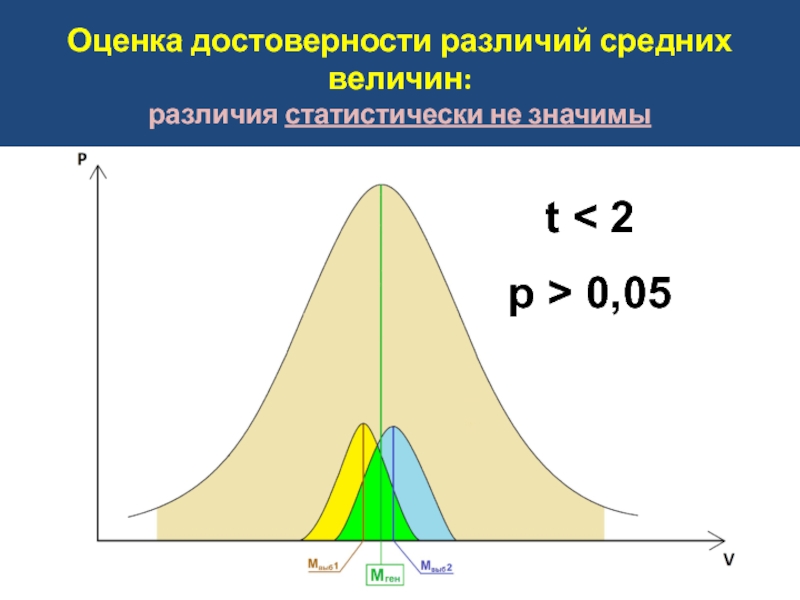
Слайд 20Оценка достоверности различий средних величин:
различия статистически не значимы
t < 2
р
Слайд 22Парный t-критерий Стьюдента
Используется в случае сравнения результатов измерений в одной и
где: Md – средняя арифметическая изменений показателя для каждого исследуемого (d),
m – ее средняя ошибка (вычисляется по обычной формуле)
Слайд 23Условия применения t-критерия Стьюдента
1) Сравниваемые выборки должны соответствовать закону нормального распределения:
соблюдается «правило трех сигм»
2) Дисперсии сравниваемых выборок – одинаковы (гомоскедастичны).
Это условие проверяется с помощью специальных статистических тестов.
Слайд 24Примеры ошибочных формулировок
Подсчет среднего количества М ± m производили по методу
Статистическую обработку данных производили по методу Стьюдента с применением критерия хи-квадрат.
Результаты обрабатывали статистически с определением средней арифметической, стандартной ошибки и доверительного интервала при Р > 0,05.
Корреляционный анализ проводили путем сравнения двух групп с помощью критерия t.
Материал обрабатывали статистически по методу Кучеренко.
Достоверность значений определяли по t-критерию Стьюдента
Статистическая обработка материала произведена с использованием мини-ЭВМ "Искра-1256" по стандартным программам.