- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Современные системы компьютерной математики презентация
Содержание
- 1. Современные системы компьютерной математики
- 2. Бесплатный аналог MathCad Веб-сервис http://smath.info/cloud/
- 3. Тема 1. Задачи элементарной математики
- 4. Работа с числовыми выражениями Активные панели для работы с числовыми выражениями Вид → Панели инструментов
- 5. Особенности работы с MathCad В процессе вычисления
- 6. Операторы преобразования Для буквенных выражений необходимо использовать ключевые слова – операторы преобразования
- 7. Особенности работы с MathCad Панель «Калькулятор» содержит
- 8. Решение уравнений и неравенств Решение уравнений и
- 9. Тема 2 Функции и их графики Элементарные графики функций
- 10. Активные панели Для работы с функциями и
- 11. Функции MathCad позволяет работать функциями, заданными аналитически,
- 12. Функции Для определения функции на заданном отрезке
- 13. Графики Нажмите кнопку График X-Y на панели
- 14. Графики Если необходимо построить в одной системе
- 15. Графики Для построения графика функции, заданной кусочно,
- 16. Тема 2 Функции и их графики Графики параметрических функций Трехмерные графики
- 17. Графики параметрических функций Функция y =
- 18. Графики параметрических функций Постройте график параметрической
- 19. Трехмерные графики Для построения трехмерных графиков используется
- 20. Трехмерные графики Постройте графики эллиптического параболоида f=x2 +y2 Форматируйте трехмерный график как на рисунке
- 21. Тема 3. Решение уравнений
- 22. Графическое решение уравнений Уравнение можно рассматривать
- 23. Графическое решение уравнений Перемещайте появившиеся пунктирные
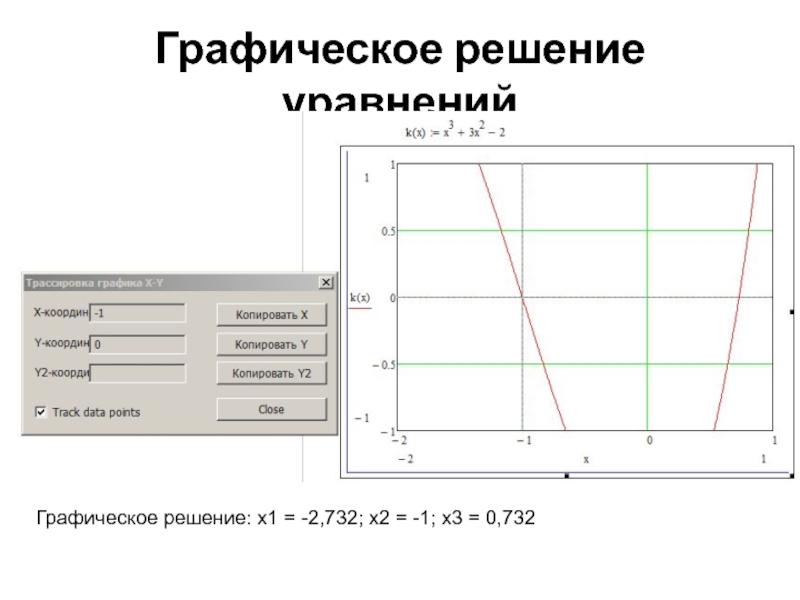
- 24. Графическое решение уравнений Графическое решение: х1 = -2,732; х2 = -1; х3 = 0,732
- 25. Решение уравнений операцией solve Ввести левую часть
- 26. Решение уравнений операцией solve
- 27. Решение систем уравнений Введите слово Given (Дано)
- 28. Решение систем уравнений
- 29. Тема 4. Типовые задачи математического анализа
- 30. Вычисление суммы значений функции Для решения задач
- 31. Вычисление суммы значений функции Существует два способа
- 32. Вычисление пределов Чтобы вычислить предел, надо записать
- 33. Вычисление производных с помощью шаблона панели
- 34. Вычисление производных MathCad не упрощает выражений,
- 35. Вычисление интегралов с помощью шаблона панели
- 36. Вычисление интегралов с помощью шаблона панели
- 37. Операции с матрицами Панель Вектор и
Бесплатный аналог MathCad Веб-сервис http://smath.info/cloud/
Слайд 4Работа с числовыми выражениями
Активные панели для работы с числовыми выражениями
Вид →
Панели инструментов
Слайд 5Особенности работы с MathCad
В процессе вычисления значений числовых выражений следует различать
знаки
Рассчитать численно (=)
Аналитические преобразования (→)
Рассчитать численно (=)
Аналитические преобразования (→)
ПРОВЕРИТЬ!
Слайд 6Операторы преобразования
Для буквенных выражений необходимо использовать ключевые слова – операторы преобразования
Слайд 7Особенности работы с MathCad
Панель «Калькулятор» содержит кнопки вызова трёх тригонометрических функций
–sin, cos и tan.
Для вызова других функций необходимо на панели инструментов щёлкнуть по кнопке f(x) («вставить функцию»), в открывшемся диалоговом окне выбрать категорию функции «Тригонометрические» и найти имя подходящей функции
Для вызова других функций необходимо на панели инструментов щёлкнуть по кнопке f(x) («вставить функцию»), в открывшемся диалоговом окне выбрать категорию функции «Тригонометрические» и найти имя подходящей функции
Слайд 8Решение уравнений и неравенств
Решение уравнений и неравенств выполняется, одной строкой, с
использованием ключевого слова «solve» («решить»)
Слайд 10Активные панели
Для работы с функциями и их графиками в основном используются
панели «Калькулятор» и «График»
Слайд 11Функции
MathCad позволяет работать функциями, заданными аналитически, а также с их отдельными
значениями
Для определения функции вместо знака «равно» (=) используется знак «присвоить» (:=)
f(x):=x2
Чтобы вычислить значения функции в заданных точках, надо ввести значение аргумента вместо переменной и выбрать знак «равно» (=)
Для определения функции вместо знака «равно» (=) используется знак «присвоить» (:=)
f(x):=x2
Чтобы вычислить значения функции в заданных точках, надо ввести значение аргумента вместо переменной и выбрать знак «равно» (=)
Слайд 12Функции
Для определения функции на заданном отрезке
f(x):=x2 х∈[–2; 1]
Используется ранжированная переменная
x:=-2,-1.5..1
Чтобы
задать промежуток значений аргумента [–2; 1] с шагом 0,5 необходимо при латинской раскладке клавиатуры ввести следующий набор символов: х, знак «:=», –2, запятая, –1, точка, 5, двоеточие (автоматически превращается в «..»), 1
Слайд 13Графики
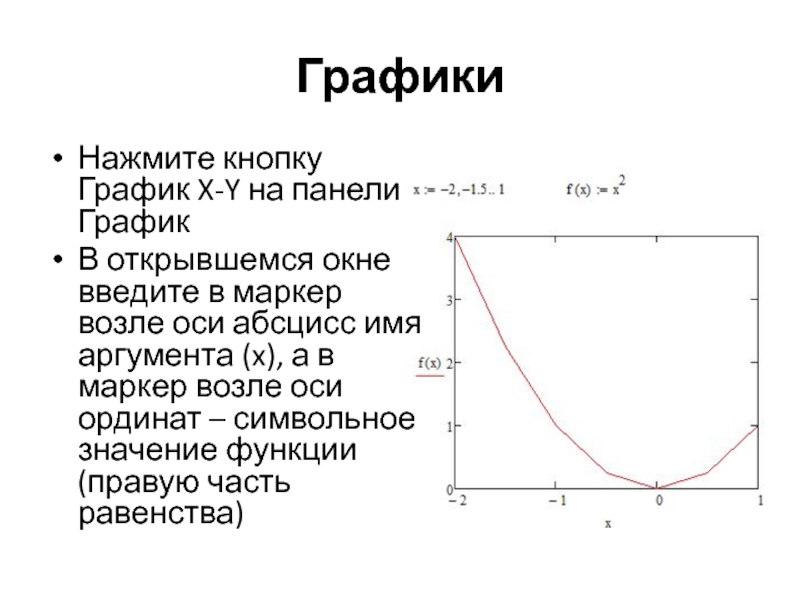
Нажмите кнопку График X-Y на панели График
В открывшемся окне введите
в маркер возле оси абсцисс имя аргумента (x), а в маркер возле оси ординат – символьное значение функции (правую часть равенства)
Слайд 14Графики
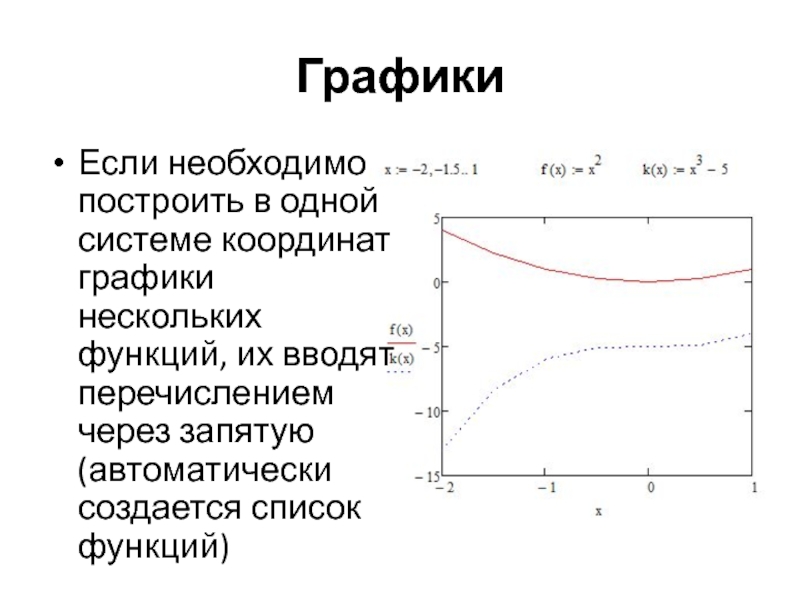
Если необходимо построить в одной системе координат графики нескольких функций, их
вводят перечислением через запятую (автоматически создается список функций)
Слайд 15Графики
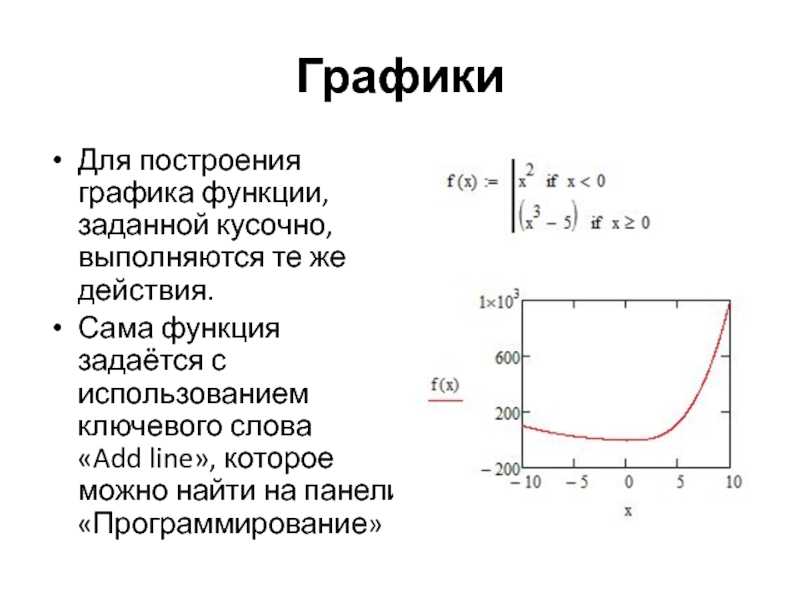
Для построения графика функции, заданной кусочно, выполняются те же действия.
Сама
функция задаётся с использованием ключевого слова
«Add line», которое можно найти на панели «Программирование»
Слайд 17Графики параметрических функций
Функция y = y(x), называется параметрической, если координаты
каждой точки (x; y) которой вычислены как функции параметра t:
(x; y) =( x(t), y(t) )
Для построения графика выполните следующее:
Задайте параметрическую функцию
Воспользуйтесь панелью инструментов График, и в открывшемся окне введите в маркер возле оси абсцисс имя аргумента x(t), а в маркер возле оси ординат y(t).
Установите по осям требуемые интервалы отображения
Для построения графика выполните следующее:
Задайте параметрическую функцию
Воспользуйтесь панелью инструментов График, и в открывшемся окне введите в маркер возле оси абсцисс имя аргумента x(t), а в маркер возле оси ординат y(t).
Установите по осям требуемые интервалы отображения
Слайд 18Графики параметрических функций
Постройте график параметрической функции:
Установите по оси ОХ интервал
от 0 до 1,5
Установите по оси ОУ интервал от -10 до 10
Установите по оси ОУ интервал от -10 до 10
Слайд 19Трехмерные графики
Для построения трехмерных графиков используется кнопка График поверхностей на панели
График
Для построения графика поверхности выполните следующее:
Задайте функцию и создайте окно для построения
В маркер в нижнем левом углу окна введите «f» и щёлкните вне поля графика
Измените вид графика (цвет, начертание линий, заливки и т.п.), щёлкнув по графику дважды.
Наведите курсор на график, зажмите ЛМ и перемещайте мышь – график будет вращаться.
Движение колёсика изменяет масштаб отображения
Для построения графика поверхности выполните следующее:
Задайте функцию и создайте окно для построения
В маркер в нижнем левом углу окна введите «f» и щёлкните вне поля графика
Измените вид графика (цвет, начертание линий, заливки и т.п.), щёлкнув по графику дважды.
Наведите курсор на график, зажмите ЛМ и перемещайте мышь – график будет вращаться.
Движение колёсика изменяет масштаб отображения
Слайд 20Трехмерные графики
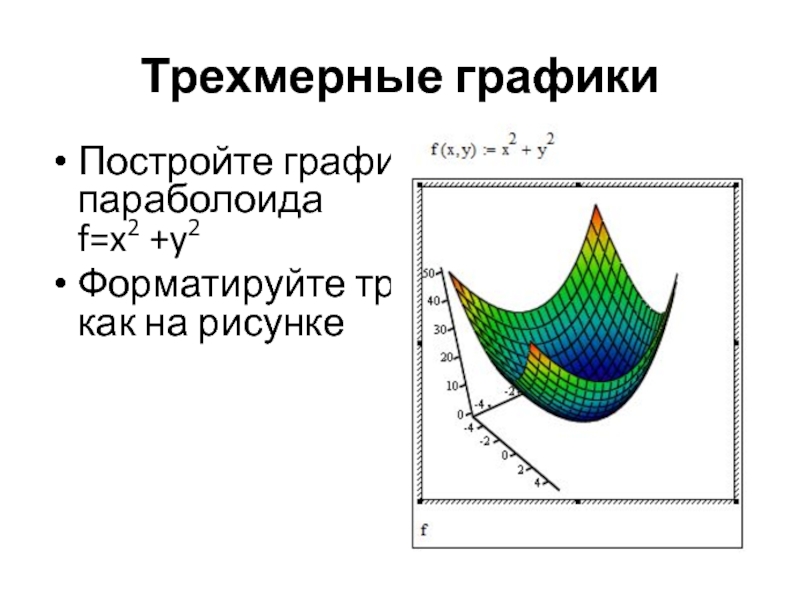
Постройте графики эллиптического параболоида
f=x2 +y2
Форматируйте трехмерный график как на
рисунке
Слайд 22Графическое решение уравнений
Уравнение можно рассматривать как функцию от х.
Необходимо
найти значения аргумента х, при которых функция принимает нулевое значение
Следует задать функцию и построить ее график
Выполнить трассировку: Формат → Графики → Трассировка
Следует задать функцию и построить ее график
Выполнить трассировку: Формат → Графики → Трассировка
Слайд 23Графическое решение уравнений
Перемещайте появившиеся пунктирные линии по графику
В окне
X-Y Trace отображаются соответственные значения x и y
Найдите такое положение линий, при котором у = 0, и посмотрите, какое значение х ему соответствует
Это и есть решение данного уравнения. Решений может быть несколько!
Найдите такое положение линий, при котором у = 0, и посмотрите, какое значение х ему соответствует
Это и есть решение данного уравнения. Решений может быть несколько!
Слайд 25Решение уравнений операцией solve
Ввести левую часть уравнения, предварительно приведя его к
виду f(x)=0;
На панели Математика щёлкнуть кнопку Символьные
На панели Символьные выбрать Solve (Решить), а в маркер впечатать имя переменной
Щелкнуть вне рамки уравнения
На панели Математика щёлкнуть кнопку Символьные
На панели Символьные выбрать Solve (Решить), а в маркер впечатать имя переменной
Щелкнуть вне рамки уравнения
Слайд 27Решение систем уравнений
Введите слово Given (Дано) с клавиатуры. Оно указывает на
то, что дальше будет система уравнений. Нажмите Enter
Введите уравнения. Знак «равно» вводите, одновременно нажимая клавиши «Ctrl» + «=» или выбрав операцию Равно на палитре Булева алгебра
Выполните вставку функции Find (Найти) и перечислите имена искомых переменных
Щёлкните по стрелочке (символьному знаку равенства) на панели Символьные
Щёлкните вне рамки, появится ответ
Введите уравнения. Знак «равно» вводите, одновременно нажимая клавиши «Ctrl» + «=» или выбрав операцию Равно на палитре Булева алгебра
Выполните вставку функции Find (Найти) и перечислите имена искомых переменных
Щёлкните по стрелочке (символьному знаку равенства) на панели Символьные
Щёлкните вне рамки, появится ответ
Слайд 30Вычисление суммы значений функции
Для решения задач математического анализа используется панель инструментов
Математический анализ
Для вычисления суммы значений некоторой функции fi при целочисленном индексе i, меняющемся от начального значения n до конечного значения m, пользуются кнопкой Сумма
Для вычисления суммы значений некоторой функции fi при целочисленном индексе i, меняющемся от начального значения n до конечного значения m, пользуются кнопкой Сумма
Слайд 31Вычисление суммы значений функции
Существует два способа вычислений суммы
Численный (используется знак «=»
для нахождения результата)
Аналитический (используется знак «→» для нахождения результата)
Аналитический (используется знак «→» для нахождения результата)
Слайд 32Вычисление пределов
Чтобы вычислить предел, надо записать функцию, используя знак
глобального присвоения. Под знаком предела можно записывать либо левую, либо правую часть равенства
Слайд 33Вычисление производных
с помощью шаблона панели Математический анализ
Вычислить производную функции
Выбрать шаблон производной
Заполнить
маркеры шаблона
На панели Калькулятор нажать символический знак равенства →
На панели Калькулятор нажать символический знак равенства →
Слайд 34Вычисление производных
MathCad не упрощает выражений, поэтому они зачастую громоздки
После нахождения производных
можно попробовать упростить полученные выражения
Слайд 35Вычисление интегралов
с помощью шаблона панели Математический анализ
Если интеграл неберущийся, то программа
повторяет исходное выражение интеграла
При вычислении интегралов численными методами подынтегральную функцию необходимо максимально упростить
При вычислении интегралов численными методами подынтегральную функцию необходимо максимально упростить
Слайд 36Вычисление интегралов
с помощью шаблона панели Математический анализ
Если интеграл неберущийся, то программа
повторяет исходное выражение интеграла
При вычислении интегралов численными методами подынтегральную функцию необходимо максимально упростить
При вычислении интегралов численными методами подынтегральную функцию необходимо максимально упростить
Слайд 37Операции с матрицами
Панель Вектор и матрица
Даны две матрицы
Найти:
Сумму, разность и скалярное
произведение матриц
