- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Составляющие постановки задачи оптимизации презентация
Содержание
- 1. Составляющие постановки задачи оптимизации
- 2. Составляющие постановки задачи оптимизации Решение (план)
- 3. Формальная постановка задачи оптимизации
- 4. Краткая классификация оптимизационных задач
- 5. Задача линейного программирования (ЛП) Общая задача
- 6. Матричная форма общей задачи ЛП
- 7. В постановке (5), (6):
- 8. 2. Стандартная задача ЛП
- 9. 3. Каноническая задача ЛП
- 10. Экономические интерпретации задачи ЛП Задача планирования производства
- 11. Какое количество единиц каждого продукта необходимо произвести,
- 12. 3. Целевая функция: чистая прибыль от реализации
- 13. Формальная постановка задачи планирования производства Требуется
- 14. Транспортная задача (ТЗ)
- 15. II.1. ТЗ по критерию стоимости Предполагаем,
- 16. Емкости складов д.б. израсходованы полностью:
- 17. Формальная постановка ТЗ по критерию стоимости Требуется
- 18. II.2. ТЗ по критерию времени Предполагаем, что
- 19. 3. Общее время всех перевозок
- 20. Формальная постановка ТЗ по критерию времени Требуется
- 21. Пример 1. Сформулировать постановку задачи планирования производства
- 22. Прибыль от реализации единицы продукции
- 23. Потребление ресурсов не должно превышать их запасы:
- 24. Пример 2. Привести стандартную задачу ЛП к
- 25. Каноническая форма: при ограничениях
Слайд 1Список литературы
Исследование операций в экономике: Учебное пособие для вузов / Н.Ш.
Акулич И.Л. Математическое программирование в примерах и задачах: Учебное пособие. – М.: Высш. шк., 1993. – 336 с.
Соловьев В.И. Методы оптимальных решений: Учебное пособие. – М.: Финансовый университет, 2012. - 364 с.
Слайд 2Составляющие постановки задачи оптимизации
Решение (план) задачи - вектор
Целевая функция (функция цели, показатель эффективности) .
Условия (система ограничений), налагаемые на компоненты вектора .
Слайд 3Формальная постановка задачи оптимизации
определить
где
(2)
Допустимый план , доставляющий функции цели экстремальное значение (min или max), называется оптимальным.
Слайд 93. Каноническая задача ЛП
определить
где
(10)
!!! Замечание. Любая задача ЛП может быть представлена в виде канонической, стандартной или общей задачи ЛП.
Слайд 11Какое количество единиц каждого продукта необходимо произвести, чтобы получить максимальную прибыль?
1. План производства:
2. Ограничения.
Физический смысл:
; (11)
Условие ограниченного спроса:
; (12)
Ресурсов должно хватить:
; (13)
Слайд 123. Целевая функция: чистая прибыль от реализации всего плана производства
Себестоимость
Чистая прибыль от реализации единицы продукции :
Чистая прибыль от реализации всего плана производства:
(14)
Слайд 13Формальная постановка задачи планирования производства
Требуется определить план производства
вида (14) при соблюдении ограничений на вектор вида (11), (12), (13).
Замечание. Постановка (11)-(14) является стандартной задачей ЛП.
Слайд 15II.1. ТЗ по критерию стоимости
Предполагаем, что
-
, т.е. ТЗ с правильным балансом.
Постановка задачи.
1. План производства: .
2. Ограничения.
физический смысл:
. (15)
Слайд 16
Емкости складов д.б. израсходованы полностью:
. (16)
Заявки, поданные потребителями, д.б. удовлетворены:
. (17)
3. Общая стоимость перевозок:
. (18)
Слайд 17Формальная постановка ТЗ по критерию стоимости
Требуется определить план перевозок
вида (18) при соблюдении ограничений на вектор вида (15), (16), (17).
Замечание. Постановка (15)-(18) является канонической задачей ЛП.
Слайд 18II.2. ТЗ по критерию времени
Предполагаем, что
, т.е. ТЗ с правильным балансом.
Постановка задачи.
1. План производства: .
2. Ограничения:– (15)-(17).
Слайд 19
3. Общее время всех перевозок – все перевозки
(19)
Слайд 20Формальная постановка ТЗ по критерию времени
Требуется определить план перевозок
вида (19) при соблюдении ограничений на вектор вида (15), (16), (17).
Замечание. Постановка (15), (16), (17), (19) является задачей нелинейного программирования.
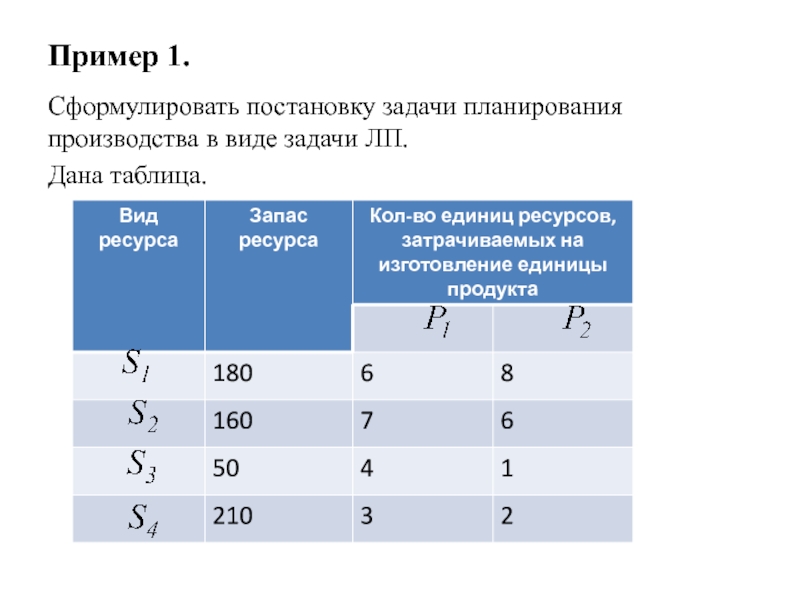
Слайд 21Пример 1.
Сформулировать постановку задачи планирования производства в виде задачи ЛП.
Дана таблица.
Слайд 22Прибыль от реализации единицы продукции и
Требуется найти план производства продукции, при котором
Прибыль от ее реализации будет максимальной.
Решение. - план производства продукции
и соответственно.
Для реализации плана производства потребуется ресурсов
: ; : ;
: ; : .
Слайд 23Потребление ресурсов не должно превышать их запасы:
Исходя из физического смысла:
(21)
Суммарная прибыль:
(22)