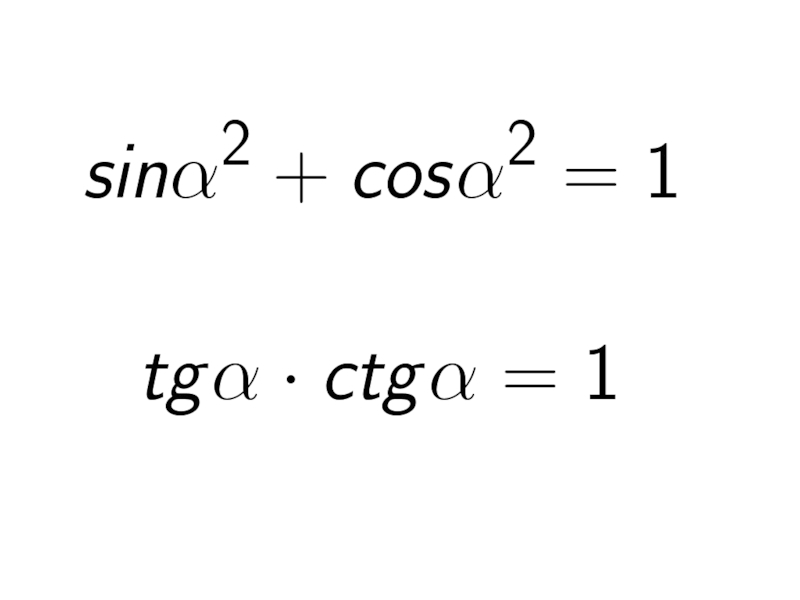- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Соотношения между сторонами и углами прямоугольного треугольника презентация
Содержание
- 1. Соотношения между сторонами и углами прямоугольного треугольника
- 2. Синус, косинус, тангенс острого угла прямоугольного треугольника
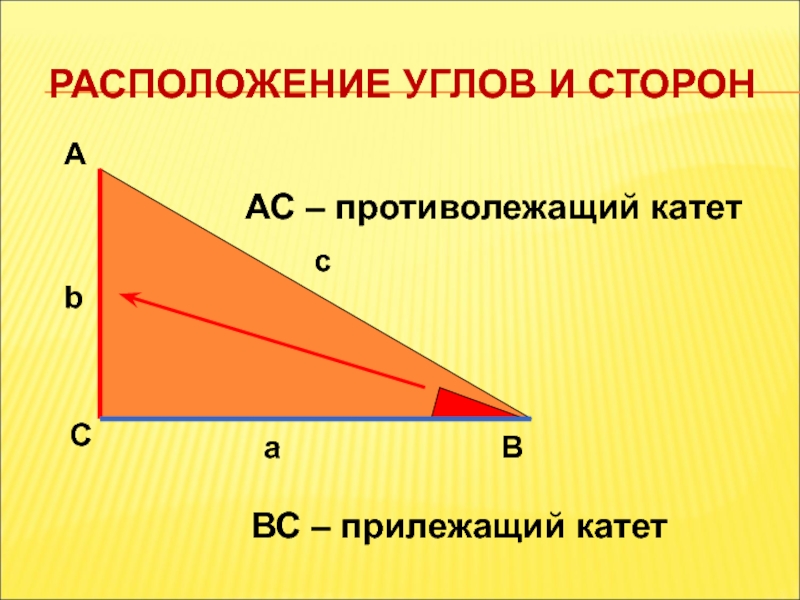
- 3. РАСПОЛОЖЕНИЕ УГЛОВ И СТОРОН А С
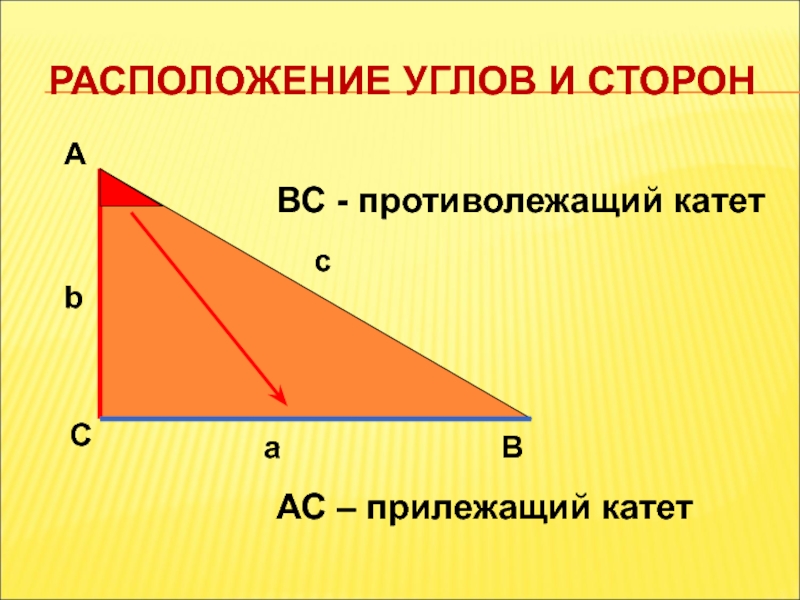
- 4. РАСПОЛОЖЕНИЕ УГЛОВ И СТОРОН А С
- 5. Синусом острого угла прямоугольного треугольника называется отношение
- 6. Косинусом острого угла прямоугольного треугольника называется отношение
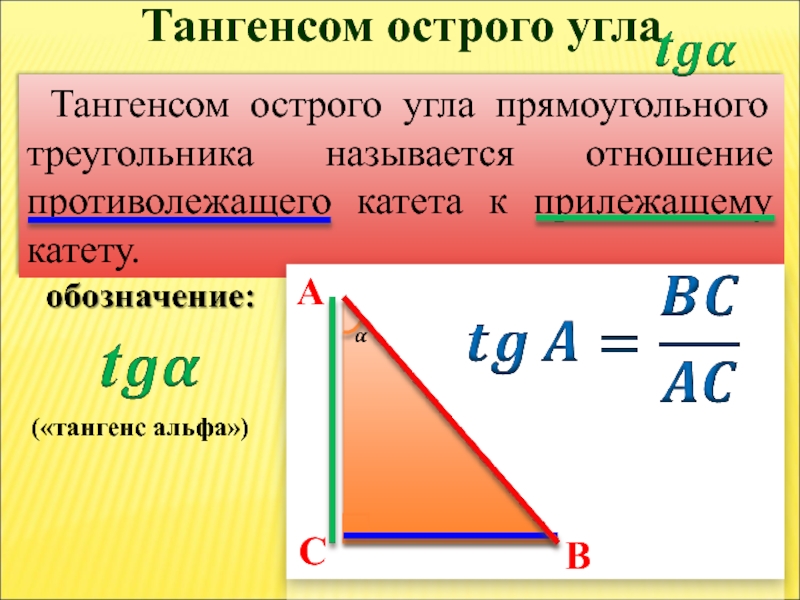
- 7. Тангенсом острого угла прямоугольного треугольника называется отношение
- 8. Тангенс угла равен отношению синуса к косинусу этого угла
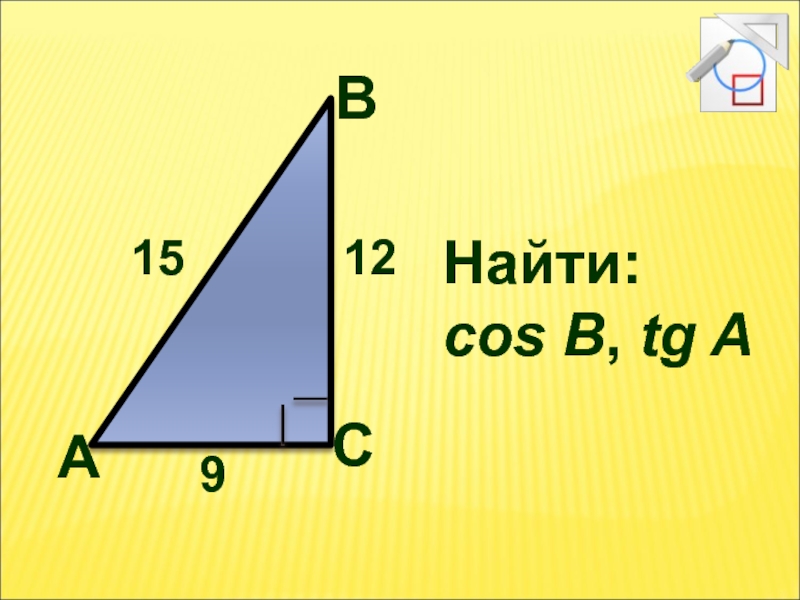
- 9. А В С 12 15 9 Найти: cos B, tg A
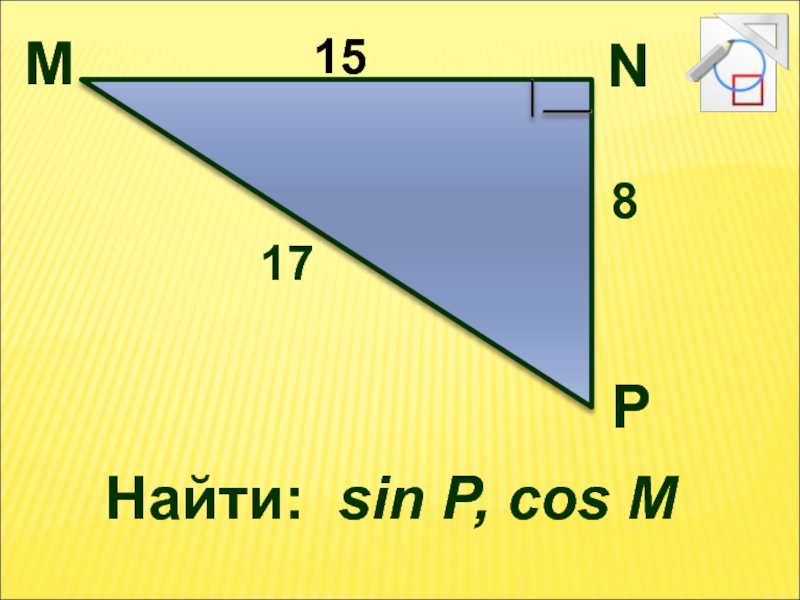
- 10. Найти: sin P, cos M M N P 15 17 8
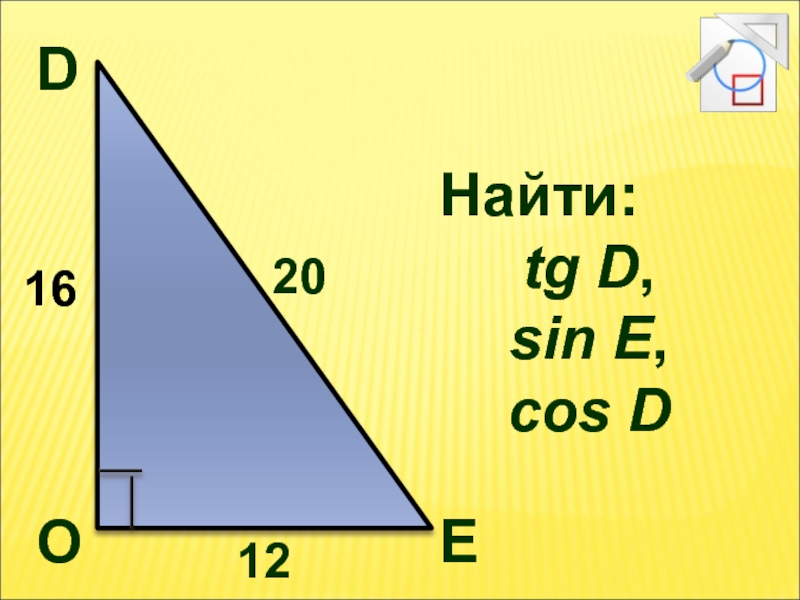
- 11. Найти: tg D, sin
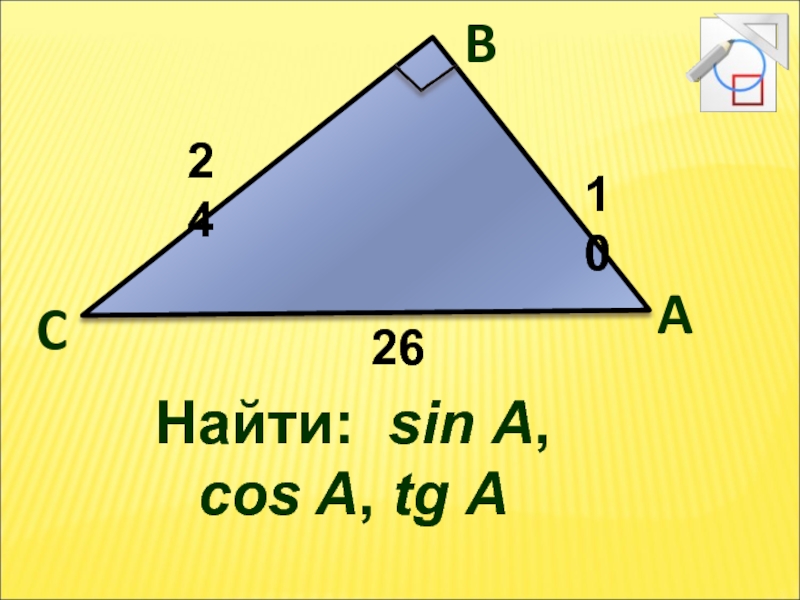
- 12. Найти: sin A, cos A, tg A A B C 24 10 26
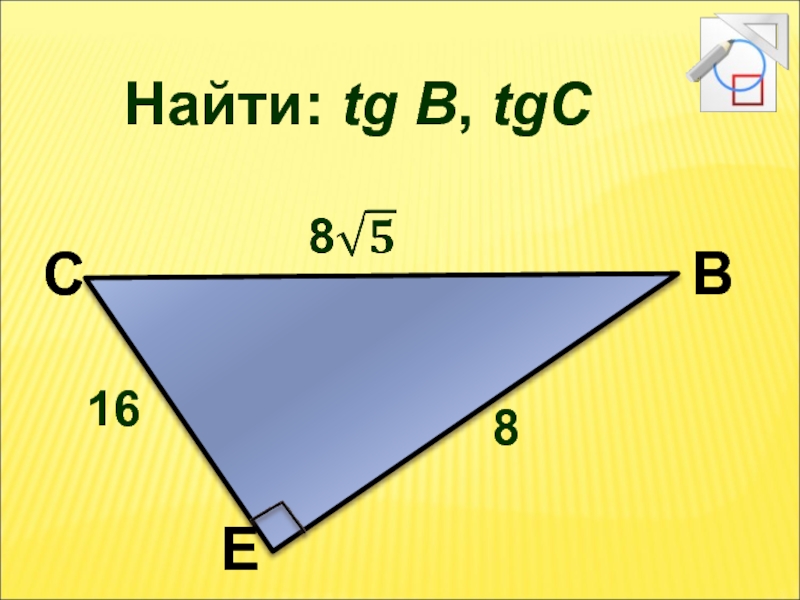
- 13. Найти: tg В, tgС 16 8 С В Е
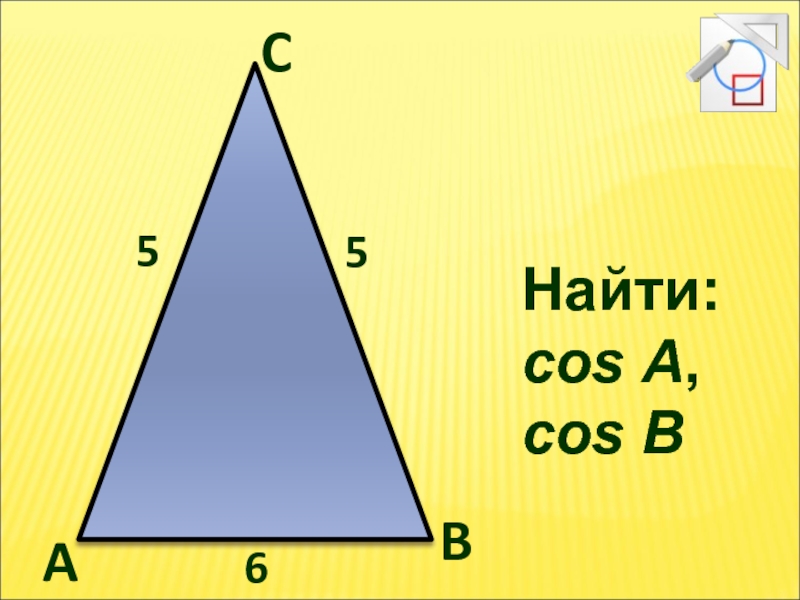
- 14. Найти: cos A, cos B 5 5 6 A C B
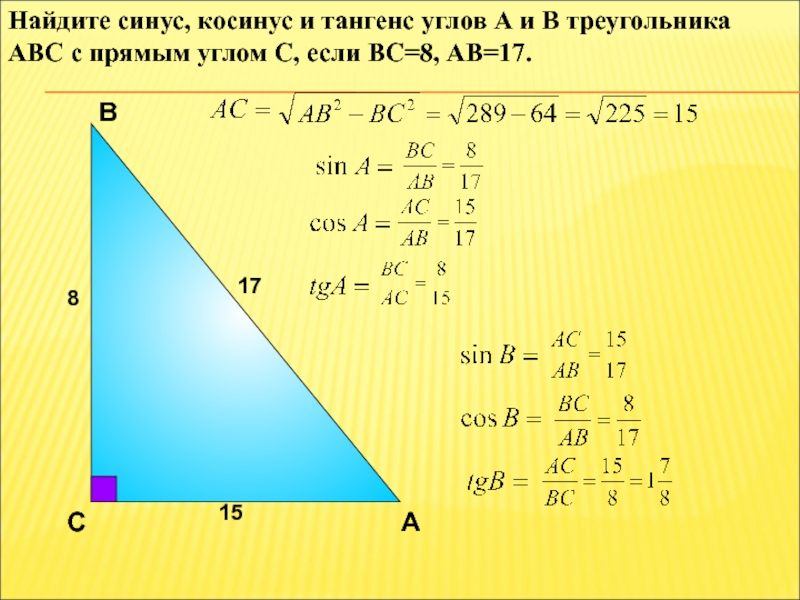
- 15. Найдите синус, косинус и тангенс углов А
- 16. А С В Если острый угол
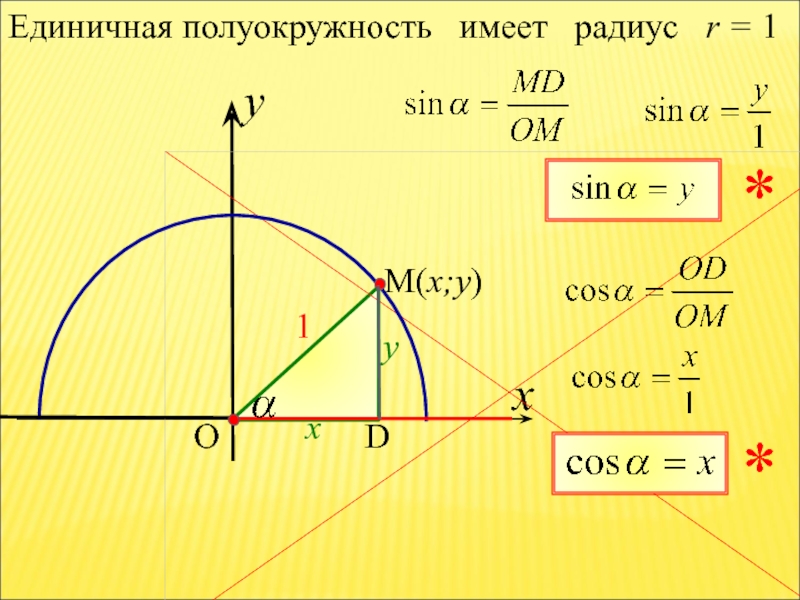
- 17. x Единичная полуокружность имеет
- 18. Для любого угла α
- 19. x y
- 20. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧКИ x
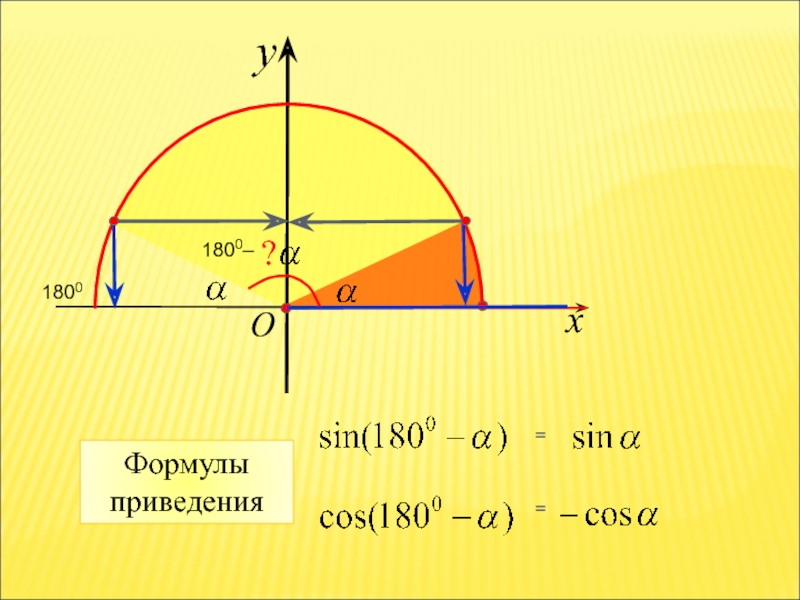
- 21. Основное тригонометрическое тождество. Формулы приведения
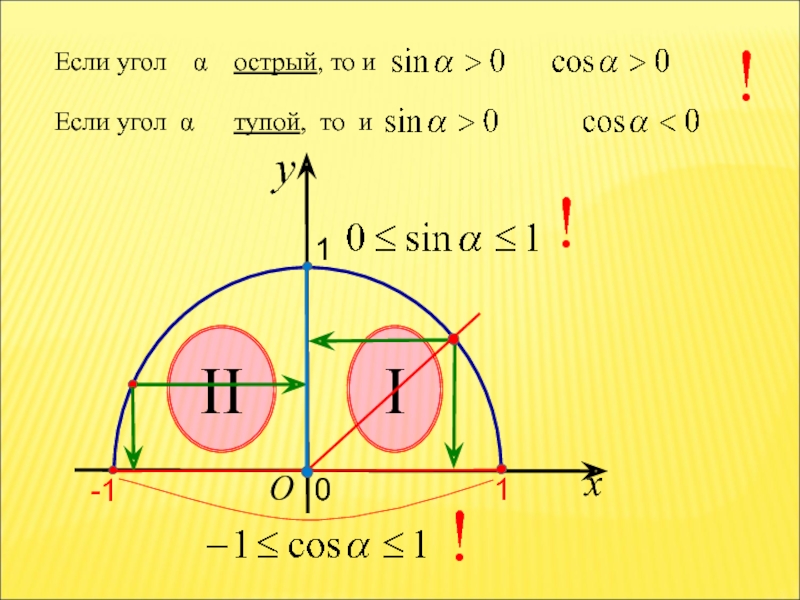
- 22. x Знаем, что y
- 23. Используем основное тригонометрическое тождество для определения положения
- 24. x y
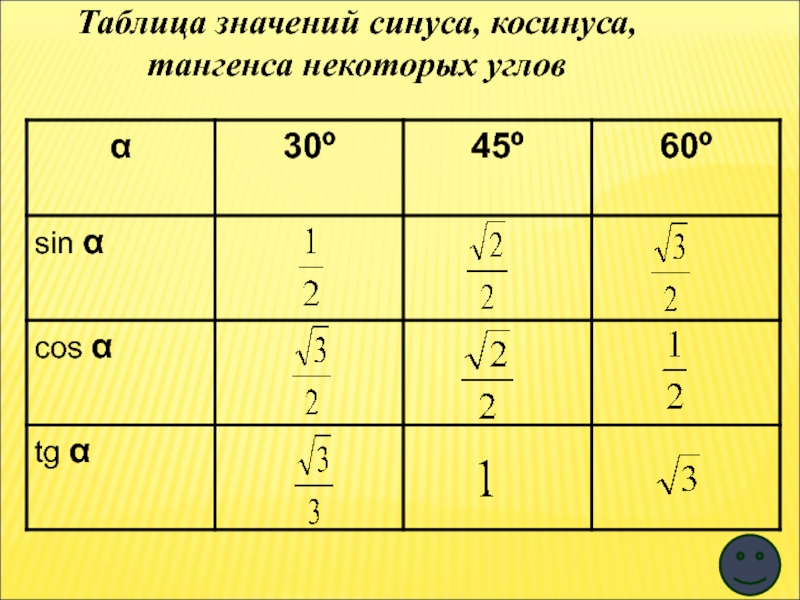
- 25. Таблица значений синуса, косинуса, тангенса некоторых углов
- 26. Применение формулы приведения Косинус тупого угла
- 27. Спасибо за урок!
Синус, косинус, тангенс острого угла прямоугольного треугольника
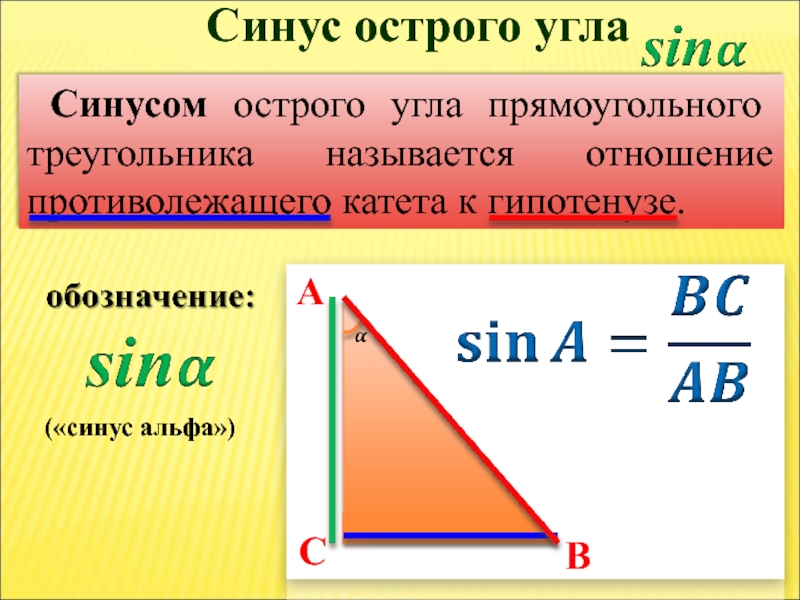
Слайд 5Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синус острого угла
A
B
C
(«синус альфа»)
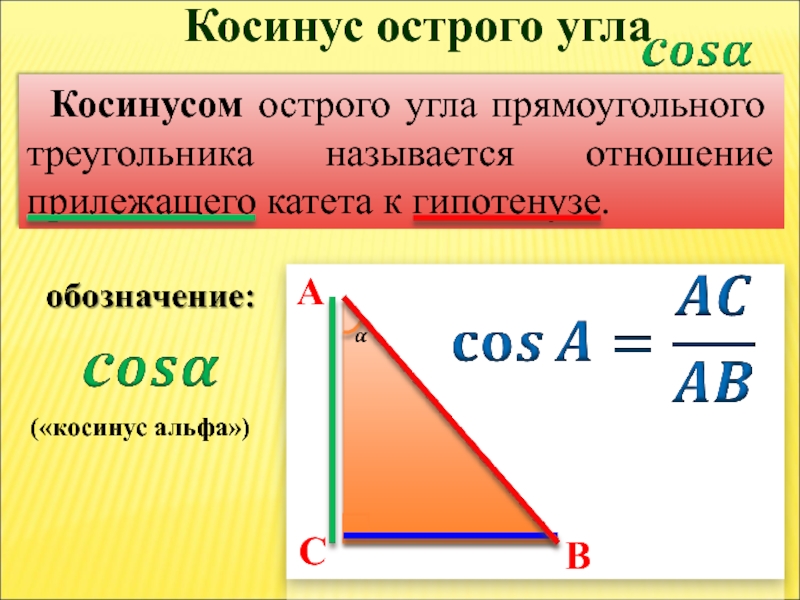
Слайд 6Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинус острого угла
A
B
C
(«косинус альфа»)
Слайд 7Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему
катету.
Тангенсом острого угла
A
B
C
(«тангенс альфа»)
Слайд 15Найдите синус, косинус и тангенс углов А и В треугольника АВС
с прямым углом С, если ВС=8, АВ=17.
А
В
С
17
8
15
Слайд 16
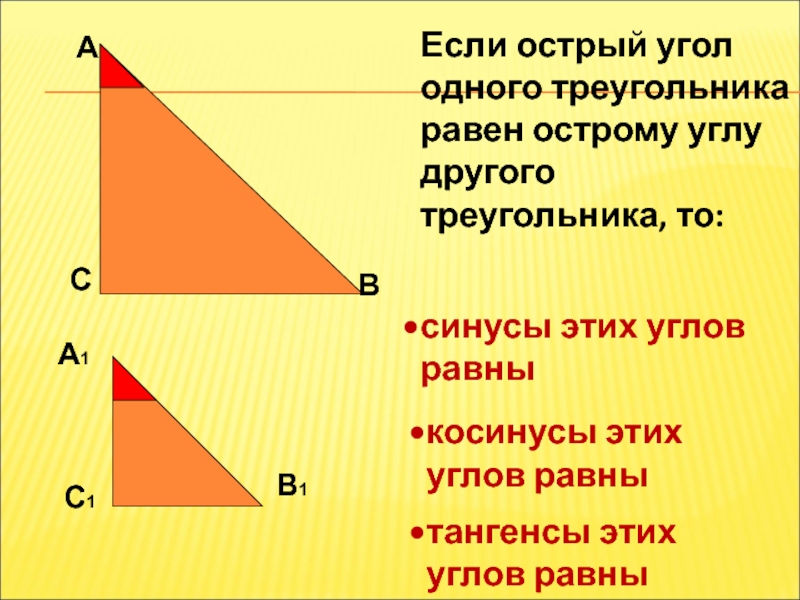
А
С
В
Если острый угол одного треугольника равен острому углу другого треугольника, то:
А1
В1
С1
синусы
этих углов равны
косинусы этих углов равны
тангенсы этих углов равны
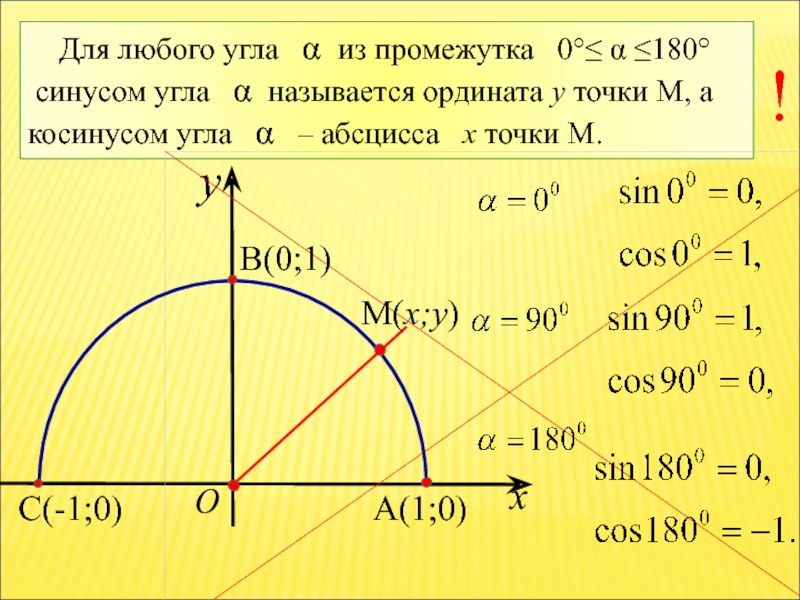
Слайд 18 Для любого угла α из промежутка 0°≤
α ≤180°
синусом угла α называется ордината y точки М, а косинусом угла α – абсцисса x точки М.
синусом угла α называется ордината y точки М, а косинусом угла α – абсцисса x точки М.
x
y
A(1;0)
В(0;1)
O
С(-1;0)
!
M(x;y)
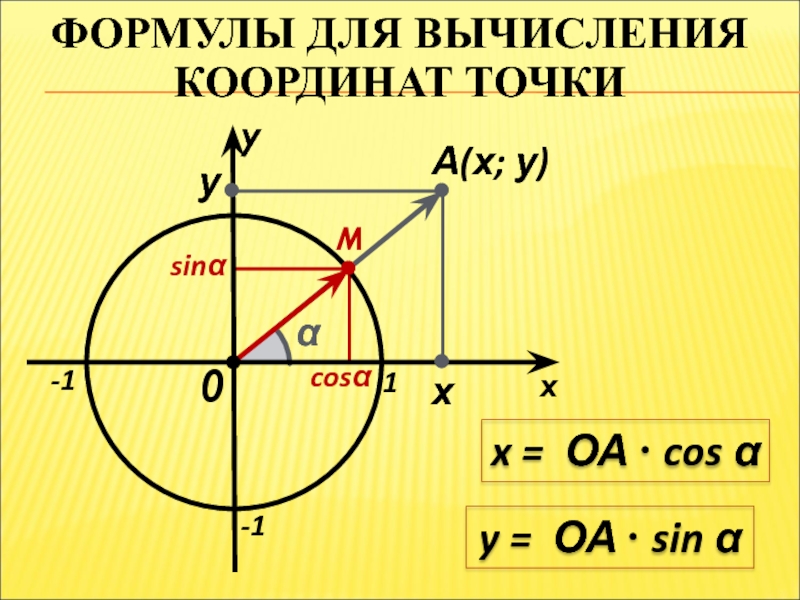
Слайд 20ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧКИ
x
1
-1
-1
А(х; у)
0
α
y
cosα
sinα
x = ОА ∙ cos α
y
= ОА ∙ sin α
х
y
M
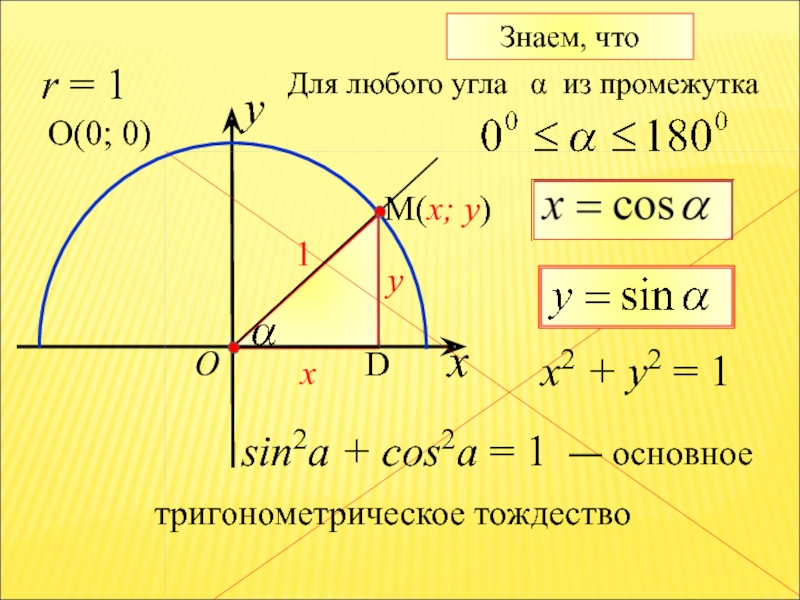
Слайд 22x
Знаем, что
y
O
x
y
1
x2 + y2 = 1
r = 1
О(0; 0)
sin2a
+ cos2a = 1
― основное
Для любого угла α из промежутка
тригонометрическое тождество
Слайд 23Используем основное тригонометрическое тождество для определения положения точки
M ( x; y
)
в прямоугольной системе координат
в прямоугольной системе координат
sin2a + cos2a = 1
Для любого угла α из промежутка
Слайд 26Применение формулы
приведения
Косинус тупого угла равен «–» косинусу смежного с ним
острого угла. Вычислим быстро!
