Zemkoho, Professor Jörg Fliege
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Solution methods for bilevel optimization презентация
Содержание
- 1. Solution methods for bilevel optimization
- 2. Overview Definition of a bilevel problem and
- 3. Stackelberg Game (Bilevel problem) Players:
- 4. Example Taxation of a factory Leader –
- 5. General structure of a Bilevel problem
- 6. Important Sets
- 7. General linear Bilevel problem
- 8. Solution methods Vertex enumeration in
- 9. Concept of KKT conditions
- 10. Value function reformulation
- 11. KKT for value function reformulation
- 12. Assumptions
- 13. KKT-type optimality conditions for Bilevel
- 14. Further Assumptions (for simpler version)
- 15. Simpler version of KKT-type conditions
- 16. NCP-Functions
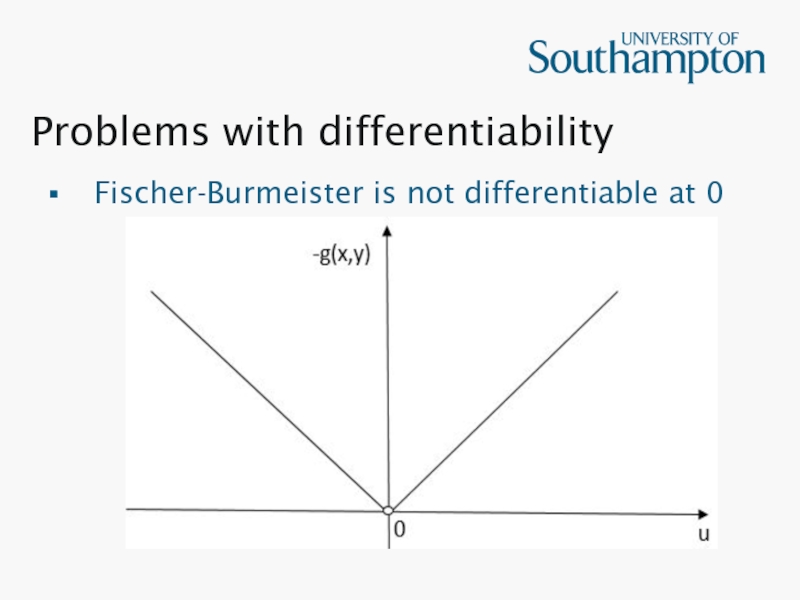
- 17. Problems with differentiability Fischer-Burmeister is not differentiable at 0
- 18.
- 19. Simpler version with perturbed Fischer-Burmeister NCP functions
- 20. Iterative methods
- 21. Newton method
- 22. Pseudo inverse
- 23. Gauss-Newton method
- 24. Singular Value Decomposition (SVD)
- 25. SVD for wrong direction
- 26. SVD for right direction
- 27. Levenberg-Marquardt method
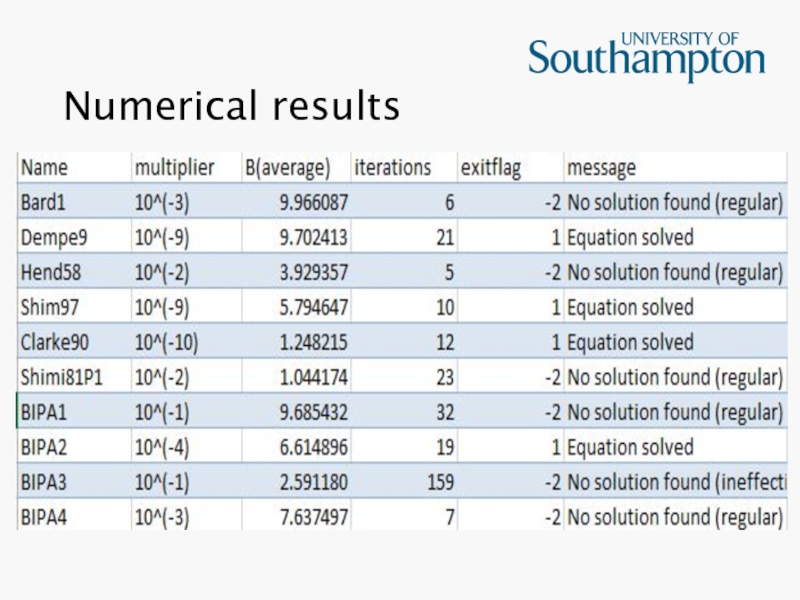
- 28. Numerical results
- 29. Plans for further work
- 30. Plans for further work 6.
- 31. Thank you! Questions?
- 32. References
- 33. References
Overview Definition of a bilevel problem and its general form Optimality (KKT-type) conditions Reformulation of a general bilevel problem Iterative (descent direction) methods Numerical results
Слайд 1Solution Methods for Bilevel Optimization
Andrey Tin
A.Tin@soton.ac.uk
School of Mathematics
Supervisors: Dr Alain B.
Слайд 2Overview
Definition of a bilevel problem and its general form
Optimality (KKT-type) conditions
Reformulation
of a general bilevel problem
Iterative (descent direction) methods
Numerical results
Iterative (descent direction) methods
Numerical results
Слайд 3Stackelberg Game (Bilevel problem)
Players: the Leader and the Follower
The Leader is
first to make a decision
Follower reacts optimally to Leader’s decision
The payoff for the Leader depends on the follower’s reaction
Follower reacts optimally to Leader’s decision
The payoff for the Leader depends on the follower’s reaction
Слайд 4Example
Taxation of a factory
Leader – government
Objectives: maximize profit and minimize pollution
Follower
– factory owner
Objectives: maximize profit
Objectives: maximize profit
Слайд 8Solution methods
Vertex enumeration in the context of Simplex method
Kuhn-Tucker approach
Penalty approach
Extract
gradient information from a lower objective function to compute directional derivatives of an upper objective function
Слайд 30Plans for further work
6. Construct the own code for Levenberg-Marquardt method
in the context of solving bilevel problems within defined reformulation.
7. Search for good starting point techniques for our problem. 8. Do the numerical calculations for the harder reformulation defined .
9. Code Newton method with pseudo-inverse.
10. Solve the problem assuming strict complementarity
11. Look at other solution methods.
7. Search for good starting point techniques for our problem. 8. Do the numerical calculations for the harder reformulation defined .
9. Code Newton method with pseudo-inverse.
10. Solve the problem assuming strict complementarity
11. Look at other solution methods.
