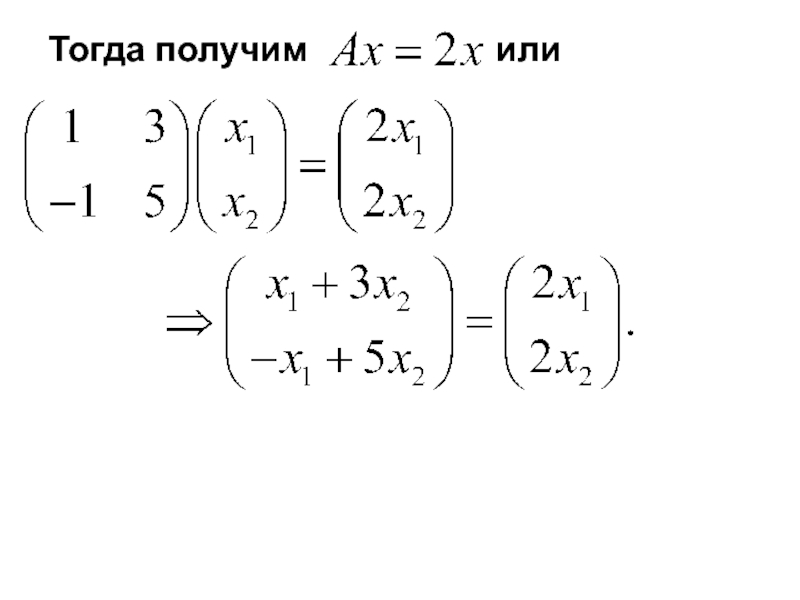матрицы
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Собственные значения и собственные векторы матрицы презентация
Содержание
- 1. Собственные значения и собственные векторы матрицы
- 2. Пусть - матрица,
- 3. Например, если
- 4. Рассмотрим Запишем матричное уравнение в координатной форме.
- 5. Преобразуем
- 6. Получилась система линейных однородных уравнений. Такая система
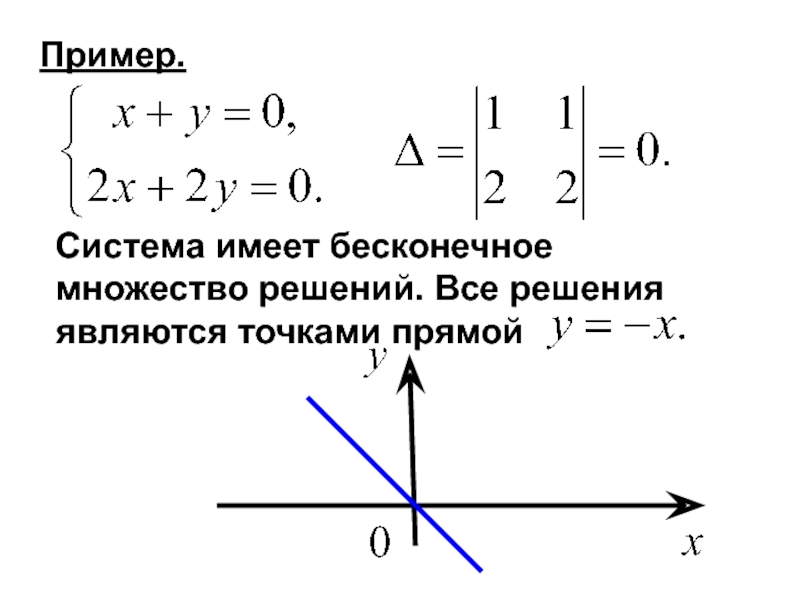
- 7. Пример. Система имеет бесконечное множество решений. Все решения являются точками прямой
- 8. Вернемся к нашей системе. Составим определитель системы
- 9. Примеры. 1. Найти собственные значения матрицы Запишем матрицу
- 10. Находим корни характеристического уравнения или Мы нашли собственные значения. Ответ:
- 11. Нахождение собственных векторов 1. Найдем собственный вектор,
- 12. Тогда получим или
- 13. Отсюда Положим тогда Получилось
- 14. Можно считать, что мы нашли собственный вектор.
- 15. Получим - собственный вектор, соответствующий собственному значению
- 16. Аналогично найдем т.е. собственный вектор, соответствующий
- 17. Пусть тогда Нормируем, т.е. разделим на Получим
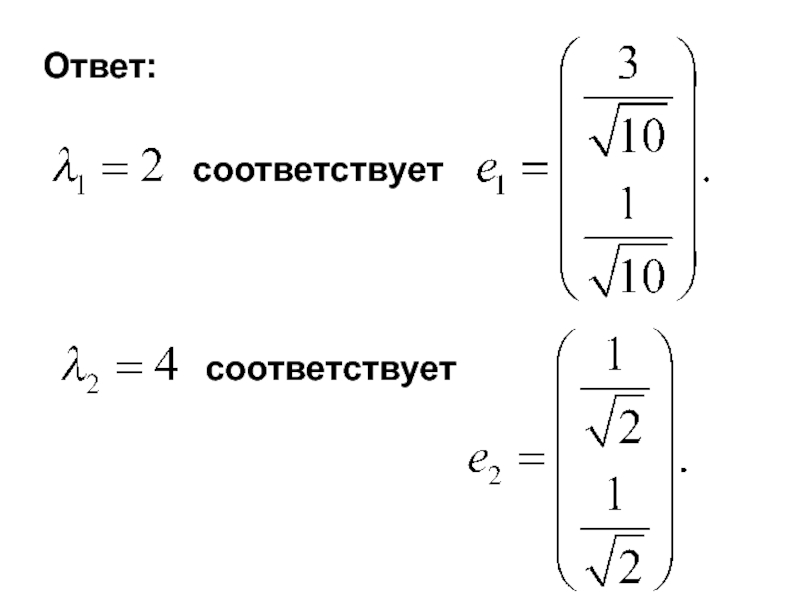
- 18. Ответ: соответствует соответствует
- 19. Функция. Предел функции в точке. Односторонние пределы.
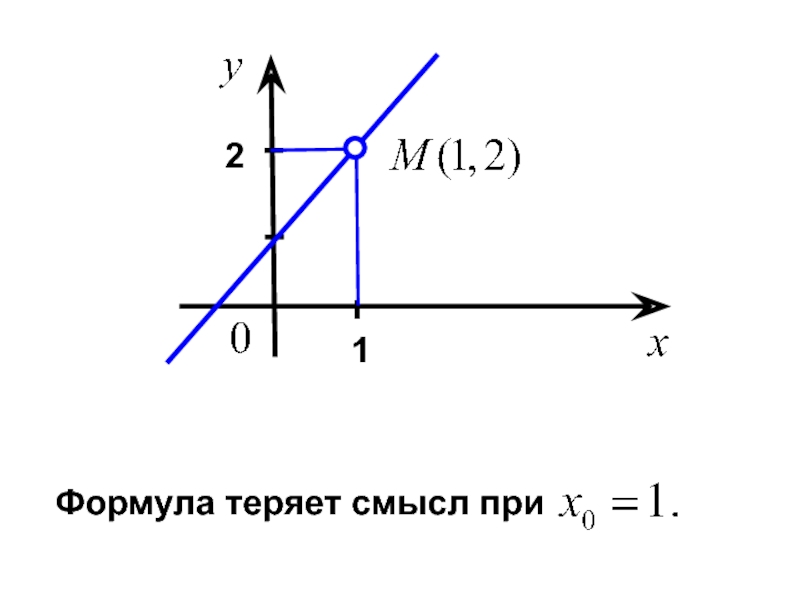
- 20. 1. Предел в точке. Рассмотрим пример. Построить график функции
- 21. 1 2
- 22. В этом случае пишут: По-другому: при
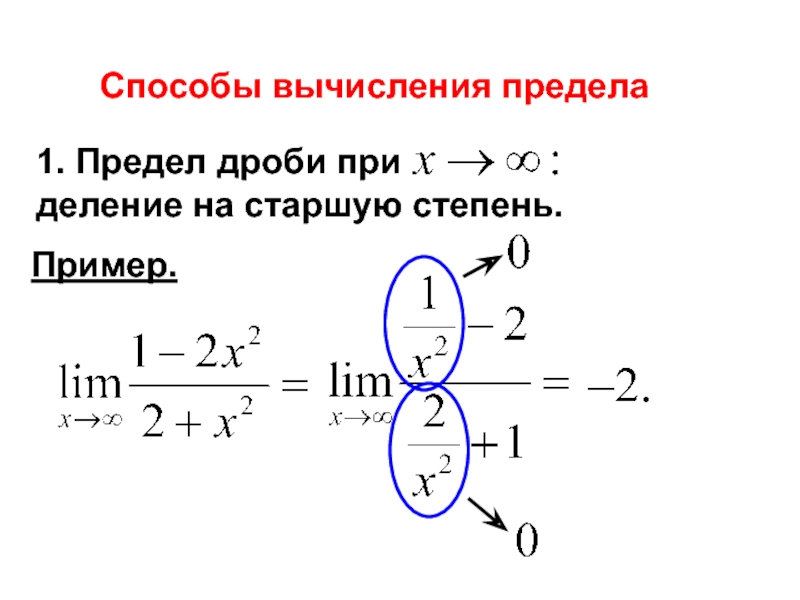
- 23. Способы вычисления предела 1. Предел дроби при
- 24. 2. Разложение на множители, когда Пример.
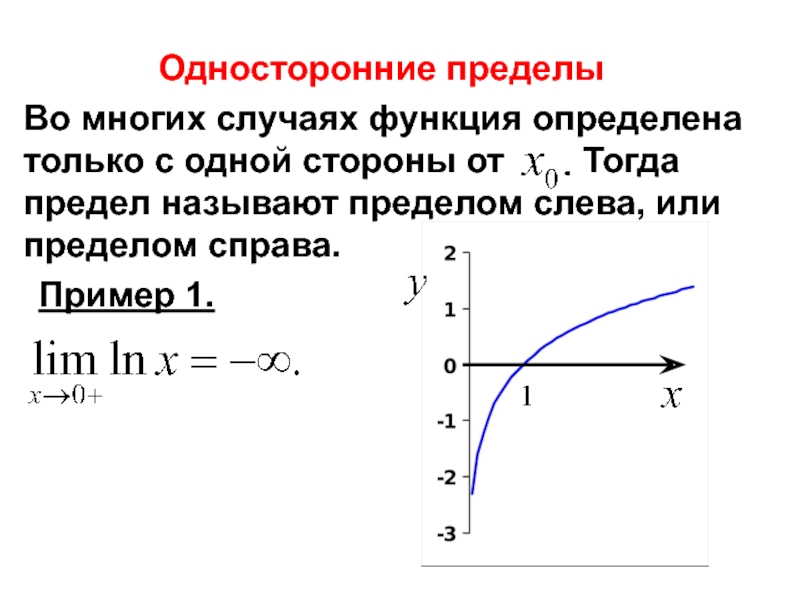
- 25. Односторонние пределы Пример 1.
- 26. Пример 2.
- 27. Опр. Функция
- 28. Опр. Если в точке
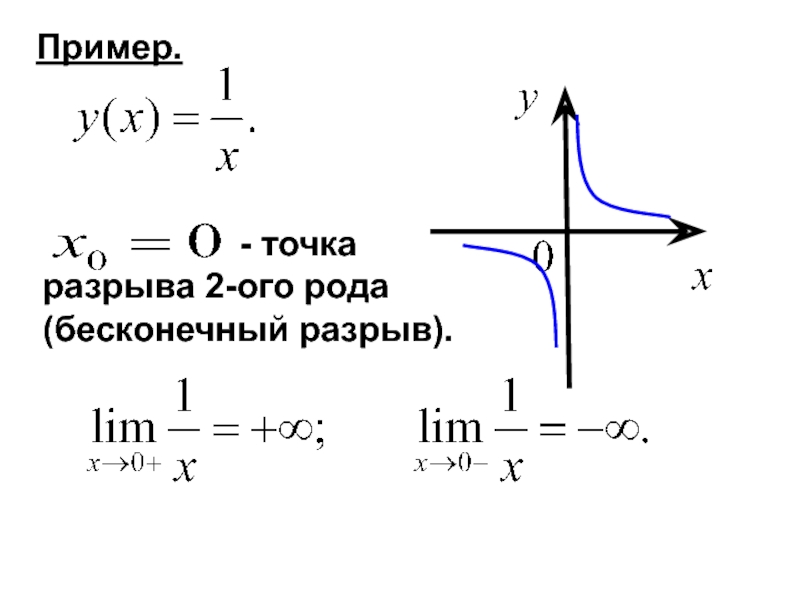
- 29. Пример.
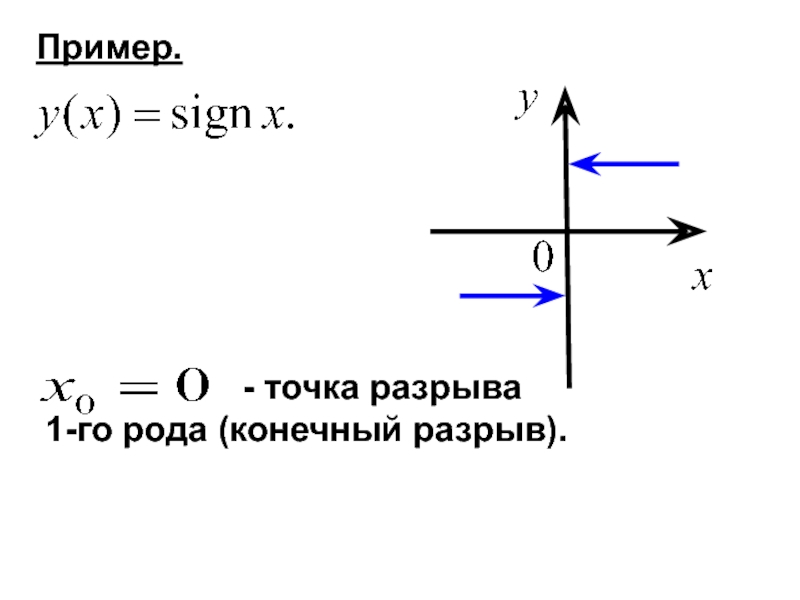
- 30. Пример.
Пусть - матрица, - вектор, - число. Рассмотрим уравнение называется собственным значением,
Слайд 1Лекция №10
Лектор: доц. Лаптева Надежда Александровна
Тема: Собственные значения и собственные векторы
Слайд 2Пусть - матрица, -
вектор,
- число.
- число.
Рассмотрим уравнение
называется собственным значением, - собственным вектором.
Такое преобразование изменяет длину вектора в раз.
Слайд 3Например, если то
т.е. длина вектора увеличивается в 2 раза.
Если же то длина вектора
уменьшается в 2 раза.
Слайд 6Получилась система линейных однородных уравнений. Такая система всегда имеет нулевое решение.
Нас интересует случай, когда система имеет ненулевое решение.
Теорема. Система линейных уравнений имеет ненулевое решение, если её определитель равен нулю.
Слайд 8Вернемся к нашей системе. Составим определитель системы
или
Получилось квадратное уравнение. Такое уравнение
называется характеристическим. Корни уравнения – это собственные значения матрицы
Слайд 11Нахождение собственных векторов
1. Найдем собственный вектор, соответствующий собственному значению
Рассмотрим уравнение
и вместо подставим
Слайд 14Можно считать, что мы нашли собственный вектор. Но обычно этот вектор
нормируют, т.е. приводят его к вектору единичной длины. Для этого найдем длину вектора
и каждую координату разделим на
и каждую координату разделим на
Слайд 19Функция. Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность
функции. Точки разрыва функции и их классификация.
Слайд 27Опр. Функция
называется непрерывной в точке если
Все элементарные функции непрерывны на своей области определения.
Пример.
- непрерывные функции.
Слайд 28Опр. Если в точке функция не является непрерывной,
то - точка разрыва.
Рассматриваются точки разрыва 1-го и 2-ого рода.
