- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия, планиметрия, стереометрия презентация
Содержание
- 1. Геометрия, планиметрия, стереометрия
- 2. Геометрия Планиметрия Стереометрия stereos - телесный, твердый, объемный, пространственный metreo - измерять
- 3. Стереометрия. Раздел геометрии, в котором
- 4. Обозначение основных фигур в пространстве:
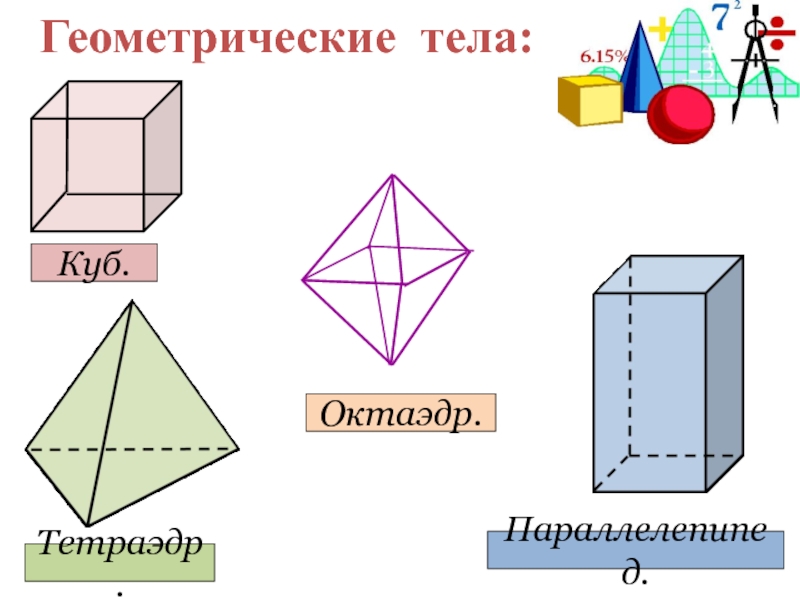
- 5. Геометрические тела: Куб. Параллелепипед. Тетраэдр. Октаэдр.
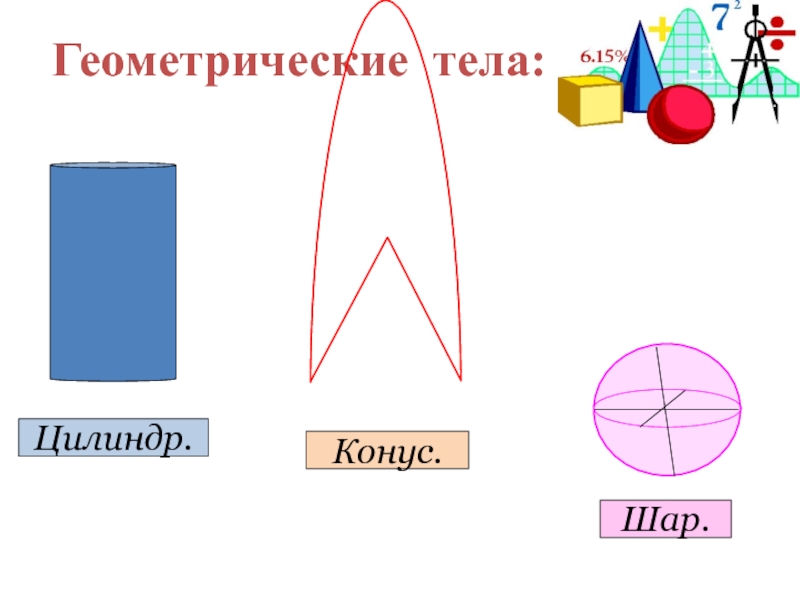
- 6. Геометрические тела: Цилиндр. Конус. Шар.
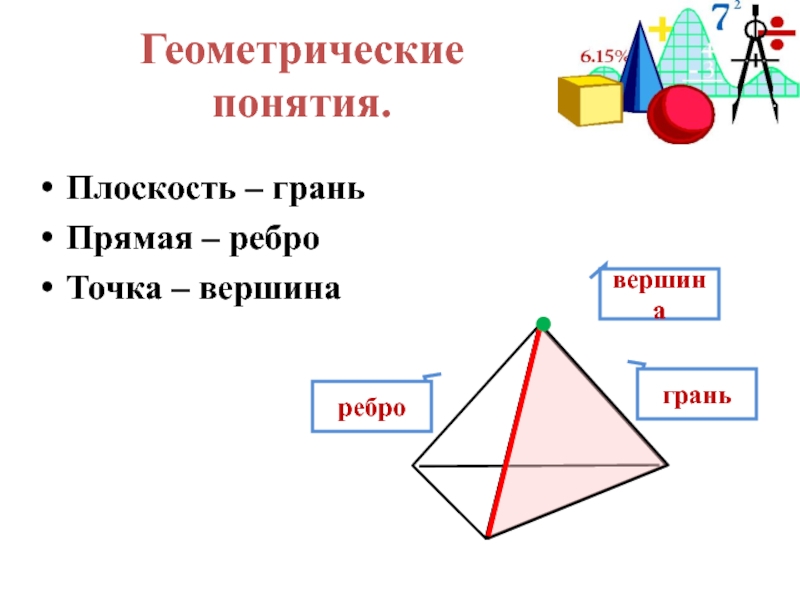
- 7. Геометрические понятия. Плоскость – грань Прямая –
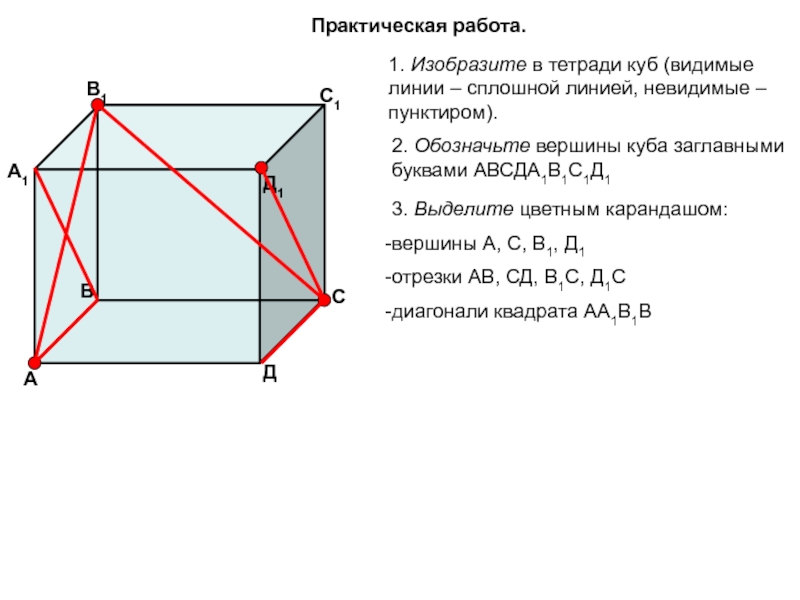
- 8. Практическая работа. 1. Изобразите в тетради куб
- 9. Аксиома (от греч. axíõma – принятие положения) исходное положение научной теории, принимаемое без доказательства
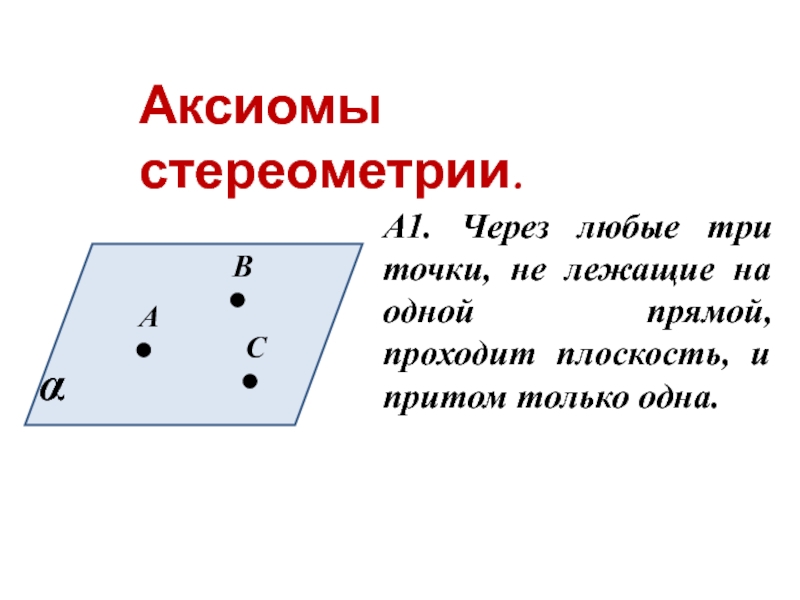
- 10. Аксиомы стереометрии. А1. Через любые три
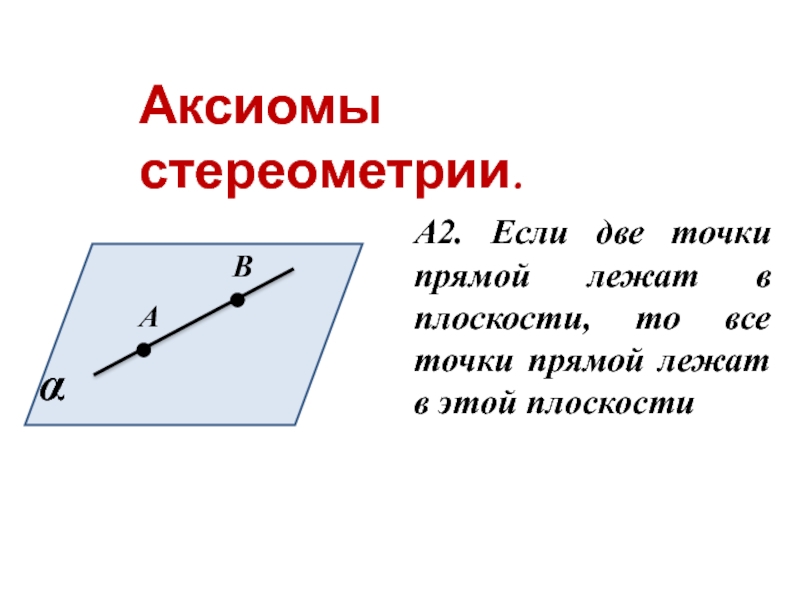
- 11. Аксиомы стереометрии. А2. Если две точки прямой
- 12. Аксиомы стереометрии. А3. Если две плоскости
- 13. Аксиомы стереометрии описывают:
- 14. Взаимное расположение прямой и плоскости. Прямая лежит
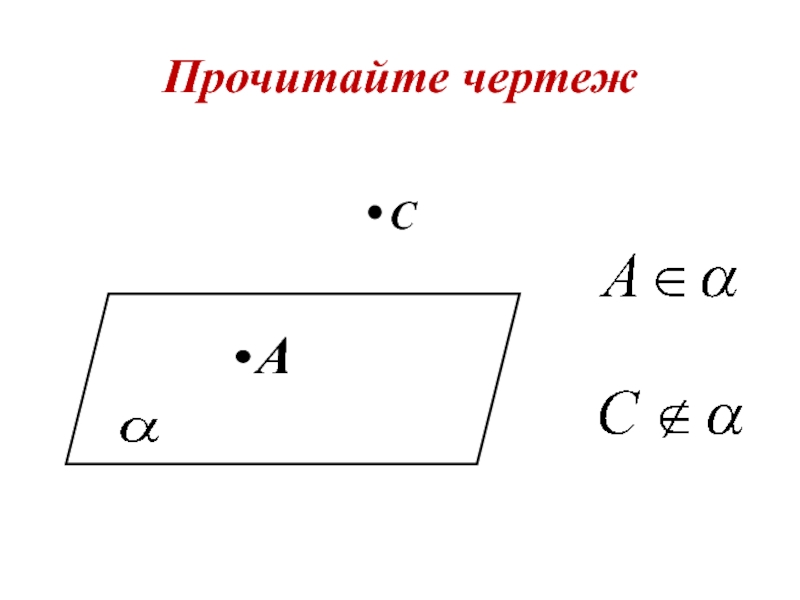
- 15. Прочитайте чертеж A С
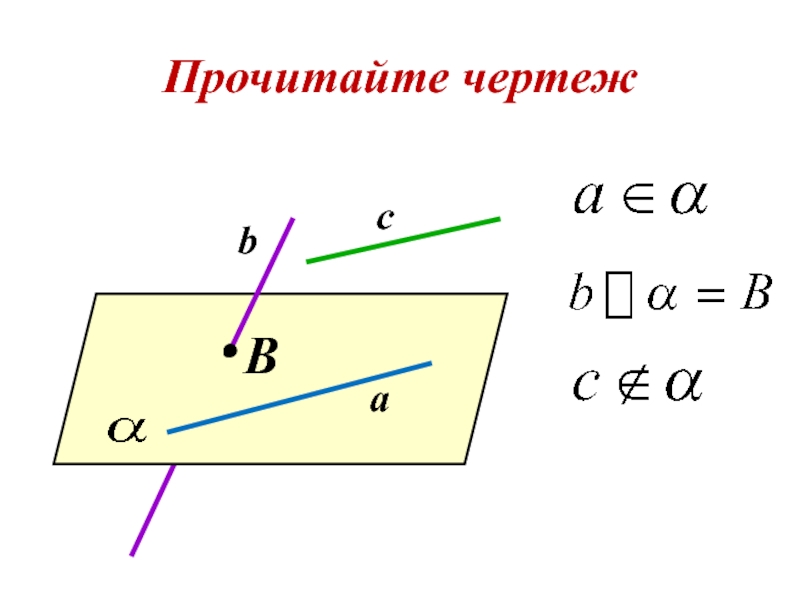
- 16. Прочитайте чертеж B c b a
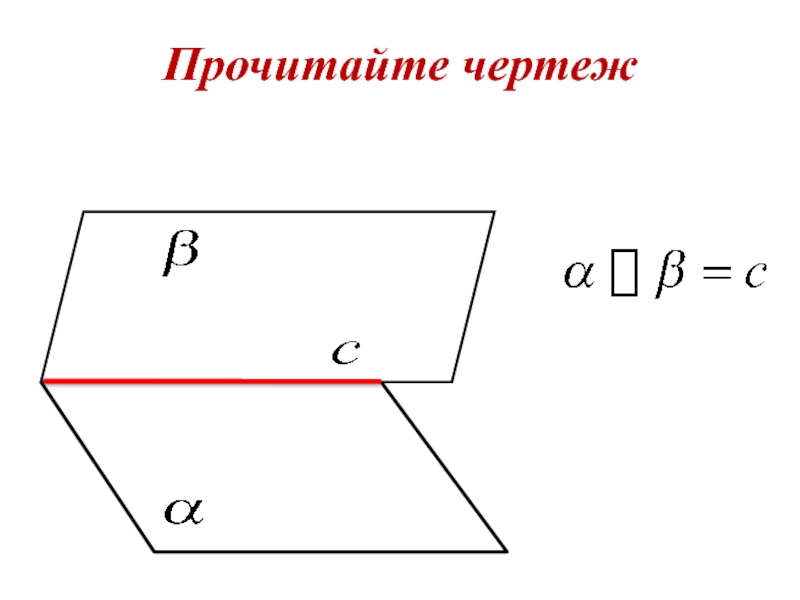
- 17. Прочитайте чертеж
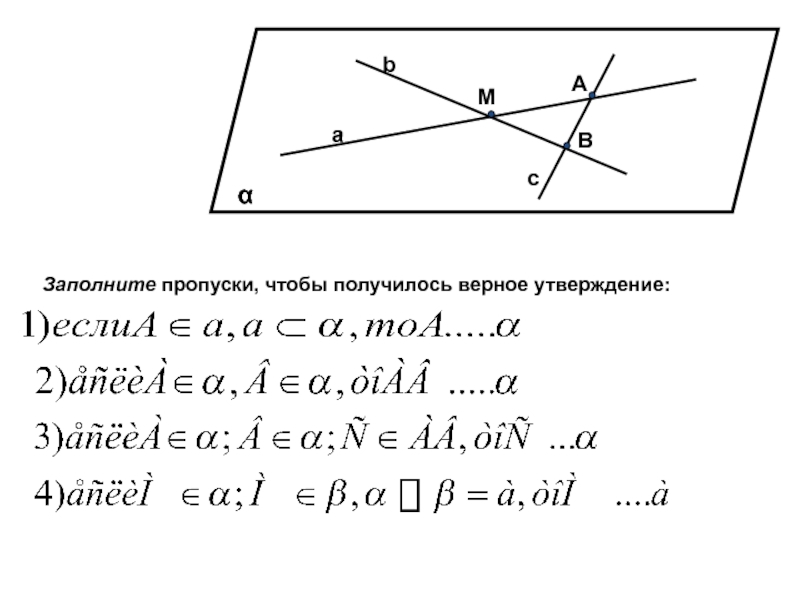
- 18. α А М
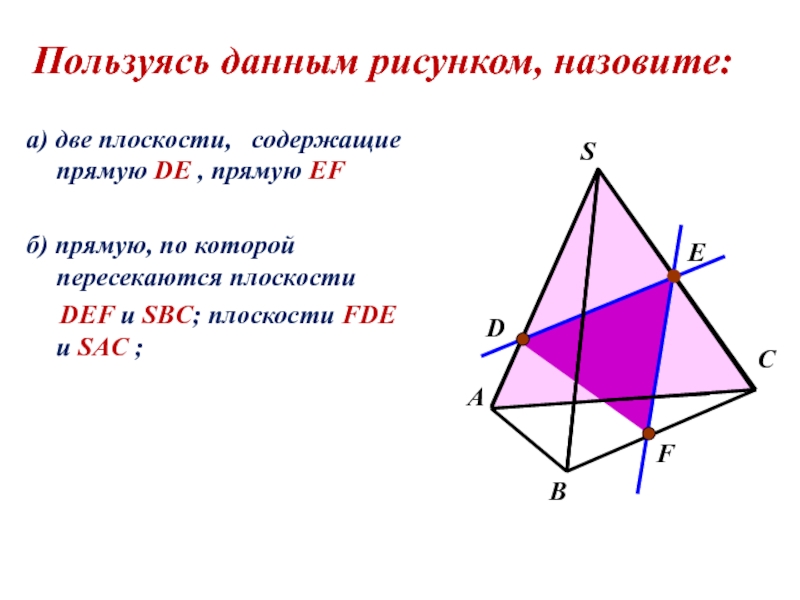
- 19. а) две плоскости,
- 20. а) Две плоскости, cодержащие
- 21. а) Две плоскости,
- 22. Теорема 1.Через прямую и не лежащую на
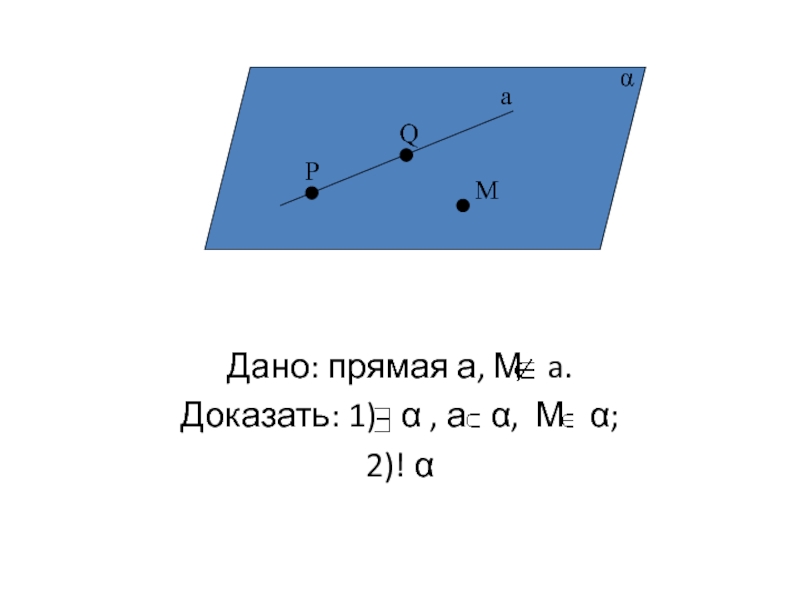
- 23. Дано: прямая а, М a. Доказать:
- 24. Доказательство. Возьмем точки Р a, Q
- 25. Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
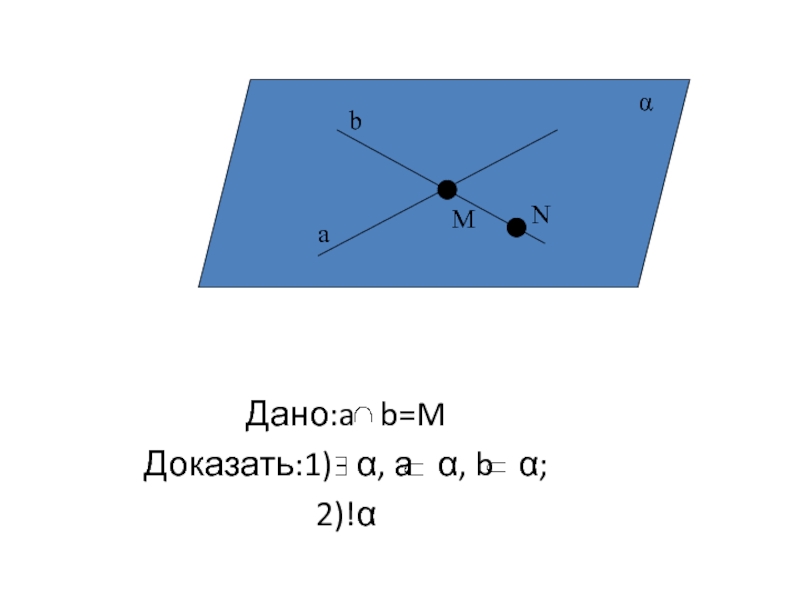
- 26. Дано:a b=M Доказать:1) α, а
- 27. Доказательство Возьмем точку N b. По Т1
- 28. Способы задания плоскости в пространстве.
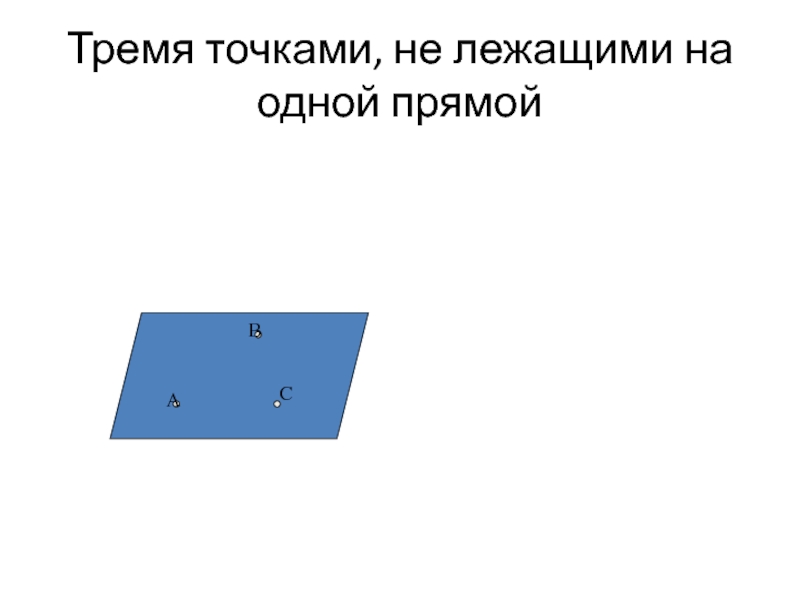
- 29. Тремя точками, не лежащими на одной прямой A B C
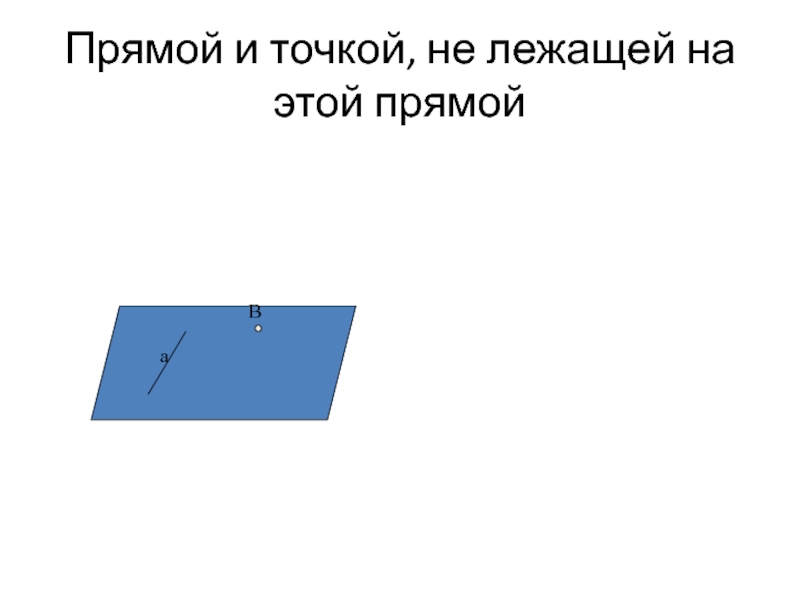
- 30. Прямой и точкой, не лежащей на этой прямой B a
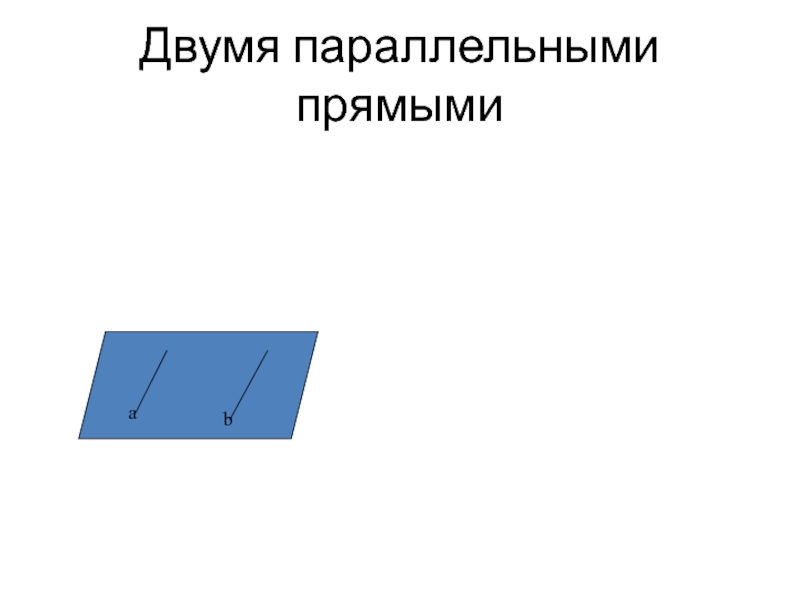
- 31. Двумя параллельными прямыми a b
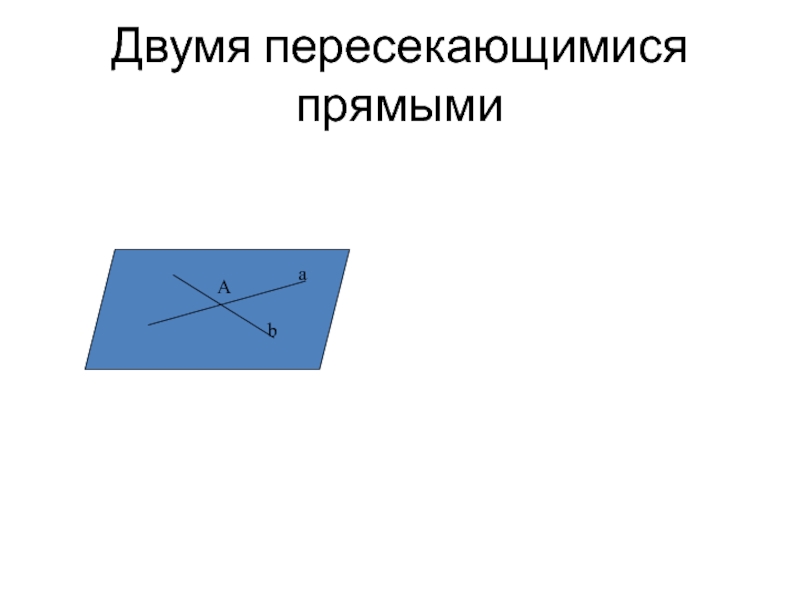
- 32. Двумя пересекающимися прямыми A a b
- 33. Домашнее задание: П. 1-2-3
Геометрия Планиметрия Стереометрия stereos - телесный, твердый, объемный, пространственный metreo - измерять
Слайд 2Геометрия
Планиметрия
Стереометрия
stereos - телесный, твердый, объемный, пространственный
metreo - измерять
Слайд 3
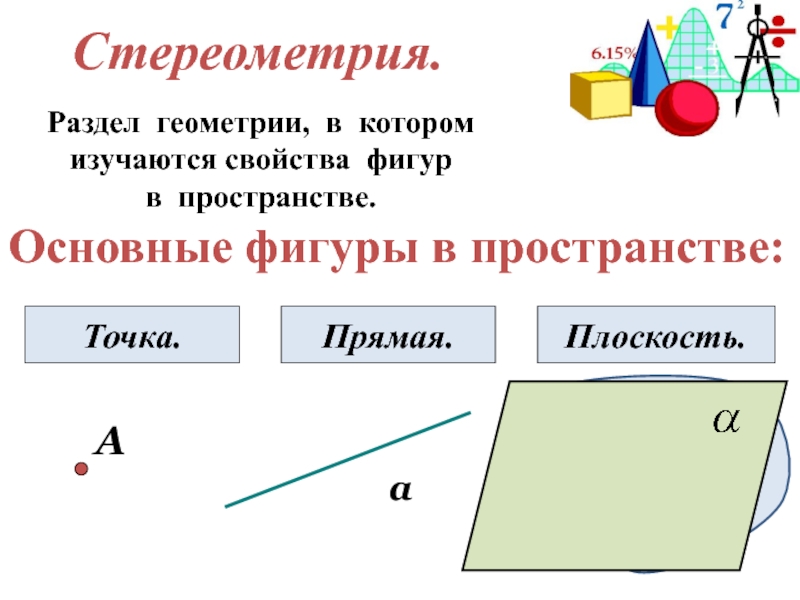
Стереометрия.
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в
пространстве:
А
Точка.
а
Прямая.
Плоскость.
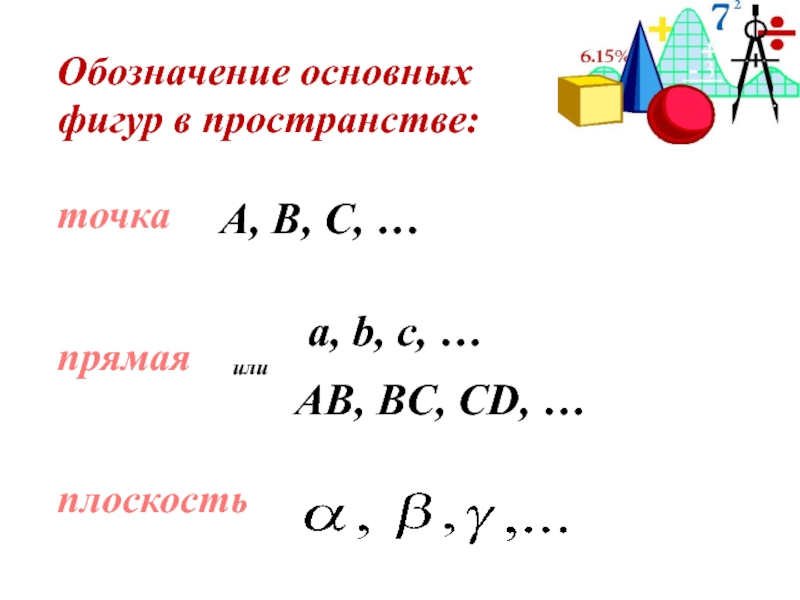
Слайд 4Обозначение основных
фигур в пространстве:
точка
прямая
плоскость
A, B, C, …
a, b, c, …
или
AВ,
BС, CD, …
Слайд 8Практическая работа.
1. Изобразите в тетради куб (видимые линии – сплошной линией,
невидимые – пунктиром).
2. Обозначьте вершины куба заглавными буквами АВСДА1В1С1Д1
А
В
С
Д
Д1
С1
В1
А1
3. Выделите цветным карандашом:
вершины А, С, В1, Д1
отрезки АВ, СД, В1С, Д1С
диагонали квадрата АА1В1В
Слайд 9Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без
доказательства
Слайд 10
Аксиомы стереометрии.
А1. Через любые три точки, не лежащие на одной прямой,
проходит плоскость, и притом только одна.
α
А
В
С
Слайд 11Аксиомы стереометрии.
А2. Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости
α
А
В
Слайд 12
Аксиомы стереометрии.
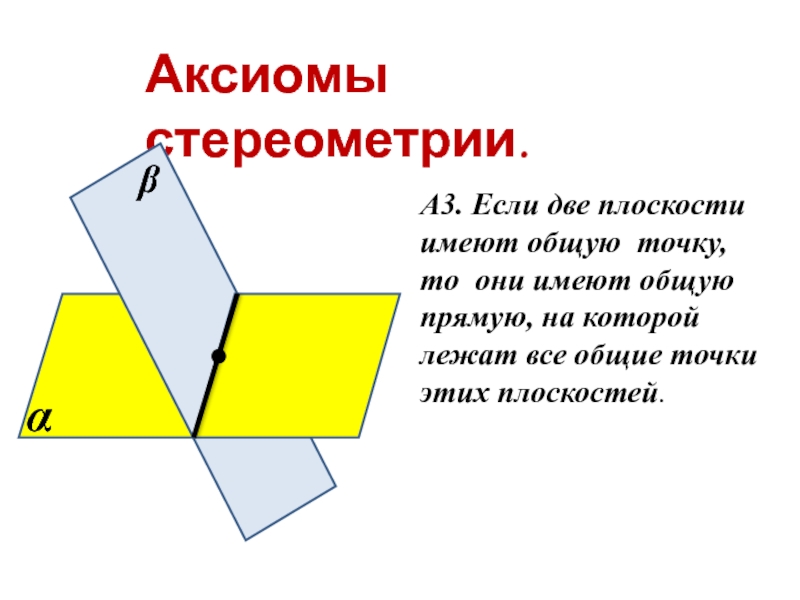
А3. Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих плоскостей.
α
β
Слайд 13
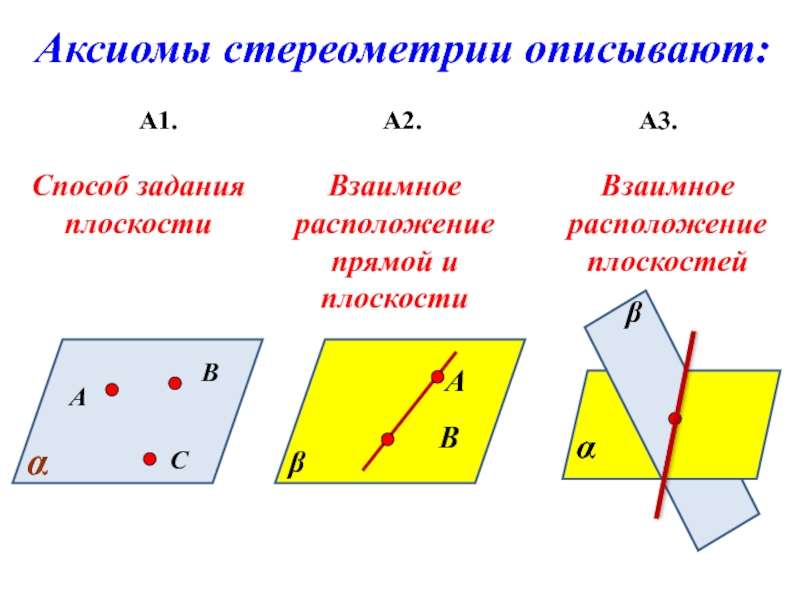
Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
α
Способ задания плоскости
β
А
В
Взаимное расположение прямой и плоскости
Взаимное
расположение плоскостей
α
β
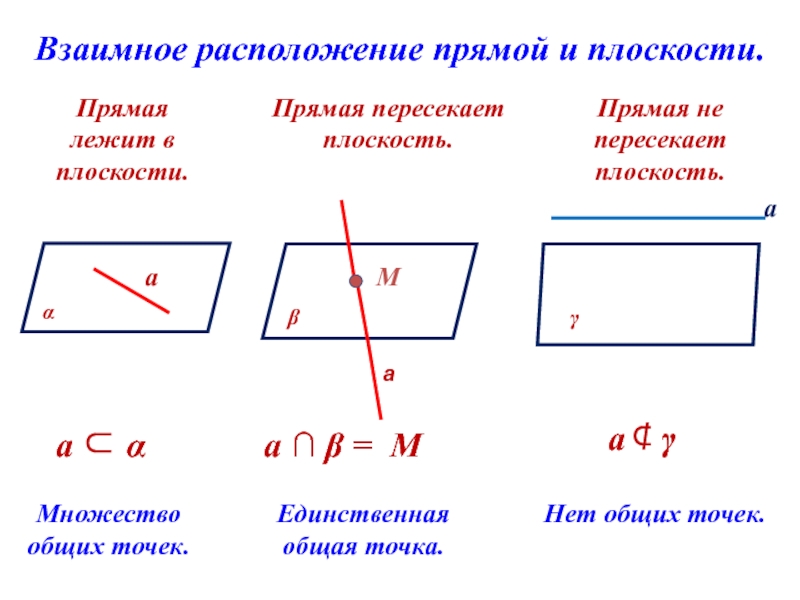
Слайд 14Взаимное расположение прямой и плоскости.
Прямая лежит в плоскости.
Прямая пересекает плоскость.
Прямая не
пересекает плоскость.
Множество общих точек.
Единственная общая точка.
Нет общих точек.
α
а
β
а
М
γ
а
а ⊂ α
а ∩ β = М
а ⊄ γ
Слайд 19
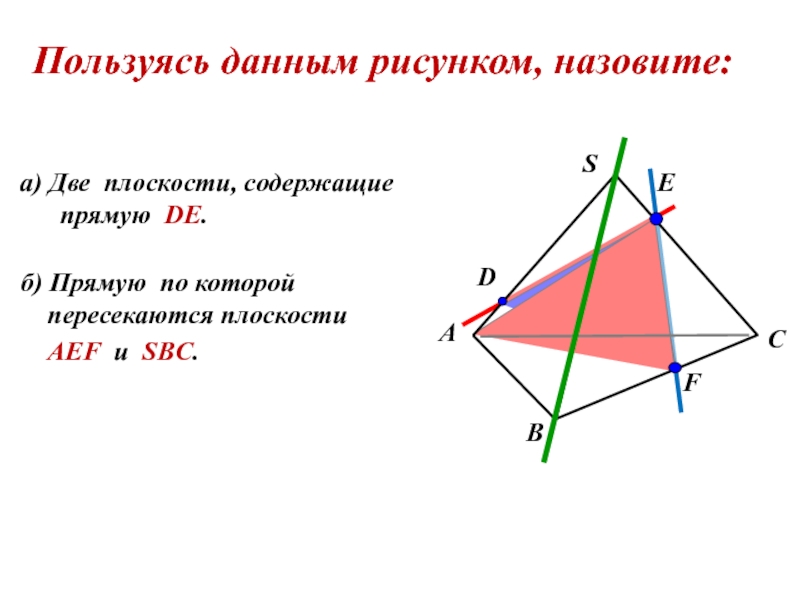
а) две плоскости, содержащие прямую DE , прямую EF
б) прямую,
по которой пересекаются плоскости
DEF и SBC; плоскости FDE и SAC ;
DEF и SBC; плоскости FDE и SAC ;
Пользуясь данным рисунком, назовите:
Слайд 20
а) Две плоскости, cодержащие
прямую DE.
б) Прямую по
которой пересекаются плоскости
АЕF и SBC.
АЕF и SBC.
S
Пользуясь данным рисунком, назовите:
Слайд 21
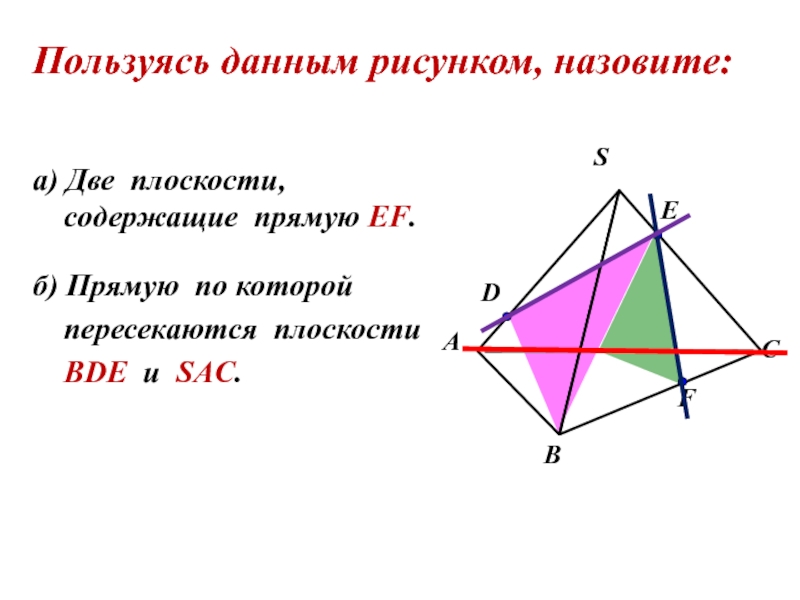
а) Две плоскости,
cодержащие прямую EF.
б) Прямую по которой
пересекаются плоскости
BDЕ и SAC.
BDЕ и SAC.
Пользуясь данным рисунком, назовите:
Слайд 22Теорема 1.Через прямую и не лежащую на ней точку проходит плоскость,
и притом только одна.
Следствия из аксиом.
Слайд 24Доказательство.
Возьмем точки Р a, Q a.По А1 α,
Р α,Q α,М α. Так как Р α и Q α, то по А2 а α.
Любая плоскость, проходящая через прямую а и точку М, проходит через точки М, P, Q. Следовательно, она совпадает с α, так как по А1 через точки M, P, Q проходит только одна плоскость.
Любая плоскость, проходящая через прямую а и точку М, проходит через точки М, P, Q. Следовательно, она совпадает с α, так как по А1 через точки M, P, Q проходит только одна плоскость.
Слайд 27Доказательство
Возьмем точку N b. По Т1 α, а α,N α.
Так как N b,M b и N α, М α,то по А2 b α. Итак, a α и b α.
Любая плоскость, проходящая через a и b, проходит через N. Следовательно, она совпадает с α, так как по T1 через N и a проходит только одна плоскость.
Любая плоскость, проходящая через a и b, проходит через N. Следовательно, она совпадает с α, так как по T1 через N и a проходит только одна плоскость.
