- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайные величины. Распределения случайных величин презентация
Содержание
- 1. Случайные величины. Распределения случайных величин
- 2. Случайная величина Случайная величина – это числовая
- 3. Случайные величины будем обозначать заглавными последними буквами
- 4. Закон распределения случайной величины Любое правило, которое
- 5. Дискретная СВ. Таблица распределения Ряд распределения(может быть
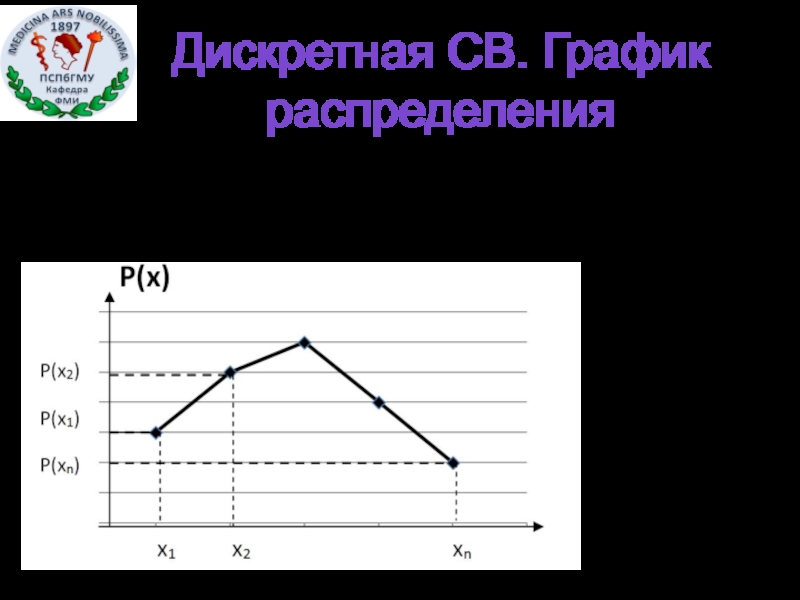
- 6. График: многоугольник распределения. Дискретная СВ. График распределения
- 7. Функция распределения F(x0)– это вероятность того, что
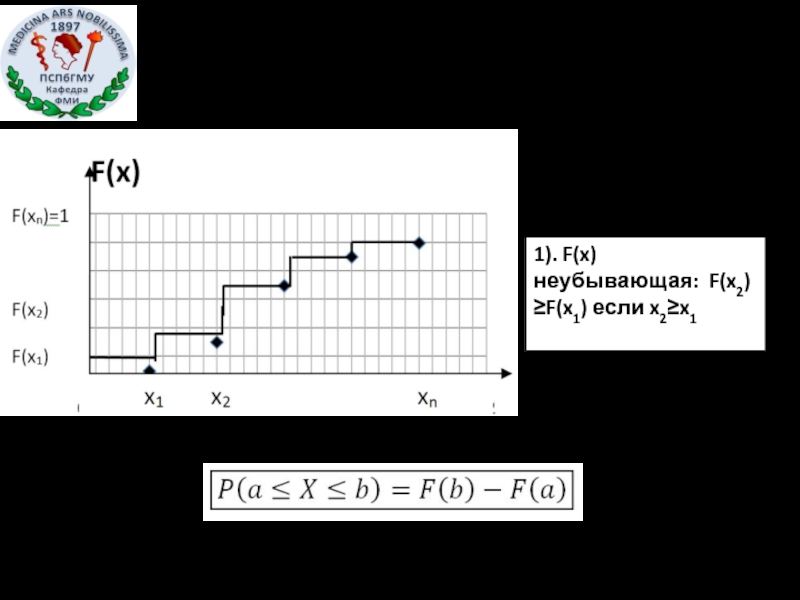
- 8. 1). F(x) неубывающая: F(x2)≥F(x1) если x2≥x1 2).F(-∞)=0; F(+∞)=1
- 9. Пример
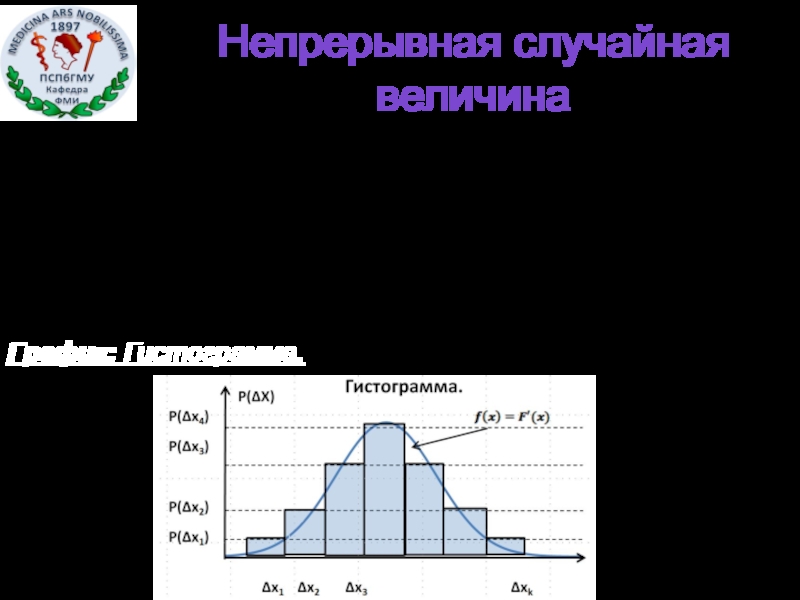
- 10. Непрерывная случайная величина Таблица: Интервальный ряд распределения. График: Гистограмма.
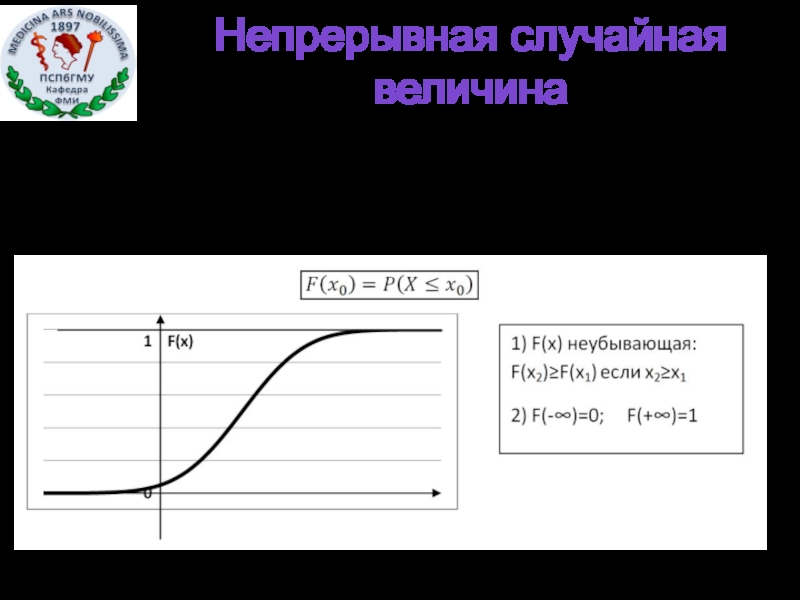
- 11. Функция распределения Непрерывная случайная величина
- 12. Функция плотности распределения f(x): (только для непрерывной случайной величины). Непрерывная случайная величина
- 13. Функция плотности распределения f(x) неотрицательная функция (f(x)≥0)
- 14. Вероятность попадания случайной величины в интервал [a,b]: Функция плотности распределения Условие нормировки:
- 15. Числовые характеристики (параметры) случайной величины Математическое ожидание Дисперсия (рассеивание) Средне-квадратическое или стандартное отклонение
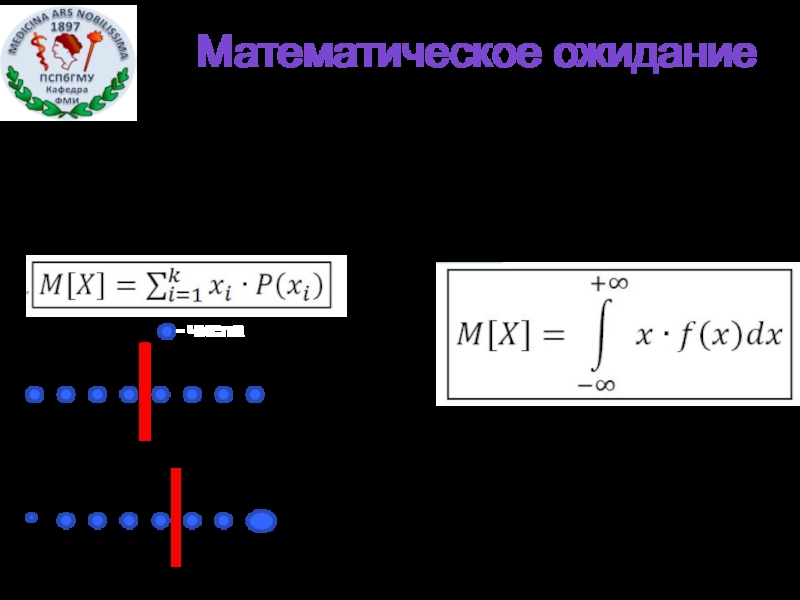
- 16. Математическое ожидание Дискретная случайная величина Непрерывная случайная
- 17. Дисперсия (рассеивание) это математическое ожидание (среднее
- 18. Равномерное или прямоугольное распределение Случайная величина называется
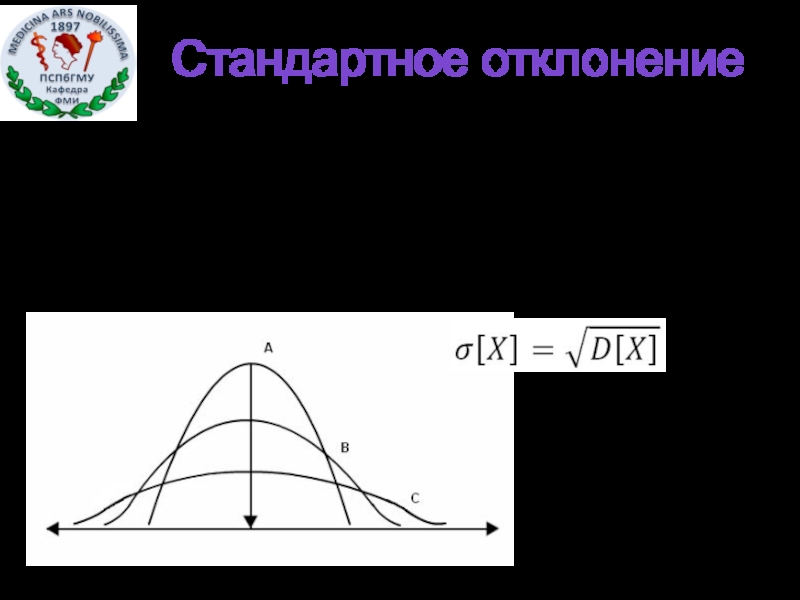
- 19. Стандартное отклонение Средне-квадратическое или стандартное отклонение:
- 20. Равномерное распределение. Чему равна константа Из условия нормировки получаем:
- 21. Равномерное распределение. Вероятность попадания в интервал
- 22. Нормальное распределение или распределение Гаусса Случайная величина
- 23. Нормальное распределение. График плотности распределения Кривая симметрична
- 24. Нормальное распределение. Примеры графиков плотности распределения Графики
- 25. Нормальное распределение. Математическое ожидание и дисперсия Математическое
- 26. Нормальное распределение. Нормированная случайная величина Введем замену
- 27. Нормальное распределение. Нормальная функция распределения Функция распределения
- 28. Значения функции Ф(t) для 0 ≤ t ≤ 3
- 29. Вероятность попадания значений н.р. случайной величины в интервал Правило трёх сигм: Интервал [a;b]
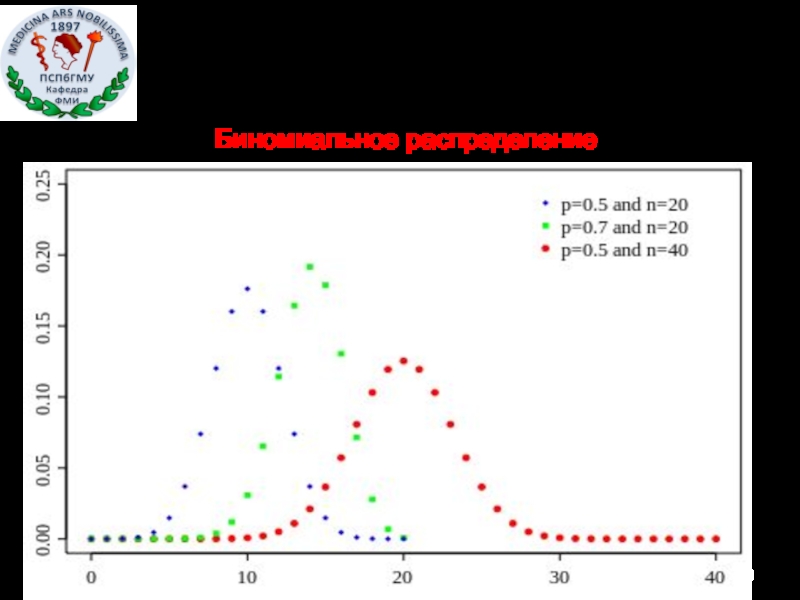
- 30. Биномиальное распределение
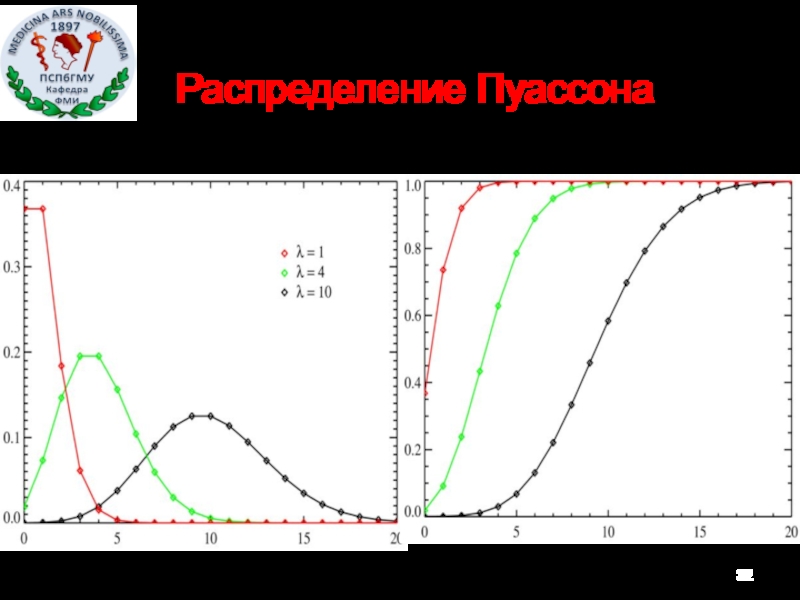
- 32. Распределение Пуассона
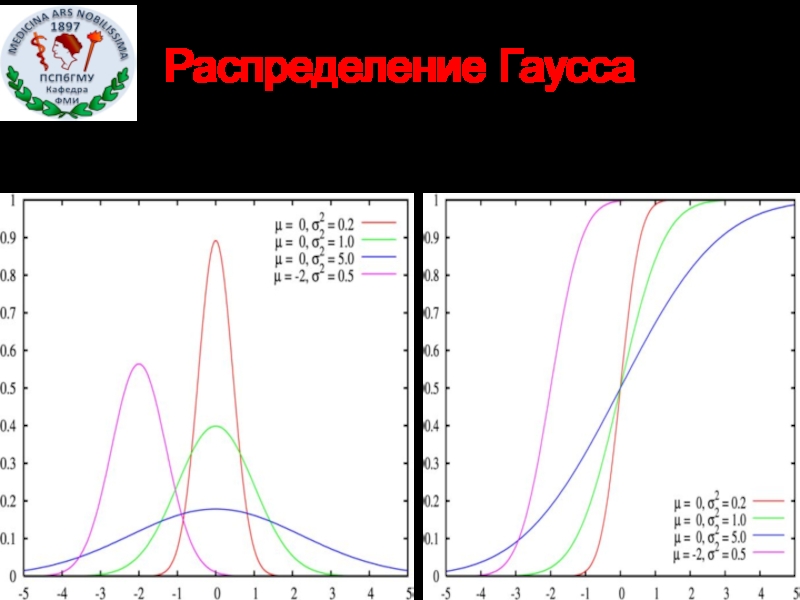
- 34. Распределение Гаусса
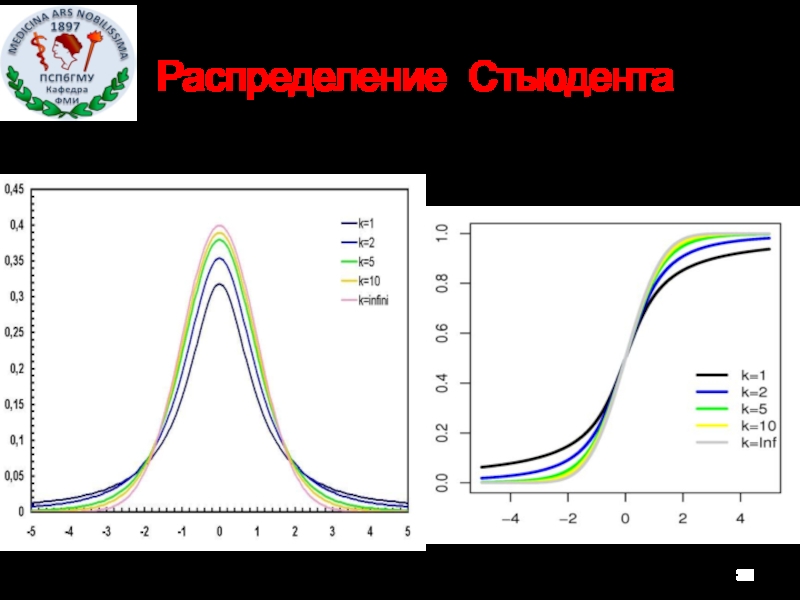
- 36. Распределение Стьюдента
Случайная величина Случайная величина – это числовая переменная, которая принимает свои значения в зависимости от случайных обстоятельств. функция, действующая из вероятностного пространства (множество событий) в множество вещественных чисел. .Дискретная (точечная) СВ
Слайд 1Случайные величины. Распределения случайных величин
Тишков Артем Валерьевич, к.ф.-м.н., доцент
Микрюкова Надежда Николаевна
Слайд 2Случайная величина
Случайная величина – это
числовая переменная, которая принимает свои значения в
зависимости от случайных обстоятельств.
функция, действующая из вероятностного пространства (множество событий) в множество вещественных чисел.
.Дискретная (точечная) СВ принимает отдельные числовые значения (число студентов в аудитории, игральная кость: 1,2,3,4,5,6)
Непрерывная случайная величина принимает любые значения из некоторого интервала (масса тела, рост студентов), возможно бесконечного.
функция, действующая из вероятностного пространства (множество событий) в множество вещественных чисел.
.Дискретная (точечная) СВ принимает отдельные числовые значения (число студентов в аудитории, игральная кость: 1,2,3,4,5,6)
Непрерывная случайная величина принимает любые значения из некоторого интервала (масса тела, рост студентов), возможно бесконечного.
Слайд 3Случайные величины будем обозначать заглавными последними буквами латинского алфавита:X,Y,Z…,а их возможные
значения прописными буквами: X {x1, x2, …,xn}, Y {y1, y2, …,ym}
Любое правило, которое устанавливает связь между возможными значениями случайной величины и вероятностями, с которыми она эти значения принимает, называется законом распределения случайной величины.
Закон распределения СВ можно задавать в виде: 1) таблицы, 2) графика, 3) Функции распределения.
Любое правило, которое устанавливает связь между возможными значениями случайной величины и вероятностями, с которыми она эти значения принимает, называется законом распределения случайной величины.
Закон распределения СВ можно задавать в виде: 1) таблицы, 2) графика, 3) Функции распределения.
Случайная величина
Слайд 4Закон распределения случайной величины
Любое правило, которое устанавливает связь между возможными значениями
случайной величины и вероятностями, с которыми она эти значения принимает, называется законом распределения случайной величины.
Закон распределения случайной величины можно задавать в виде:
1) Таблицы
2) Графика
3) Функции распределения.
Закон распределения случайной величины можно задавать в виде:
1) Таблицы
2) Графика
3) Функции распределения.
Слайд 5Дискретная СВ. Таблица распределения
Ряд распределения(может быть конечным или бесконечным)
Так как события
X=x1, X=x2…. попарно несовместны и составляют полную группу событий, следовательно
Слайд 7 Функция распределения F(x0)– это вероятность того, что случайная величина X принимает
значения меньшие или равные x0.
Дискретная СВ. Функция распределения
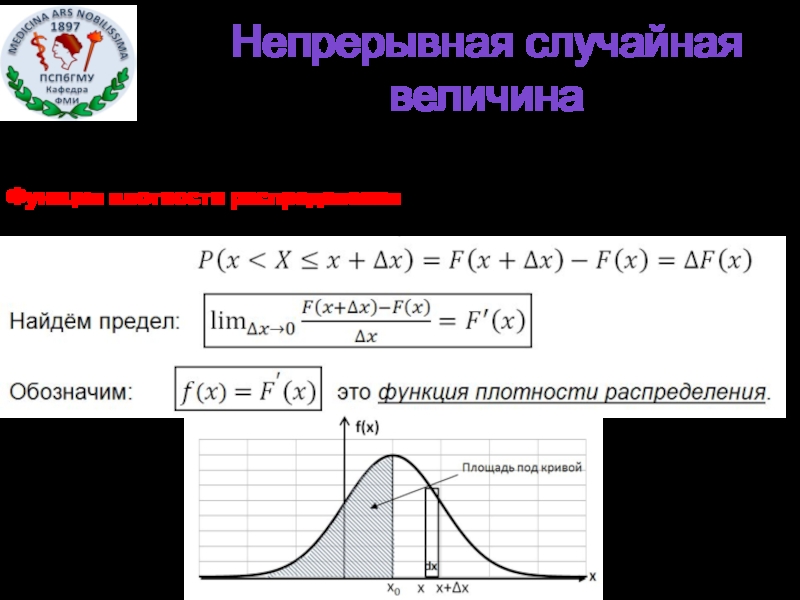
Слайд 12Функция плотности распределения f(x): (только для непрерывной случайной величины).
Непрерывная случайная величина
Слайд 13Функция плотности распределения
f(x) неотрицательная функция (f(x)≥0)
Вероятность попадания в элементарный
интервал dx=(x+Δx)-x
равна f(x)dx=dP.
Слайд 14 Вероятность попадания случайной величины в интервал [a,b]:
Функция плотности распределения
Условие нормировки:
Слайд 15Числовые характеристики (параметры) случайной величины
Математическое ожидание
Дисперсия (рассеивание)
Средне-квадратическое или стандартное отклонение
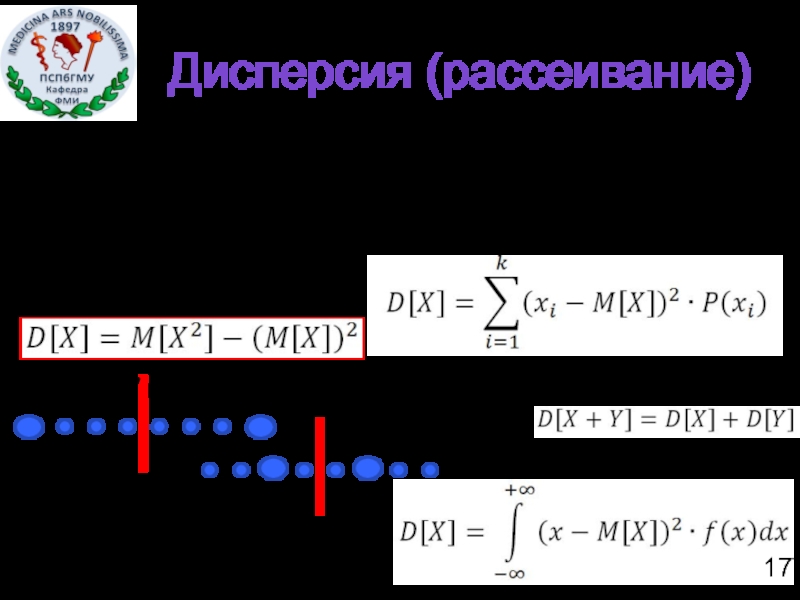
Слайд 17Дисперсия (рассеивание)
это математическое ожидание (среднее значение) квадрата отклонения случайной величины
X от её математического ожидания.
Если X и Y независимые случайные величины, то
Непрерывная случайная величина:
Слайд 18Равномерное или прямоугольное распределение
Случайная величина называется равномерно распределённой на интервале [c,d],
если функция плотности распределения её на этом интервале постоянна, а вне него равна нулю
Слайд 21Равномерное распределение. Вероятность попадания в интервал
f(x)
Каждое значение на отрезке [a;b]
случайная величина принимает с одинаковой вероятностью.
Слайд 22Нормальное распределение или распределение Гаусса
Случайная величина распределена по нормальному закону, если
функция плотности её распределения имеет вид:
где а,σ – параметры распределения.
Слайд 23Нормальное распределение. График плотности распределения
Кривая симметрична относительно прямой х=а
достигается в этой
же точке х=а
На графике представлены вероятности попадания в интервалы среднее значение плюс-минус одна, две и три сигмы
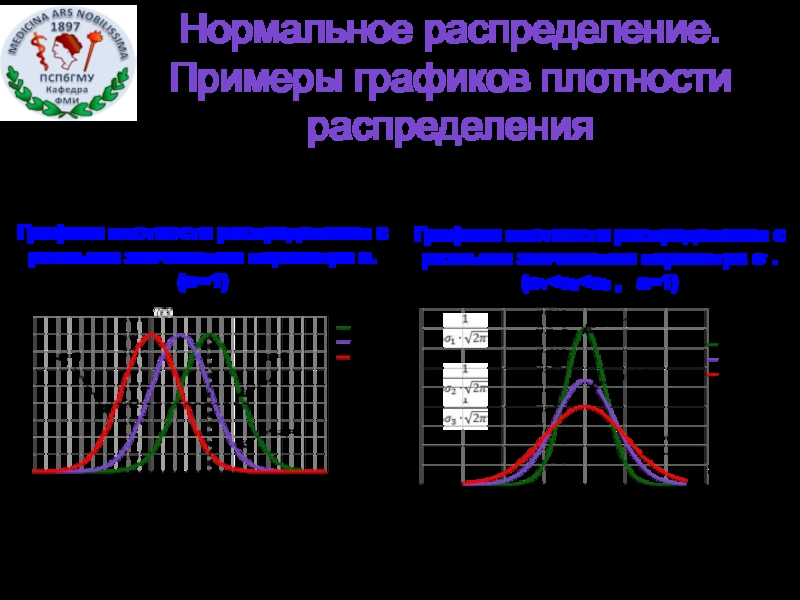
Слайд 24Нормальное распределение. Примеры графиков плотности распределения
Графики плотности распределения с разными значениями
параметра а. (σ=1)
Графики плотности распределения с разными значениями параметра σ . (σ₁<σ₂<σ₃ , a=1)
a3=0
a1=2
a2=1
Слайд 25Нормальное распределение. Математическое ожидание и дисперсия
Математическое ожидание н.р. равно a:
Дисперсия н.р.
равна σ2:
Величину σ называют среднеквадратичным отклонением:
Слайд 26Нормальное распределение. Нормированная случайная величина
Введем замену переменной
t – безразмерная случайная величина.
Важные свойства: М[t]=0 D[t]=1 σ[t] =1
Так как 99,7% всех значений случайной величины Х отличаются от М[Х] не больше, чем на 3·σ[Х], следовательно для любого значения x получим:
с вероятностью Р=0,997.
Слайд 27Нормальное распределение. Нормальная функция распределения
Функция распределения н.р.
Введем замену переменной
Ф(t) называется функцией
Гаусса или нормальной функцией распределения
Слайд 29Вероятность попадания значений н.р. случайной величины в интервал
Правило трёх сигм:
Интервал
[a;b]
