- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайные величины (лекция 4) презентация
Содержание
- 1. Случайные величины (лекция 4)
- 2. Задача о счастливом билете
- 3. Задача о счастливом билете k=9
- 4. Длина половины номера
- 5. Числовые характеристики дискретной случайной величины Неслучайная (постоянная величина)
- 6. Формула для вычисления дисперсии const const
- 7. Свойства дисперсии
- 8. Дисперсия числа появлений событий в независимых испытаниях
- 9. Среднее квадратическое отклонение сигма
- 10. От дискретности – к непрерывности!
- 11. Плотность распределения вероятностей с.в. (только для непрерывных!) Плотность распределения Функция распределения
- 12. Законы распределения н.с.в. Функция распределения F(x)
- 13. Законы распределения н.с.в. Функция распределения F(x)
- 14. Ещё о нормальном распределении Правило одной сигмы:
- 15. Законы распределения н.с.в. Функция распределения F(x)
- 16. Законы распределения н.с.в. Функция распределения F(x)
- 17. Законы распределения н.с.в. Функция распределения F(x) Плотность распределения f(x)
- 18. Резюме
Слайд 1Математические методы в биологии
Блок 2. Случайные величины
Лекция 4
Козлова Ольга Сергеевна
89276755130, olga-sphinx@yandex.ru
Слайд 8Дисперсия числа появлений событий в независимых испытаниях
n независимых испытаний
Событие A появляется
в каждом из них с вероятностью p
Дискретная случайная величина X – число появления события A в этих испытаниях
ВОПРОС: Чему равна дисперсия случайной величины X - числа появлений события A в испытаниях?
ОТВЕТ: Дисперсия числа появлений события A в n испытаниях равно произведению n на p на (1-p): D(X)=n*p*(1-p)
Доказательство: Пусть X1 – число появления события A в первом испытании, X2 – во втором и.т.д, Xn – в n-ом. Всего событие A появилось X1+X2+…+Xn раз. По свойству дисперсии суммы, D(X)=D(X1)+D(X2)+…+D(Xn).
Распишем D(X1), D(X2),…D(Xn): D(X1)=M(X12)-(M(X1))2
Дискретная случайная величина X12 (как и X1) принимает значение 1 с вероятностью p (событие случилось) и значение 0 с вероятностью (1-p) (событие не случилось). Поэтому D(X1)=1*p+0*(1-p)-(1*p+0*(1-p))2=p-p2=p(1-p). И так для каждого n, поэтому D(X)=n*p*(1-p).
Данная случайная величина X распределена по биномиальному закону, поэтому можно сказать, что
ДИСПЕРСИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПАРАМЕТРАМИ N И P РАВНА ПРОИЗВЕДЕНИЮ N*P*(1-P).
Дискретная случайная величина X – число появления события A в этих испытаниях
ВОПРОС: Чему равна дисперсия случайной величины X - числа появлений события A в испытаниях?
ОТВЕТ: Дисперсия числа появлений события A в n испытаниях равно произведению n на p на (1-p): D(X)=n*p*(1-p)
Доказательство: Пусть X1 – число появления события A в первом испытании, X2 – во втором и.т.д, Xn – в n-ом. Всего событие A появилось X1+X2+…+Xn раз. По свойству дисперсии суммы, D(X)=D(X1)+D(X2)+…+D(Xn).
Распишем D(X1), D(X2),…D(Xn): D(X1)=M(X12)-(M(X1))2
Дискретная случайная величина X12 (как и X1) принимает значение 1 с вероятностью p (событие случилось) и значение 0 с вероятностью (1-p) (событие не случилось). Поэтому D(X1)=1*p+0*(1-p)-(1*p+0*(1-p))2=p-p2=p(1-p). И так для каждого n, поэтому D(X)=n*p*(1-p).
Данная случайная величина X распределена по биномиальному закону, поэтому можно сказать, что
ДИСПЕРСИЯ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПАРАМЕТРАМИ N И P РАВНА ПРОИЗВЕДЕНИЮ N*P*(1-P).
Слайд 9Среднее квадратическое отклонение
сигма
Ответ. Данная случайная величина X имеет мат.ожидание 6,4, дисперсию
13,04 и среднее квадратическое отклонение 3,61.
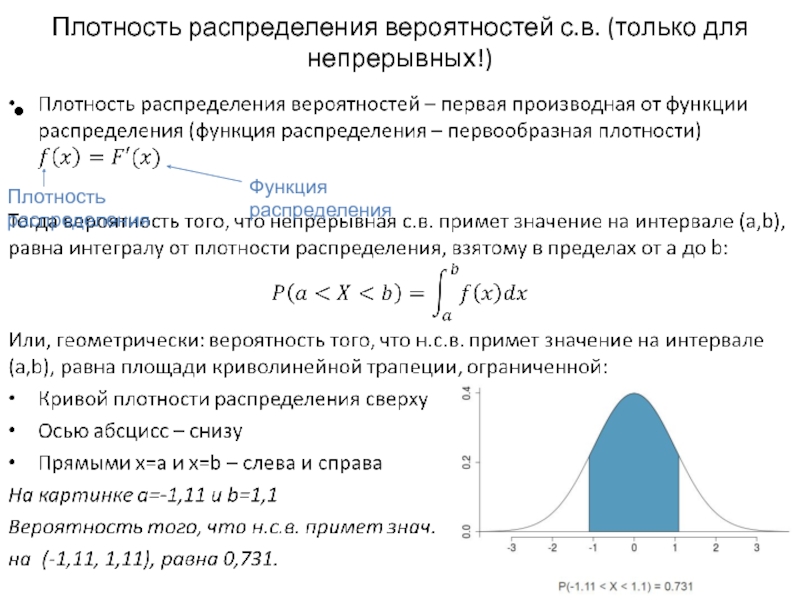
Слайд 11Плотность распределения вероятностей с.в. (только для непрерывных!)
Плотность распределения
Функция распределения
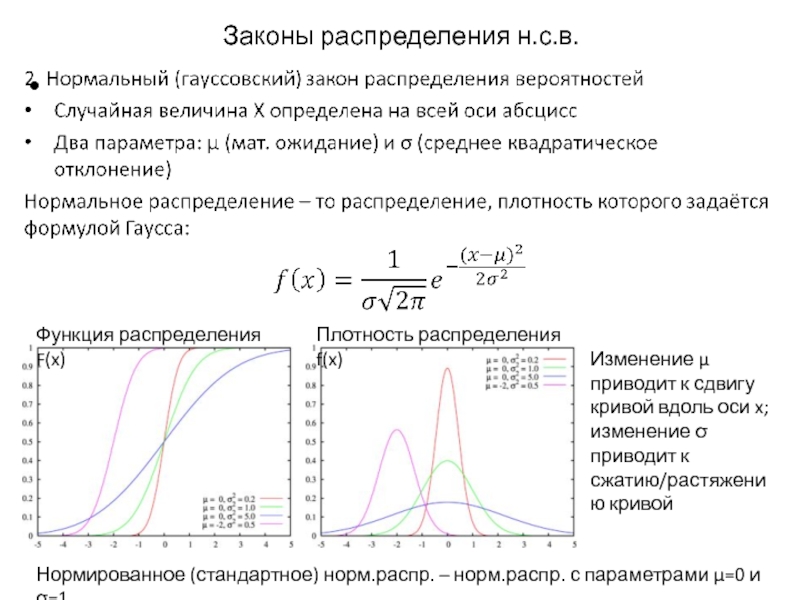
Слайд 12Законы распределения н.с.в.
Функция распределения F(x)
Плотность распределения f(x)
Первая производная линейной функции –
константа!
Слайд 13
Законы распределения н.с.в.
Функция распределения F(x)
Плотность распределения f(x)
Изменение μ приводит к сдвигу
кривой вдоль оси x;
изменение σ приводит к сжатию/растяжению кривой
изменение σ приводит к сжатию/растяжению кривой
Нормированное (стандартное) норм.распр. – норм.распр. с параметрами μ=0 и σ=1
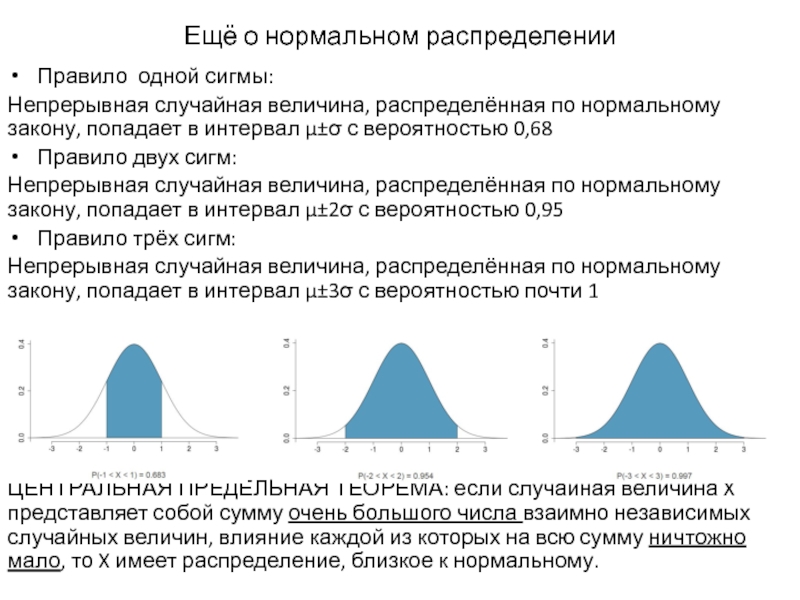
Слайд 14Ещё о нормальном распределении
Правило одной сигмы:
Непрерывная случайная величина, распределённая по нормальному
закону, попадает в интервал μ±σ с вероятностью 0,68
Правило двух сигм:
Непрерывная случайная величина, распределённая по нормальному закону, попадает в интервал μ±2σ с вероятностью 0,95
Правило трёх сигм:
Непрерывная случайная величина, распределённая по нормальному закону, попадает в интервал μ±3σ с вероятностью почти 1
ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
Правило двух сигм:
Непрерывная случайная величина, распределённая по нормальному закону, попадает в интервал μ±2σ с вероятностью 0,95
Правило трёх сигм:
Непрерывная случайная величина, распределённая по нормальному закону, попадает в интервал μ±3σ с вероятностью почти 1
ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.
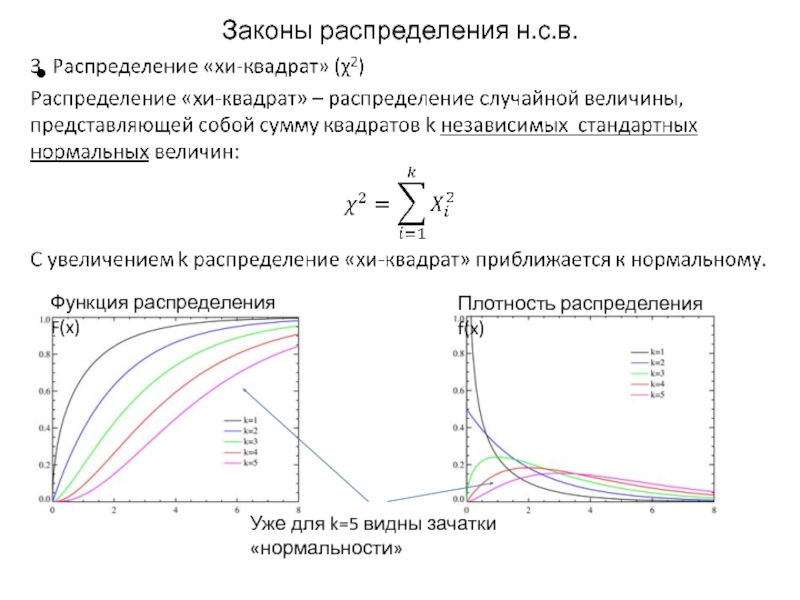
Слайд 15
Законы распределения н.с.в.
Функция распределения F(x)
Плотность распределения f(x)
Уже для k=5 видны зачатки
«нормальности»
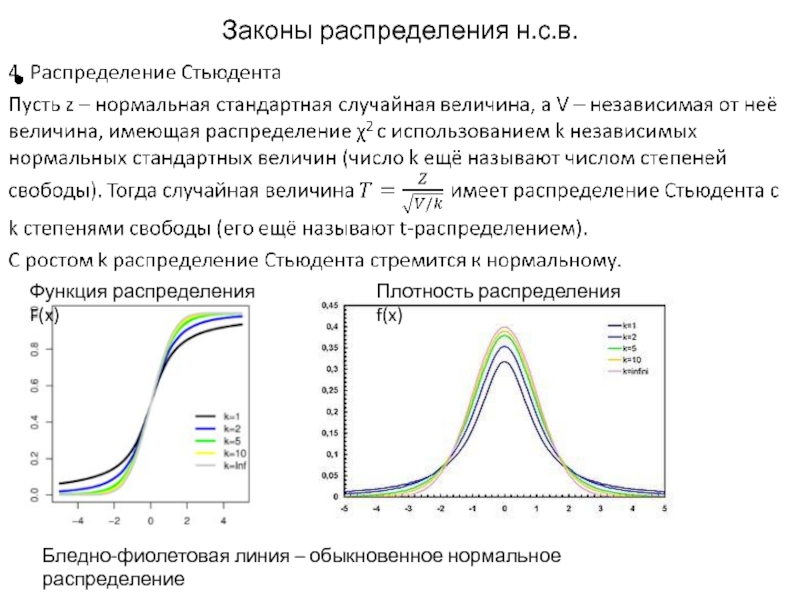
Слайд 16
Законы распределения н.с.в.
Функция распределения F(x)
Плотность распределения f(x)
Бледно-фиолетовая линия – обыкновенное нормальное
распределение