- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площадь многоугольника презентация
Содержание
- 1. Площадь многоугольника
- 2. Цели обучения / lesson objective 8.3.3.9 знать
- 3. Критерии успеха/Success Criteria – знает понятие
- 4. Понятие площади В жизни часто приходится вычислять
- 5. ПЛОЩАДЬ – это… некая величина, характеризующая геометрическую
- 6. Площадь многоугольника Площадь многоугольника – это величина
- 7. Свойства площадей Свойство 1. Равные многоугольники имеют
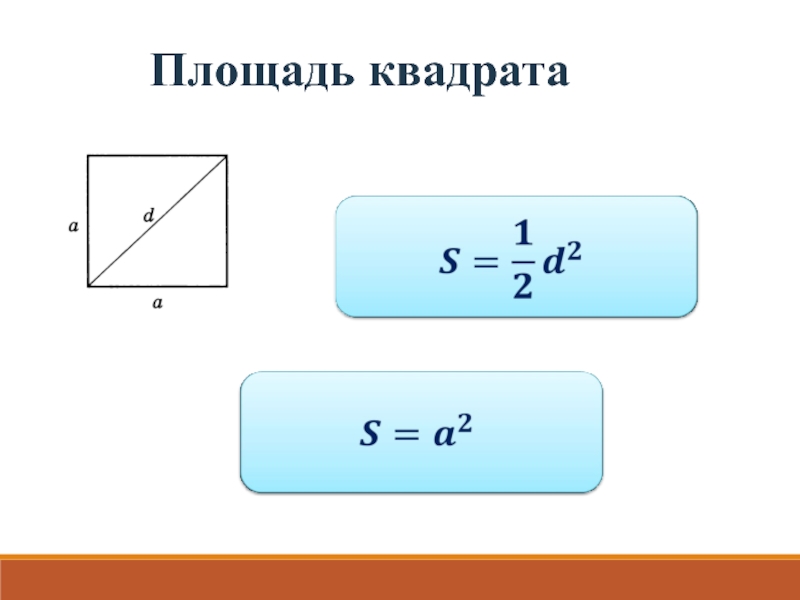
- 8. Площадь квадрата
- 9. b S = ab ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
- 10. B А D C H
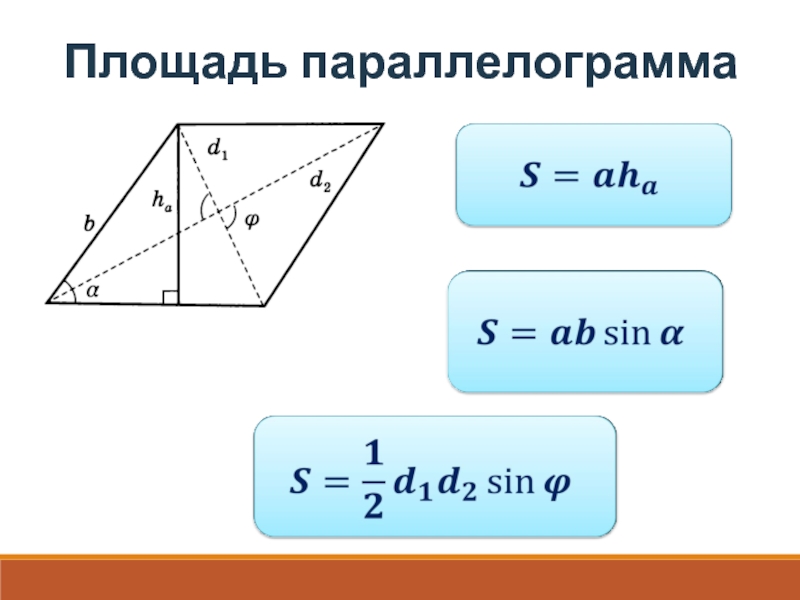
- 11. Площадь параллелограмма
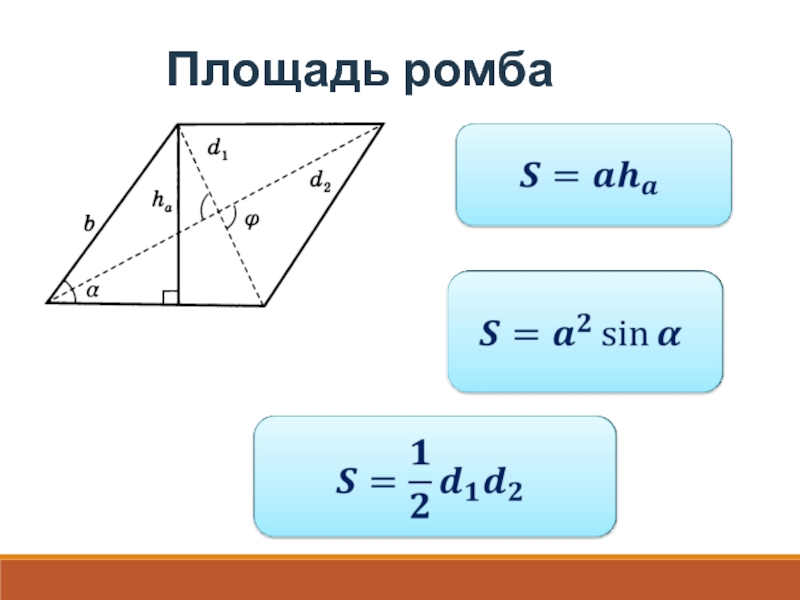
- 12. Площадь ромба
- 13. Решите задачи по готовым чертежам
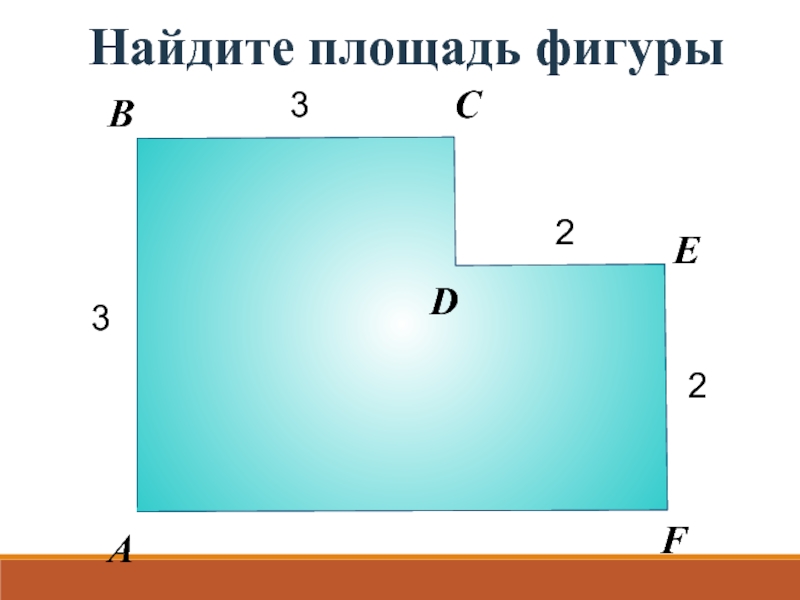
- 14. Найдите площадь фигуры
- 15. Решите задачи 1. Найти площадь ромба, если
- 16. Question 1 Решение задач на английском языке
- 17. Работа в парах/ Work in pairs
- 18. 1) Стороны квадратов относятся как 2:3. Сумма
- 19. 4) Периметр параллелограмма равен 2 дм 8
- 20. Рефлексия
- 21. Домашняя работа/Home Work 1) Найдите периметр прямоугольника,
Слайд 1Понятие площади.
Площадь четырехугольников.
The concept of space.
Area quadrangles.
ТЕМА УРОКА/LESSON THEME
Слайд 2Цели обучения / lesson objective
8.3.3.9
знать понятие площади многоугольника и ее свойства;
8.3.3.10
знать
8.3.3.11
выводить и применять формулы площади параллелограмма, ромба;
Слайд 3Критерии успеха/Success Criteria
– знает понятие площади многоугольника;
– знает свойства площади многоугольника;
–
– применяет формулу площади четырехугольника (квадрат, прямоугольник, параллелограмм, ромб)
Учащийся достиг цели обучения, если:
Слайд 4Понятие площади
В жизни часто приходится вычислять площади геометрических фигур.
Например, приходится определять
При всяком измерении необходимо заранее иметь меру, с которой сравнивается измеряемая величина. При взвешивании употребляются меры веса: килограмм, грамм, тонна, центнер. Время измеряется часами, минутами, секундами.
При измерении длины отрезка МN сравниваем его с метром, сантиметром или с какой-нибудь другой мерой длины. При измерении углов пользуемся угловыми градусами, минутами.
Точно так же при измерении площадей геометрических фигур пользуются особыми мерами, с которыми сравниваются эти фигуры.
Слайд 5ПЛОЩАДЬ – это…
некая величина, характеризующая геометрическую фигуру, расположенную на плоскости или
Обычно площадь обозначается буквой S.
Измерить площадь какой-нибудь геометрической фигуры — значит узнать, сколько тех или иных квадратных единиц содержится в фигуре, площадь которой измеряется.
Слайд 6Площадь многоугольника
Площадь многоугольника – это величина той части площади, которую занимает
Площадь многоугольника – выражается положительным числом
Площадь многоугольника показывает сколько раз единица измерения или её части укладываются в данном многоугольнике.
Слайд 7Свойства площадей
Свойство 1. Равные многоугольники имеют равные площади
Многоугольники, имеющие равные площади
Свойство 2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Если многоугольник разрезан на несколько многоугольников и из него составлен другой многоугольник, то такие многоугольники называют равносоставленными.
Свойство 3. Площадь квадрата равна квадрату его стороны.
М
F
Слайд 9
b
S = ab
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА РАВНА ПРОИЗВЕДЕНИЮ ЕГО СМЕЖНЫХ СТОРОН
a
S
S = ab
a
a
a
b
b
b
a2
S
b2
(a+b)2
(a+b)2
a2+2ab+ b2= 2S+a2+b2
Слайд 10
B
А
D
C
H
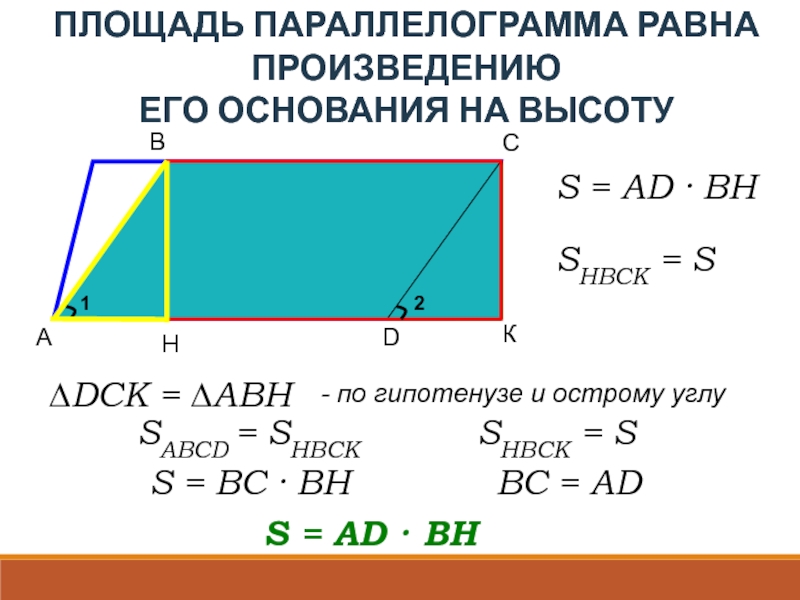
ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА РАВНА ПРОИЗВЕДЕНИЮ
ЕГО ОСНОВАНИЯ НА ВЫСОТУ
S = AD ·
К
S
SHBCK = S
∆DCK = ∆ABH
- по гипотенузе и острому углу
1
2
SABCD = SHBCK
SHBCK = S
S = BC · BH
BC = AD
S = AD · BH
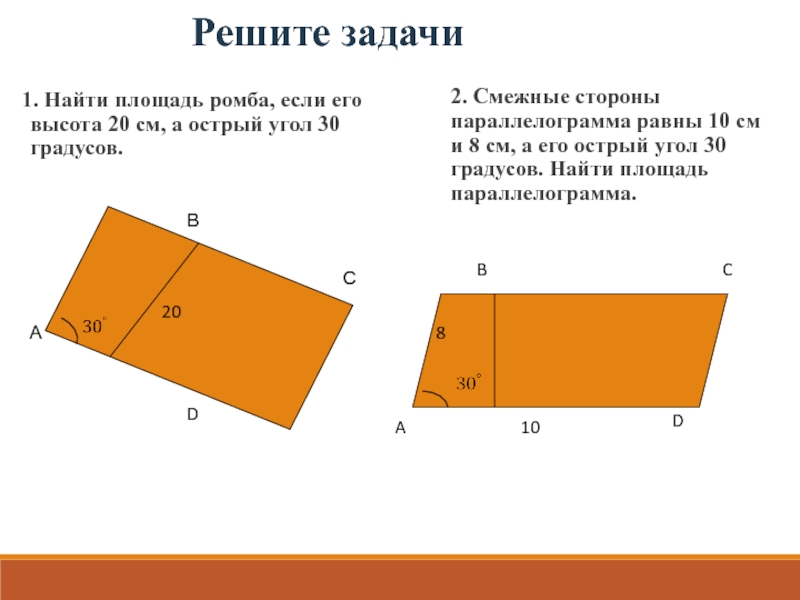
Слайд 15Решите задачи
1. Найти площадь ромба, если его высота 20 см, а
2. Смежные стороны
параллелограмма равны 10 см
и 8 см, а его острый угол 30
градусов. Найти площадь
параллелограмма.
20
А
В
С
D
A
B
C
D
8
10
Слайд 16Question 1
Решение задач на английском языке
A paper kite in a rhombus
The small diagonal is 15 in and the large diagonal is 48 in.
How much paper was used to make the kite? (Use the diagram below as needed.)
Слайд 181) Стороны квадратов относятся как 2:3. Сумма их площадей равна 117
3) Длина диагонали квадрата равна 4 см. Найдите периметр квадрата.
2) Стороны прямоугольника равны см и см.
Площадь некоторого квадрата на 4 кв.см больше площади данного прямоугольника. Найдите длину стороны квадрата.
Слайд 194) Периметр параллелограмма равен 2 дм 8 см; высоты, проведенные из
5) Одна из диагоналей ромба на 6 мм меньше другой диагонали. Найдите длины этих диагоналей, если площадь ромба равна 0,2 кв.см.
Слайд 21Домашняя работа/Home Work
1) Найдите периметр прямоугольника, если одна из его сторон
2) Острый угол параллелограмма равен 30°. Периметр параллелограмма равен 4 дм. Отношение длин смежных сторон равно 2:3. Найдите площадь параллелограмма.
3) Одна из диагоналей ромба в четыре раза больше другой диагонали. Найдите длины этих диагоналей, если площадь ромба равна 72 кв.см.