Лекция 3. Случайная величина. Закон распределения случайной величины. Числовые характерис-тики случайной величины.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайная величина. Закон распределения случайной величины. Числовые характеристики случайной величины презентация
Содержание
- 1. Случайная величина. Закон распределения случайной величины. Числовые характеристики случайной величины
- 2. Случайная величина
- 3. Закон распределения случайной величины
- 4. Закон распределения случайной величины Закон распределения дискретной
- 5. Закон распределения случайной величины Дискретная случайная величина
- 6. Закон распределения случайной величины Гистограмма распределения дискретной
- 7. Закон распределения случайной величины
- 8. Закон распределения случайной величины Функций распределения случайной
- 9. Биномиальное распределение Биномиальное распределение - это распределение
- 10. Распределение Пуассона Распределение Пуассона - это распределение
- 11. Распределение Пуассона С помощью формулы Пуассона можно
- 12. Нормальное распределение (распределение Гаусса) Случайная величина называется
- 13. Равномерное распределение Случайная величина называется равномерно распределённой
Слайд 1СТАТИСТИКА
Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
Введение в
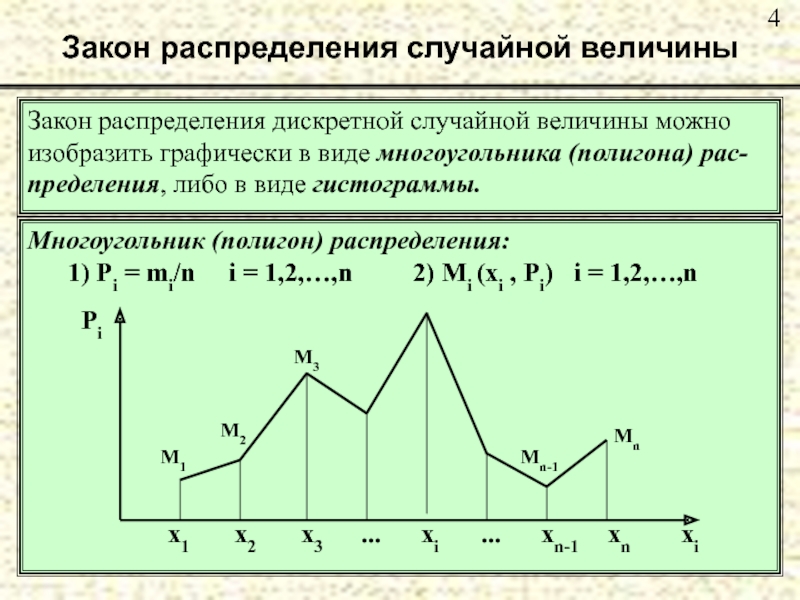
Слайд 4Закон распределения случайной величины
Закон распределения дискретной случайной величины можно
изобразить графически
пределения, либо в виде гистограммы.
Многоугольник (полигон) распределения:
1) Pi = mi/n i = 1,2,…,n 2) Mi (xi , Pi) i = 1,2,…,n
Pi
xi
xn-1
xi
x3
x2
x1
...
...
xn
M1
M2
M3
Mn-1
Mn
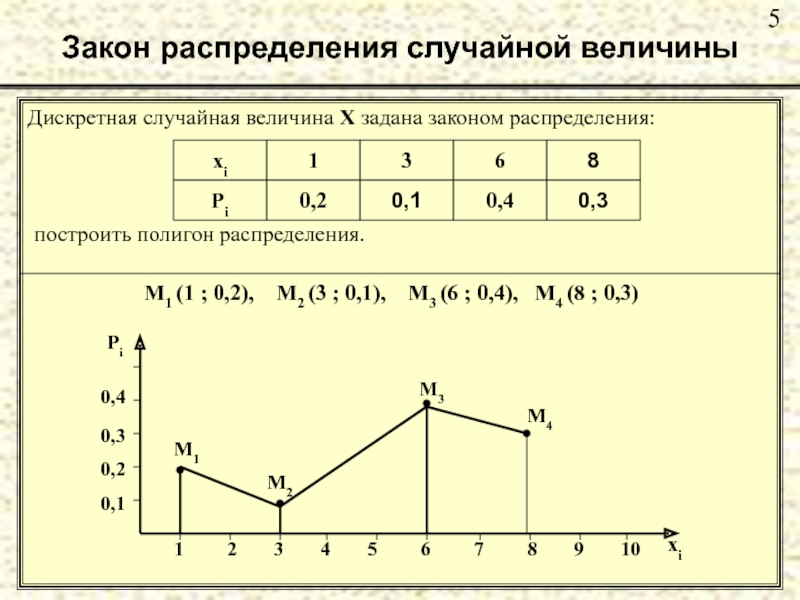
Слайд 5Закон распределения случайной величины
Дискретная случайная величина Х задана законом распределения:
построить
M1 (1 ; 0,2), M2 (3 ; 0,1), M3 (6 ; 0,4), M4 (8 ; 0,3)
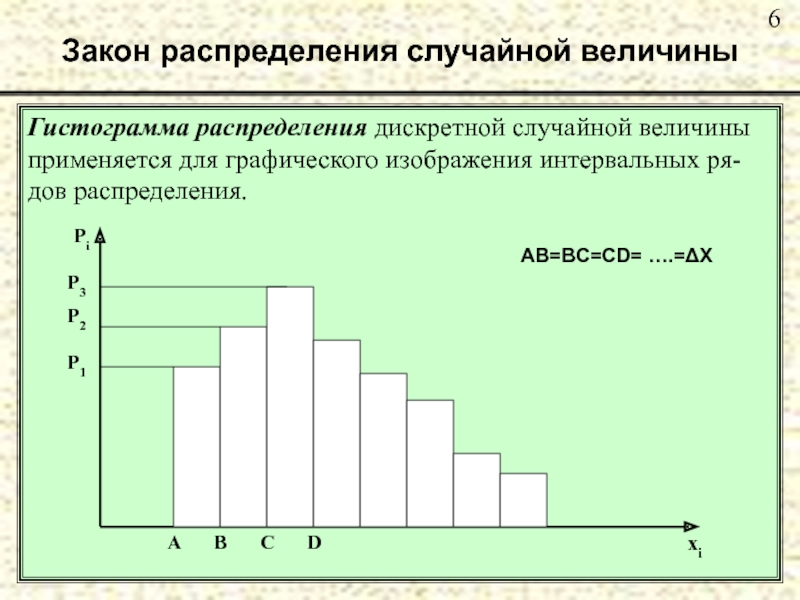
Слайд 6Закон распределения случайной величины
Гистограмма распределения дискретной случайной величины
применяется для графического изображения
дов распределения.
Pi
xi
P1
P2
А
В
С
D
P3
AB=BC=CD= ….=ΔX
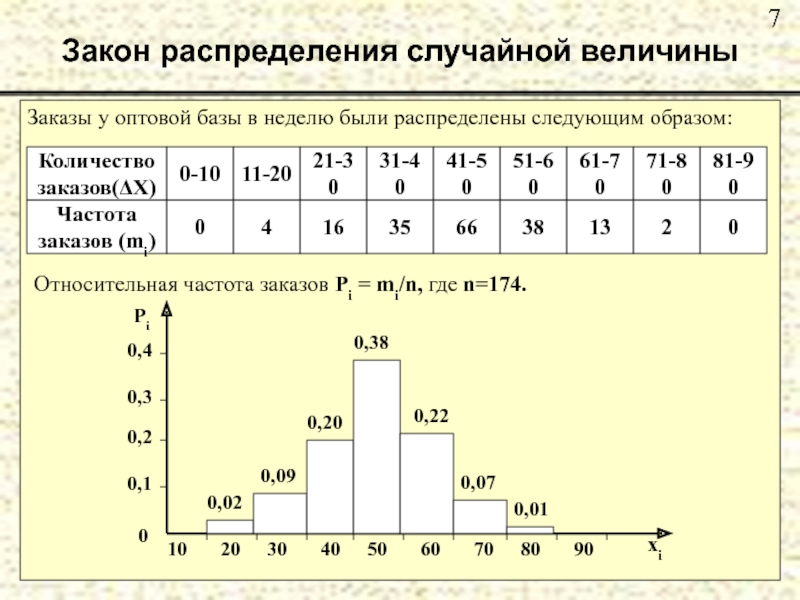
Слайд 8Закон распределения случайной величины
Функций распределения случайной величины на сегодняшний
день выявлено
значительно меньшим числом. Среди наиболее употребляемых
следует отметить следующие: биномиальное, распределение
Пуассона, нормальное и равномерное распределение случай-
ной величины.
В теории вероятности случайная величина полностью характе-
ризуется своей функцией распределения. При помощи функции
(закона) распределения можно оценить вероятность того, что
случайная величина попадет в заданный интервал [а,b].
P(а ≤ X
Слайд 9Биномиальное распределение
Биномиальное распределение - это распределение случайных
величин, в котором может быть
ный и неблогоприятный. Если известна вероятность успеха p в
каждом испытании, то вероятность k удачных исходов в n ре-
реализациях (наблюдениях) равна:
Геометрическое распределение - частный случай биномиального
распределения; при k=1 оно описывает вероятность первого удач-
ного результата во всех n реализациях (испытаниях):
Слайд 10Распределение Пуассона
Распределение Пуассона - это распределение числа появления
редких случайных событий, которые
противоположных значения. Это распределение возникает, когда
вероятность наступления одного из признаков мала, а число ис-
пытаний n большое. Если известна вероятность успеха p в
каждом испытании, то вероятность того, что в n независимых ис-
пытаниях событие наступит k раз, равна:
a - параметр распределения; a = n * p
Слайд 11Распределение Пуассона
С помощью формулы Пуассона можно найти вероятность появ-
ления однородных событий,
мени. Вероятность того, что величина интервала между соседни-
ми событиями (например между включением оборудования и его
отказом) не превосходит t, равна:
Вероятность безотказной работы:
t = 1,2,3,….
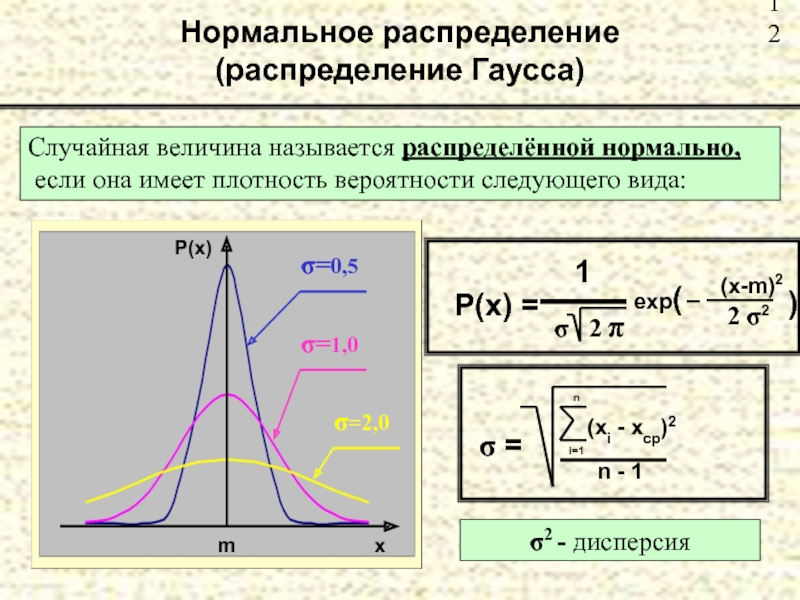
Слайд 12Нормальное распределение
(распределение Гаусса)
Случайная величина называется распределённой нормально,
если она имеет плотность
σ 2
2 σ2
)
σ =
(xi - xср)2
i=1
n
n - 1
σ2 - дисперсия
Слайд 13Равномерное распределение
Случайная величина называется равномерно распределённой
на [a,b], если её плотность вероятности
янна, а вне [a,b] равна 0.
b
a







![Равномерное распределениеСлучайная величина называется равномерно распределённойна [a,b], если её плотность вероятности на этом интервале посто-янна,](/img/tmb/4/337716/934d4f559f3a3d2de8b41a145eae6c8e-800x.jpg)





