Сложная функция презентация

Содержание

1. Сложная функция
2. Содержание Введение понятия сложной функции Примеры
3. Определение функции
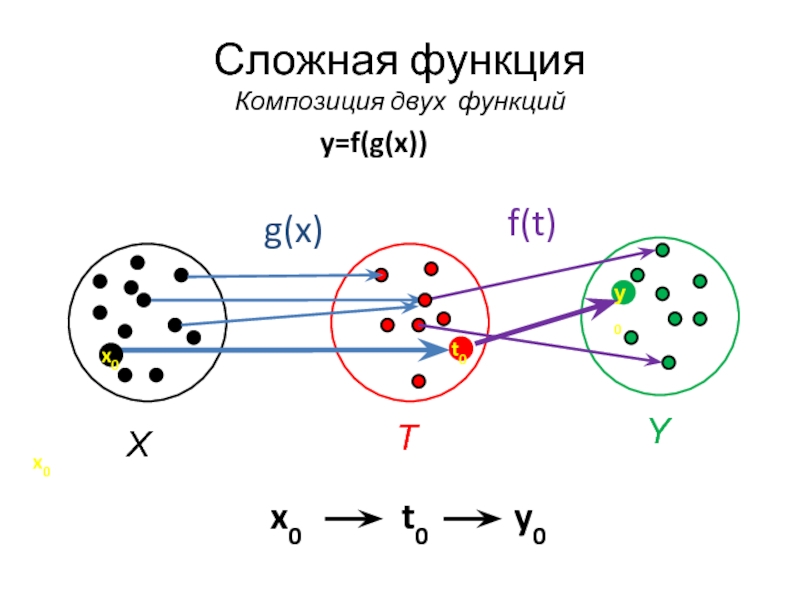
4. Сложная функция Композиция двух функций y=f(g(x))
5. Формула для задания сложной функции
6. Примеры сложных функций 1.
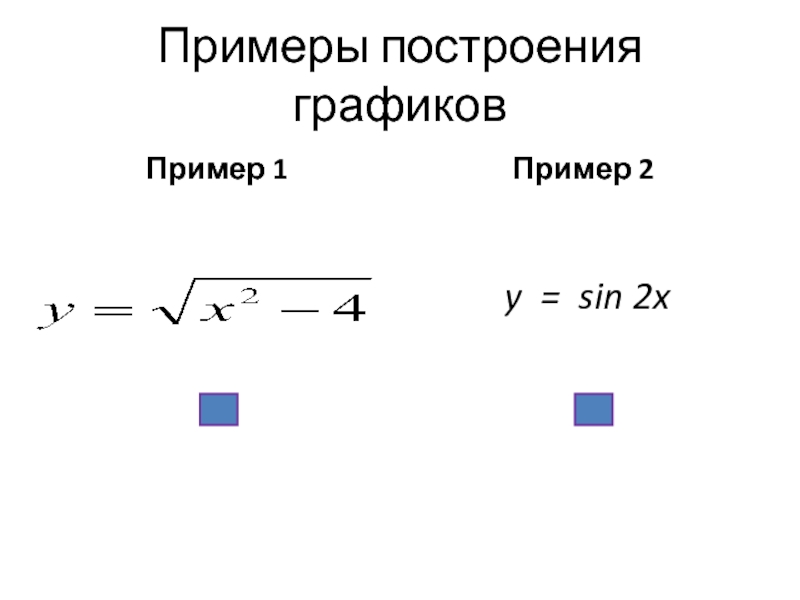
7. Примеры построения графиков Пример 1 Пример 2
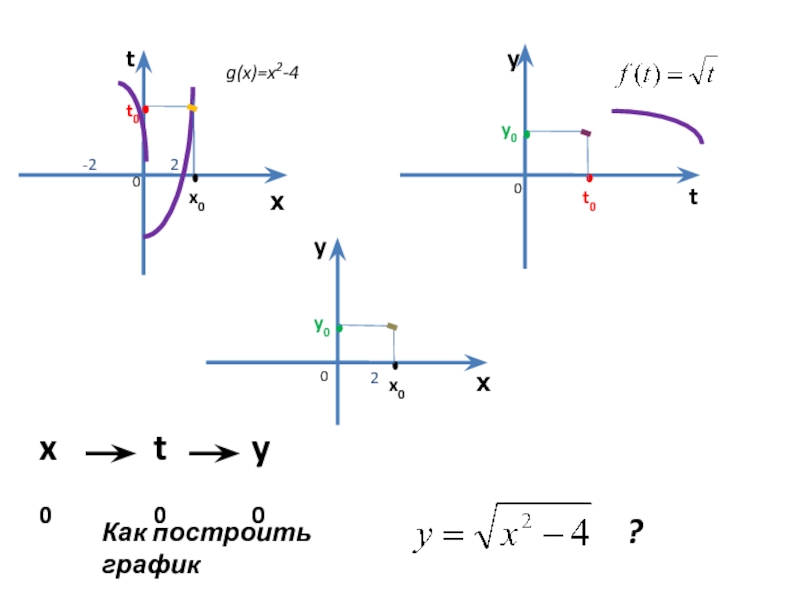
8. Пример 1 1. Найдем область определения функции:
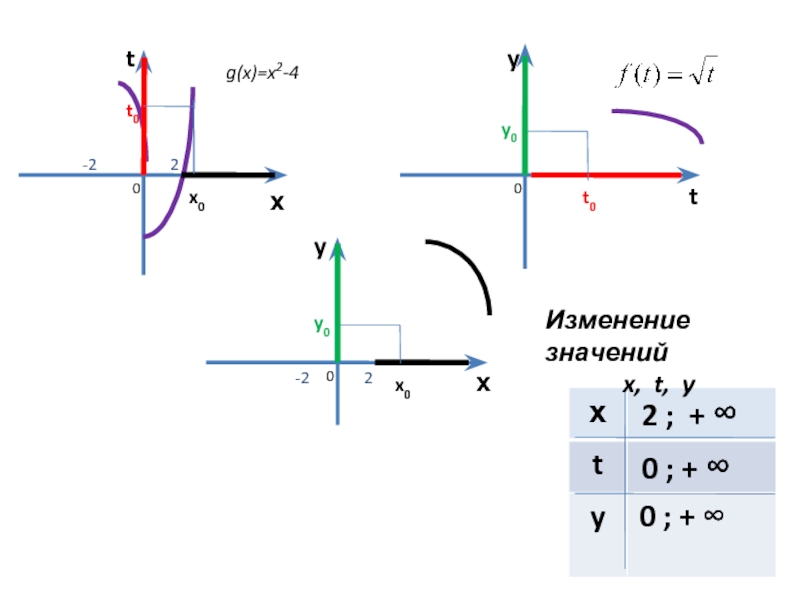
9. х t х y y
10. х t х y
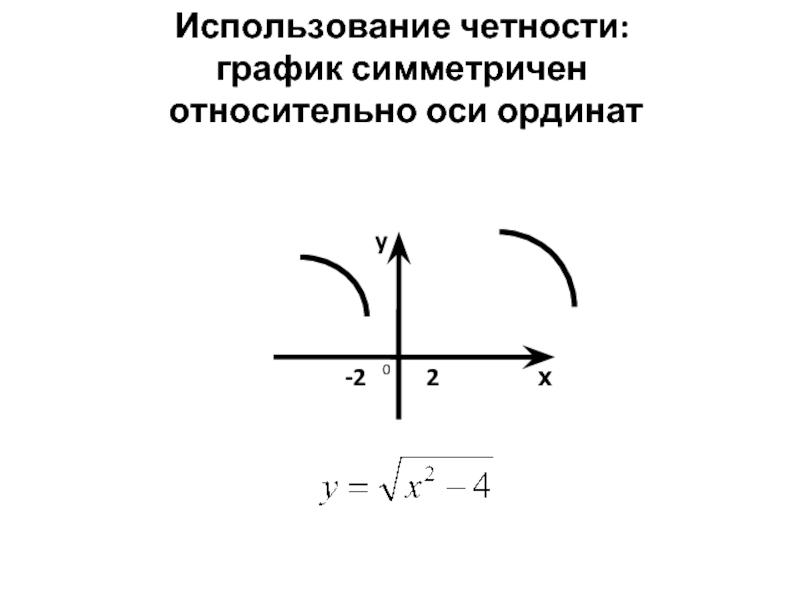
11. 0 Использование четности: график симметричен
12. Пример 2 1. D(y) = R
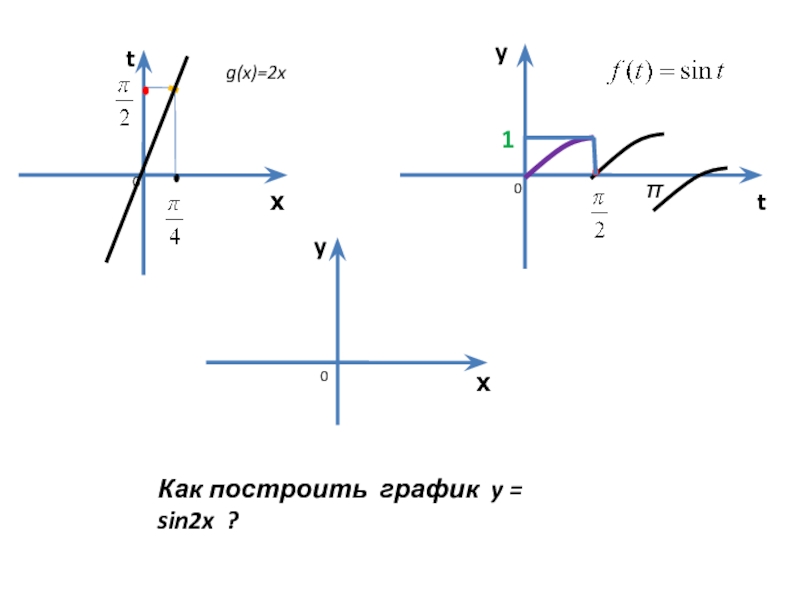
13. х t х y y t g(x)=2x
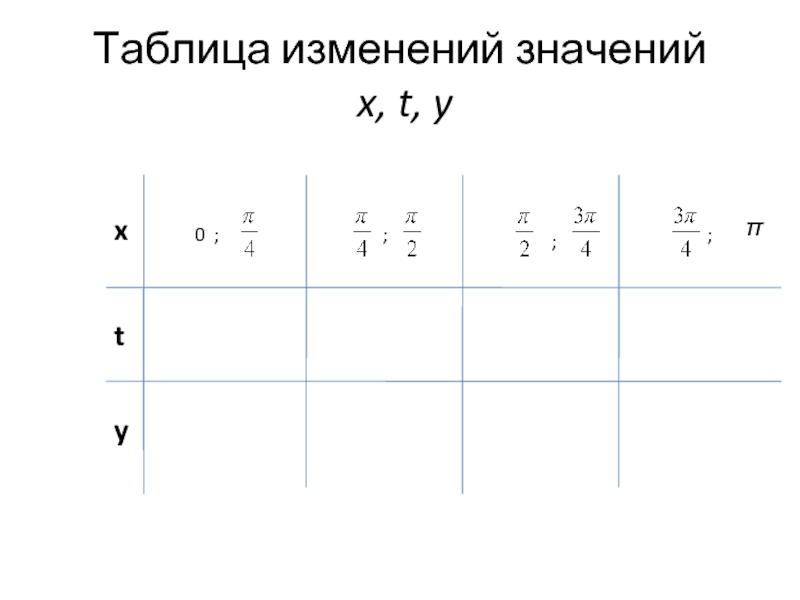
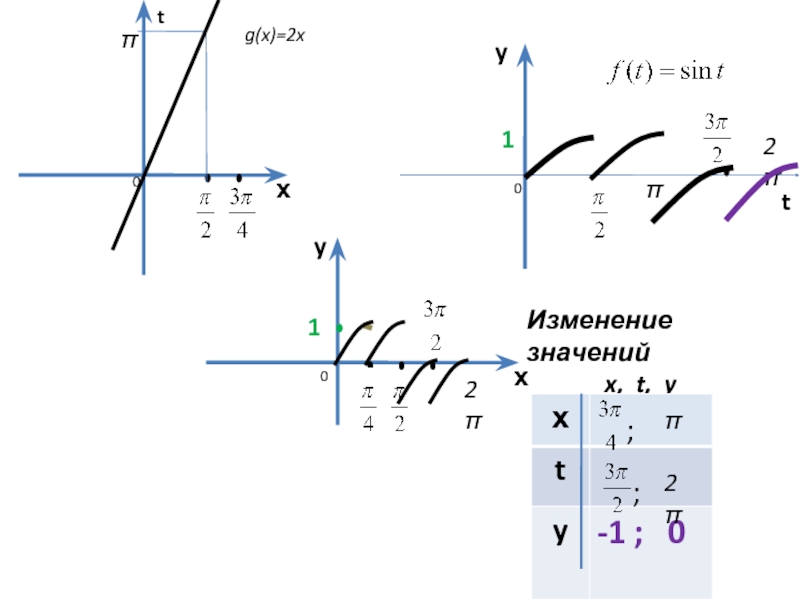
14. Таблица изменений значений x, t, y
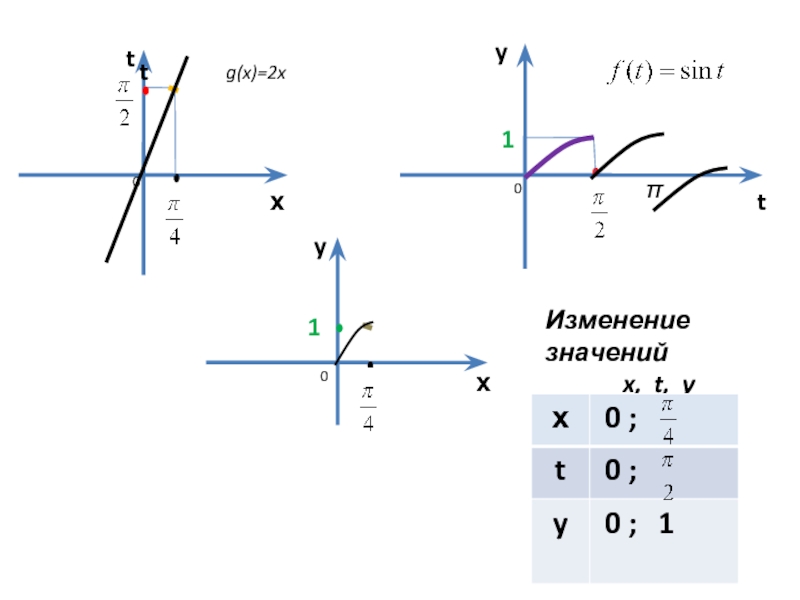
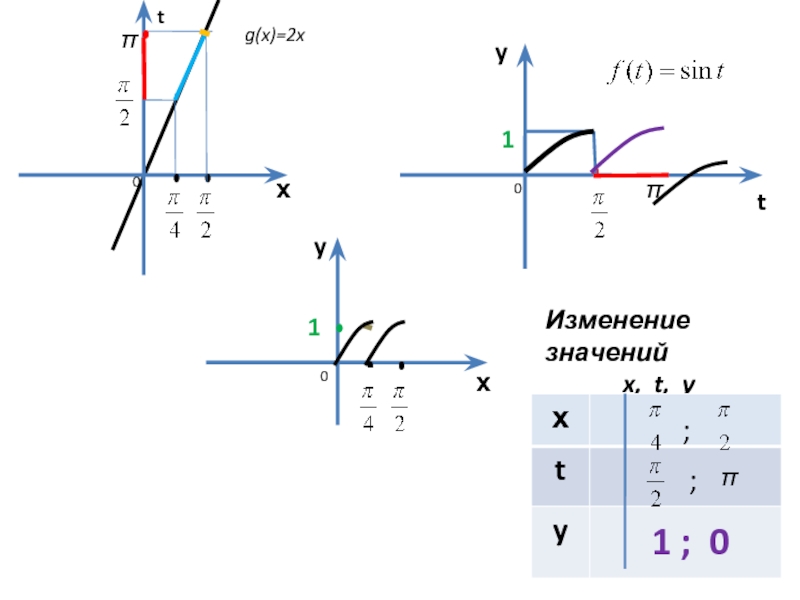
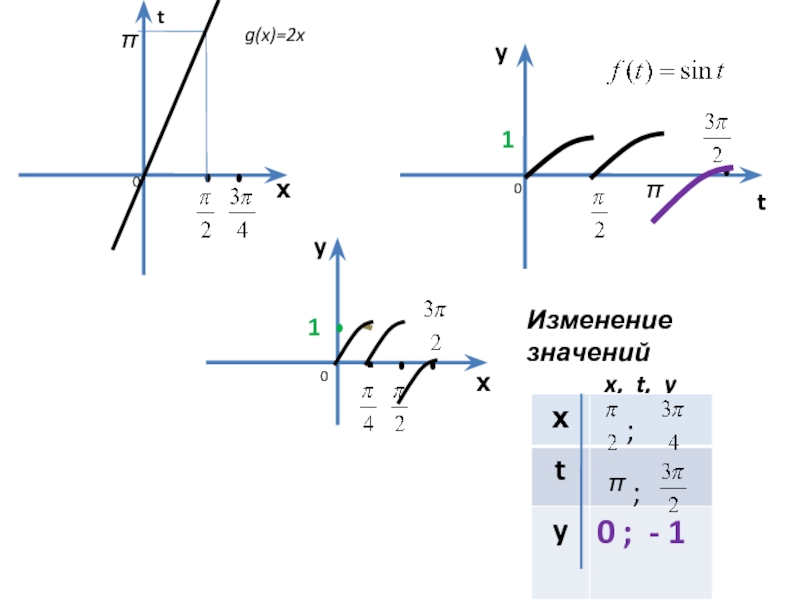
15. х t х y y t g(x)=2x
16. х t х y y g(x)=2x
17. х t х y y g(x)=2x
18. х t х y y g(x)=2x
19. Таблица изменений значений x, t, y
20. х t х y y g(x)=2x
21. Нахождение множества значений сложной функции Пример.
22. Множество значений сложной функции как

Содержание Введение понятия сложной функции Примеры построения графиков Множество значений сложной функции

Слайд 1СЛОЖНАЯ ФУНКЦИЯ

Сложная – не значит трудная!

Слайд 2Содержание
Введение понятия сложной функции

Примеры построения графиков

Множество значений сложной функции

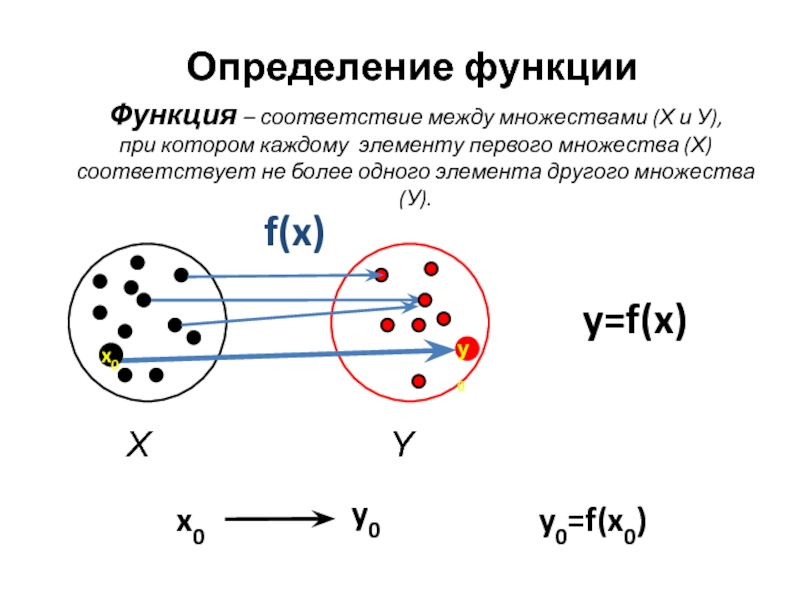
Слайд 3Определение функции

f(x)
y=f(x)
Y
X
y0=f(x0)
x0
y0
x0
у0
Функция – соответствие между множествами (Х и У), при котором каждому

элементу первого множества (Х) соответствует не более одного элемента другого множества (У).

Слайд 4Сложная функция Композиция двух функций
y=f(g(x))

g(x)
f(t)
T
Y
X
x0
t0
у0
x0

Слайд 5Формула для задания сложной функции

y=f(g(x)) –
– сложная функция

g(x) – внутренняя функция

f(t) – внешняя функция

Пример.

g(x) = х2 - 4 – внутренняя функция

f(t) = – внешняя функция

Слайд 6Примеры сложных функций
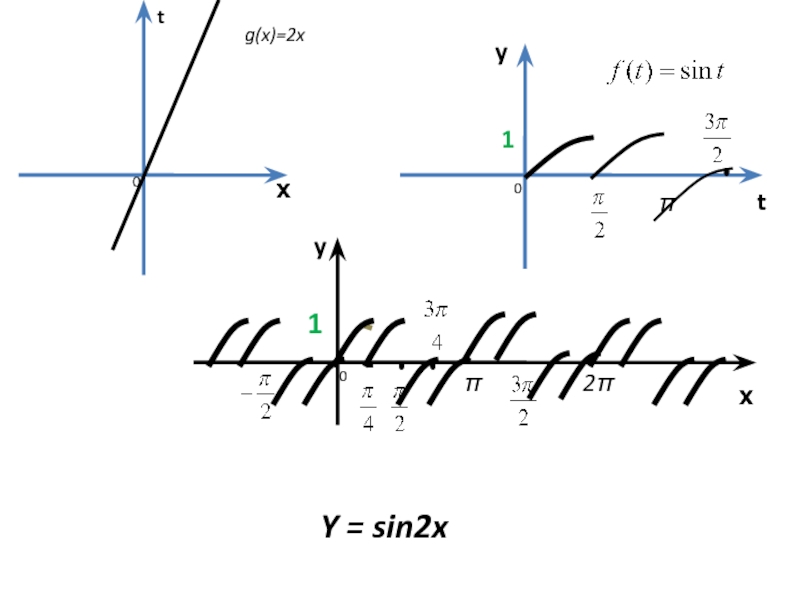
1. y = sin2x

2.

y = (x3 – 1 )5

3. y = cos(7x + 2)

4. y =

5. y = sin2x + 5sinx

Назовите
внутреннюю
и
внешнюю
функцию

Слайд 7Примеры построения графиков
Пример 1
Пример 2

y =

sin 2x

Слайд 8Пример 1
1. Найдем область определения функции:
D(y) =

(-∞; -2] U [2; +∞)
Функция четная.
Построим графики внутренней и внешней функции:

g(x)=x2-4

Слайд 9

х
t
х
y
y
t
2
g(x)=x2-4

x0
x0
t0
t0
y0
y0

-2
2
Как построить график
?
0
0
0

Слайд 10

х
t
х
y
y
t
2
g(x)=x2-4

-2
x0
t0
t0
y0
x0
2
-2
y0
Изменение значений
x, t, y

Слайд 11

0
Использование четности: график симметричен относительно оси ординат
х
y

-2
2
0

Слайд 12Пример 2
1. D(y) = R
Функция нечетная.

Функция периодическая, период: π.
Построим графики внутренней и внешней функции:

g(x)=2х

Слайд 13х
t
х
y
y
t
g(x)=2x

π

Как построить график y = sin2x ?
0
0
0

1

Слайд 14Таблица изменений значений x, t, y
x
t
y
π
0
;
;
;
;

Слайд 15х
t
х
y
y
t
g(x)=2x

π

1
0
0
0

1

Изменение значений
x, t, y

Слайд 16х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

;

1 ; 0

Слайд 17х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

;

Слайд 18х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

;

2π

;

2π

Слайд 19Таблица изменений значений x, t, y
x
t
y
π
0
;
;
;
;
0
;
0
1
;
;
;
π
1
0
π
0 ;

- 1

2π

- 1 ; 0

Слайд 20х
t
х
y
y
g(x)=2x

π
t

1
0
0

1

0
π
2π
Y = sin2x

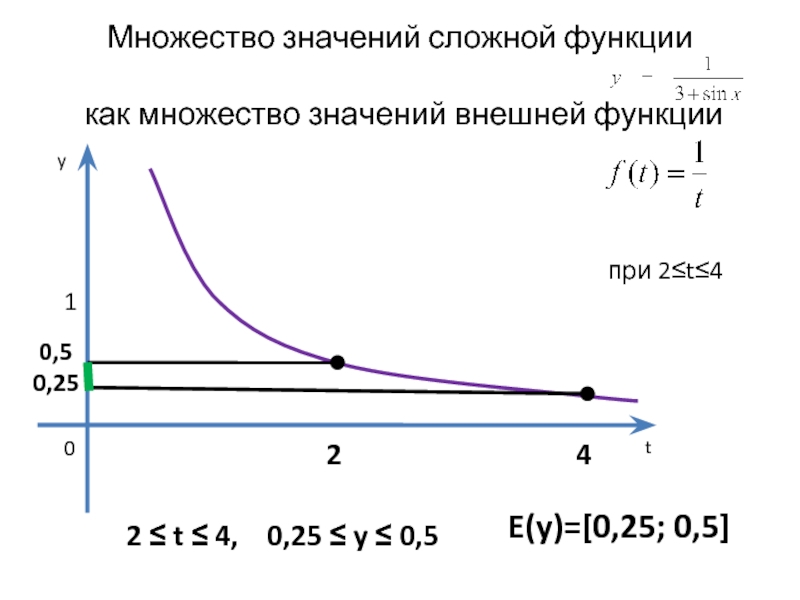
Слайд 21Нахождение множества значений сложной функции
Пример. Дана функция
Найдите Е(у).

Решение.
Внутренняя функция принимает значения от 2 до 4, так как 2≤3+sinx≤4.

Рассмотрим внешнюю функцию:

Заметим, что она определена только при тех значениях t, для которых
2≤t≤4.

Слайд 22Множество значений сложной функции как множество значений внешней функции

1
0,5
0,25
0
2
4
t
y
2 ≤ t

≤ 4, 0,25 ≤ y ≤ 0,5

E(y)=[0,25; 0,5]

при 2≤t≤4

Скачать презентацию

Сложная функция презентация

Содержание

Слайд 1СЛОЖНАЯ ФУНКЦИЯ

Сложная – не значит трудная!

Слайд 2Содержание
Введение понятия сложной функции

Примеры построения графиков

Множество значений сложной функции

Слайд 3Определение функции

f(x)
y=f(x)
Y
X
y0=f(x0)
x0
y0
x0
у0
Функция – соответствие между множествами (Х и У), при котором каждому

Слайд 4Сложная функция Композиция двух функций
y=f(g(x))

g(x)
f(t)
T
Y
X
x0
t0
у0
x0

Слайд 5Формула для задания сложной функции

Слайд 6Примеры сложных функций
1. y = sin2x

2.

Слайд 7Примеры построения графиков
Пример 1
Пример 2

y =

Слайд 8Пример 1
1. Найдем область определения функции:
D(y) =

Слайд 9

х
t
х
y
y
t
2
g(x)=x2-4

x0
x0
t0
t0
y0
y0

-2
2
Как построить график
?
0
0
0

Слайд 10

х
t
х
y
y
t
2
g(x)=x2-4

-2
x0
t0
t0
y0
x0
2
-2
y0
Изменение значений
x, t, y

Слайд 11

0
Использование четности: график симметричен относительно оси ординат
х
y

-2
2
0

Слайд 12Пример 2
1. D(y) = R
Функция нечетная.

Слайд 13х
t
х
y
y
t
g(x)=2x

π

Как построить график y = sin2x ?
0
0
0

1

Слайд 14Таблица изменений значений x, t, y
x
t
y
π
0
;
;
;
;

Слайд 15х
t
х
y
y
t
g(x)=2x

π

1
0
0
0

1

Изменение значений
x, t, y

Слайд 16х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

Слайд 17х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

Слайд 18х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

Слайд 19Таблица изменений значений x, t, y
x
t
y
π
0
;
;
;
;
0
;
0
1
;
;
;
π
1
0
π
0 ;

Слайд 20х
t
х
y
y
g(x)=2x

π
t

1
0
0

1

0
π
2π
Y = sin2x

Слайд 21Нахождение множества значений сложной функции
Пример. Дана функция
Найдите Е(у).

Слайд 22Множество значений сложной функции как множество значений внешней функции

1
0,5
0,25
0
2
4
t
y
2 ≤ t

Обратная связь

Что такое ThePresentation.ru?

Сложная функция презентация

Содержание

Слайд 1СЛОЖНАЯ ФУНКЦИЯСложная – не значит трудная!

Слайд 2СодержаниеВведение понятия сложной функцииПримеры построения графиковМножество значений сложной функции

Слайд 3Определение функцииf(x)y=f(x)YXy0=f(x0)x0y0x0у0Функция – соответствие между множествами (Х и У), при котором каждому

Слайд 4Сложная функция Композиция двух функцийy=f(g(x)) g(x)f(t)TYXx0t0у0x0

Слайд 5Формула для задания сложной функции

Слайд 6Примеры сложных функций 1. y = sin2x 2.

Слайд 7Примеры построения графиковПример 1Пример 2 y =

Слайд 8Пример 11. Найдем область определения функции: D(y) =

Слайд 9хtхyyt2g(x)=x2-4x0x0t0t0y0y0-22Как построить график ?000

Слайд 10хtхyyt2g(x)=x2-4-2x0t0t0y0x02-2y0Изменение значений x, t, y

Слайд 110Использование четности: график симметричен относительно оси ординатхy-220

Слайд 12Пример 21. D(y) = R Функция нечетная.

Слайд 13хtхyytg(x)=2xπКак построить график y = sin2x ?0001

Слайд 14Таблица изменений значений x, t, yxtyπ0;;;;

Слайд 15хtхyytg(x)=2xπ10001Изменение значений x, t, y

Слайд 16хtхyyg(x)=2xπt10001Изменение значений x, t, y

Слайд 17хtхyyg(x)=2xπt10001Изменение значений x, t, y

Слайд 18хtхyyg(x)=2xπt10001Изменение значений x, t, y

Слайд 19Таблица изменений значений x, t, y xtyπ0;;;;0;01;;;π10π0 ;

Слайд 20хtхyyg(x)=2xπt10010π2πY = sin2x

Слайд 21Нахождение множества значений сложной функцииПример. Дана функция Найдите Е(у).

Слайд 22Множество значений сложной функции как множество значений внешней функции10,50,25024ty2 ≤ t

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1СЛОЖНАЯ ФУНКЦИЯ

Сложная – не значит трудная!

Слайд 2Содержание
Введение понятия сложной функции

Примеры построения графиков

Множество значений сложной функции

Слайд 3Определение функции

f(x)
y=f(x)
Y
X
y0=f(x0)
x0
y0
x0
у0
Функция – соответствие между множествами (Х и У), при котором каждому

Слайд 4Сложная функция Композиция двух функций
y=f(g(x))

g(x)
f(t)
T
Y
X
x0
t0
у0
x0

Слайд 6Примеры сложных функций
1. y = sin2x

2.

Слайд 7Примеры построения графиков
Пример 1
Пример 2

y =

Слайд 8Пример 1
1. Найдем область определения функции:
D(y) =

Слайд 9

х
t
х
y
y
t
2
g(x)=x2-4

x0
x0
t0
t0
y0
y0

-2
2
Как построить график
?
0
0
0

Слайд 10

х
t
х
y
y
t
2
g(x)=x2-4

-2
x0
t0
t0
y0
x0
2
-2
y0
Изменение значений
x, t, y

Слайд 11

0
Использование четности: график симметричен относительно оси ординат
х
y

-2
2
0

Слайд 12Пример 2
1. D(y) = R
Функция нечетная.

Слайд 13х
t
х
y
y
t
g(x)=2x

π

Как построить график y = sin2x ?
0
0
0

1

Слайд 14Таблица изменений значений x, t, y
x
t
y
π
0
;
;
;
;

Слайд 15х
t
х
y
y
t
g(x)=2x

π

1
0
0
0

1

Изменение значений
x, t, y

Слайд 16х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

Слайд 17х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

Слайд 18х
t
х
y
y
g(x)=2x

π
t

1
0
0
0

1

Изменение значений
x, t, y

Слайд 19Таблица изменений значений x, t, y
x
t
y
π
0
;
;
;
;
0
;
0
1
;
;
;
π
1
0
π
0 ;

Слайд 20х
t
х
y
y
g(x)=2x

π
t

1
0
0

1

0
π
2π
Y = sin2x

Слайд 21Нахождение множества значений сложной функции
Пример. Дана функция
Найдите Е(у).

Слайд 22Множество значений сложной функции как множество значений внешней функции

1
0,5
0,25
0
2
4
t
y
2 ≤ t