Определение
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Скалярное произведение векторов презентация
Содержание
- 1. Скалярное произведение векторов
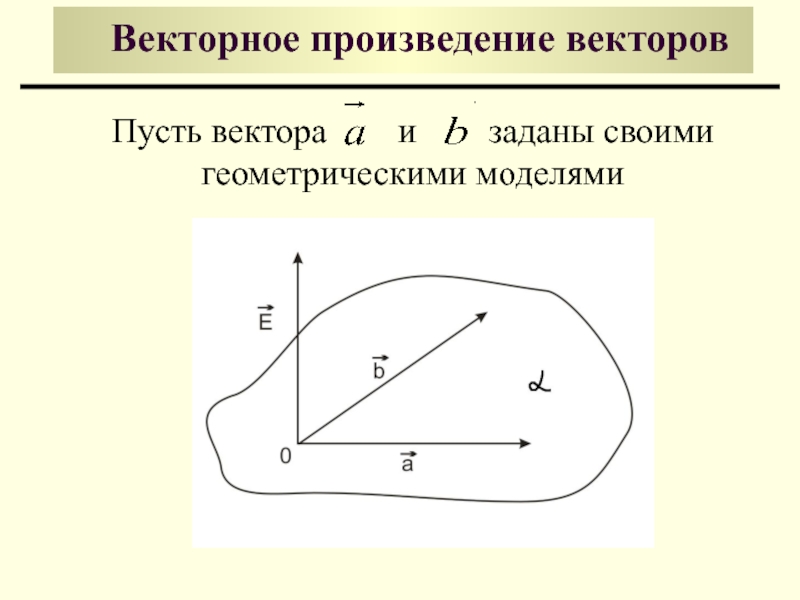
- 2. Векторное произведение векторов Пусть
- 3. Векторным произведением векторов и
- 4. Векторное произведение векторов
- 5. Векторное произведение векторов Соотношения между ортами
- 6. Векторное произведение векторов Пусть заданы два вектора Выражение векторного произведения через координаты
- 7. Векторное произведение векторов - площадь параллелограмма - площадь треугольника
- 8. Первые два вектора
- 9. Геометрический смысл смешанного произведения векторов
- 10. Смешанное произведение не меняется при
- 11. Если
Векторное произведение векторов Пусть вектора и заданы своими геометрическими моделями
Слайд 1
Скалярное произведение векторов
Скалярным произведением векторов называется
число, равное произведению длин этих векторов
на
косинус угла между ними
Слайд 3Векторным произведением векторов и
называется
новый вектор , который:
и плоскости векторов и
имеет длину, численно равную площади
параллелограмма, построенного на векторах
и как на сторонах , где
направлен так, что если смотреть с его
конца, то поворот от к по кратчайшему
углу виден против часовой стрелки
и плоскости векторов и
имеет длину, численно равную площади
параллелограмма, построенного на векторах
и как на сторонах , где
направлен так, что если смотреть с его
конца, то поворот от к по кратчайшему
углу виден против часовой стрелки
Векторное произведение векторов
Определение
Слайд 4
Векторное произведение векторов
Обозначение векторного произведения
или
Свойства векторного произведения
Слайд 6
Векторное произведение векторов
Пусть заданы два вектора
Выражение векторного произведения
через координаты
Слайд 8
Первые два вектора перемножаются векторно,
Рассмотрим
произведение векторов и
Смешанное произведение векторов
составленное следующим образом:
а их результат скалярно умножается на вектор
Такое произведение называется
смешанным произведением векторов
ОБОЗНАЧЕНИЕ
В результате смешанного произведения получается
число
Слайд 9
Геометрический смысл смешанного произведения векторов
Смешанное произведение трех векторов равно объему
параллелепипеда,
построенного на этих векторах
Слайд 10
Смешанное произведение не меняется при
циклической перестановке его сомножителей
Свойства смешанного произведения
векторов
Смешанное произведение не меняется при
перемене местами скалярного умножения
Слайд 11
Если
, то - компланарны
Свойства смешанного произведения векторов
Выражение смешанного произведения
через координаты
