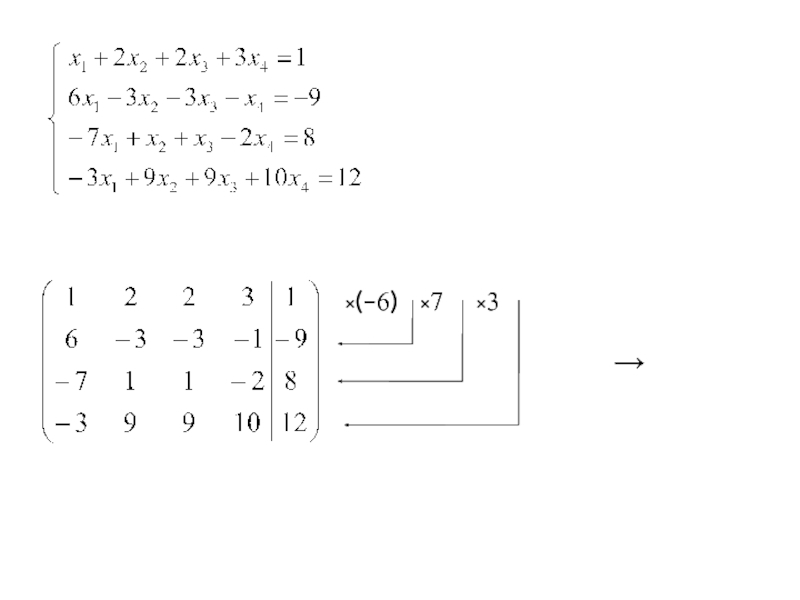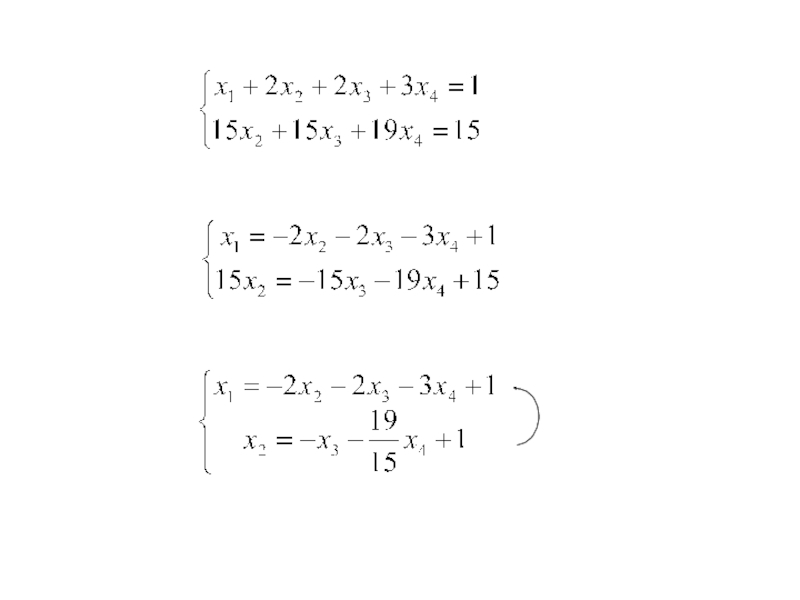- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы линейных уравнений. Метод Гаусса. (Тема 9.2) презентация
Содержание
- 1. Системы линейных уравнений. Метод Гаусса. (Тема 9.2)
- 2. Системой m линейных уравнений с n неизвестными
- 3. Решением системы (*) называется такой набор чисел
- 4. Система линейных уравнений
- 5. Если b1=b2=…=bm=0, то система называется однородной; в
- 6. Элементарными преобразованиями линейной системы называются следующие преобразования:
- 7. Систему (*) можно записать в матричной форме:
- 8. Расширенной матрицей системы (*) называется матрица
- 9. Исследование системы линейных уравнений. Теорема Кронекера-Капелли.
- 10. Исследовать систему линейных уравнений означает определить, совместна
- 11. Правила решения произвольной системы линейных уравнений.
- 12. Выразить базисные (главные) неизвестные через свободные.
- 13. 3. Метод Гаусса Систему уравнений приводят к
- 14. 1. Исследовать систему линейных уравнений. Если
- 15. Прямой ход ×(-2) ×(-1) ×(-3) →
- 16. → : (-4) + ×3 → ×2
- 17. обратный ход Ответ: (1; 2; 3; 4)
- 18. 2. Исследовать систему линейных уравнений. Если
- 19. ×(-6) ×7 ×3 →
- 20. → + → rang(A)=rang(A|B)=2
- 22. общее решение х1 х2
- 23. пусть тогда частное решение Ответ:
- 24. 3. Исследовать систему линейных уравнений. Если
- 25. → rang(A)≠rang(A|B) ⇒ система несовместна rang(A)=2; rang(A|B)=3 А A|B Ответ: система несовместна
- 26. Если b1=b2=…=bm=0, то система называется однородной.
- 27. Однородная система линейных уравнений. Пусть
- 28. Однородная система всегда совместна, так как существует
- 29. 1. Решить систему линейных уравнений :
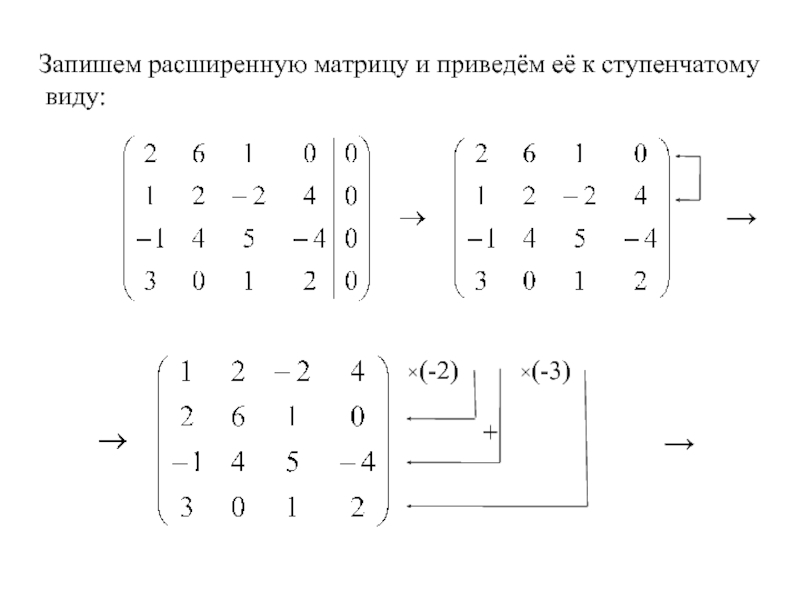
- 30. Запишем расширенную матрицу и приведём её к
- 31. ×(-3) ×3 → : 2 : 12 ×11
- 32. rang(A)=rang(A|B)=4=(n=4) ⇒ система совместна
- 33. Ответ: (0, 0, 0, 0)
- 34. 2. Решить систему линейных уравнений :
- 35. rang(A)=rang(A|B)=2
- 36. ⇒ Тогда общее решение системы: (0, х3, х3)
- 37. Пусть , тогда частное решение:
Системой m линейных уравнений с n неизвестными х1, х2, …, хn называется система вида aij - коэффициенты системы, i=1,…,m; j=1,…,n bi - свободные члены.
Слайд 2Системой m линейных уравнений с n неизвестными х1, х2, …, хn
называется система вида
aij - коэффициенты системы, i=1,…,m; j=1,…,n
bi - свободные члены.
aij - коэффициенты системы, i=1,…,m; j=1,…,n
bi - свободные члены.
(*)
Слайд 3Решением системы (*) называется такой набор чисел (с1, с2,…, сn), что
при его подстановке в систему вместо соответствующих неизвестных (с1 вместо х1, …, сn вместо хn) каждое из уравнений системы обращается в тождество.
Слайд 4
Система линейных уравнений
Совместная
(имеет хотя бы одно решение)
Несовместная
(не имеет ни одного решения)
Определённая
(имеет
единственное решение)
Неопределённая
(имеет более одного решения-
бесконечное множество решений)
В случае неопределённой системы каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Слайд 5Если b1=b2=…=bm=0, то система называется однородной; в противном случае она называется
неоднородной.
Две системы называются эквивалентными или равносильными, если любое решение одной из них является также решением другой, т.е. если они имеют одно и то же множество решений.
(любые две несовместные системы считаются эквивалентными)
Слайд 6Элементарными преобразованиями линейной системы называются следующие преобразования:
- перестановка уравнений системы;
- умножение
или деление коэффициентов и свободных членов на одно и то же число, отличное от нуля;
- сложение и вычитание уравнений;
- исключение из системы тех уравнений, в которых все коэффициенты и свободные члены равны нулю.
- сложение и вычитание уравнений;
- исключение из системы тех уравнений, в которых все коэффициенты и свободные члены равны нулю.
Слайд 7Систему (*) можно записать в матричной форме: АХ=В,
где
матрица коэффициентов системы;
матрица-столбец
(вектор-столбец)
неизвестных
матрица-столбец
(вектор-столбец)
свободных членов
Слайд 9Исследование системы линейных уравнений.
Теорема Кронекера-Капелли.
Система линейных уравнений (*) совместна тогда
и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы:
Слайд 10Исследовать систему линейных уравнений означает определить, совместна она или нет, а
для совместной системы- выяснить, является ли она определенной или нет.
Если rang(A)≠rang(A|B), то система несовместна.
2) Если rang(A)=rang(A|B)=n (где n- число неизвестных), то система совместна и определённа (имеет единственное решение).
3) Если rang(A)=rang(A|B)
Слайд 11Правила решения произвольной системы линейных уравнений.
Найти ранги основной и расширенной
матриц системы. Если rang(A)≠rang(A|B), то система несовместна.
Если rang(A)=rang(A|B)=r, то система совместна. Найти какой-либо базисный минор порядка r. Взять r уравнений, из элементов которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор, называют базисными или главными, а остальные n-r неизвестных называют свободными.
Если rang(A)=rang(A|B)=r, то система совместна. Найти какой-либо базисный минор порядка r. Взять r уравнений, из элементов которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор, называют базисными или главными, а остальные n-r неизвестных называют свободными.
Слайд 12Выразить базисные (главные) неизвестные через свободные.
Придавая свободным неизвестным произвольные
значения, получим соответствующие значения базисных (главных) неизвестных. Таким образом находим частные решения исходной системы уравнений.
Слайд 133. Метод Гаусса
Систему уравнений приводят к эквивалентной ей системе с треугольной
матрицей (к ступенчатому виду).
Из полученной треугольной системы переменные находят с помощью последовательных подстановок.
Из полученной треугольной системы переменные находят с помощью последовательных подстановок.
(метод последовательного исключения неизвестных)
Слайд 14
1. Исследовать систему линейных уравнений. Если она совместна, то найти её
общее и одно частное решение.
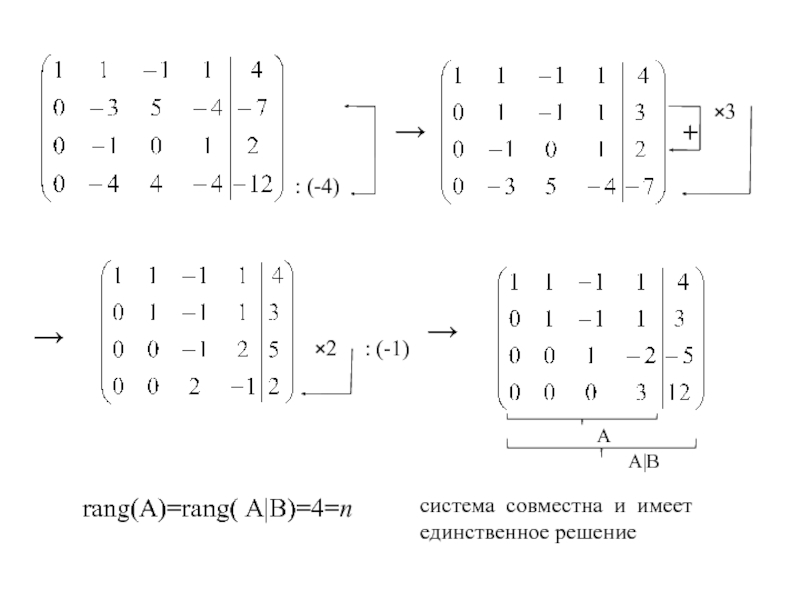
Слайд 16→
: (-4)
+
×3
→
×2
: (-1)
→
rang(A)=rang( A|B)=4=n
система совместна и имеет единственное решение
А
A|B
Слайд 18
2. Исследовать систему линейных уравнений. Если она совместна, то найти её
общее и одно частное решение.
Слайд 23
пусть
тогда частное решение
Ответ:
общее решение:
частное решение:
Делаем проверку и записываем ответ:
Слайд 24
3. Исследовать систему линейных уравнений. Если она совместна, то найти её
общее и одно частное решение.
×(-1)
×2
→
×(-2)
→
Слайд 25→
rang(A)≠rang(A|B) ⇒ система несовместна
rang(A)=2; rang(A|B)=3
А
A|B
Ответ: система несовместна
Слайд 27 Однородная система линейных уравнений.
Пусть дана система m линейных однородных уравнений
с n неизвестными х1, х2, …, хn:
Слайд 28Однородная система всегда совместна, так как существует тривиальное решение х1= х2=…=хn=0
Однородная
система имеет бесконечное множество решений, тогда и только тогда, когда rang(A)
Слайд 32
rang(A)=rang(A|B)=4=(n=4) ⇒
система совместна и определённа, то есть имеет единственное
решение х1= х2= х3 =х4=0.
А
A|B
Слайд 37
Пусть
, тогда частное решение:
Ответ:
общее решение: (0; х3; х3)
частное решение: (0; 1; 1)
(0;
1; 1)
Делаем проверку и получаем ответ:
