- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
shag v budushchee презентация
Содержание
- 1. shag v budushchee
- 2. «Мышление- это не
- 3. С точки зрения психологии: В психологии мышление —
- 4. ВИДЫ МЫШЛЕНИЯ: Наглядно-действенное Наглядно-образное Словесно понятийное
- 5. МАТЕМАТИЧЕСКОЕ МЫШЛЕНИЕ. Математическое мышление является
- 6. Основные компоненты математического мышления Конкретное Неоперативное
- 7. Функциональное мышление Абстрактное аналитическое мышление логическое мышление пространственное мышление
- 8. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.
- 9. В программе ставится цель не
- 10. Эта система включает: а)задачи
- 11. СПЕЦИФИКА КОМБИНАТОРНЫХ РАССУЖДЕНИЙ ПОЗВОЛЯЕТ РЕАЛИЗОВАТЬ СЛЕДУЮЩИЕ ЦЕЛИ
- 12. ВЫДЕЛЯЮТСЯ ТРИ ОСНОВНЫХ ВИДА КОМБИНАТОРНЫХ ЗАДАЧ.
- 13. В системе комбинаторных задач выделено два блока
- 14. План работы факультатива Цель: формирование мыслительных операций в процессе решения комбинаторных задач
- 15. План работы факультатива
- 16. КОМБИНАТО́РИКА (Комбинаторный анализ) Комбинато́рика
- 17. Комбинаторика- раздел математики, изучающий дискретные
- 18. ДЕРЕВО ВОЗМОЖНЫХ ВАРИАНТОВ
- 19. ЗАДАЧА 1 В класс пришли четыре новых
- 20. ЗАДАЧА 1 12 вариантов
- 21. ОРГАНИЗОВАННЫЙ ПЕРЕБОР
- 22. ЗАДАЧА 3 На цветочной клумбе сидели шмель,
- 23. ЗАДАЧА 3
- 24. ЗАДАЧА 16 У Кати 2 кофты и
- 25. ЗАДАЧА 16 Не может
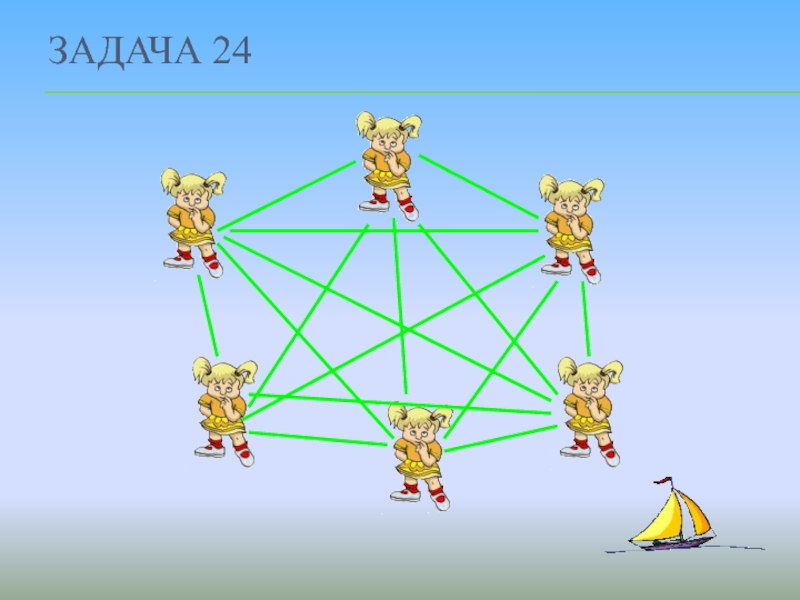
- 26. ЗАДАЧА 24 Шесть девочек взяли напрокат двухместную
- 27. ЗАДАЧА 24
- 29. СПИСОК ЛИТЕРАТУРЫ: Математика. 1-4кл. Программа для общеобразоват.
Слайд 1ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОГО МЫШЛЕНИЯ ПРИ ПРОПЕДЕВТИКЕ «ЭЛЕМЕНТОВ КОМБИНАТОРИКИ В НАЧАЛЬНОЙ ШКОЛЕ.»
Выполнил: учитель
Усачёва Наталия Андреевна
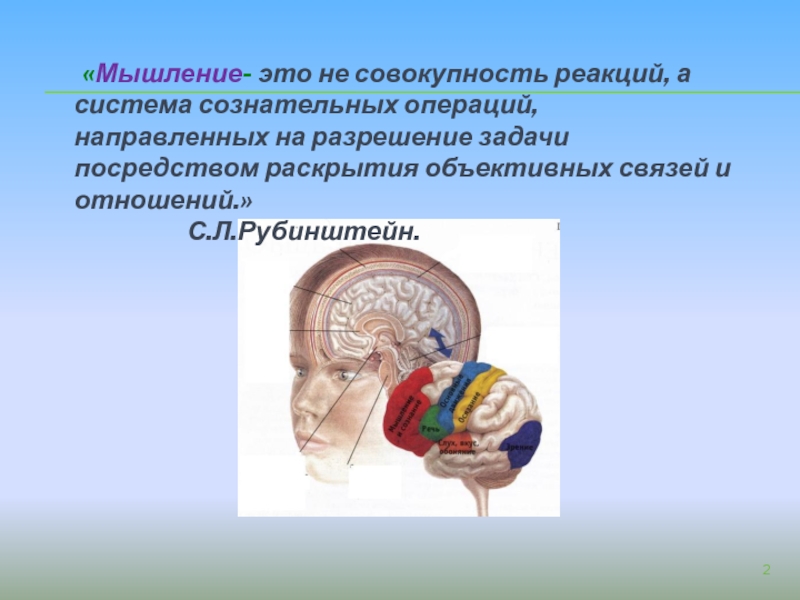
Слайд 2 «Мышление- это не совокупность реакций, а система
С.Л.Рубинштейн.
Слайд 3С точки зрения психологии:
В психологии мышление — совокупность умственных процессов, лежащих в
Мышление — опосредованное и обобщённое отражение действительности, вид умственной деятельности, заключающейся в познании сущности вещей и явлений, закономерных связей и отношений между ними.
Мышление как одна из психических функций — психический процесс отражения и познания существенных связей и отношений предметов и явлений объективного мира.
Мышление - это высший познавательный процесс. - это движение идей, раскрывающее суть вещей. Его итогом является не образ, а некоторая мысль, идея.
Слайд 5МАТЕМАТИЧЕСКОЕ МЫШЛЕНИЕ.
Математическое мышление является не только одним из важнейших компонентов
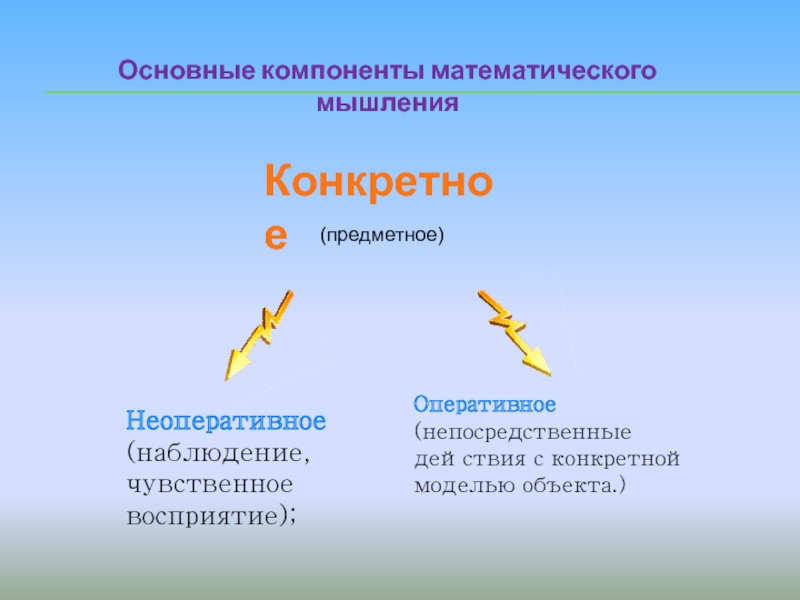
Слайд 6Основные компоненты математического мышления
Конкретное
Неоперативное
(наблюдение, чувственное восприятие);
Оперативное
(непосредственные действия с конкретной моделью
(предметное)
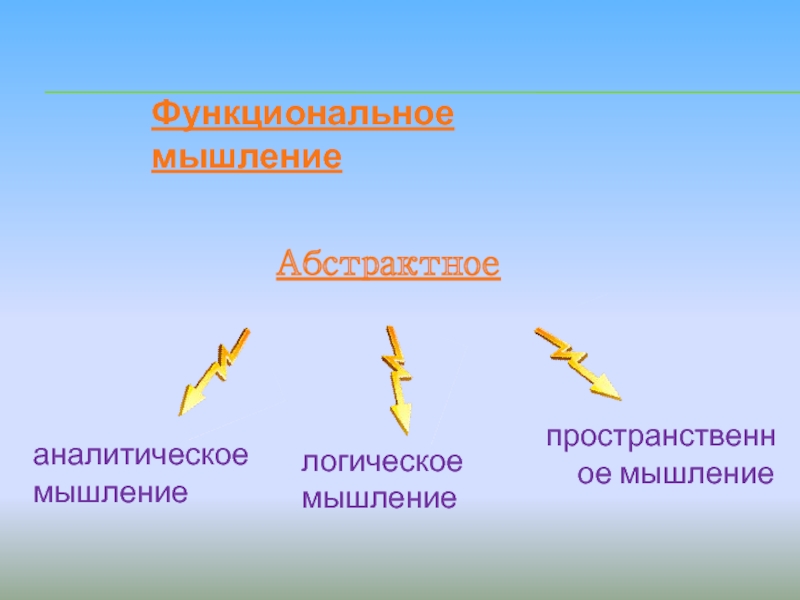
Слайд 7Функциональное мышление
Абстрактное
аналитическое мышление
логическое мышление
пространственное мышление
Слайд 9 В программе ставится цель не только обучить перебору, но
Слайд 10 Эта система включает:
а)задачи на выяснение возможности существования комбинаторного
б) обратные комбинаторные задачи;
в) задачи с разными способами упорядочения (слева направо, сверху вниз, по кругу и т.д.);
г) задачи с ограничениями на составляемые комбинаторные соединения.
Слайд 11СПЕЦИФИКА КОМБИНАТОРНЫХ РАССУЖДЕНИЙ ПОЗВОЛЯЕТ РЕАЛИЗОВАТЬ СЛЕДУЮЩИЕ ЦЕЛИ И ЗАДАЧИ ОБУЧЕНИЯ МАТЕМАТИКЕ:
Развитие
Совершенствование умственных операций (анализа, синтеза, сравнения, планирования, обобщения и абстрагирования).
Развитие образного, словесно- логического и наглядно- действенного компонентов мышления в их взаимосвязи.
Слайд 12ВЫДЕЛЯЮТСЯ ТРИ ОСНОВНЫХ ВИДА КОМБИНАТОРНЫХ ЗАДАЧ.
1. Задачи на нахождение
2. Задачи на нахождение размещений, т.е. задачи на выбор подмножеств с учетом порядка их элементов.
3. Задачи на нахождение сочетаний, т.е. задачи на выбор подмножеств без учета порядка их элементов.
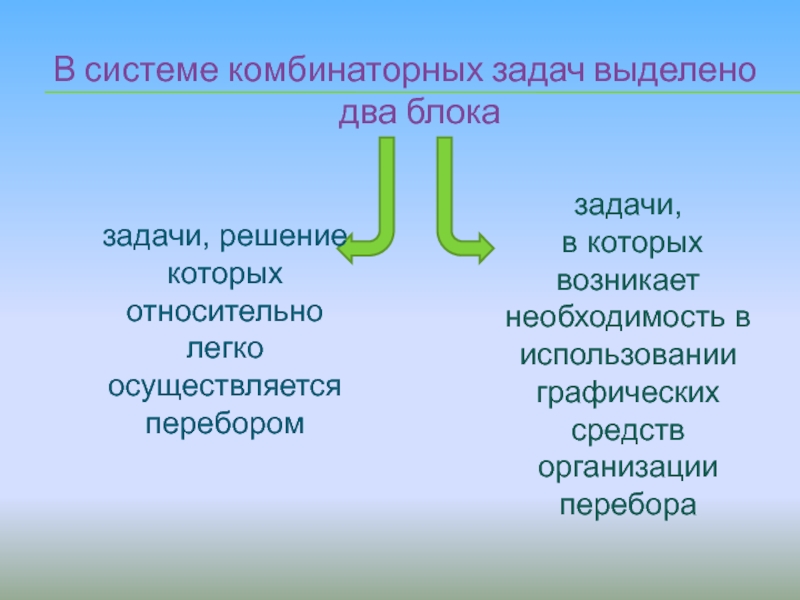
Слайд 13В системе комбинаторных задач выделено два блока
задачи, решение которых относительно легко
задачи,
в которых возникает необходимость в использовании графических средств организации перебора
Слайд 14План работы факультатива
Цель: формирование мыслительных операций в процессе решения комбинаторных задач
Слайд 17 Комбинаторика- раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки,
размещения и перечисления элементов) и
на них.
Слайд 19ЗАДАЧА 1
В класс пришли четыре новых ученика Миша, Вася, Катя, Лиза.
Решение
Задачи, решаемые
с помощью дерева
возможных вариантов
Слайд 22ЗАДАЧА 3
На цветочной клумбе сидели шмель, жук, стрекоза, бабочка и муха.
Решение
Задачи, решаемые
методом
организованного перебора
Слайд 24ЗАДАЧА 16
У Кати 2 кофты и 3 юбки – все разного
Решение
Слайд 26ЗАДАЧА 24
Шесть девочек взяли напрокат двухместную лодку. Построй граф, на котором
Решение
Слайд 29СПИСОК ЛИТЕРАТУРЫ:
Математика. 1-4кл. Программа для общеобразоват. Учреждений/О.А.Ивашова и др. – 2-е
Фридман Л.М. Психолого – педагогические основы обучения математике в школе: Учителю математике о пед. Психологии.- М.:Просвещение, 1983.-160с., ил.
Гусев В.А. Психолого-педагогические основы обучения математике.-М.: ООО «Издательство «Вербум-М»,ООО «Издательский центр «Академия», 2003.-432с.