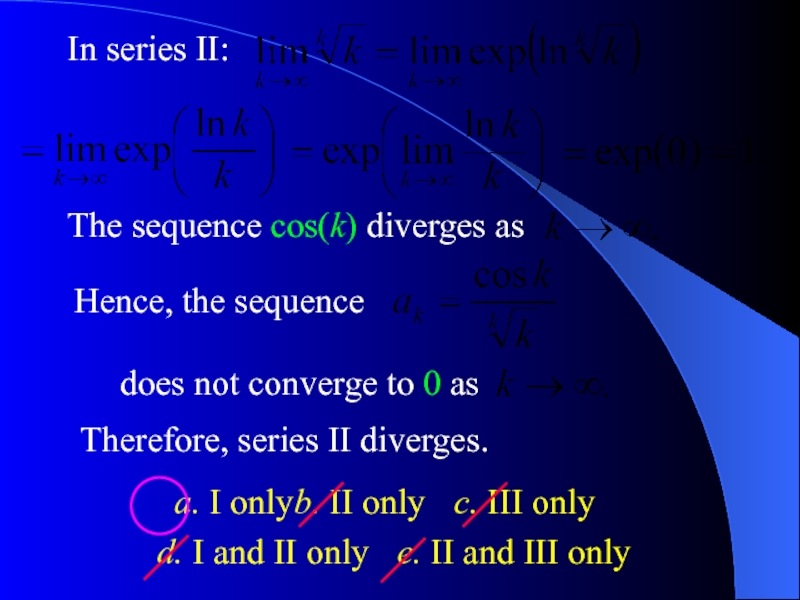- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
The Taylor Formula презентация
Содержание
- 1. The Taylor Formula
- 2. The Taylor Formula where For instance, where
- 3. Question 1. If Solution: Taylor’s formula tells
- 4. Therefore
- 5. Answers to Questions from Light #7:
- 6. Calculus++ Infinite Series
- 7. Question 1. What is the greatest value
- 8. Using the properties (ii) and (iii) we
- 9. In particular, where That is
- 10. Question 2. Use the Taylor formula to
- 11. an integer number Contradiction! Thus, our
- 12. Question 3. Find Solution. The Taylor formula
- 13. Since sin x is equivalent to x,
- 14. Consider an infinite sequence If we add
- 15. The sum of the first n terms
- 16. If |b| < 1, the sequence Sn
- 17. If b = 1, the sequence of
- 18. A necessary condition for convergence. If a
- 19. Question 5. Which of the following series
- 20. a. I only b. II only c. III only
- 21. Important series. This series converges if q > 1, and it diverges if
- 22. Question 5. A certain ball has the
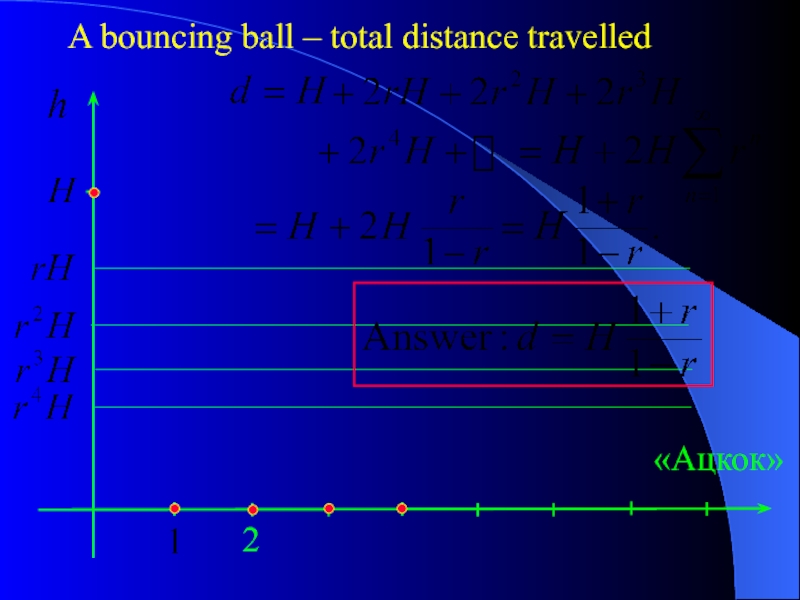
- 23. «Ацкок» 2 A bouncing ball – total distance travelled
- 24. Question 7. A certain ball has the
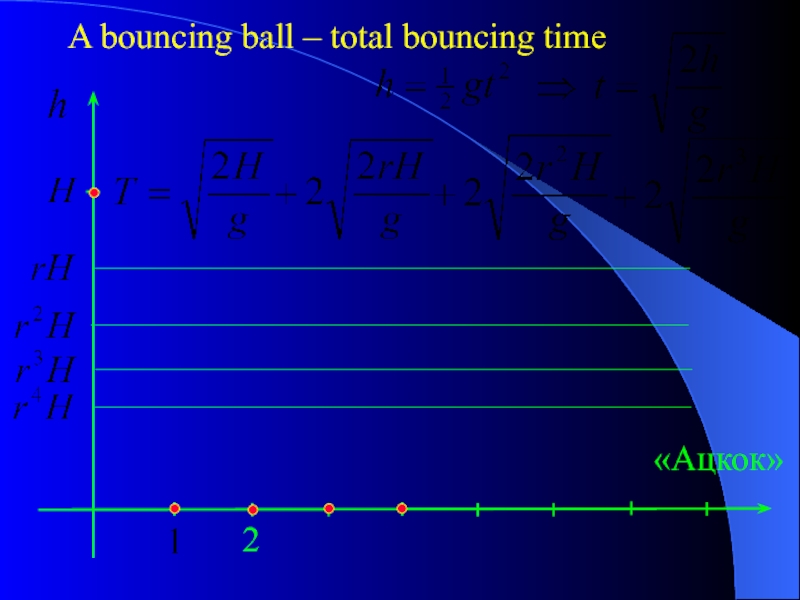
- 25. «Ацкок» 2 A bouncing ball – total bouncing time
- 27. Question 7. c) Suppose that each time
- 28. Hence, the ball that rebounds with velocity
Слайд 5 Answers to Questions from Light #7:
Taylor’s Formula & Infinite Series
Question
Question 4:
Question 3:
Слайд 7Question 1. What is the greatest value of b for which
(i) f (x) is infinitely differentiable for all x;
(ii) f (0) = 1, and
(iii) for all
Solution: Taylor’s formula tells us
Слайд 8Using the properties (ii) and (iii) we obtain
Solve the equation to
Therefore, the greatest value of b for which f (1) < 5 is 12.
Слайд 10Question 2. Use the Taylor formula to show that e is
Solution. Let us assume that e is rational,
Then the Taylor formula tells us that for any n:
Take
and multiply both sides
of the double inequality by n! to obtain
Слайд 11an integer number
Contradiction!
Thus, our assumption that e is a rational number
Therefore, e is an irrational number.
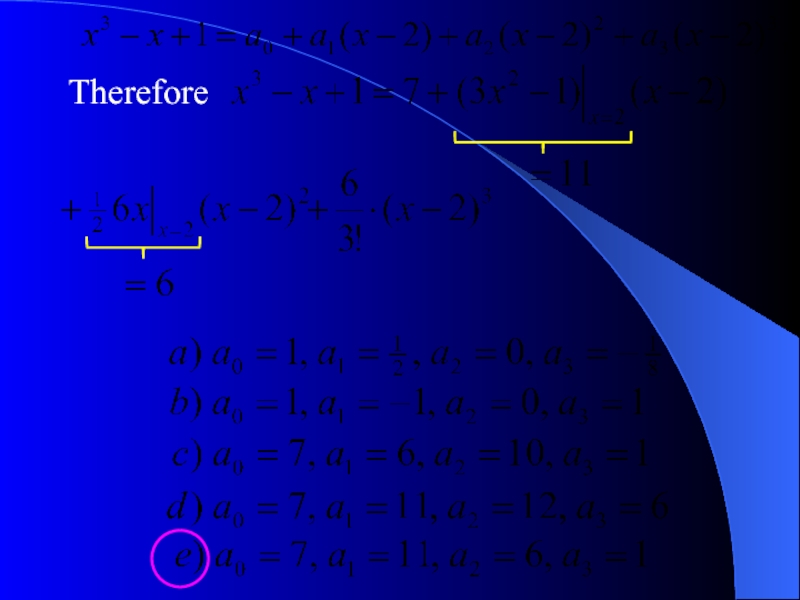
Therefore
Слайд 12Question 3. Find
Solution. The Taylor formula tells us that for any
Therefore
where is a number between 0 and 1.
Multiply by to obtain
= M, an integer number
Слайд 14Consider an infinite sequence
If we add all the terms of this
For example, consider the sequence
The corresponding infinite series is
What is the value of this infinite series?
This infinite series does not have a value.
or ?!
Слайд 15The sum of the first n terms of an infinite series,
An infinite series converges, if converges the sequence of its partial sums:
The limit, S, of the sequence of partial sums is the sum of the infinite series.
Слайд 16If |b| < 1, the sequence Sn converges.
Example. The geometric series
The n-th partial sum of the geometric series is given by
If and |b| > 1, the sequence of partial sums Sn diverges.
If a = 0, the sequence Sn converges to 0.
Слайд 17If b = 1, the sequence of partial sums Sn diverges
If b = –1, the sequence of partial sums Sn also diverges (again, unless a = 0).
Слайд 18A necessary condition for convergence.
If a series
converges, then
Indeed, if the sequence
converges, then (Cauchy criterion)
and
Set m = 1, then
Therefore
Слайд 19Question 5. Which of the following series converge?
a. I only b.
d. I and II only e. II and III only
Solution: For series III:
Hence, series III diverges.
Слайд 20a. I only b. II only c. III only
d. I and II only e.
The sequence cos(k) diverges as
Hence, the sequence
does not converge to 0 as
Therefore, series II diverges.
In series II:
Слайд 22Question 5. A certain ball has the property that each time
Suppose that the ball is dropped from an initial height of H meters.
a) Assuming that the ball continues to bounce indefinitely, find the total distance that it travels.
Solution:
Слайд 24Question 7. A certain ball has the property that each time
Suppose that the ball is dropped from an initial height of H meters.
b) Calculate the total time that the ball spends bouncing.
Hint: A ball having zero velocity falls ½ gt2 meters in t seconds.
Solution: Actually, philosophers might find it obvious that the ball never stop bouncing.
Слайд 27Question 7. c) Suppose that each time the ball strikes the
How long will it take for the ball to come to rest?
Solution:
The velocity of the ball when it hits the ground for the first time is given by
where
Слайд 28Hence, the ball that rebounds with velocity v1 will reach the
In our case
Hence
Therefore
and