- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сабақтың тақырыбы: Дискреттік математика негіздері. Лекция 2 презентация
Содержание
- 1. Сабақтың тақырыбы: Дискреттік математика негіздері. Лекция 2
- 2. Жоспары: Жиындар теориясы Жиындар және олармен орындалатын
- 3. Жиын. Негізгі түсініктер Жиын деп анықталған
- 4. Жиындармен орындалатын амалдар Біріктіру A∪B = {x |x∈A
- 5. Біріктіру А және В жиындарын біріктіру деп
- 6. Қиылысу А және В жиындарының қиылысуы деп,
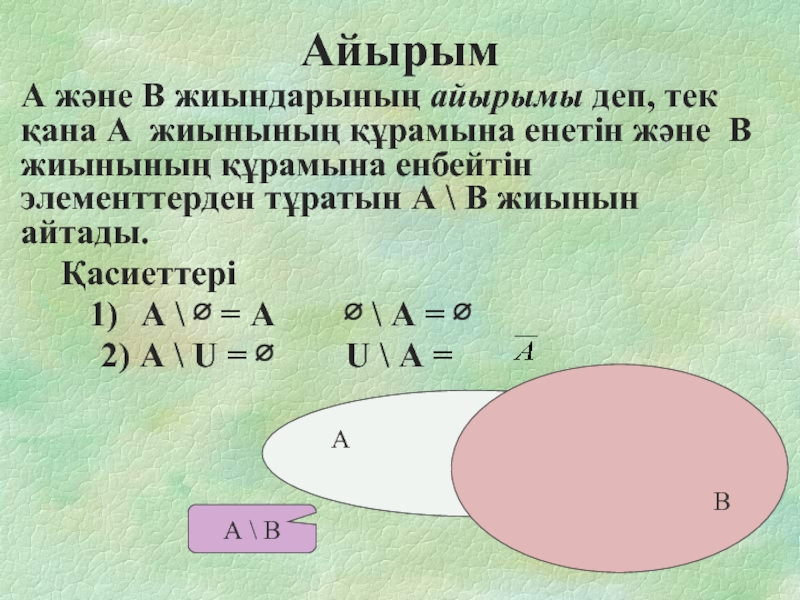
- 7. Айырым А және В жиындарының айырымы деп,
- 8. Симметриялық айырым А және В жиындарының
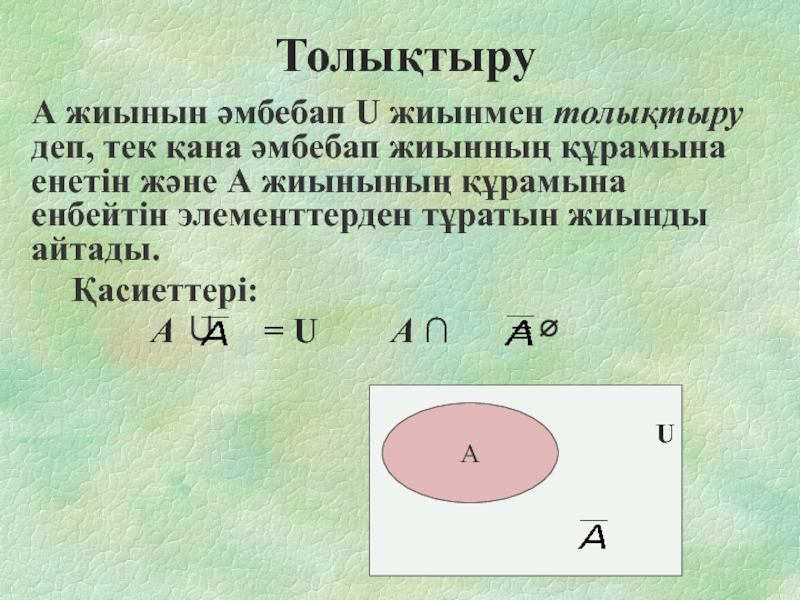
- 9. Толықтыру А жиынын әмбебап U жиынмен
- 10. Функциялар Функция дегеніміз – бір айнымалының өзгеруіне
- 11. Қатынас Қатынас деп әр түрлі нысандар
- 12. Қатынастар
- 13. Қатынастар қасиеттері Рефлексивтік х R х
- 14. Граф деп өзара байланысқан нысандар жиынтығын
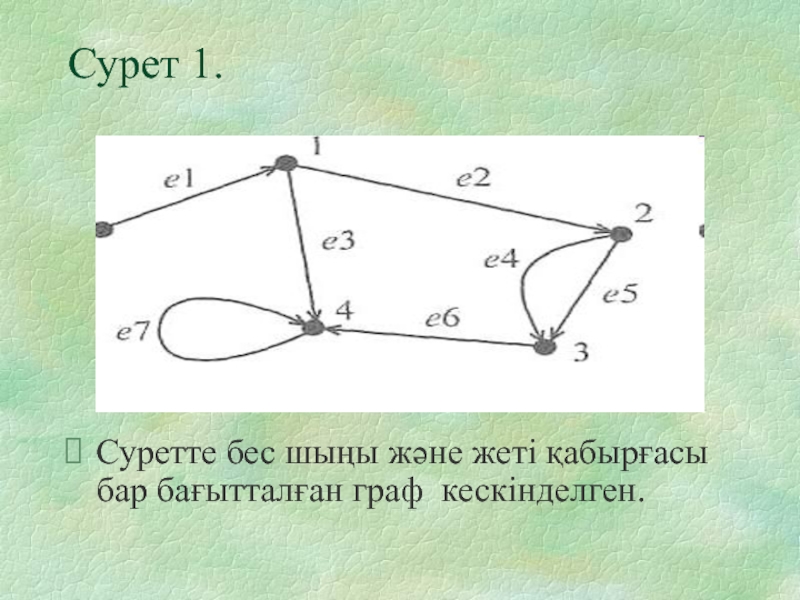
- 15. Сурет 1. Суретте бес шыңы және жеті қабырғасы бар бағытталған граф кескінделген.
- 16. Графтың түрлері Егер графтың барлық қабырғалары бағытталмаған
- 17. Егер екі шың екі немесе одан
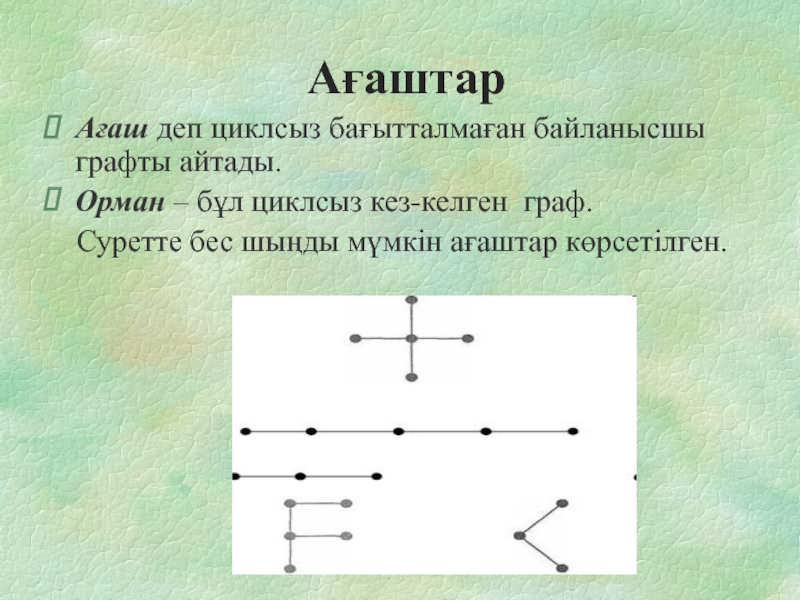
- 18. Ағаштар Ағаш деп циклсыз бағытталмаған байланысшы
- 19. Бақылау сұрақтары: Жиын анықтамасын
Слайд 2Жоспары:
Жиындар теориясы
Жиындар және олармен орындалатын амалдар
Функциялар
Қатынастар
Графтар теориясы
Негізгі түсініктері.
Графтың түрлері.
Ағаштар.
Слайд 3Жиын. Негізгі түсініктер
Жиын деп анықталған нысандардың бірге топтасуын айтады.
Жиынның
элементі деп жиынның жекеше
нысанын айтады.
Бос жиын ∅ деп, құрамында бір де бір элемент жоқ жиынды айтады.
Әмбебап жиын (универсум) U деп, қарастырылған барлық қолданылатын элементтер жиынын айтады
нысанын айтады.
Бос жиын ∅ деп, құрамында бір де бір элемент жоқ жиынды айтады.
Әмбебап жиын (универсум) U деп, қарастырылған барлық қолданылатын элементтер жиынын айтады
Слайд 4Жиындармен орындалатын амалдар
Біріктіру A∪B = {x |x∈A ∨ x∈B}
Қиылысу A∩B = {x |x∈A
& x∈B}
Айырым A\B = {x |x∈A & x∉B}
Симметриялық айырым
A/B = (A∪B)\(A∩B ) = {x | (x∈A & x∉B) ∨ (x∉A & x∈B)}
Толықтыру = {x | x ∉ A} = U\A, мұндағы U - әмбебап жиын.
Айырым A\B = {x |x∈A & x∉B}
Симметриялық айырым
A/B = (A∪B)\(A∩B ) = {x | (x∈A & x∉B) ∨ (x∉A & x∈B)}
Толықтыру = {x | x ∉ A} = U\A, мұндағы U - әмбебап жиын.
Слайд 5Біріктіру
А және В жиындарын біріктіру деп А немесе В жиындарының ең
болмағанда бірінің құрамына енетін элементтерден тұратын
А ∪ В жиынын айтады.
Қасиеттері
1) рефлексивтік А ∪ А = A
2) коммутативтік А ∪ В = В ∪ А
3) ассоциативтік
А ∪ (В∪С) = (А∪В) ∪ С = А ∪ В ∪ С
4) Бос жиынмен біріктіру А ∪ ∅ = А
5) Әмбебап жиынмен біріктіру А ∪ U = U
А ∪ В жиынын айтады.
Қасиеттері
1) рефлексивтік А ∪ А = A
2) коммутативтік А ∪ В = В ∪ А
3) ассоциативтік
А ∪ (В∪С) = (А∪В) ∪ С = А ∪ В ∪ С
4) Бос жиынмен біріктіру А ∪ ∅ = А
5) Әмбебап жиынмен біріктіру А ∪ U = U
Слайд 6Қиылысу
А және В жиындарының қиылысуы деп, А немесе В жиындарының құрамына
бірдей енетін элементтерден тұратын А ∩ В жиынын айтады.
Қасиеттері:
1) рефлексивтік А ∩ А = A
2) коммутативтік А ∩ В = В ∩ А
3) ассоциативтік
А ∩ (В∩С) = (А∩В) ∩ С = А ∩ В ∩ С
4) Бос жиынмен қиылысу А ∩ ∅ = ∅
5) Әмбебап жиынмен қиылысу А ∩ U = А
Қасиеттері:
1) рефлексивтік А ∩ А = A
2) коммутативтік А ∩ В = В ∩ А
3) ассоциативтік
А ∩ (В∩С) = (А∩В) ∩ С = А ∩ В ∩ С
4) Бос жиынмен қиылысу А ∩ ∅ = ∅
5) Әмбебап жиынмен қиылысу А ∩ U = А
Слайд 7Айырым
А және В жиындарының айырымы деп, тек қана А жиынының құрамына
енетін және В жиынының құрамына енбейтін элементтерден тұратын А \ В жиынын айтады.
Қасиеттері
А \ ∅ = А ∅ \ А = ∅
2) А \ U = ∅ U \ А =
Қасиеттері
А \ ∅ = А ∅ \ А = ∅
2) А \ U = ∅ U \ А =
Слайд 8Симметриялық айырым
А және В жиындарының симметриялық айырымы деп тек қана
А және В жиындарының бірігуінде жататын және олардың қиылысуында жатпайтын элементтерден тұратын жиынды айтады.
Қасиеттері:
1) Коммутативтік А / В = В / А
2) Ассоциативтік А/(В/С) = (А/В)/С =А/В/С
3) А / ∅ = А
4) А / U =
Қасиеттері:
1) Коммутативтік А / В = В / А
2) Ассоциативтік А/(В/С) = (А/В)/С =А/В/С
3) А / ∅ = А
4) А / U =
Слайд 9 Толықтыру
А жиынын әмбебап U жиынмен толықтыру деп, тек қана әмбебап
жиынның құрамына енетін және А жиынының құрамына енбейтін элементтерден тұратын жиынды айтады.
Қасиеттері:
А ∪ = U А ∩ = ∅
Қасиеттері:
А ∪ = U А ∩ = ∅
U
A
Слайд 10Функциялар
Функция дегеніміз – бір айнымалының өзгеруіне байланысты өзгеріп отыратын шама.
(x1,y1)∈f және (x2,y2)∈f
x1 = x2 -ден y1 = y2 шығады.
Кез келген (x,y)∈f үшін y = f(x), яғни у х-ке тәуелді функция. у-тәуелді, х-тәуелсіз айнымалы
Функция бір немесе бірнеше тәуелсіз айнымалылар арқылы тәуелді айнымалыны көрсететін формулалармен беріледі.
f = { (x,y)∈X×Y | y = f(x) }
x1 = x2 -ден y1 = y2 шығады.
Кез келген (x,y)∈f үшін y = f(x), яғни у х-ке тәуелді функция. у-тәуелді, х-тәуелсіз айнымалы
Функция бір немесе бірнеше тәуелсіз айнымалылар арқылы тәуелді айнымалыны көрсететін формулалармен беріледі.
f = { (x,y)∈X×Y | y = f(x) }
f – (x,y) жұбын анықтайтын сәйкестік
f(x) – x∈X элементіне сәйкес
y∈Y элементінің белгіленуі
Слайд 11Қатынас
Қатынас деп әр түрлі нысандар қасиетін және олардың арасындағы байланысты
анықтайтын математикалық құрылымды айтады.
(Х,R) жиындар жұбын қатынас деп атайды, мұндағы R⊆Хn.
Жиында берілетін n-орынды (n-арнды) қатынас деп, жиындардың тура көбейтіндісінің ішкі жиындары аталады
(Х,R) жиындар жұбын қатынас деп атайды, мұндағы R⊆Хn.
Жиында берілетін n-орынды (n-арнды) қатынас деп, жиындардың тура көбейтіндісінің ішкі жиындары аталады
Слайд 12 Қатынастар түрлері
Бір орынды немесе
унарлы қатынас деп бір айнымалымен орындалатын қатынасты айтады (терістеу амалы, санның дәрежесін табу).
Екі орынды қатынастарды бинарлы деп атайды және оларды инфиксті жазбамен жазады: хRу. (конъюнкция, дизъюнкция)
Үш орынды қатынастарды тренарлы деп атайды.
“Би” сөзі “екі”, “уно” сөзі “бір” деген мағынаны береді.
Екі орынды қатынастарды бинарлы деп атайды және оларды инфиксті жазбамен жазады: хRу. (конъюнкция, дизъюнкция)
Үш орынды қатынастарды тренарлы деп атайды.
“Би” сөзі “екі”, “уно” сөзі “бір” деген мағынаны береді.
Слайд 13 Қатынастар қасиеттері
Рефлексивтік
х R х - ақиқат ;
Антирефлексивтік
х R х - жалған;
Симметриялық
х
R у → у R х ;
Антисимметриялық
(х R у)&(у R х) → x=y ;
Сызықтық
Егер (х R у) – ақиқат, онда (у R х) – жалған;
Транзитивтік
(х R у)&(у R z) → x R z .
Антисимметриялық
(х R у)&(у R х) → x=y ;
Сызықтық
Егер (х R у) – ақиқат, онда (у R х) – жалған;
Транзитивтік
(х R у)&(у R z) → x R z .
Слайд 14 Граф деп өзара байланысқан нысандар жиынтығын айтады. Нысандар-шыңдар деп аталады
және нүктелер арқылы белгіленеді. Ал шыңдар арасындағы байланыс-доғалар немесе қабырғалар деп аталады
Граф G = (V, Е) V және Е соңғы жиындар жұбымен беріледі. Бірінші жиын элементтері v1, v2,..., v M графтың шыңы деп аталады (графикалық көріністе оларға нүктелер сәйкес). Екінші жиын элементтері el, e2, ..., e N қабырғалар деп аталады. Әр қабырға шыңдар жұбымен анықталады (графикалық көріністе қабырғалар графтың екі шыңын қосады).
Граф G = (V, Е) V және Е соңғы жиындар жұбымен беріледі. Бірінші жиын элементтері v1, v2,..., v M графтың шыңы деп аталады (графикалық көріністе оларға нүктелер сәйкес). Екінші жиын элементтері el, e2, ..., e N қабырғалар деп аталады. Әр қабырға шыңдар жұбымен анықталады (графикалық көріністе қабырғалар графтың екі шыңын қосады).
Графтар
Слайд 16Графтың түрлері
Егер графтың барлық қабырғалары бағытталмаған болса, онда ол бағытталмаған граф
деп, ал егер графтың барлық қабырғалары бағытталған болса, онда ол бағытталған граф деп аталады.
Егер графта бағытталған және бағытталмаған да қабырғалар болса, ол аралас граф деп аталады.
Егер граф қабырғалары шыңдардың реттелген жұбымен анықталса, онда оны бағытталған қабырға немесе доға деп атайды (сызбада бағытталған қабырғаға оның бағытын анықтайтын стрелкалар қойылады).
Егер графта бағытталған және бағытталмаған да қабырғалар болса, ол аралас граф деп аталады.
Егер граф қабырғалары шыңдардың реттелген жұбымен анықталса, онда оны бағытталған қабырға немесе доға деп атайды (сызбада бағытталған қабырғаға оның бағытын анықтайтын стрелкалар қойылады).
Слайд 17 Егер екі шың екі немесе одан да көп қабырғалармен қосылса,
онда мұндай қабырғалар параллельді деп аталады (мысалы, қабырғалар е4 және е5).
Егер қабырғаның басы мен соңы бір жерден шықса, онда мұндай қабырға ілмек (петля) деп аталады(мысалы, қабырға e7). Ілмексіз және параллельді қабырғаларсыз графтар қарапайым деп аталады.
Егер қабырғаның басы мен соңы бір жерден шықса, онда мұндай қабырға ілмек (петля) деп аталады(мысалы, қабырға e7). Ілмексіз және параллельді қабырғаларсыз графтар қарапайым деп аталады.
Графтың қасиеттері
Слайд 18 Ағаштар
Ағаш деп циклсыз бағытталмаған байланысшы графты айтады.
Орман – бұл циклсыз
кез-келген граф.
Суретте бес шыңды мүмкін ағаштар көрсетілген.
Суретте бес шыңды мүмкін ағаштар көрсетілген.
Слайд 19
Бақылау сұрақтары:
Жиын анықтамасын беріңіз?
Жиынның қандай түрлерін білесіз?
Логиканы негізін салушы кім?
Ақиқаттық
кестесі деген не?
Логиканың негізгі заңдарын атаңыз?
Граф деген не?
Ағаш деген не ?
Логиканың негізгі заңдарын атаңыз?
Граф деген не?
Ағаш деген не ?