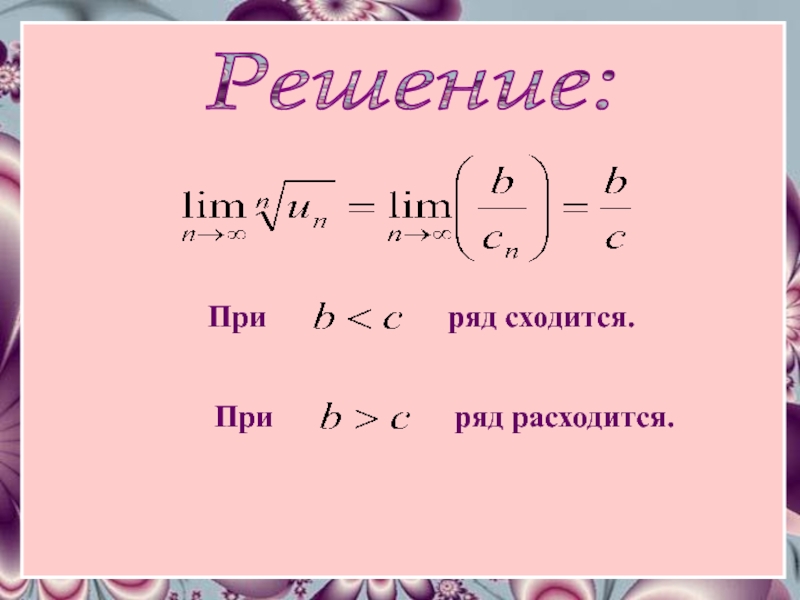Последовательность частичных сумм ряда
с неотрицательными членами является
неубывающей.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ряды с положительными членами презентация
Содержание
- 1. Ряды с положительными членами
- 2. ТЕОРЕМА 1. (необходимое и достаточное
- 3. ТЕОРЕМА 2. (признак сравнения) Пусть даны два ряда с положительными членами причем
- 4. Тогда Если сходится второй
- 5. Доказательство: 1 Пусть частичные суммы рядов
- 6. Эта последовательность является также ограниченной, т.к.
- 7. Замечание: Так как сходимость ряда не
- 8. Примеры 1 Исследовать сходимость ряда
- 9. Решение Сравним этот ряд c геометрическим
- 10. 2 Исследовать сходимость ряда
- 11. Решение Сравним этот ряд c расходящимся
- 12. Эталонные ряды, используемые для сравнения
- 13. 2 Гармонический ряд - расходится.
- 14. 3 Обобщенный гармонический ряд и расходится при сходится при
- 15. ТЕОРЕМА 3. (предельный признак сравнения)
- 16. Доказательство: Так как то по определению
- 17. Если ряд сходится, то ряд
- 18. Пример Исследовать сходимость ряда
- 19. Решение: Сравним этот ряд c гармоническим
- 20. ТЕОРЕМА 4. ( признак Даламбера)
- 21. Доказательство: По определению предела числовой последовательности
- 22. Получили, что члены ряда меньше членов геометрического ряда который сходится при q
- 23. 2 Пусть l>1. Выберем ε таким
- 24. Примеры 1 Исследовать сходимость ряда
- 25. Решение: Ряд сходится.
- 26. 2 Исследовать сходимость ряда
- 27. Решение: Ряд расходится.
- 28. ТЕОРЕМА 5. (интегральный признак сходимости)
- 29. Тогда для сходимости ряда необходимо, чтобы сходился несобственный интеграл
- 30. Доказательство: Рассмотрим ряд Его n-частичной суммой
- 31. т.к. Т.к. функция f(x) – монотонна на любом отрезке [n,n+1] или
- 32. Если ряд - сходится, то по
- 33. Пример Исследовать сходимость ряда
- 34. Решение: Пусть При x>0 эта
- 35. Если
- 36. ТЕОРЕМА 6. (признак Коши)
- 37. Доказательство: По определению предела числовой последовательности
- 38. Выберем ε таким малым, что число
- 39. Пример Исследовать сходимость ряда где
- 40. Решение: При ряд сходится. При ряд расходится.
Слайд 1
13.3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ
ЧЛЕНАМИ
Рассмотрим ряды с неотрицательными членами. Основное свойство
Слайд 2
ТЕОРЕМА 1.
(необходимое и достаточное условие
сходимости ряда)
Для того, чтобы ряд
членами сходился, необходимо и
достаточно, чтобы последовательность
его частичных сумм была ограничена.
Слайд 4
Тогда
Если сходится второй ряд, то сходится и первый;
Если расходится первый
Слайд 5
Доказательство:
1
Пусть частичные суммы рядов (1) и (2) равны, соответственно,
По условию
Рассмотрим последовательность частичных сумм
Эта последовательность является возрастающей, т.к. с ростом n увеличивается сумма положительных слагаемых.
Слайд 6
Эта последовательность является также ограниченной, т.к.
Поэтому на основании признака существования предела
2
От противного:
Предположим, что ряд (2) сходится, следовательно будет сходиться и ряд (1), что противоречит условию теоремы.
Следовательно, ряд (2) – расходится.
Слайд 7
Замечание:
Так как сходимость ряда не меняется при
отбрасывании конечного числа членов
то условие сравнения не обязательно
должно выполняться с первых членов рядов.
Достаточно, чтобы оно выполнялось,
начиная с некоторого номера k.
Слайд 9
Решение
Сравним этот ряд c геометрическим рядом
При
- ряд сходится.
Т.к. члены заданного
Слайд 11
Решение
Сравним этот ряд c расходящимся гармоническим рядом
Т.к. члены заданного ряда, начиная
Слайд 15
ТЕОРЕМА 3.
(предельный признак сравнения)
Если
ряды с положительными членами и существует конечный
то ряды одновременно сходятся или расходятся.
Слайд 16
Доказательство:
Так как
то по определению предела числовой последовательности для любого ε>0 существует
Слайд 17
Если ряд
сходится, то ряд
тоже сходится, и в силу признака сравнения
сходится ряд
Аналогично, если ряд
сходится, то ряд
тоже сходится, и
будет сходится ряд
Слайд 19
Решение:
Сравним этот ряд c гармоническим рядом
поскольку при больших n
Так как
Слайд 20
ТЕОРЕМА 4.
( признак Даламбера)
Пусть для ряда
членами существует конечный предел отношения
Если l <1 – ряд сходится; если l >1 – ряд расходится; если l=1 – вопрос о сходимости остается нерешенным.
с положительными
Слайд 21
Доказательство:
По определению предела числовой последовательности для любого ε>0 существует такой номер
1
Пусть l<1. Выберем ε таким малым, что число q=l+ε<1, т.е.
или
Это неравенство будет выполняться для всех n>N, т.е. для n=N+1, N+2…
Слайд 22
Получили, что члены ряда
меньше членов геометрического ряда
который сходится при q
тоже сходится, т.к. он отличается от рассматриваемого на первые (n+1) членов.
Слайд 23
2
Пусть l>1. Выберем ε таким малым, что
число l-ε>1, т.е.
или
Значит члены
Ряд расходится.
Слайд 28
ТЕОРЕМА 5.
(интегральный признак сходимости)
Пусть дан ряд
положительны и не возрастают, т.е.
а функция f(x), определенная при
непрерывна и не возрастает, и
Слайд 30
Доказательство:
Рассмотрим ряд
Его n-частичной суммой будет
1
Сходимость этого ряда означает, что существует предел
Слайд 32
Если ряд
- сходится, то по признаку
сравнения должен сходится и ряд (1).
тоже будет сходящимся, и наоборот.
Слайд 34
Решение:
Пусть
При x>0 эта функция положительна и не возрастающая.
Если
Т.е. интеграл
Слайд 36
ТЕОРЕМА 6.
(признак Коши)
Пусть дан ряд
положительны. Если существует предел
члены которого
то
Слайд 37
Доказательство:
По определению предела числовой последовательности для любого ε>0 существует такой номер
1
Пусть L<1.
Слайд 38
Выберем ε таким малым, что число q=L+ ε
2
Пусть L>1.
Выберем ε таким малым, что число L-ε>1, т.е. предел общего члена не может быть равен нулю и не выполняется необходимый признак сходимости.
Ряд расходится.
























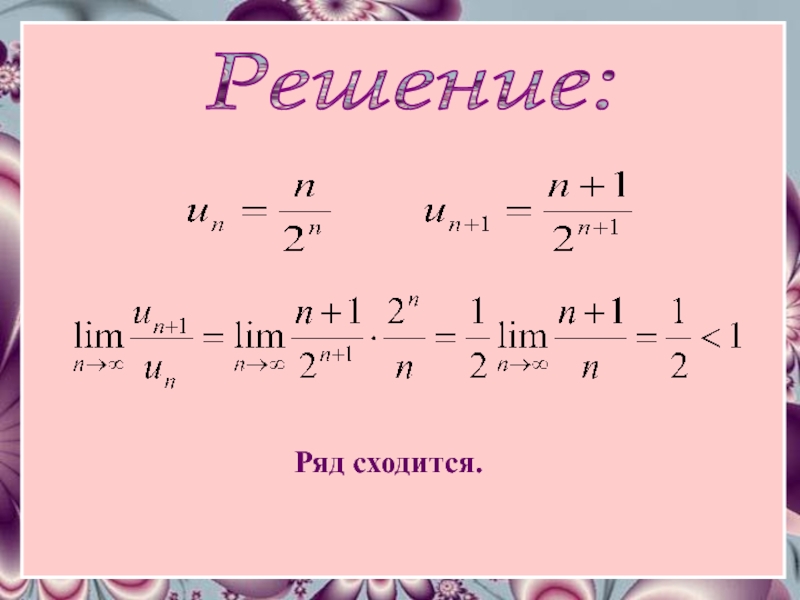





![т.к.Т.к. функция f(x) – монотонна на любом отрезке [n,n+1]или](/img/tmb/4/345985/094f27ffb5e001c4aef10cece6ed881b-800x.jpg)