- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы контурного анализа презентация
Содержание
- 1. Основы контурного анализа
- 2. Зачем нужен контурный анализ? позволяет описывать,
- 3. Основные понятия Контур – это граница объекта,
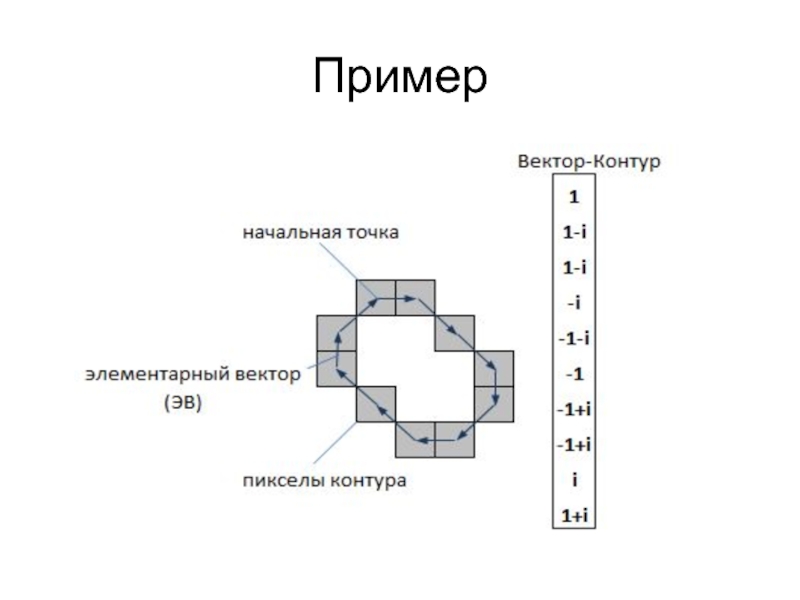
- 4. Пример
- 5. Практические задания
- 6. Основные понятия (2) Элементарный вектор Вектор-контур Вектор-контур Г длины k будем обозначать:
- 7. Свойства контуров 1. Сумма ЭВ замкнутого контура
- 8. Свойства контуров (2) 5. Изменение масштаба исходного
- 9. Скалярное произведение контуров Скалярным произведением контуров Г
- 10. Скалярное произведение контуров (2) Внимание: В контурном
- 11. Скалярное произведение контуров (3) Нормированное скалярное произведение
- 12. Скалярное произведение контуров (4) НСП в пространстве
- 13. Пример: Рассмотрим скалярное умножение контура самого на себя, но повернутого на определенный угол.
- 14. Выводы контурного анализа Модуль нормированного скалярного произведения
- 15. Выводы контурного анализа (2) Модуль дает меру
- 16. Недостаток НСП Выбор начальной точки Если контуры
- 17. Практические задания
Зачем нужен контурный анализ? позволяет описывать, хранить, сравнивать и производить поиск объектов (по контурам) рассмотрение только контуров позволяет снизить вычислительную и алгоритмическую сложность методы контурного анализа инвариантны к некоторым преобразованиям
Слайд 2Зачем нужен контурный анализ?
позволяет описывать, хранить, сравнивать и производить поиск
объектов (по контурам)
рассмотрение только контуров позволяет снизить вычислительную и алгоритмическую сложность
методы контурного анализа инвариантны к некоторым преобразованиям (перенос, поворот и изменение масштаба)
рассмотрение только контуров позволяет снизить вычислительную и алгоритмическую сложность
методы контурного анализа инвариантны к некоторым преобразованиям (перенос, поворот и изменение масштаба)
Слайд 3Основные понятия
Контур – это граница объекта, совокупность точек (пикселов), отделяющих объект
от фона.
Контур кодируется последовательностью, состоящей из комплексных чисел.
Начальная точка.
Вектор смещения
Контур кодируется последовательностью, состоящей из комплексных чисел.
Начальная точка.
Вектор смещения
Слайд 6Основные понятия (2)
Элементарный вектор
Вектор-контур
Вектор-контур Г длины k будем обозначать:
Слайд 7Свойства контуров
1. Сумма ЭВ замкнутого контура равна нулю.
2. Контур-вектор не зависит
от параллельного переноса исходного изображения.
3. Поворот изображения на определенный угол равносилен повороту каждого ЭВ контура на тот же угол.
4. Изменение начальной точки ведет к циклическому сдвигу ВК.
3. Поворот изображения на определенный угол равносилен повороту каждого ЭВ контура на тот же угол.
4. Изменение начальной точки ведет к циклическому сдвигу ВК.
Слайд 8Свойства контуров (2)
5. Изменение масштаба исходного изображения можно рассматривать как умножение
каждого ЭВ контура на масштабный коэффициент.
Слайд 9Скалярное произведение контуров
Скалярным произведением контуров Г и N называется такое комплексное
число:
Где k – размерность ВК,
γn — n-й элементарный вектор контура Г,
νn — n-й ЭВ контура N.
(γn, νn) — скалярное произведение комплексных чисел, вычисляемое как
Где k – размерность ВК,
γn — n-й элементарный вектор контура Г,
νn — n-й ЭВ контура N.
(γn, νn) — скалярное произведение комплексных чисел, вычисляемое как
Слайд 10Скалярное произведение контуров (2)
Внимание: В контурном анализе допускается скалярное произведение только
ВК одинаковой размерности.
Свойства скалярного произведения позволяют использовать его как определенную меру близости векторов.
Свойства скалярного произведения позволяют использовать его как определенную меру близости векторов.
Слайд 11Скалярное произведение контуров (3)
Нормированное скалярное произведение
Где |Г| и |N| — нормы(длины)
контуров, вычисляемые как:
Слайд 12Скалярное произведение контуров (4)
НСП в пространстве комплексных чисел, также является комплексным
числом.
Модуль НСП достигает максимального значение – единицы, только если контур Г является тем же контуром N, но повернутым на некоторый угол и промасштабированный на определенный коэффициент
Модуль НСП достигает максимального значение – единицы, только если контур Г является тем же контуром N, но повернутым на некоторый угол и промасштабированный на определенный коэффициент
Слайд 13Пример:
Рассмотрим скалярное умножение контура самого на себя, но повернутого на определенный
угол.
Слайд 14Выводы контурного анализа
Модуль нормированного скалярного произведения контуров даст единицу только в
том случае, если эти два контура равны с точностью до поворота и масштаба.
В противном случае, модуль НСП будет строго меньше единицы.
В противном случае, модуль НСП будет строго меньше единицы.
Слайд 15Выводы контурного анализа (2)
Модуль дает меру сходства контуров
Аргумент НСП –угол поворота
контуров относительно друг друга.
Слайд 16Недостаток НСП
Выбор начальной точки
Если контуры одинаковы, но отсчет ЭВ начинается с
другой начальной точки, то модуль НСП таких контуров не будет равен единице.
