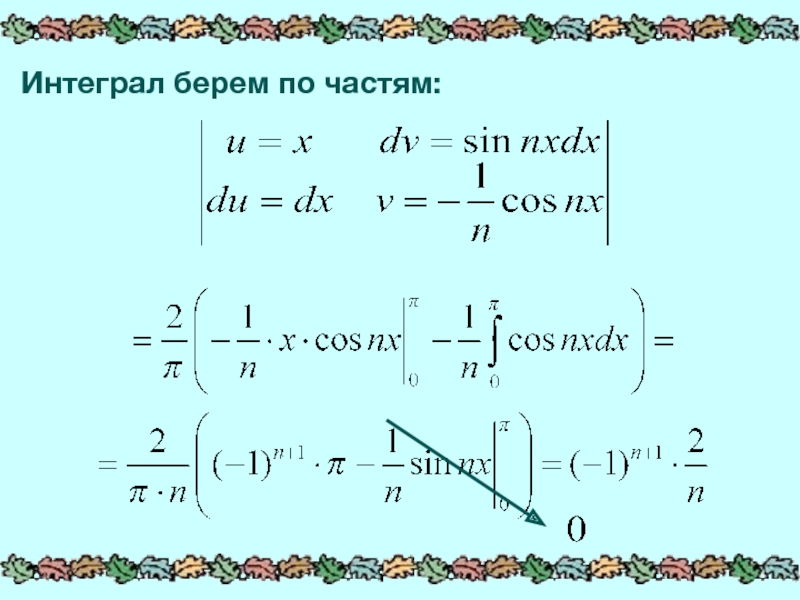возможно для функций, удовлетворяющих условию теоремы, сформулированной в предыдущем параграфе.
Для четных и нечетный функций разложение в ряд Фурье существенно упрощается.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ряды Фурье для четных и нечетных функций презентация
Содержание
- 1. Ряды Фурье для четных и нечетных функций
- 2. Пусть функция f(x) определена и является нечетной на отрезке [-П,П]: Найдем коэффициенты разложения:
- 3. В первом интеграле делаем замену:
- 4. Тогда
- 6. Таким образом, нечетная на отрезке [-П,П] функция
- 7. Пусть функция f(x) определена и является четной на отрезке [-П,П]: Найдем коэффициенты разложения:
- 8. В первом интеграле делаем замену:
- 9. Тогда
- 11. Таким образом, четная на отрезке [-П,П] функция
- 12. ПРИМЕРЫ. 1 Разложить в ряд Фурье функцию
- 13. РЕШЕНИЕ. Данная функция удовлетворяет всем условиям теоремы
- 14. Интеграл берем по частям:
- 15. Тогда ряд Фурье для данной функции будет иметь вид:
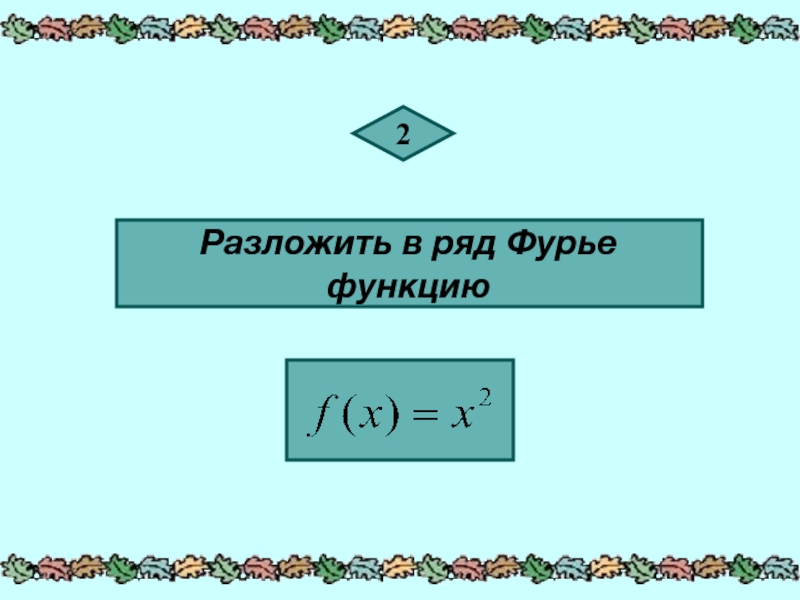
- 16. 2 Разложить в ряд Фурье функцию
- 17. РЕШЕНИЕ. Данная функция удовлетворяет всем условиям теоремы
- 18. При n=1, 2, 3…: Интеграл берем по частям:
- 19. Оставшийся интеграл снова берем по частям:
- 20. Тогда ряд Фурье для данной функции будет иметь вид:
Слайд 2Пусть функция f(x) определена и является нечетной на отрезке [-П,П]:
Найдем коэффициенты
разложения:
Слайд 6Таким образом, нечетная на отрезке
[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим
образом:
Слайд 7Пусть функция f(x) определена и является четной на отрезке [-П,П]:
Найдем коэффициенты
разложения:
Слайд 11Таким образом, четная на отрезке
[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим
образом:
Слайд 13РЕШЕНИЕ.
Данная функция удовлетворяет всем условиям теоремы о разложении функции в ряд
Фурье.
Она является нечетной на отрезке [-П,П], поэтому
Она является нечетной на отрезке [-П,П], поэтому
Слайд 17РЕШЕНИЕ.
Данная функция удовлетворяет всем условиям теоремы о разложении функции в ряд
Фурье.
Она является четной на отрезке [-П,П], поэтому
Она является четной на отрезке [-П,П], поэтому
При n=0:

![Пусть функция f(x) определена и является нечетной на отрезке [-П,П]:Найдем коэффициенты разложения:](/img/tmb/5/449261/b617619d6a82b6a8ba976c6d9acd0d69-800x.jpg)

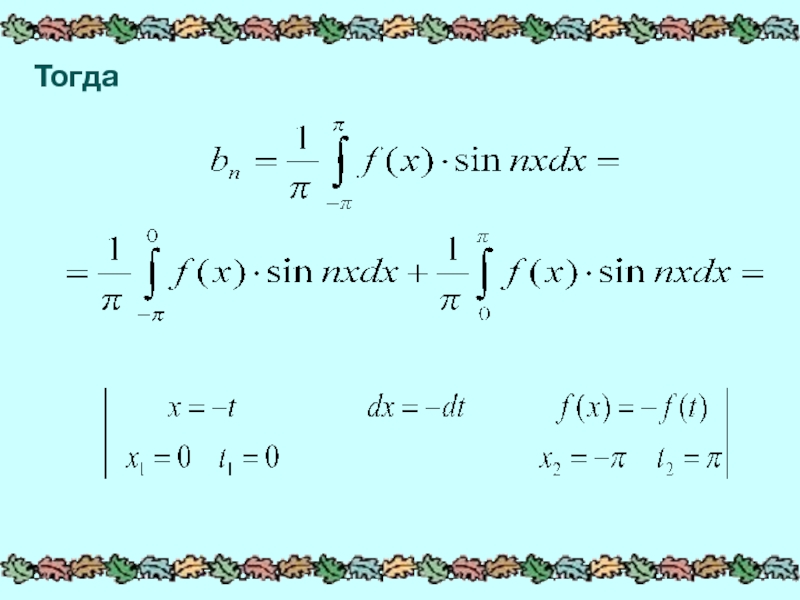
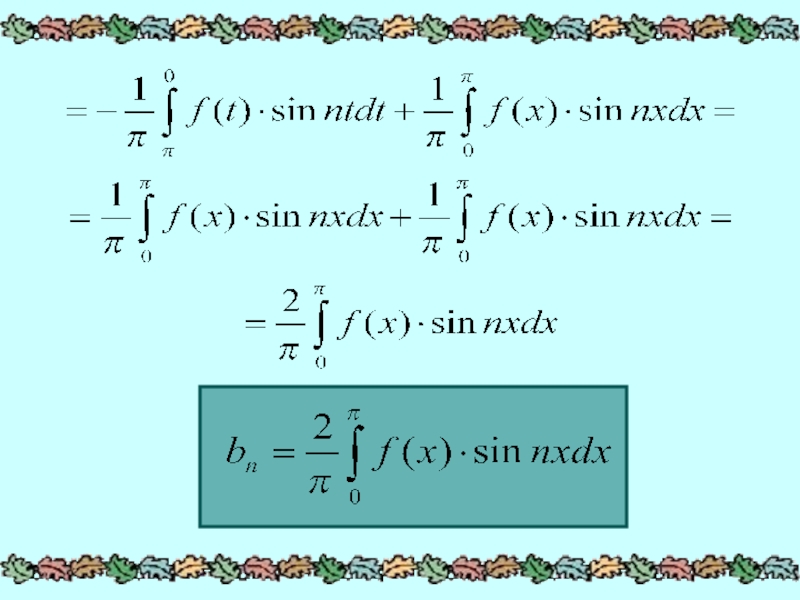
![Таким образом, нечетная на отрезке[-П,П] функция f(x) будетразлагаться в ряд Фурьеследующим образом:](/img/tmb/5/449261/2076433c8595368e31d7e690cd18e39b-800x.jpg)
![Пусть функция f(x) определена и является четной на отрезке [-П,П]:Найдем коэффициенты разложения:](/img/tmb/5/449261/10a5f4feec7bba98994ec62df5e97158-800x.jpg)

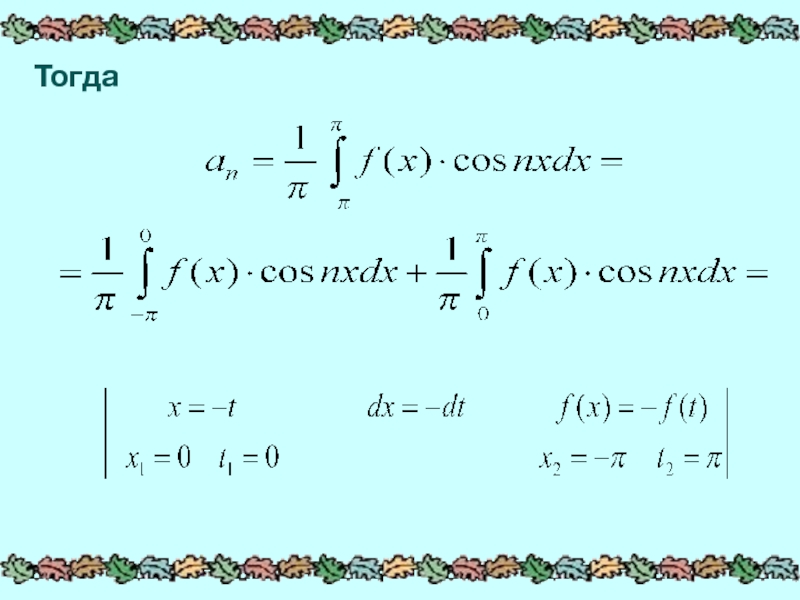
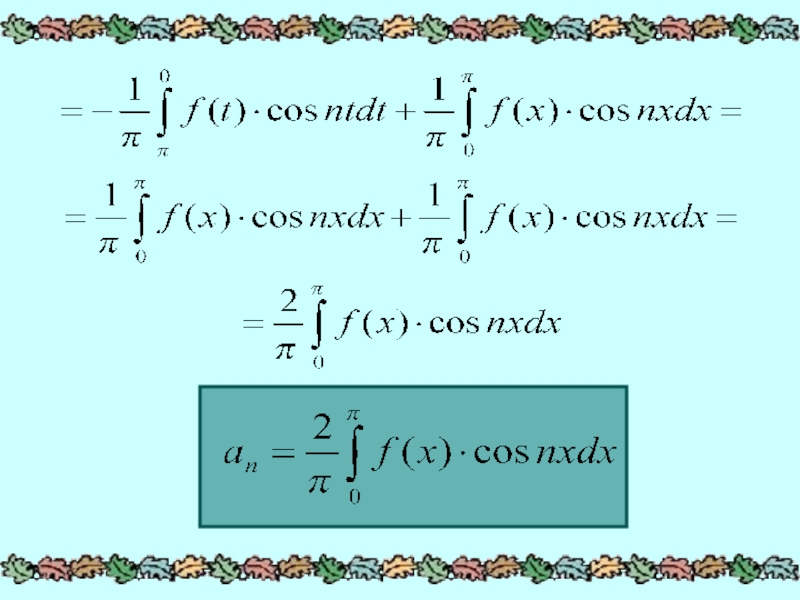
![Таким образом, четная на отрезке[-П,П] функция f(x) будетразлагаться в ряд Фурьеследующим образом:](/img/tmb/5/449261/6f647ca48c6ff155fe27300a51cd84af-800x.jpg)