- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Розрахунок надійності системи. Розрахунок заданої системи. Побудова діагностичної моделі об’єкту презентация
Содержание
- 1. Розрахунок надійності системи. Розрахунок заданої системи. Побудова діагностичної моделі об’єкту
- 2. 1. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ 1.1 Розрахунок заданої
- 3. 1. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ 1.1 Розрахунок заданої
- 4. 1. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ 1.2 Підвищення показників
- 5. 1. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ 1.2 Підвищення показників
- 6. 1. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ 1.3 Підвищення показників
- 7. 1. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ 1.4 Розрахунок вартості
- 8. 2. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ Структурна схема
- 9. 2. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ Користуючись схемою
- 10. 2. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ З системи
- 11. 2. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ Підставляючи значення
Слайд 11. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.1 Розрахунок заданої системи
Структурна схема надійності
Перетворена місткова схема
Приступимо
Слайд 21. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.1 Розрахунок заданої системи
Перетворена місткова схема
Елементи 10, 11,
Слайд 31. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.1 Розрахунок заданої системи
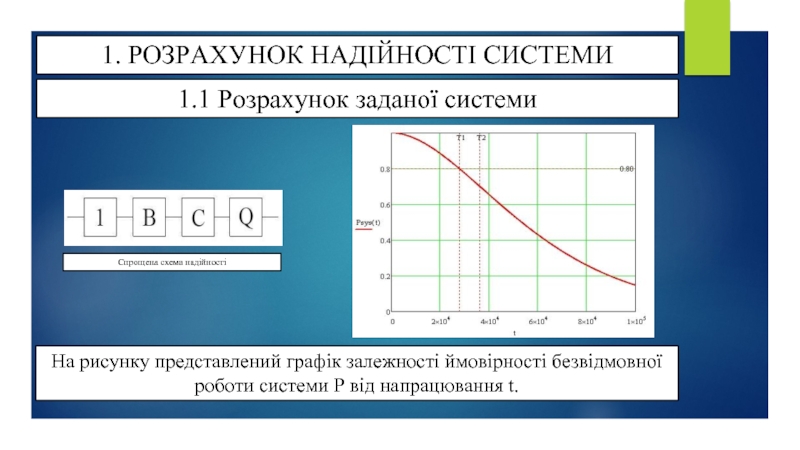
Спрощена схема надійності
На рисунку представлений
Слайд 41. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.2 Підвищення показників надійності системи шляхом підвищення надійності
Порахуємо значення ймовірностей безвідмовної роботи кожного квазі-елементу в час Т2.
Як бачимо, зі всіх квазіелементів в час Т2, Pc має найменше значення ймовірності безвідмовної роботи. Значить треба підвищити надійність елементів саме цього квазіелементу схеми.
Для забезпечення необхідної надійності схеми в час Т2, обчислимо нове значення ймовірності безвідмовної роботи 3-го квазіелементу в час Т2:
Слайд 51. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.2 Підвищення показників надійності системи шляхом підвищення надійності
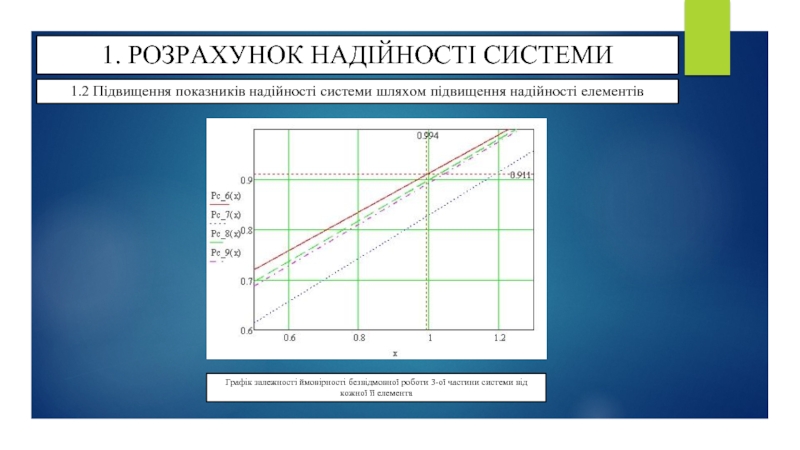
Графік залежності ймовірності безвідмовної роботи 3-ої частини системи від кожної її елемента
Слайд 61. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.3 Підвищення показників надійності системи шляхом зміни структури
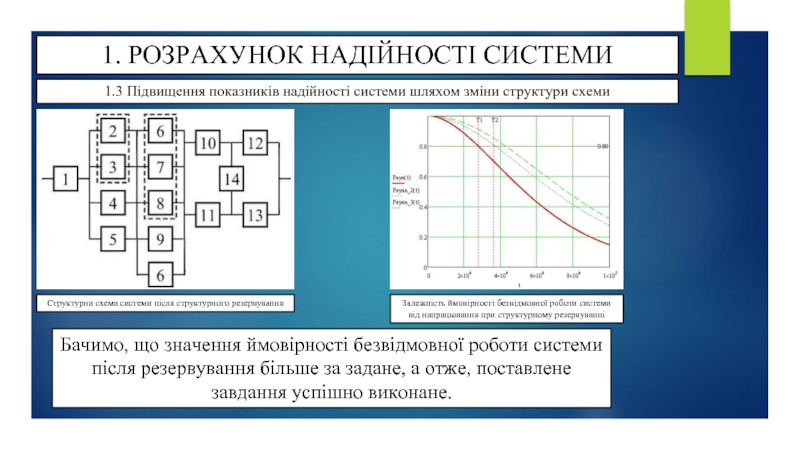
Структурна схема системи після структурного резервування
Залежність ймовірності безвідмовної роботи системи від напрацювання при структурному резервуванні
Бачимо, що значення ймовірності безвідмовної роботи системи після резервування більше за задане, а отже, поставлене завдання успішно виконане.
Слайд 71. РОЗРАХУНОК НАДІЙНОСТІ СИСТЕМИ
1.4 Розрахунок вартості варіантів модернізованих систем
(5.4+6.1+1.4+9.8+3.3+0.8+5.5+5.1+3.6+6.6+8.5+6.6+4.5+5.7+1.3) = 74.2
Розрахуємо вартість системи при підвищенні надійності елементів. Якщо інтенсивність відмови 6-го та 8-го елементів складає 0.4 від початкової, то ціна буде складати 1.6 початкової, а якщо інтенсивність відмови 9-го елемента складає 0.8 від початкової, то ціна буде складати 1.2 початкової
(5.4+6.1+1.4+9.8+3.3+0.8*1.6+5.5+5.1*1.6+3.6*1.2+6.6+8.5+6.6+4.5+5.7+1.3) = 78.46 тис. грн.
Тепер розрахуємо вартість системи при структурному резервуванні
(5.4+6.1+1.4+9.8+3.3+0.8*2+5.5+5.1+3.6+6.6+8.5+6.6+4.5+5.7+1.3) = 75 тис. грн.
Слайд 82. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ
Структурна схема системи
Для побудови діагностичної моделі об'єкту
Слайд 92. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ
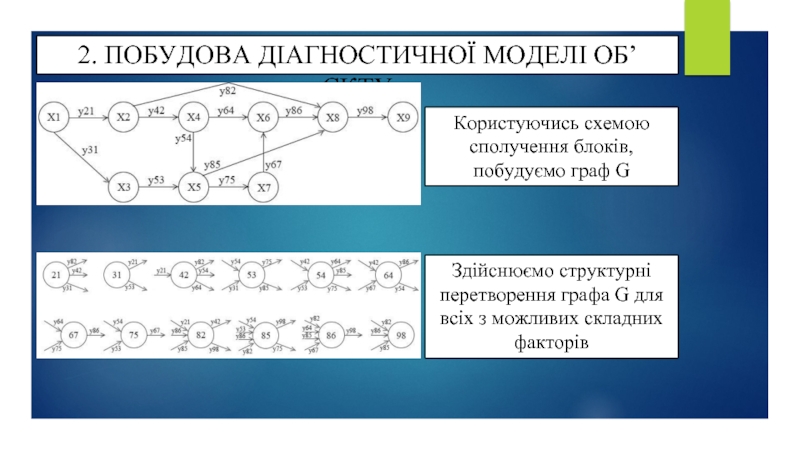
Користуючись схемою сполучення блоків, побудуємо граф G
Здійснюємо
Слайд 102. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ
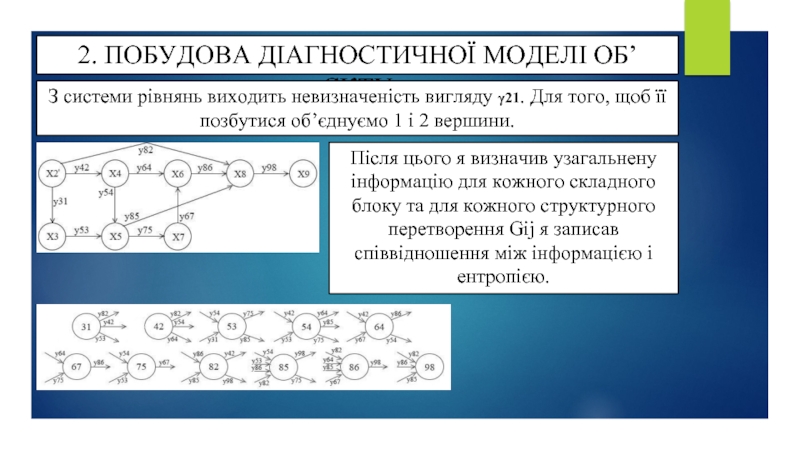
З системи рівнянь виходить невизначеність вигляду γ21.
Після цього я визначив узагальнену інформацію для кожного складного блоку та для кожного структурного перетворення Gij я записав співвідношення між інформацією і ентропією.
Слайд 112. ПОБУДОВА ДІАГНОСТИЧНОЇ МОДЕЛІ ОБ’ЄКТУ
Підставляючи значення функціоналів інформації і ентропію для
Ми отримали систему з 11 лінійних алгебраїчних рівнянь, яка побудована з використанням графа G2’. Вона розглядається як адекватна діагностична модель, яка відповідає об’єкту.