- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр презентация
Содержание
- 1. Решение задач разными способами. Свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр
- 2. ЗАДАЧА На боковой стороне АВ равнобедренного
- 3. РЕШЕНИЕ. (свойство равнобедренного треугольника, свойство вписанного угла,
- 4. 1. Найдем сторону СМ треугольника MNC.
- 5. Способ А По свойству отрезков секущих.
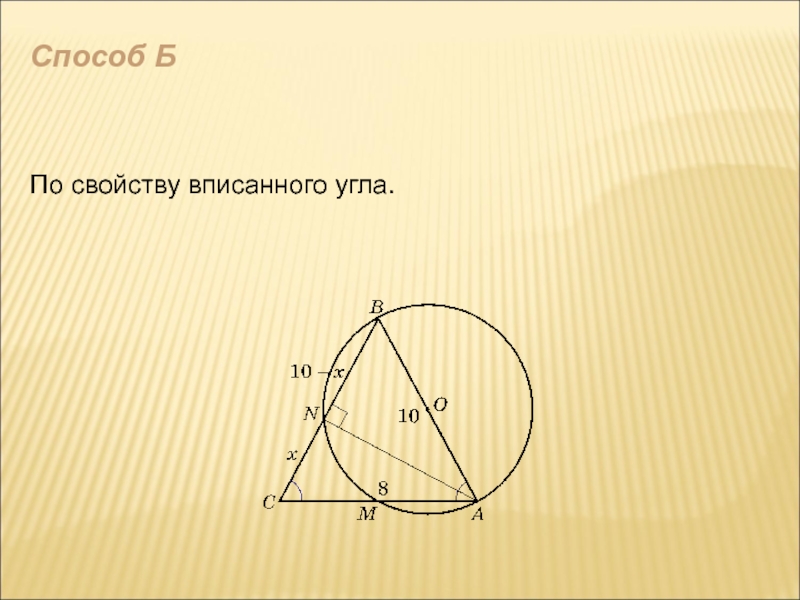
- 6. Способ Б По свойству вписанного угла.
- 7. Способ В С помощью теоремы Пифагора.
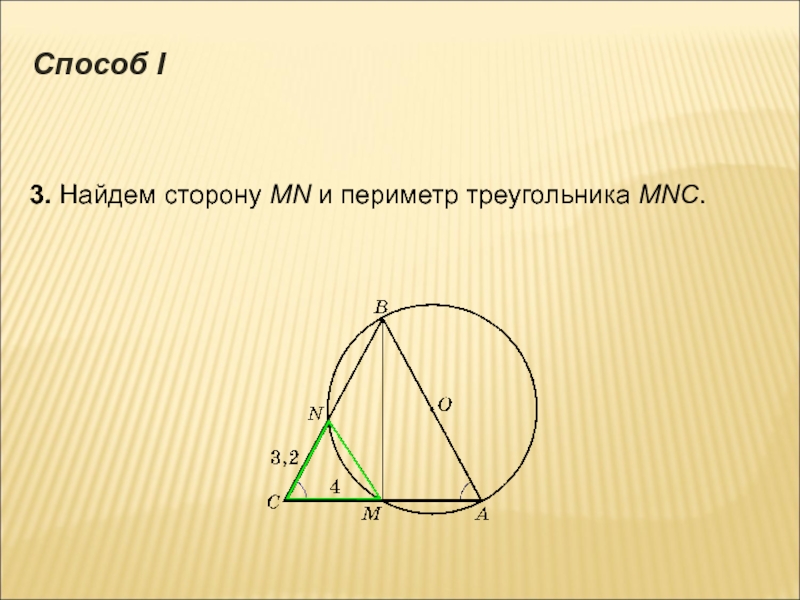
- 8. 3. Найдем сторону МN и периметр треугольника MNC. Способ I
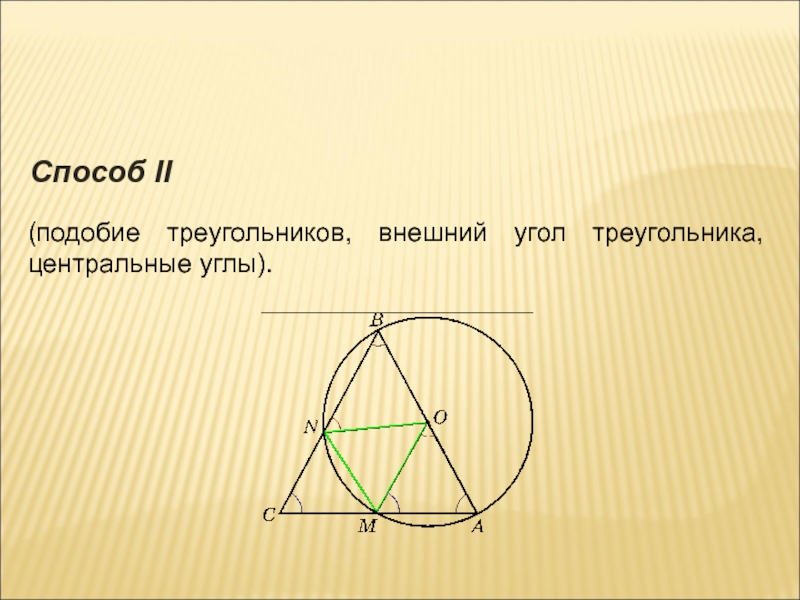
- 9. (подобие треугольников, внешний угол треугольника, центральные углы). Способ II
- 10. (средняя линия треугольника, теорема Фалеса, свойства параллельных
ЗАДАЧА На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М и боковую сторону СВ в точке N. Найдите периметр треугольника MNC,
Слайд 2ЗАДАЧА
На боковой стороне АВ равнобедренного треугольника как на диаметре построена
окружность. Окружность пересекает основание АС в точке М и боковую сторону СВ в точке N. Найдите периметр треугольника MNC, если АВ = 10, АС = 8.
Слайд 3РЕШЕНИЕ.
(свойство равнобедренного треугольника, свойство вписанного угла, опирающегося на диаметр, свойство отрезков
секущих, теорема Пифагора).
Способ I
Слайд 41. Найдем сторону СМ треугольника MNC.
2. Найдем сторону СN треугольника MNC. Это
можно сделать несколькими способами.
Способ I
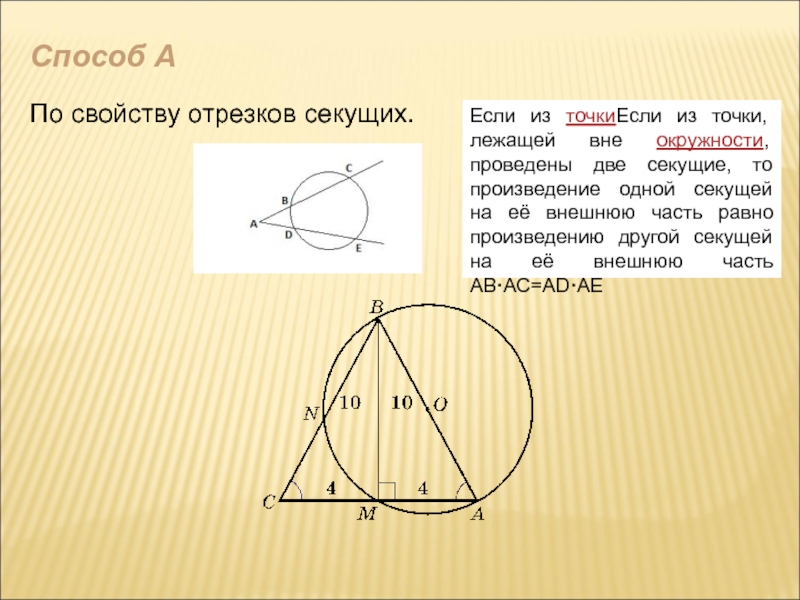
Слайд 5Способ А
По свойству отрезков секущих.
Если из точкиЕсли из точки, лежащей
вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть АВ·АС=АD·АЕ
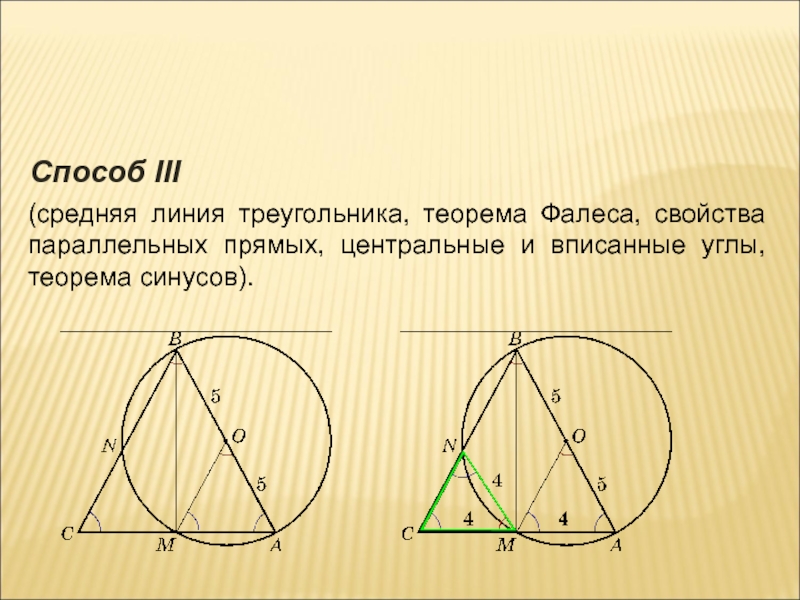
Слайд 10(средняя линия треугольника, теорема Фалеса, свойства параллельных прямых, центральные и вписанные
углы, теорема синусов).
Способ III
