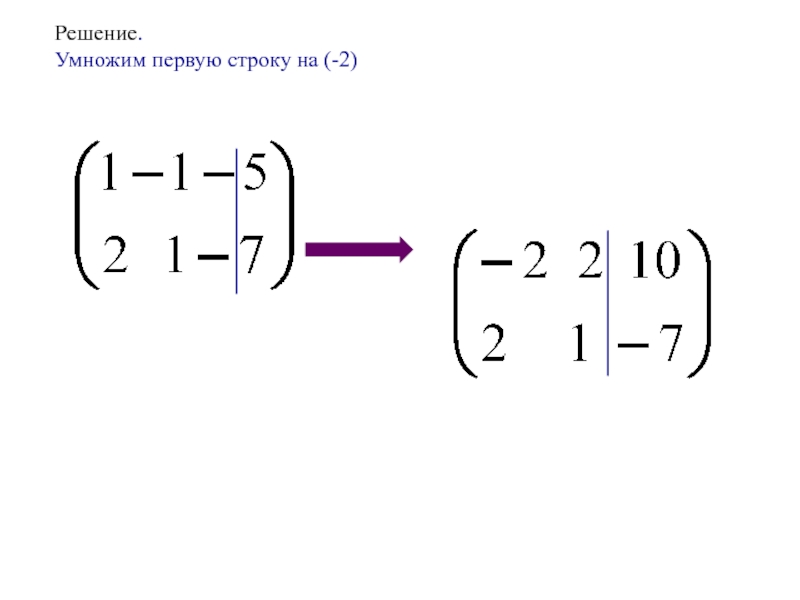Решение систем линейных уравнений методом Гаусса презентация

Содержание

1. Решение систем линейных уравнений методом Гаусса
2. Метод Гаусса – это метод последовательного исключения
3. При выполнении прямого хода используют следующие преобразования:
4. Решить систему уравнений методом Гаусса
5. Матрица системы – это матрица, составленная только
6. Решение. Умножим первую строку на (-2)
7. ко второй строке прибавим первую строку умноженную на -2
8. Разделим опять первую строку на (-2) строка,
9. Цель элементарных преобразований – привести матрицу к ступенчатому
10. В результате элементарных преобразований получена эквивалентная исходной система уравнений
11. Решить систему уравнений методом Гаусса Решение.
12. Чтобы в первом столбце получить а2=а3=0, умножим
13. Разделим 2-ю строку на 8, полученные результаты
14. Запишем новую эквивалентную систему с учетом расширенной

Метод Гаусса – это метод последовательного исключения переменных Систему уравнений приводят к эквивалентной ей системе с треугольной матрицей. Это называется прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных

Главная
Математика
Решение систем линейных уравнений методом Гаусса

Слайд 1Решение систем линейных уравнений методом Гаусса

Слайд 2Метод Гаусса – это метод последовательного исключения переменных
Систему уравнений приводят к

эквивалентной ей системе с треугольной матрицей. Это называется прямым ходом.
Из полученной треугольной системы переменные находят с помощью последовательных подстановок. Это называется обратным ходом.

Слайд 3При выполнении прямого хода используют следующие преобразования:
Умножение или деление коэффициентов свободных

членов на одно и то же число;
Сложение и вычитание уравнений;
Перестановка уравнений системы;
Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.

Слайд 4Решить систему уравнений методом Гаусса

Нужно записать расширенную матрицу системы

Вертикальная черта внутри матрицы

не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Слайд 5
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.

Расширенная матрица

системы – это та же матрица системы плюс столбец свободных членов, в данном случае.

Слайд 6Решение. Умножим первую строку на (-2)

Слайд 7ко второй строке прибавим первую строку умноженную на -2

Слайд 8Разделим опять первую строку на (-2)
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К

КОТОРОЙ ПРИБАВЛЯЮТ.

Слайд 9Цель элементарных преобразований –
привести матрицу к ступенчатому виду. Сам термин «ступенчатый вид»

не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный

Слайд 10В результате элементарных преобразований получена эквивалентная исходной система уравнений
Выполняем обратный ход, т.е.

подстановку в первое уравнение вместо у,
х =-5+у
х=-5+1
х=-4
Ответ: (-4; 1)

Слайд 11Решить систему уравнений методом Гаусса
Решение.

Переставим третье уравнение на место первого и

запишем расширенную матрицу:

Слайд 12Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на

3, а затем на 2 и вычтем результаты из 2-й и 3-й строк

Слайд 13Разделим 2-ю строку на 8, полученные результаты умножим на 3 и

вычтем из 3-й строки

Слайд 14Запишем новую эквивалентную систему с учетом расширенной матрицы
Выполняем обратный ход, с

помощью последовательных подстановок находим неизвестные

Ответ: (1; 2; 3)

Скачать презентацию

Решение систем линейных уравнений методом Гаусса презентация

Содержание

Слайд 1Решение систем линейных уравнений методом Гаусса

Слайд 2Метод Гаусса – это метод последовательного исключения переменных
Систему уравнений приводят к

Слайд 3При выполнении прямого хода используют следующие преобразования:
Умножение или деление коэффициентов свободных

Слайд 4Решить систему уравнений методом Гаусса

Нужно записать расширенную матрицу системы

Вертикальная черта внутри матрицы

Слайд 5
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.

Расширенная матрица

Слайд 6Решение. Умножим первую строку на (-2)

Слайд 7ко второй строке прибавим первую строку умноженную на -2

Слайд 8Разделим опять первую строку на (-2)
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К

Слайд 9Цель элементарных преобразований –
привести матрицу к ступенчатому виду. Сам термин «ступенчатый вид»

Слайд 10В результате элементарных преобразований получена эквивалентная исходной система уравнений
Выполняем обратный ход, т.е.

Слайд 11Решить систему уравнений методом Гаусса
Решение.

Переставим третье уравнение на место первого и

Слайд 12Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на

Слайд 13Разделим 2-ю строку на 8, полученные результаты умножим на 3 и

Слайд 14Запишем новую эквивалентную систему с учетом расширенной матрицы
Выполняем обратный ход, с

Обратная связь

Что такое ThePresentation.ru?

Решение систем линейных уравнений методом Гаусса презентация

Содержание

Слайд 1Решение систем линейных уравнений методом Гаусса

Слайд 2Метод Гаусса – это метод последовательного исключения переменныхСистему уравнений приводят к

Слайд 3При выполнении прямого хода используют следующие преобразования: Умножение или деление коэффициентов свободных

Слайд 4Решить систему уравнений методом ГауссаНужно записать расширенную матрицу системыВертикальная черта внутри матрицы

Слайд 5Матрица системы – это матрица, составленная только из коэффициентов при неизвестных. Расширенная матрица

Слайд 6Решение. Умножим первую строку на (-2)

Слайд 7ко второй строке прибавим первую строку умноженную на -2

Слайд 8Разделим опять первую строку на (-2)строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К

Слайд 9Цель элементарных преобразований – привести матрицу к ступенчатому виду. Сам термин «ступенчатый вид»

Слайд 10В результате элементарных преобразований получена эквивалентная исходной система уравнений Выполняем обратный ход, т.е.

Слайд 11Решить систему уравнений методом ГауссаРешение.Переставим третье уравнение на место первого и

Слайд 12Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на

Слайд 13Разделим 2-ю строку на 8, полученные результаты умножим на 3 и

Слайд 14Запишем новую эквивалентную систему с учетом расширенной матрицыВыполняем обратный ход, с

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2Метод Гаусса – это метод последовательного исключения переменных
Систему уравнений приводят к

Слайд 3При выполнении прямого хода используют следующие преобразования:
Умножение или деление коэффициентов свободных

Слайд 4Решить систему уравнений методом Гаусса

Нужно записать расширенную матрицу системы

Вертикальная черта внутри матрицы

Слайд 5
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.

Расширенная матрица

Слайд 8Разделим опять первую строку на (-2)
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К

Слайд 9Цель элементарных преобразований –
привести матрицу к ступенчатому виду. Сам термин «ступенчатый вид»

Слайд 10В результате элементарных преобразований получена эквивалентная исходной система уравнений
Выполняем обратный ход, т.е.

Слайд 11Решить систему уравнений методом Гаусса
Решение.

Переставим третье уравнение на место первого и

Слайд 14Запишем новую эквивалентную систему с учетом расширенной матрицы
Выполняем обратный ход, с