- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение простейших тригонометрических уравнений презентация
Содержание
- 1. Решение простейших тригонометрических уравнений
- 2. * Чтобы успешно решать простейшие тригонометрические
- 3. Арксинусом числа а называют такое
- 4. Решим при помощи числовой окружности уравнение sin
- 5. Решим при помощи числовой окружности уравнение sin
- 6. Решим при помощи числовой окружности уравнение sin
- 7. Решим при помощи числовой окружности уравнение sin
- 8. П 0 arccos а Арккосинусом
- 9. Решим при помощи числовой окружности уравнение cos
- 10. Решим при помощи числовой окружности уравнение cos
- 11. Решим при помощи числовой окружности уравнение cos
- 12. Решим при помощи числовой окружности уравнение cos t=a. 4) IаI
- 13. Арктангенсом числа а называют такое число из
- 14. *
- 15. у х 0 1 П 0
- 16. *
- 17. Наша задача: свести любое тригонометрическое уравнение к простейшему виду.
- 18. Примеры уравнений. Уравнение уже имеет
- 19. Характерная ошибка Учащиеся делят обе части на 4 и получают следующее: Грубая ошибка.
- 20. Уравнение переносом слагаемого и делением обеих
- 21. О: Уравнение уже имеет простейший
- 22. О: Уравнение уже имеет простейший
- 23. О: Здесь уместно использовать формулу косинуса разности
- 24. 1 вариант 2 вариант Потренируйся.
- 25. Спасибо за то, что стараешься!
Слайд 2*
Чтобы успешно решать простейшие тригонометрические
уравнения необходимо следующее:
2) уметь определять
тангенса и котангенса для точек числовой
окружности;
4) знать понятие арксинуса, арккосинуса,
арктангенса, арккотангенса и уметь отмечать их
на числовой окружности.
1) уметь отмечать точки на числовой
окружности;
3) знать свойства основных
тригонометрических функций;
Слайд 3Арксинусом числа
а называют такое число из отрезка
[- П/2;
arcsin а
П/2
- П/2
а
arcsin (-a)=-arcsin a
-а
-arcsin а
Арксинус и решение уравнений sin t=a.
Слайд 4Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
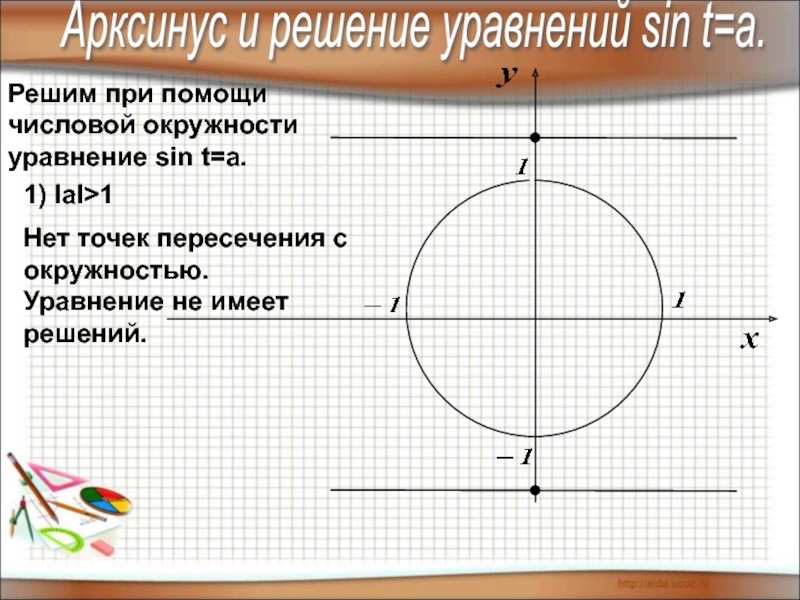
1)
Нет точек пересечения с окружностью.
Уравнение не имеет решений.
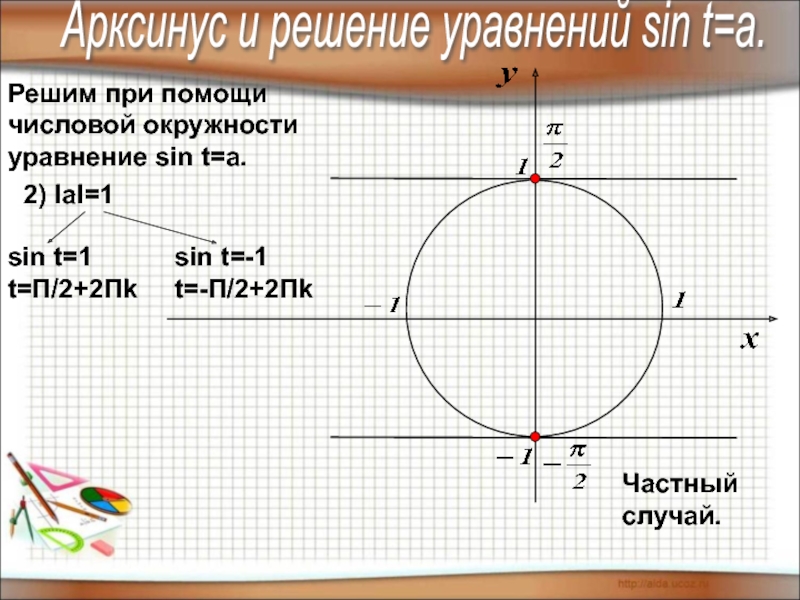
Слайд 5Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
2)
sin t=1
t=П/2+2Пk
sin t=-1
t=-П/2+2Пk
Частный случай.
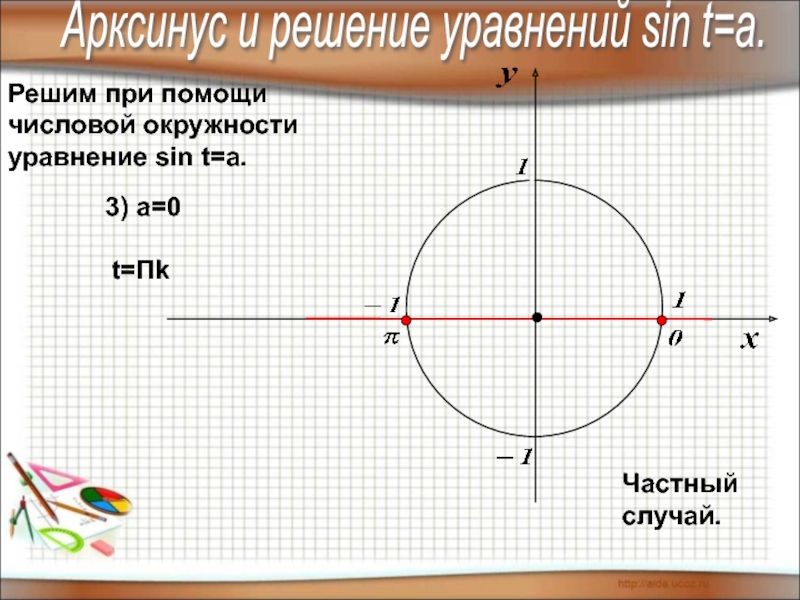
Слайд 6Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
3)
t=Пk
Частный случай.
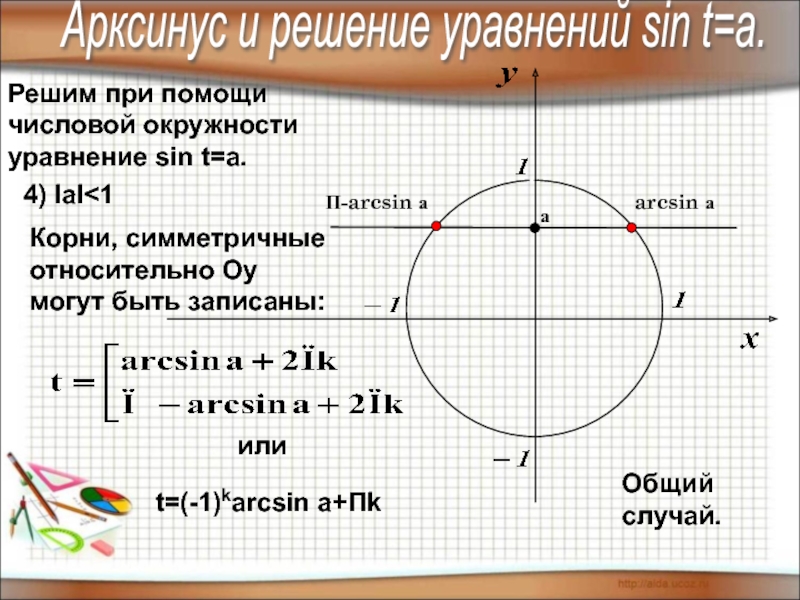
Слайд 7Решим при помощи
числовой окружности
уравнение sin t=a.
Арксинус и решение уравнений sin t=a.
4)
Общий случай.
arcsin а
П-arcsin а
Корни, симметричные относительно Оу могут быть записаны:
t=(-1)karcsin a+Пk
или
а
Слайд 8П
0
arccos а
Арккосинусом числа а называют такое число из промежутка
[0;П
а
arccos (-a)=-П-arccos a
-а
П-arccos a
Арккосинус и решение уравнений соs t=a.
Слайд 9Решим при помощи
числовой окружности
уравнение cos t=a.
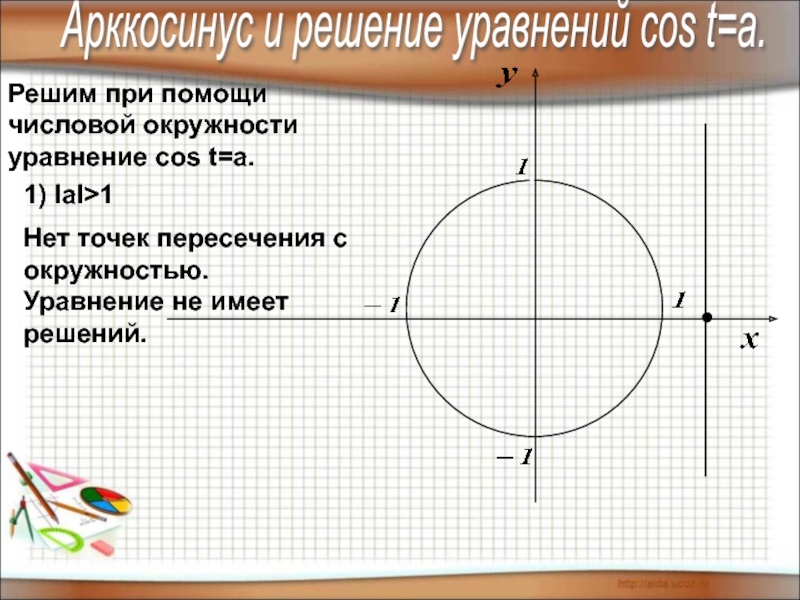
1) IаI>1
Нет точек пересечения с окружностью.
Уравнение
Арккосинус и решение уравнений соs t=a.
Слайд 10Решим при помощи
числовой окружности
уравнение cos t=a.
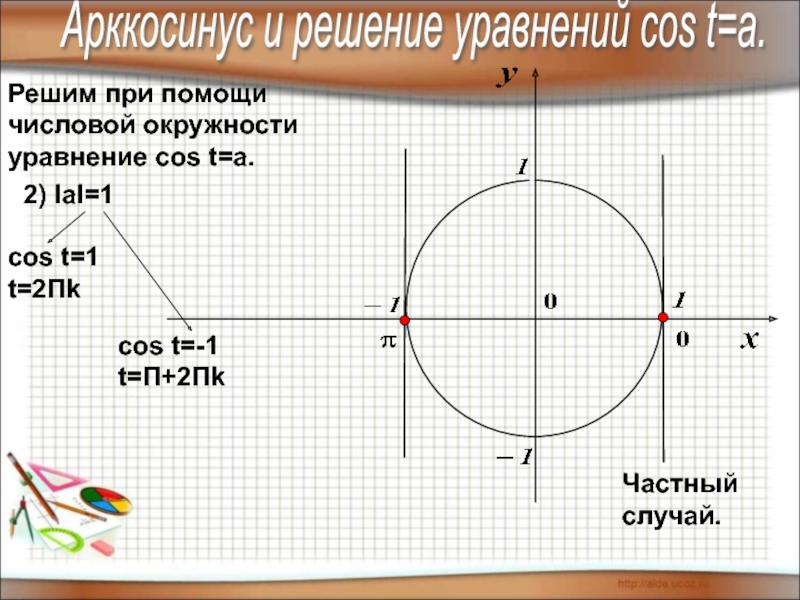
2) IаI=1
cos t=1
t=2Пk
cos t=-1
t=П+2Пk
Частный случай.
Арккосинус и
Слайд 11Решим при помощи
числовой окружности
уравнение cos t=a.
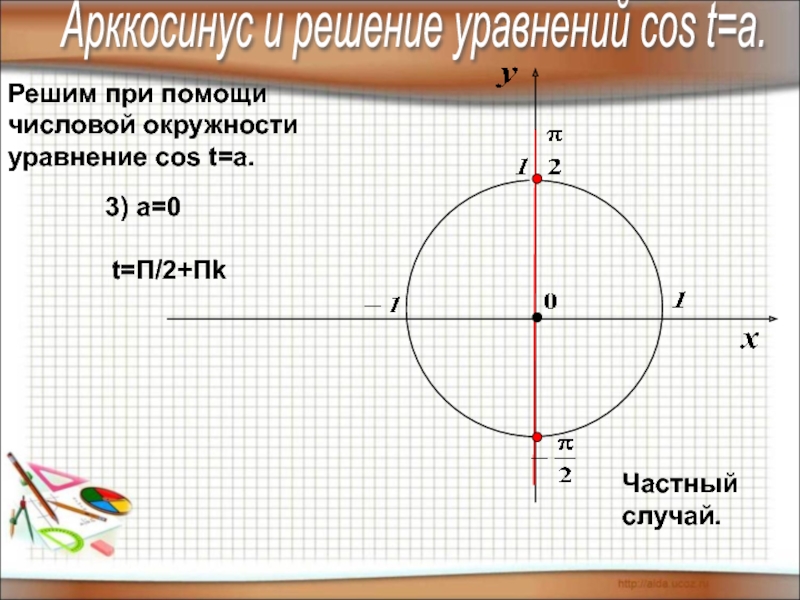
3) а=0
t=П/2+Пk
Частный случай.
Арккосинус и решение уравнений
Слайд 12Решим при помощи
числовой окружности
уравнение cos t=a.
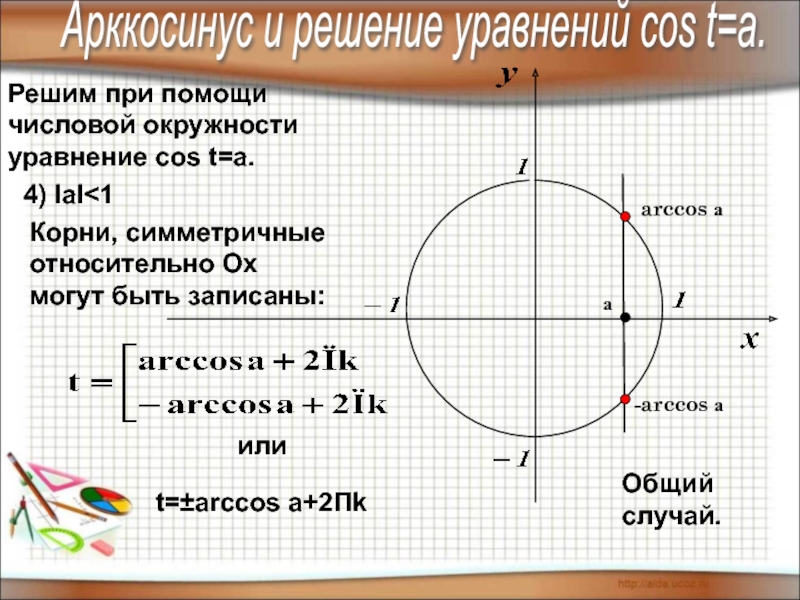
4) IаI
t=±arccos a+2Пk
или
а
Арккосинус и решение уравнений соs t=a.
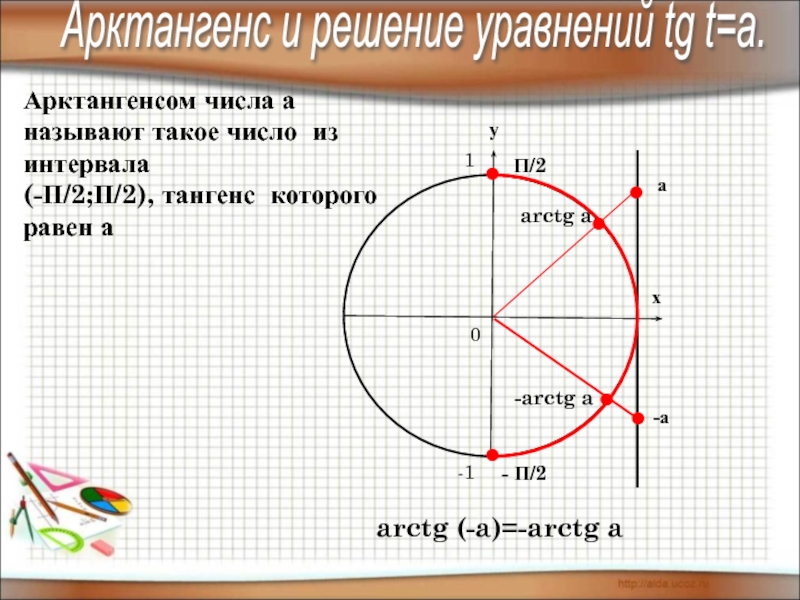
Слайд 13Арктангенсом числа а называют такое число из интервала
(-П/2;П/2), тангенс которого
arctg a
а
П/2
- П/2
arctg (-a)=-arctg a
-а
-arctg a
Арктангенс и решение уравнений tg t=a.
Слайд 14
*
Арктангенс и решение уравнений tg t=a.
Решим при помощи
числовой окружности
уравнение tg t=a.
arctg
а
a – любое число.
Частных случаев нет.
t=arctg a+Пk.
Слайд 15
у
х
0
1
П
0
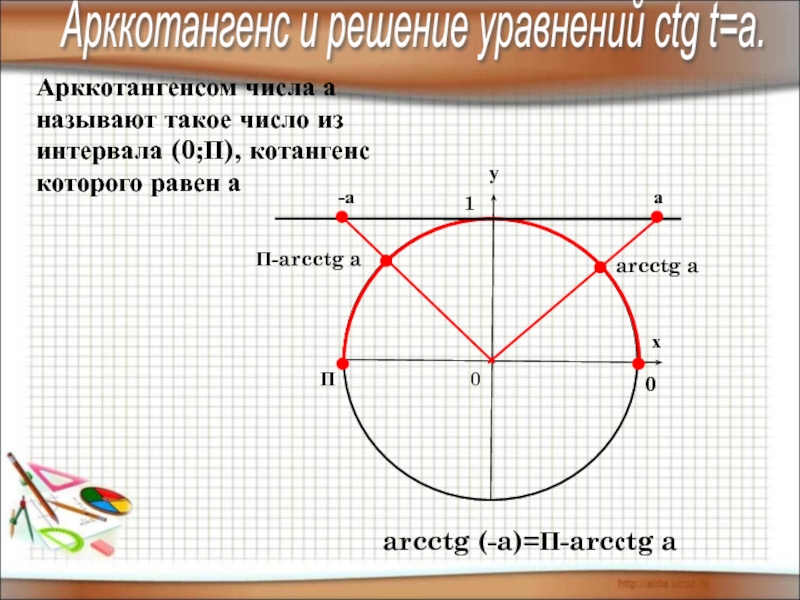
Арккотангенсом числа а называют такое число из интервала (0;П), котангенс которого
-а
arcctg a
arcctg (-a)=П-arcсtg a
а
П-arcctg a
Арккотангенс и решение уравнений сtg t=a.
Слайд 16
*
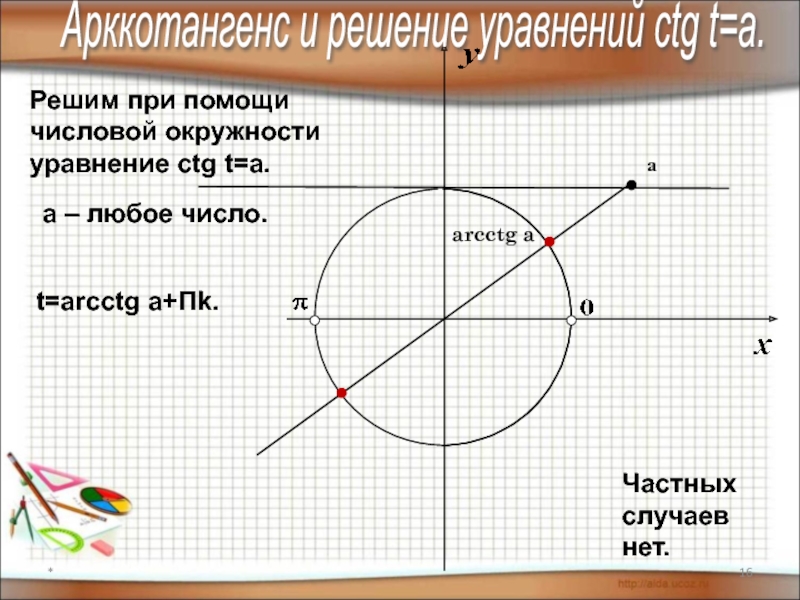
Решим при помощи
числовой окружности
уравнение сtg t=a.
arcctg a
а
a – любое число.
Частных случаев
t=arcctg a+Пk.
Арккотангенс и решение уравнений сtg t=a.
Слайд 18
Примеры уравнений.
Уравнение уже имеет простейший
вид
применить формулы приведения и упростить его.
Это частный вид
уравнения cos t=a
a=0
Разделим обе части на 4.
О:
t
t
Слайд 20
Уравнение переносом слагаемого и делением обеих частей легко сводится к простейшему.
Разделим
О:
t
Примеры уравнений.
Слайд 22О:
Уравнение уже имеет простейший
вид
можно использовать четность функции cos, применить формулы приведения и упростить его.
Примеры уравнений.
Слайд 23О:
Здесь уместно использовать формулу косинуса разности
аргументов:
Теперь уравнение
имеет простейший вид.
Решение
Примеры уравнений.
