- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение обыкновенных дифференциальных уравнений (задача Коши) презентация
Содержание
- 1. Решение обыкновенных дифференциальных уравнений (задача Коши)
- 2. Классификация дифференциальных уравнений обыкновенные дифференциальные уравнения, содержащие
- 3. Примеры дифференциальных уравнений уравнение свободных колебаний
- 4. Типы задач задача Коши краевая задача Чтобы
- 5. Решение ОДУ в MathCAD Given :=Odesolve(,,[])
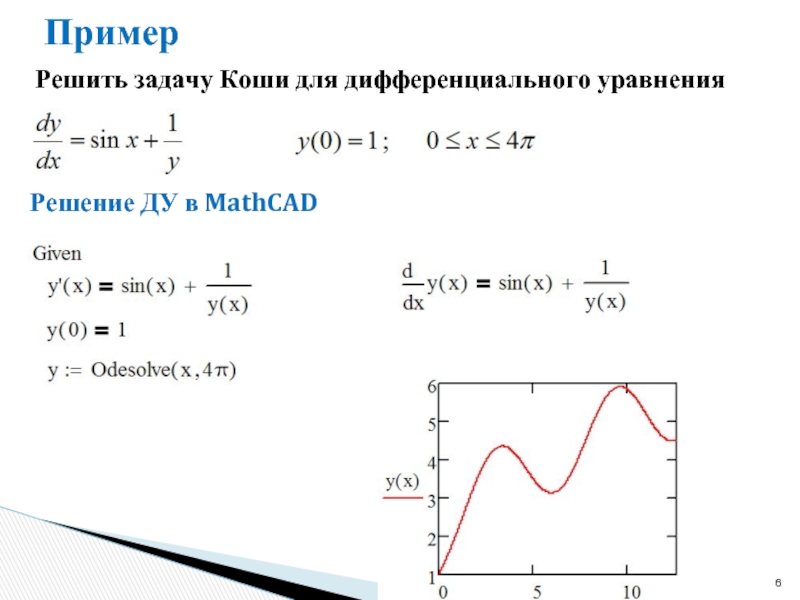
- 6. Пример Решить задачу Коши для дифференциального уравнения Решение ДУ в MathCAD
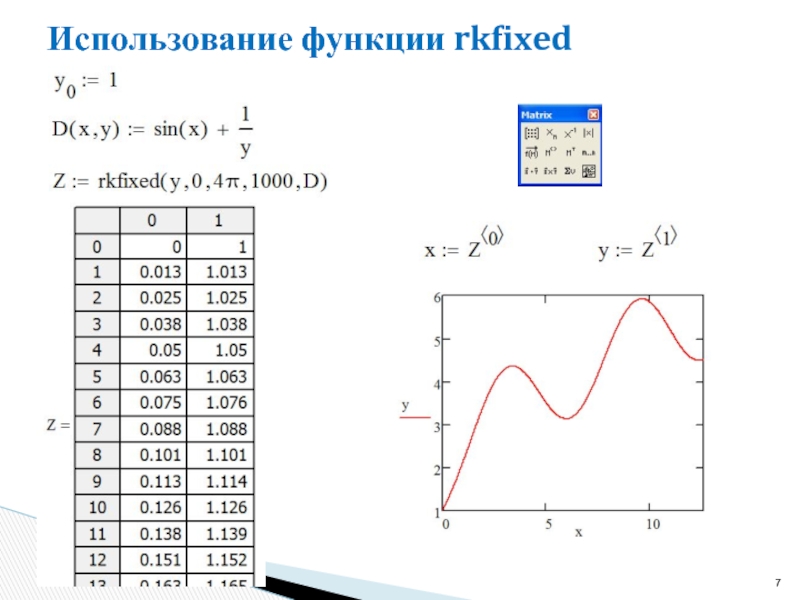
- 7. Использование функции rkfixed
- 8. Численные методы решения задачи Коши Две группы
- 9. Численные методы решения задачи Коши Одношаговые методы:
- 10. Погрешности Источники погрешностей: погрешность округления; погрешность усечения;
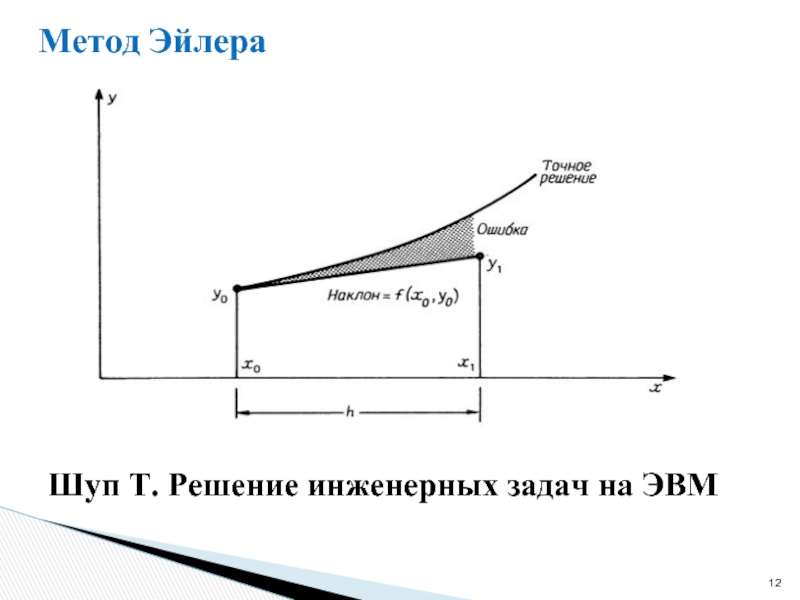
- 11. Метод Эйлера Формула Эйлера рекуррентное соотношение
- 12. Шуп Т. Решение инженерных задач на ЭВМ Метод Эйлера
- 13. Программирование метода Эйлера double f(double x, double
- 14. Программирование метода Эйлера void rdy_Eiler(double *x, double
- 15. Программирование метода Эйлера void __fastcall TForm1::Button1Click(TObject *Sender)
- 16. Модифицированный метод Эйлера Ошибка
- 17. Модифицированный метод Эйлера void rdy_MEiler(double *x, double
- 18. Метод Рунге-Кутты Ошибка
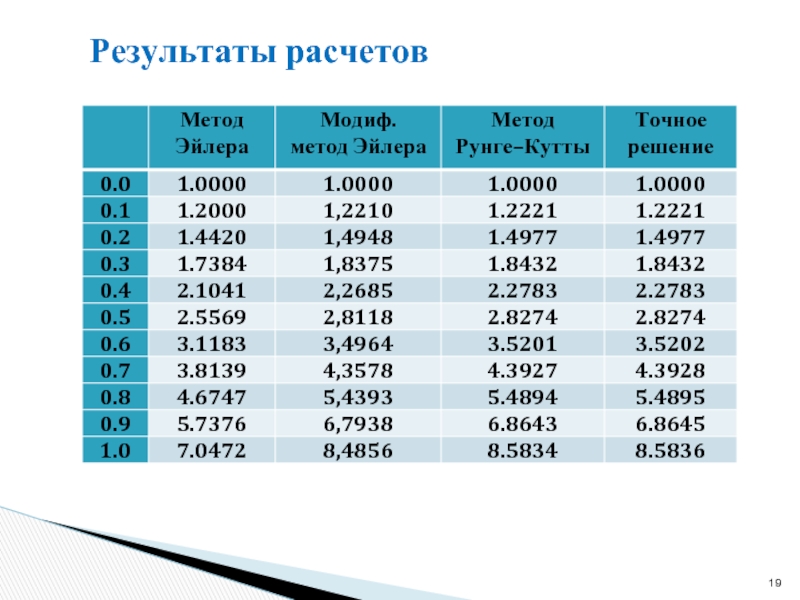
- 19. Результаты расчетов
- 20. Общая характеристика одношаговых методов чтобы получить информацию
- 21. Методы прогноза и коррекции Для этого применяются
- 22. Метод Милна Этап прогноза (формула Милна): Этап
- 23. Метод Милна void rdy_Miln(double *x, double *y,
- 24. Метод Милна while (1)
- 25. Методы Рунге–Кутты для системы дифференциальных уравнений Начальные условия
- 26. Методы Рунге–Кутты для системы дифференциальных уравнений
- 27. Методы Рунге–Кутты для системы дифференциальных уравнений
- 28. Методы Рунге–Кутты для системы дифференциальных уравнений
- 29. Задание Написать программу решения обыкновенного дифференциального уравнения
- 30. Благодарю за внимание!
Слайд 2Классификация дифференциальных уравнений
обыкновенные дифференциальные уравнения, содержащие одну независимую переменную и производные
дифференциальные уравнения в частных производных, содержащие несколько независимых переменных и производные по ним.
В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных:
Слайд 3Примеры дифференциальных уравнений
уравнение
свободных колебаний
уравнение
вынужденных колебаний
уравнение Лапласа
одномерное
волновое уравнение
уравнение
Слайд 4Типы задач
задача Коши
краевая задача
Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения
Задача Коши (задача с начальными условиями) –
дополнительные условия задаются при одном значении независимой переменной
Краевая задача – дополнительные условия задаются при двух или более значениях независимой переменной.
Решение ОДУ
Слайд 8Численные методы решения задачи Коши
Две группы методов:
одношаговые методы;
методы прогноза и коррекции
Слайд 9Численные методы решения задачи Коши
Одношаговые методы:
метод Эйлера;
модифицированный метод Эйлера;
метод Рунге-Кутты.
Методы прогноза
метод Милна;
метод Адамса–Башфорта;
метод Хемминга.
Слайд 10Погрешности
Источники погрешностей:
погрешность округления;
погрешность усечения;
погрешность распространения.
Погрешность распространения – результат накопления погрешностей, появившихся
Указанные три источника погрешностей являются причиной наблюдаемых ошибок двух типов:
локальная ошибка – сумма погрешностей, вносимых в вычислительный процесс на каждом шаге вычислений;
глобальная ошибка – суммарная погрешность, накопившаяся с момента начала вычислений.
Слайд 14Программирование метода Эйлера
void rdy_Eiler(double *x, double *y, double b, int n)
{
double h = (b-x[0])/n;
for (i=0; i
x[i+1] = x[i] + h;
y[i+1] = y[i] + h*f(x[i], y[i]);
}
}
Слайд 15Программирование метода Эйлера
void __fastcall TForm1::Button1Click(TObject *Sender)
{
double *x, *y;
char s[100];
x = new double[n+1];
y = new double[n+1];
x[0] = 0;
y[0] = 1;
rdy_Eiler(x, y, 1, n);
Memo1->Lines->Clear();
for (i=0; i<=n; i++)
{
sprintf(s, "%4.1f %9.4f", x[i], y[i]);
Memo1->Lines->Add(s);
}
delete[] y;
delete[] x;
}
Слайд 17Модифицированный метод Эйлера
void rdy_MEiler(double *x, double *y, double b, int n)
{
double h = (b-x[0])/n, y1;
for (i=0; i
x[i+1] = x[i] + h;
y1 = y[i] + h*f(x[i], y[i]);
y[i+1] = y[i]+0.5*h*(f(x[i], y[i])+f(x[i+1], y1));
}
}
Слайд 20Общая характеристика одношаговых методов
чтобы получить информацию в новой точке, надо иметь
в основе всех одношаговых методов лежит разложение функции в ряд Тейлора;
все одношаговые методы не требуют вычисления производных;
свойство «самостартования» позволяет легко менять величину шага.
Слайд 21Методы прогноза и коррекции
Для этого применяются две формулы:
формула прогноза;
формула коррекции.
В этих
Слайд 22Метод Милна
Этап прогноза (формула Милна):
Этап коррекции (формула Симпсона):
Методы прогноза и коррекции
(в формулах используется информация о нескольких ранее полученных точках).
Перед применением метода прогноза и коррекции необходимо вычислить исходные данные с помощью какого-либо одношагового метода.
Слайд 23Метод Милна
void rdy_Miln(double *x, double *y, double b, int n)
{
int
double h = (b-x[0])/n, y1, dy1, dy2;
double *dy;
dy = new double[n+1];
rdy_RKT(x, y, x[0]+3*h, 3);
for (i=0; i<=3; i++)
dy[i] = f(x[i], y[i]);
for (i=3; i
x[i+1] = x[i] + h;
y1 = y[i-3]+4./3*h*(2*dy[i]-dy[i-1]+2*dy[i-2]);
dy1 = f(x[i+1], y1);
Слайд 24Метод Милна
while (1)
{
y1
dy2 = f(x[i+1], y1);
if (fabs(dy2-dy1)<1e-3) break;
dy1 = dy2;
}
dy[i+1] = dy2;
y[i+1] = y[i-1]+h/3*(dy[i+1]+4*dy[i]+dy[i-1]);
}
delete[] dy;
}
Слайд 29Задание
Написать программу решения обыкновенного дифференциального уравнения с использованием метода Эйлера (Delphi)
Написать программу решения обыкновенного дифференциального уравнения с использованием модифицированного метода Эйлера (Mathcad) с построением графика.
Написать программу решения обыкновенного дифференциального уравнения с использованием модифицированного метода Эйлера (Delphi) с построением графика.
Написать программу решения обыкновенного дифференциального уравнения с использованием модифицированного метода Эйлера (Mathcad) с построением графика.
Написать программу решения обыкновенного дифференциального уравнения с использованием метода Рунге-Кутты (Delphi) с построением графика.
Написать программу решения обыкновенного дифференциального уравнения с использованием метода Рунге-Кутты (Mathcad) с построением графика.




![Решение ОДУ в MathCADGiven :=Odesolve(,,[])](/img/tmb/3/244393/378a87a8ecb5b67bd92743aece153ce2-800x.jpg)














![Метод Милна while (1) { y1 = y[i-1] + h/3*(dy1 + 4*dy[i] + dy[i-1]);](/img/tmb/3/244393/ea70b5737b4b841b0420a464d2ba2d68-800x.jpg)