- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение нелинейных уравнений презентация
Содержание
- 1. Решение нелинейных уравнений
- 2. РЕШЕНИЕ УРАВНЕНИЙ Решить уравнение – значит найти
- 3. КЛАССЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В зависимости от
- 4. КЛАССЫ НЕЛИНЕЙНЫХ ФУНКЦИЙ
- 5. АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ Алгебраическая функция –
- 6. Пример рациональной алгебраической функции Рациональная алгебраическая функция:
- 7. ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ Целая рациональная алгебраическая функция: Иррациональная алгебраическая функция:
- 8. АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ Дробно-рациональная алгебраическая функция:
- 9. ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ Трансцендентные функции – все неалгебраические
- 10. ЭТАПЫ НАХОЖДЕНИЙ КОРНЯ Процесс нахождения приближенных значений
- 11. ЛОКАЛИЗАЦИЯ КОРНЕЙ Отделить корни – это значит
- 12. СПОСОБЫ ОТДЕЛЕНИЯ КОРНЕЙ Отделение корней можно произвести двумя методами: графическим, аналитическим.
- 13. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ I способ: Средствами
- 14. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ II способ: Все
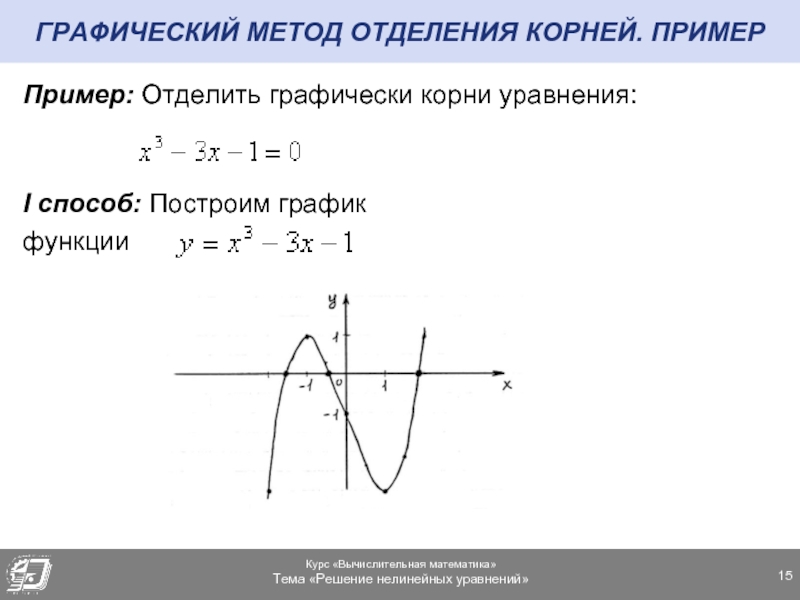
- 15. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР Пример: Отделить
- 16. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР II способ:
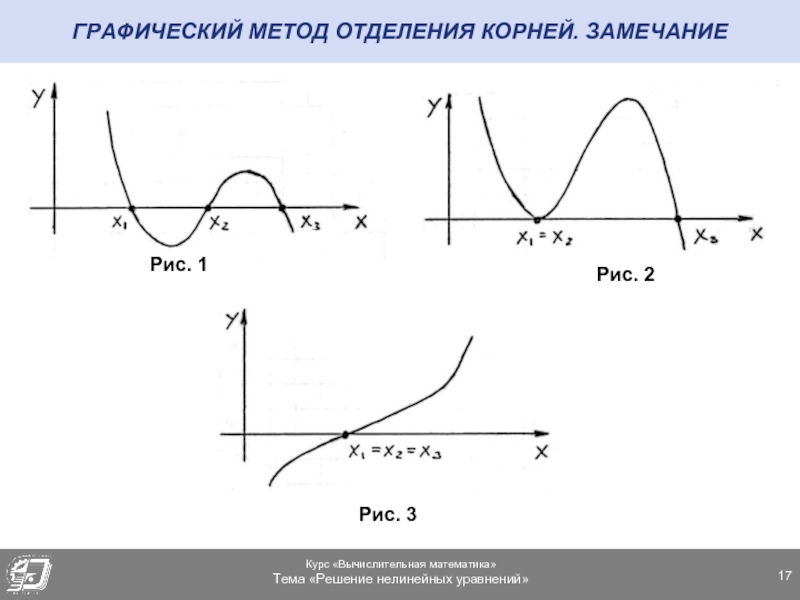
- 17. ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ЗАМЕЧАНИЕ Рис. 1 Рис. 2 Рис. 3
- 18. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Аналитически корни уравнения
- 19. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Теорема 2.
- 20. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Теорема 3.
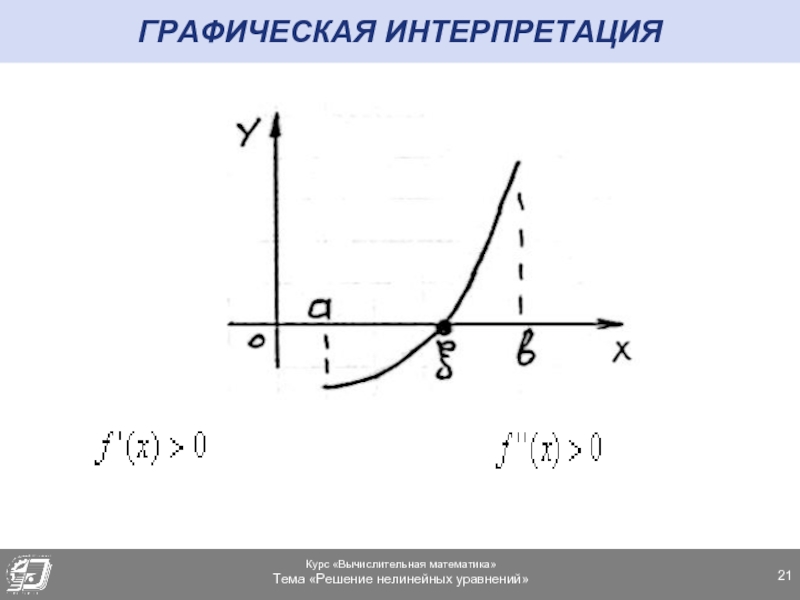
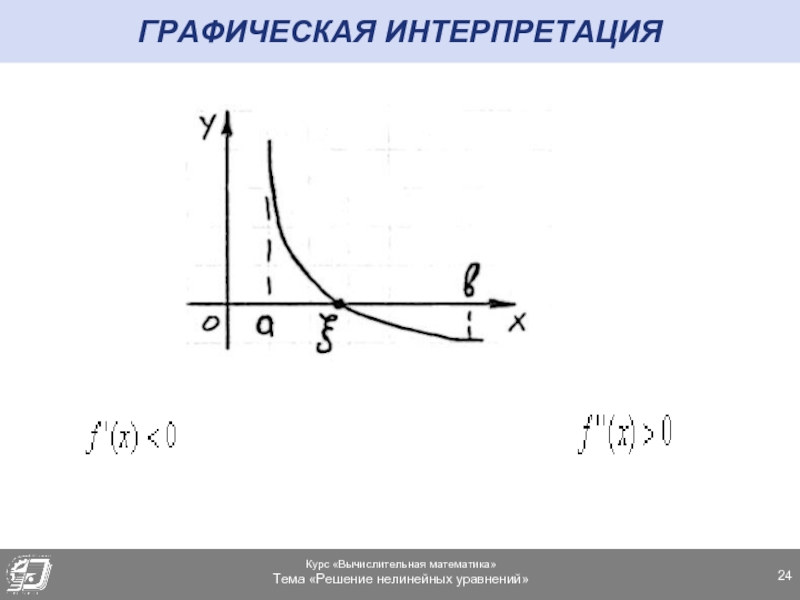
- 21. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
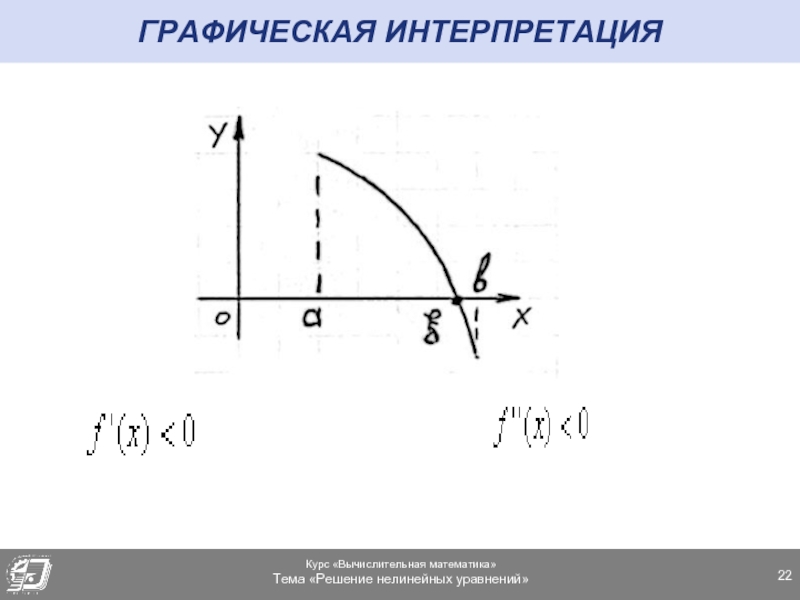
- 22. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
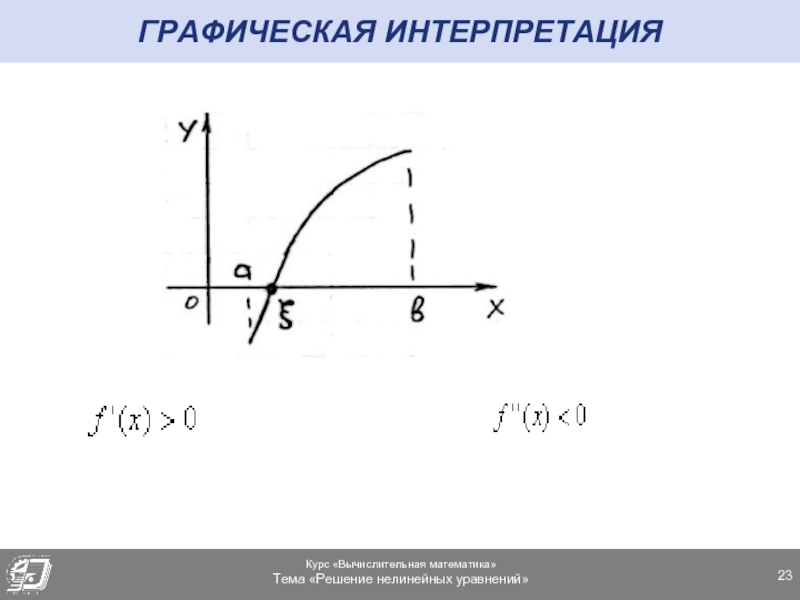
- 23. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
- 24. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
- 25. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ Для того чтобы
- 26. ПОРЯДОК ДЕЙСТВИЙ ДЛЯ ОТДЕЛЕНИЯ КОРНЕЙ АНАЛИТИЧЕСКИМ
- 27. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
- 28. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР Составим таблицу
- 29. АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР Уравнение имеет
- 30. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 1: (о
- 31. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Следствие: Алгебраическое уравнение
- 32. КРАТНОСТЬ КОРНЯ Число x есть корень
- 33. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
- 34. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 3: (теорема
- 35. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 4: (о
- 36. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Тогда положительные корни
- 37. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 5: (теорема
- 38. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Число S2 отрицательных
- 39. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ Теорема 6: (теорема
- 40. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР Согласно
- 41. ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР
- 42. ЛОКАЛИЗАЦИЯ ПОЛОЖИТЕЛЬНЫХ КОРНЕЙ
- 43. ЛОКАЛИЗАЦИЯ ПОЛОЖИТЕЛЬНЫХ КОРНЕЙ
- 44. ЛОКАЛИЗАЦИЯ ОТРИЦАТЕЛЬНЫХ КОРНЕЙ Рассчитаем границы отрицательных корней по Теоремам 3 и 4:
- 45. ЛОКАЛИЗАЦИЯ ОТРИЦАТЕЛЬНЫХ КОРНЕЙ
- 46. Нахождение числа положительных корней уравнения Определим количество
- 47. Нахождение числа отрицательных корней уравнения Определим количество
- 48. Исследование структуры корней По Теореме Гюа исследуем
- 49. Уточнение корней Уточнение корней – это доведение
- 50. УТОЧНЕНИЕ КОРНЕЙ Пусть дано уравнение f(x)=0,
- 51. МЕТОДЫ УТОЧНЕНИЯ КОРНЕЙ 1. МЕТОДЫ ДИХОТОМИИ
- 52. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ Возьмем на отрезке [a,b]
- 53. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ (2) (1)
- 54. Априорная оценка метода половинного деления Априорная
- 55. МЕТОД ХОРД Пробная точка c находится как
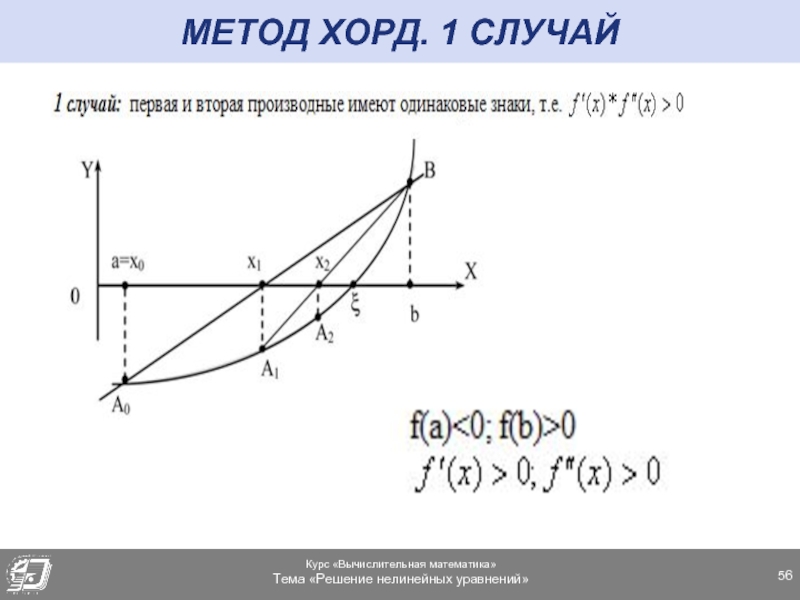
- 56. МЕТОД ХОРД. 1 СЛУЧАЙ
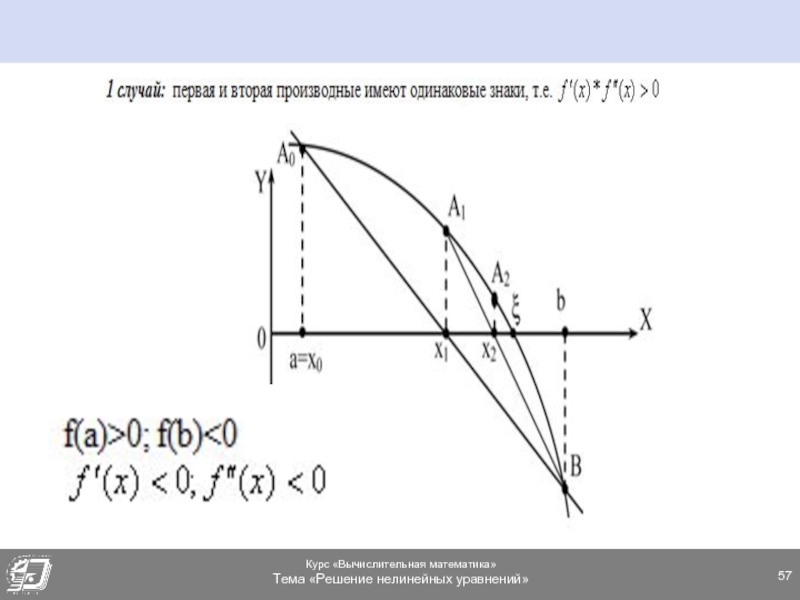
- 58. МЕТОД ХОРД. 1 СЛУЧАЙ
- 59. МЕТОД ХОРД. 1 СЛУЧАЙ (2)
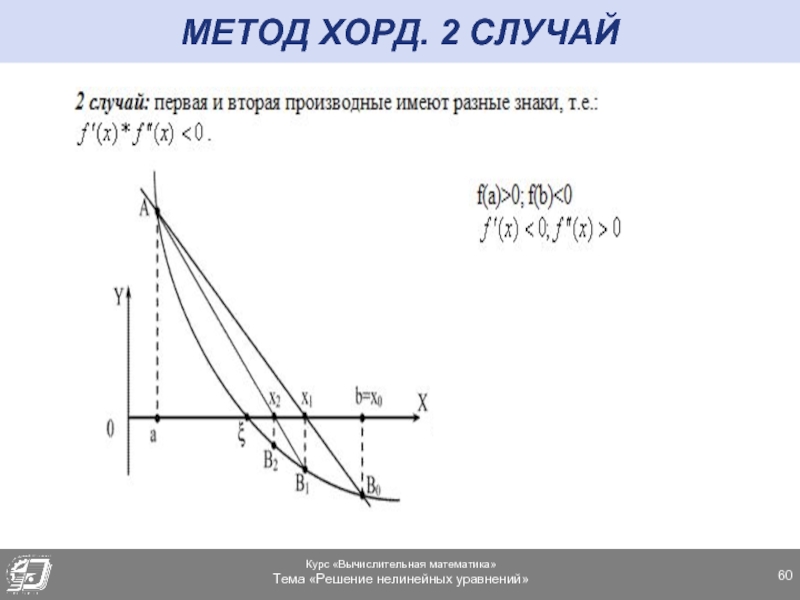
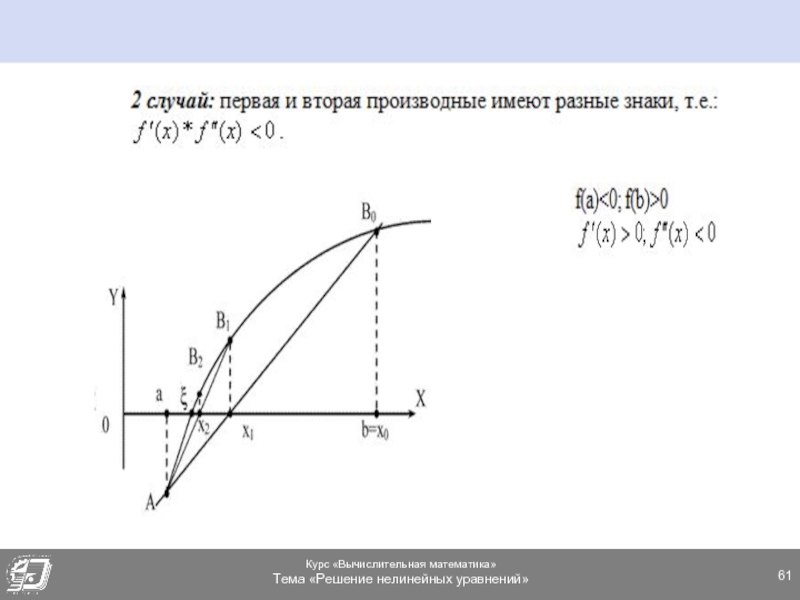
- 60. МЕТОД ХОРД. 2 СЛУЧАЙ
- 62. МЕТОД ХОРД. 2 СЛУЧАЙ
- 63. МЕТОД ХОРД. 2 СЛУЧАЙ В общем случае: (3)
- 64. Выбор формулы (2) или (3) можно
- 65. МЕТОД ХОРД
- 66. МЕТОД ХОРД. УСЛОВИЕ ОСТАНОВА ПРОЦЕССА
- 67. МЕТОД ХОРД. УСЛОВИЕ ОСТАНОВА ПРОЦЕССА
- 68. МЕТОД ХОРД. ПРИМЕР
- 69. МЕТОД ХОРД. ПРИМЕР
- 70. МЕТОД ХОРД. ПРИМЕР
- 71. МЕТОД ХОРД. ПРИМЕР
- 72. МЕТОД ХОРД. ПРИМЕР
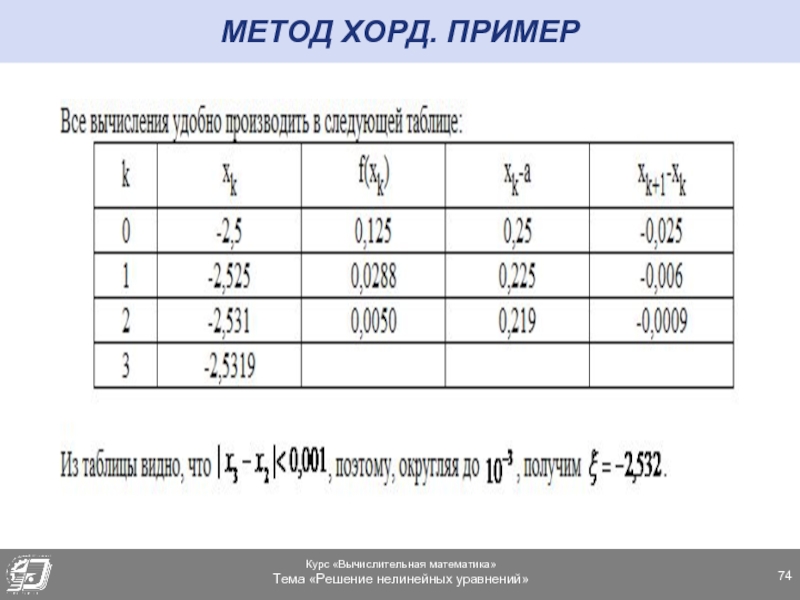
- 73. МЕТОД ХОРД. ПРИМЕР
- 74. МЕТОД ХОРД. ПРИМЕР
- 75. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ Дано
- 76. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
- 77. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ [a, b]⊃ [a1, b1]⊃ [a2, b2]⊃… [ak, bk ]⊃… Возрастающая функция
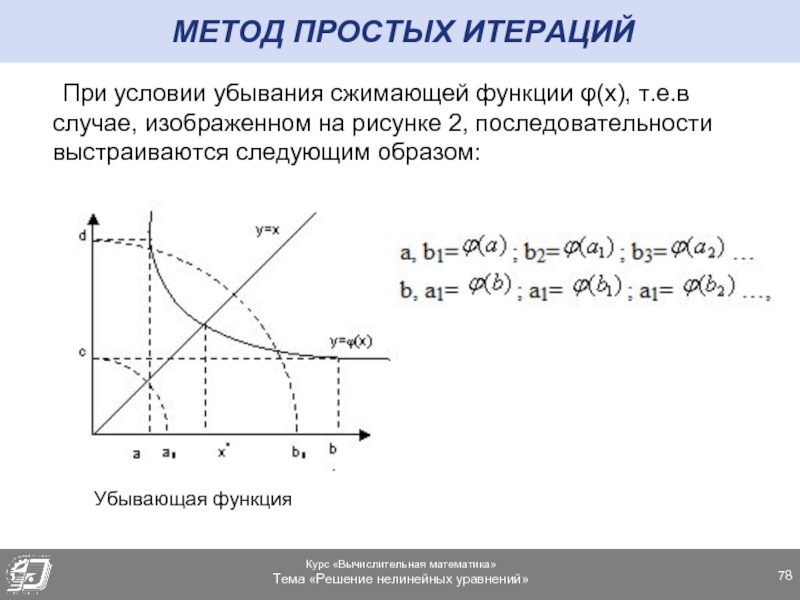
- 78. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ При условии убывания
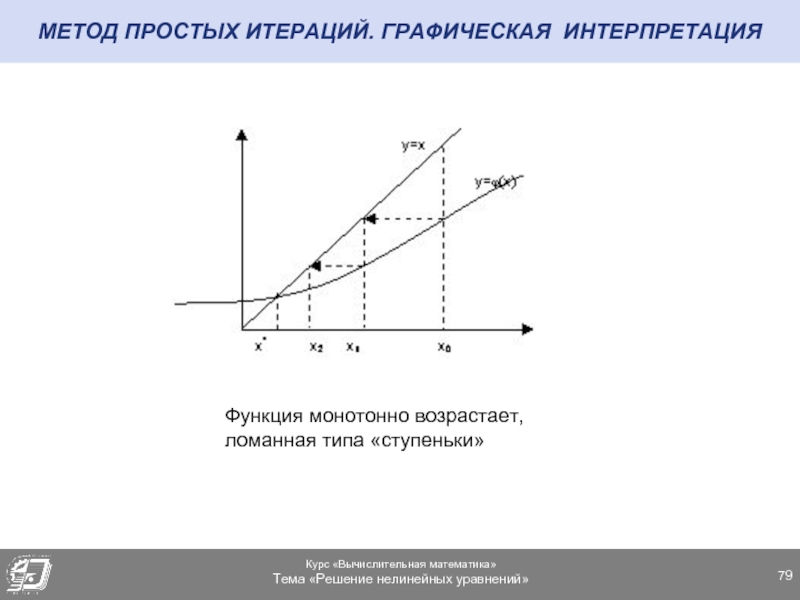
- 79. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ Функция монотонно возрастает, ломанная типа «ступеньки»
- 80. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ Функция монотонно убывает, ломанная типа «спираль»
- 81. МЕТОД ПРОСТЫХ ИТЕРАЦИЙ Выводы: На некотором промежутке
- 82. УСЛОВИЯ СХОДИМОСТИ ИТЕРАЦИОННОГО ПРОЦЕССА
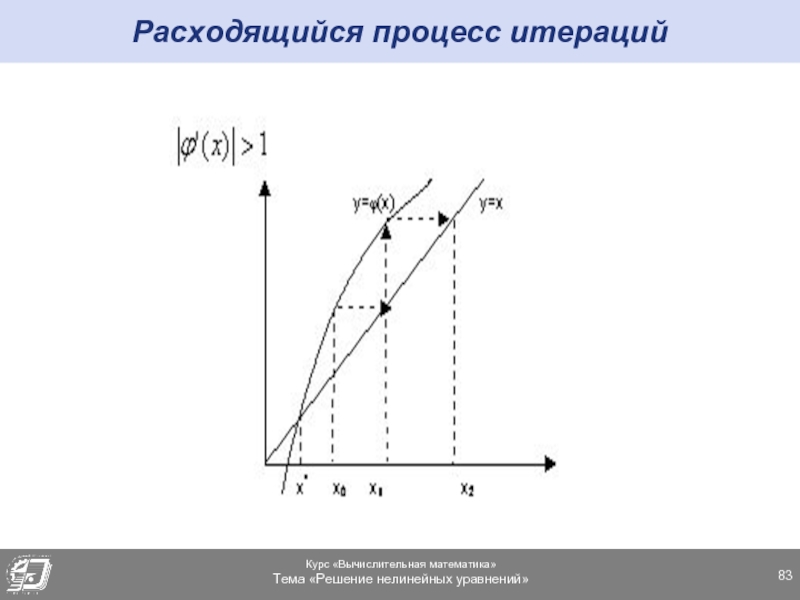
- 83. Расходящийся процесс итераций
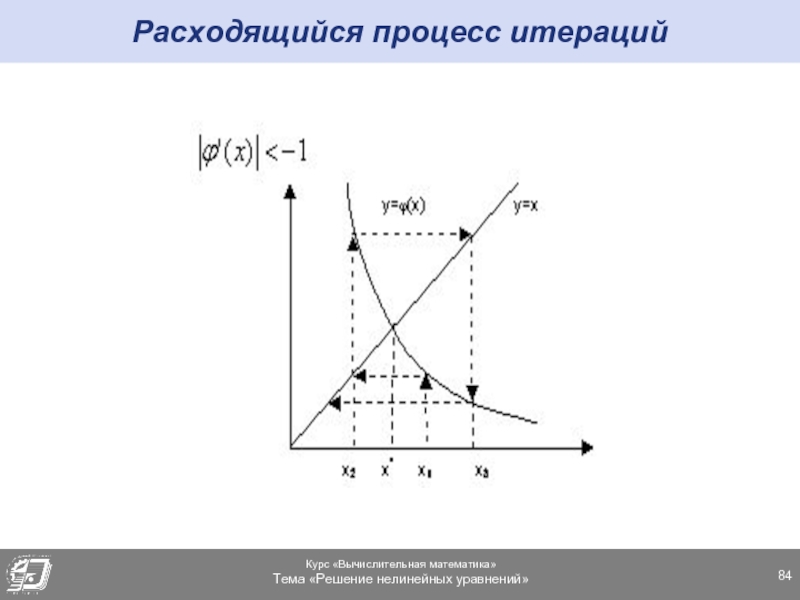
- 84. Расходящийся процесс итераций
- 85. АПОСТЕРИОРНАЯ ОЦЕНКА Используется для остановки итерационного процесса
- 86. Априорная оценка Используется для предварительного расчета количества операций
- 87. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
- 88. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
- 89. СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2) Выражаем x из : f(x)=0 x=φ(x);
- 90. ПРИМЕР
- 91. ПРИМЕР
- 92. ПРИМЕР
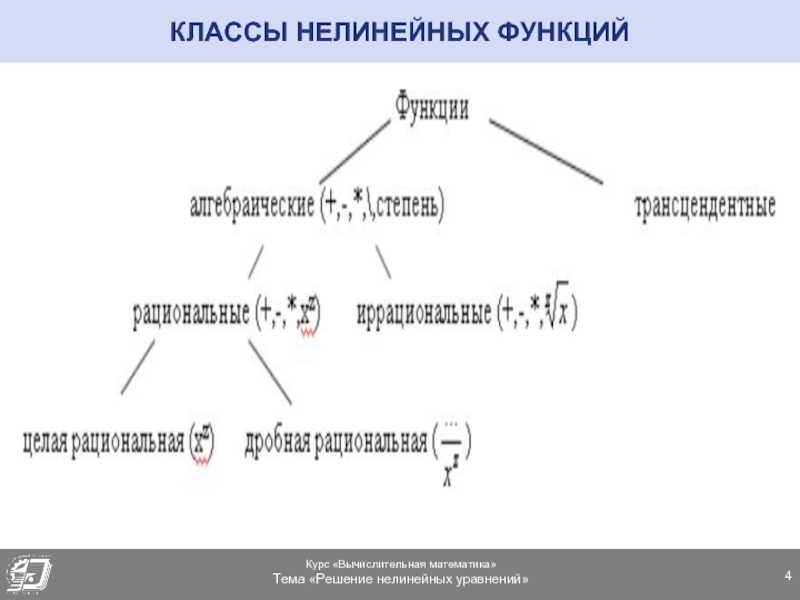
- 93. ПРИМЕР
- 94. © ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова,
Слайд 1Тема «Решение нелинейных уравнений»
Ижевск
2013
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Автор Исенбаева Е.Н., старший преподаватель
Слайд 2РЕШЕНИЕ УРАВНЕНИЙ
Решить уравнение – значит найти
множество всех корней этого
уравнения.
При
корни вычислены с заданной степенью сложности-> задача нахождения корней считается решенной.
Слайд 3КЛАССЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
В зависимости от того, какие функции входят в уравнение
алгебраические,
трансцендентные.
Слайд 5АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ
Алгебраическая функция – функция,
содержащая арифметические операции
(+, -, *,
показателем.
Слайд 7ПРИМЕРЫ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
Целая рациональная алгебраическая функция:
Иррациональная алгебраическая функция:
Слайд 9ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
Трансцендентные функции – все неалгебраические функции: показательная ax , логарифмическая
Слайд 10ЭТАПЫ НАХОЖДЕНИЙ КОРНЯ
Процесс нахождения приближенных значений корней уравнения разбивается на 2
1) отделение корней,
2) уточнение корней до заданной степени точности.
Слайд 11ЛОКАЛИЗАЦИЯ КОРНЕЙ
Отделить корни – это значит разбить всю область допустимых значений
Корень уравнения f(x)=0 считается отделенным на [a, b], если на этом отрезке уравнение f(x)=0 не имеет других корней.
Слайд 12СПОСОБЫ ОТДЕЛЕНИЯ КОРНЕЙ
Отделение корней можно произвести двумя методами:
графическим,
аналитическим.
Слайд 13ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ
I способ: Средствами машинной графики функция f(x) представляется
Слайд 14ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ
II способ: Все члены уравнения f(x)=0 разбивают на
Слайд 15ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
Пример: Отделить графически корни уравнения:
I способ:
функции
Слайд 16ГРАФИЧЕСКИЙ МЕТОД ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
II способ: Представим данное уравнение в виде
и
Слайд 18АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Аналитически корни уравнения f(x)=0 можно отделить, используя некоторые
Теорема 1. Если функция f(x) непрерывна на отрезке [a, b] и принимает на концах
этого отрезка значения разных знаков, то внутри отрезка [a, b] существует, по крайней мере, один корень уравнения f(x)=0 .
Слайд 19АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Теорема 2. Если функция f(x) непрерывна и монотонна
Слайд 20АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Теорема 3. Если функция f(x) непрерывна на отрезке
Слайд 25АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ
Для того чтобы определить наибольшее и наименьшее значение
1) Определить критические точки функции, т.е. точки, в которых первая производная функции равна нулю или не существует, но функция сохраняет непрерывность.
2) Вычислить значения функции в критических точках и на концах отрезка [a, b].
3) Наибольшее из значений, найденных в п.2, будет наибольшим, а наименьшее – наименьшим значением функции на отрезке.
Слайд 26ПОРЯДОК ДЕЙСТВИЙ ДЛЯ ОТДЕЛЕНИЯ КОРНЕЙ
АНАЛИТИЧЕСКИМ МЕТОДОМ
1) Находят f’(x).
2) Составляют таблицу
а) критическим значениям (корням) производной или ближайшим к ним
б) граничным значениям (исходя из ОДЗ неизвестного).
3) Определяют интервалы, на концах которых функция принимает значения противоположных знаков. Внутри этих интервалов содержится по одному и только по одному корню.
Слайд 28АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
Составим таблицу знаков функции f(x), полагая х
а) критическим значениям (корням производной) или ближайшим к ним;
б) граничным значениям
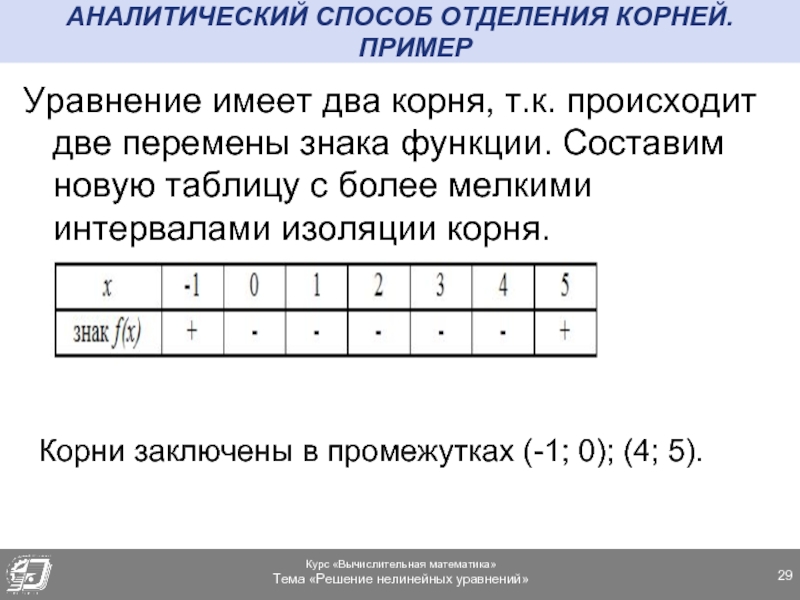
Слайд 29АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙ. ПРИМЕР
Уравнение имеет два корня, т.к. происходит две
Корни заключены в промежутках (-1; 0); (4; 5).
Слайд 30ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 1: (о числе корней алгебраического уравнения
действительные числа (1)
Алгебраическое уравнение n-й степени имеет ровно n корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.
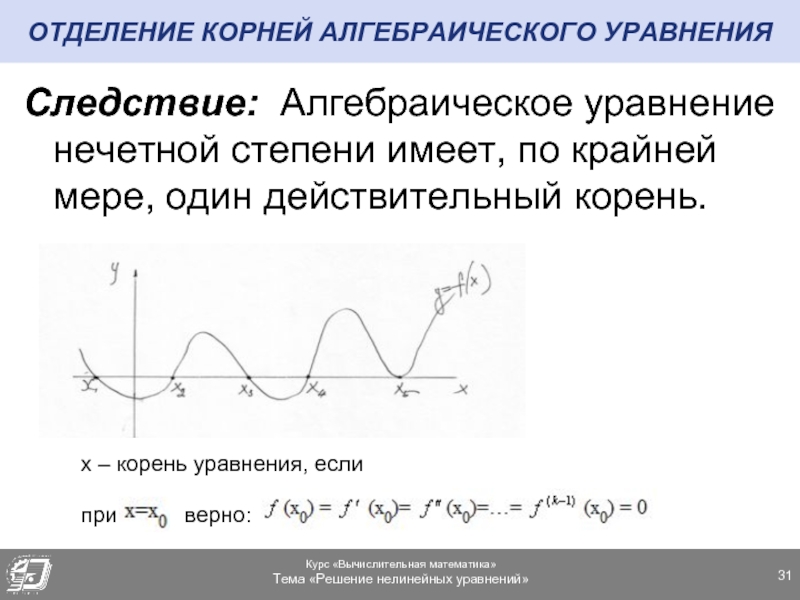
Слайд 31ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Следствие: Алгебраическое уравнение нечетной степени имеет, по крайней
х – корень уравнения, если
при верно:
Слайд 32КРАТНОСТЬ КОРНЯ
Число x есть корень уравнения (1) кратности k, если при
Простой корень- корень кратности k=1.
Слайд 34ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 3: (теорема Лагранжа о верхней границе
положительных корней
Пусть an > 0 и ai – первый отрицательный
коэффициент в последовательности
C – наибольшая из абсолютных величин отрицательных коэффициентов. Тогда за верхнюю границу положительных корней уравнения принимают число:
Слайд 35ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 4: (о нижних и верхних границах положительных
Слайд 36ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Тогда положительные корни
и отрицательные корни
Слайд 37ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 5: (теорема Декарта о количестве действительных корней
Число S1 положительных корней (с учетом их кратности) алгебраического уравнения
равно числу перемен знаков в последовательности коэффициентов
(коэффициенты = 0 не учитываются) многочлена или меньше этого числа на четное число.
Слайд 38ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Число S2 отрицательных корней (с учетом их кратности)
равно числу перемен знаков в
последовательности коэффициентов
многочлена или меньше этого числа на четное число.
Слайд 39ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ
Теорема 6: (теорема Гюа о необходимом условии действительности
Если алгебраическое уравнение имеет все действительные корни, то квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов.
Слайд 40ОТДЕЛЕНИЕ КОРНЕЙ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ. ПРИМЕР
Согласно Следствию Теоремы 1 уравнение имеет 3
Слайд 46Нахождение числа положительных корней уравнения
Определим количество положительных корней по Теореме 5
=
Коэффициенты многочлена: 1,-1,-9, 9.
Количество перемен знака- 2→ количество
положительных корней уравнения- два
или их нет.
Слайд 47Нахождение числа отрицательных корней уравнения
Определим количество отрицательных корней уравнения. Для уравнения
выпишем
Количество перемен знака- 1 → число
отрицательных корней- один.
Слайд 48Исследование структуры корней
По Теореме Гюа исследуем структуру корней по коэффициентам уравнения:
Необходимое
Слайд 49Уточнение корней
Уточнение корней – это доведение отделенных корней до заданной степени
Второй этап решения алгебраических и трансцендентных уравнений.
Слайд 50УТОЧНЕНИЕ КОРНЕЙ
Пусть дано уравнение f(x)=0, где f(x) – непрерывная функция. Требуется
Будем считать, что корень отделен и находится на отрезке [a,b], т.е. f(a)*f(b)<0, причем |b-a|> .
Здесь f(x) – непрерывная функция.
Слайд 51МЕТОДЫ УТОЧНЕНИЯ КОРНЕЙ
1. МЕТОДЫ ДИХОТОМИИ
-Метод половинного деления
-Метод хорд
2. Метод простых итераций
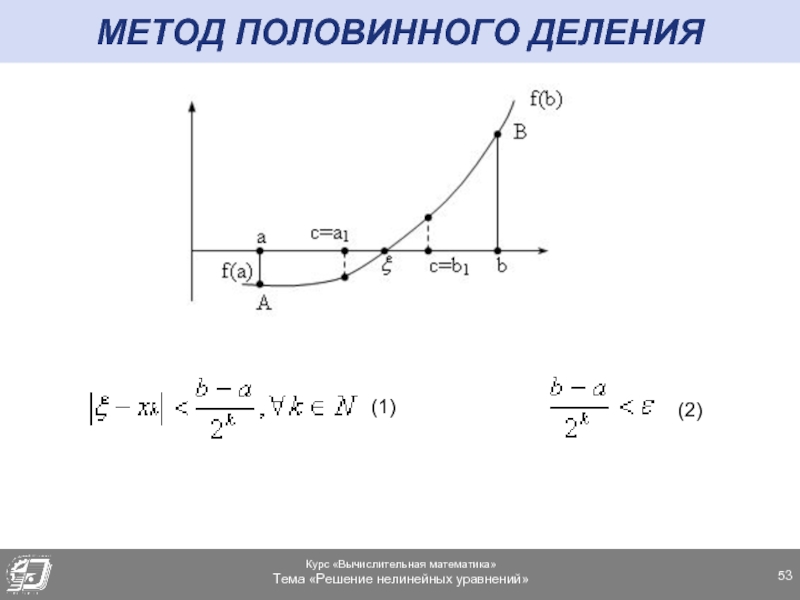
Слайд 52МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Возьмем на отрезке [a,b] промежуточную точку так, чтобы она
Алгоритм метода
1. Задать концы отрезка [a,b], функцию f, малое число >0, вычислить (или ввести) f(a).
2. Вычислить c=(a+b)/2.
3. Если (b-a)<2, то положить c и останов
4. Вычислить f(c)
5. Если f(a)*f(c)<0, положить b=c и вернуться к шагу 2, иначе a=c, f(a)=f(c) и вернуться к шагу 2.
Слайд 54Априорная оценка метода половинного деления
Априорная оценка позволяет предварительно рассчитать примерное
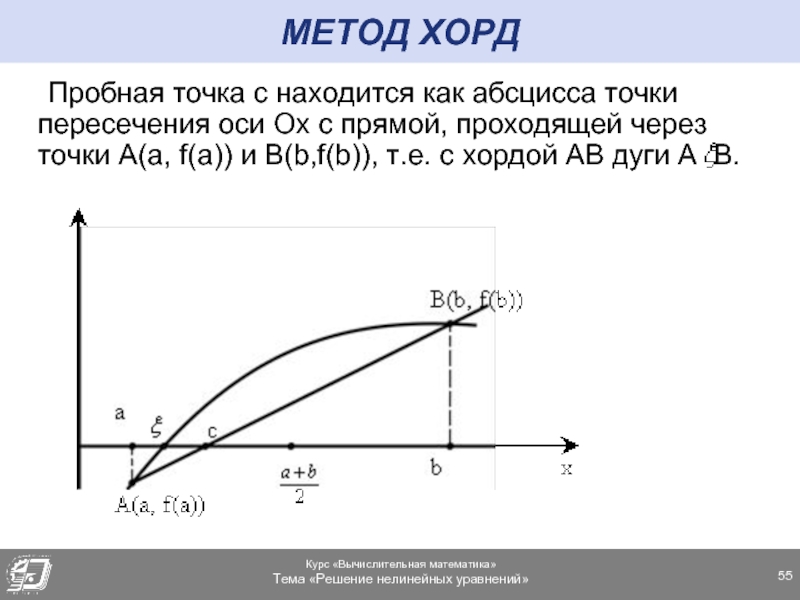
Слайд 55МЕТОД ХОРД
Пробная точка c находится как абсцисса точки пересечения оси Ox
Слайд 64
Выбор формулы (2) или (3) можно осуществить, пользуясь простым правилом: неподвижным
МЕТОД ХОРД
Слайд 65МЕТОД ХОРД
в качестве начального приближения- конец a. При этом используется расчетная формула (2).
→ неподвижен конец a,
в качестве начального приближения-
конец b. При этом используется расчетная формула (3).
Слайд 75МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
Дано (1) (2)
Если
Существование и единственность корня уравнения основывается на принципе сжимающих отображений (принципе неподвижной точки).
Слайд 78 МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
При условии убывания сжимающей функции φ(x), т.е.в случае,
Убывающая функция
Слайд 79МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Функция монотонно возрастает,
ломанная типа «ступеньки»
Слайд 80МЕТОД ПРОСТЫХ ИТЕРАЦИЙ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Функция монотонно убывает,
ломанная типа «спираль»
Слайд 81МЕТОД ПРОСТЫХ ИТЕРАЦИЙ
Выводы:
На некотором промежутке [a,b] функция φ(x) удовлетворяет условиям сжатия,
уравнение x= φ(x) имеет и притом единственный корень x*є[a,b] ;
к этому корню со скоростью геометрической прогрессии сходится определяемая МПИ последовательности (xk), начинающая с
x0є[a,b], причем скорость сходимости тем выше, чем меньше коэффициент сжатия qє(0,1);
3. функция φ(x) монотонно возрастает на [a, b] → приближения xk к x0 также будут монотонными;
4. φ(x) убывает → процесс порождает двустороннее приближение к корню x*.
Слайд 87СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
Заменяем f(x)=0 на равносильное x=x+cf(x),
φ(x)=x
Находим с є [a,b]
Слайд 88СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)
2. Заменяем f(x)=0 на равносильное
Знак
Слайд 94© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна,
СПАСИБО ЗА ВНИМАНИЕ














![АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙТеорема 2. Если функция f(x) непрерывна и монотонна на отрезке [a, b]](/img/tmb/2/126301/7600f25a86b64b1c7c5a70f95f5e89b4-800x.jpg)
![АНАЛИТИЧЕСКИЙ СПОСОБ ОТДЕЛЕНИЯ КОРНЕЙТеорема 3. Если функция f(x) непрерывна на отрезке [a, b] и принимает](/img/tmb/2/126301/b90c69e11445743c78a3d2c44fcd09e6-800x.jpg)

























![МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ Возьмем на отрезке [a,b] промежуточную точку так, чтобы она являлась серединой отрезка [a,b],](/img/tmb/2/126301/def902add07966bc2c5ef5bb532be880-800x.jpg)

















![МЕТОД ПРОСТЫХ ИТЕРАЦИЙ[a, b]⊃ [a1, b1]⊃ [a2, b2]⊃… [ak, bk ]⊃…Возрастающая функция](/img/tmb/2/126301/2b21840f2400160c2df752c7baaa4c84-800x.jpg)

![МЕТОД ПРОСТЫХ ИТЕРАЦИЙВыводы: На некотором промежутке [a,b] функция φ(x) удовлетворяет условиям сжатия, зафиксированным в определении →](/img/tmb/2/126301/04fd27b945217184acd3d5e155a5c943-800x.jpg)



![СПОСОБЫ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ (1) К ВИДУ (2)Заменяем f(x)=0 на равносильное x=x+cf(x), c=const≠0 φ(x)=x Находим с є [a,b]](/img/tmb/2/126301/bfcafbb65f168a2085d37e7c23111656-800x.jpg)