m×2
Приведение антагонистической игры к паре взаимно двойственных задач линейного программирования
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение игр в смешанных стратегиях презентация
Содержание
- 1. Решение игр в смешанных стратегиях
- 2. Введение Сложная стратегия, состоящая в случайном применении
- 3. 1. Геометрическое решение игр 2×2, 2×n, m×2
- 4. Графический метод решения игры 1.1. Геометрическое решение
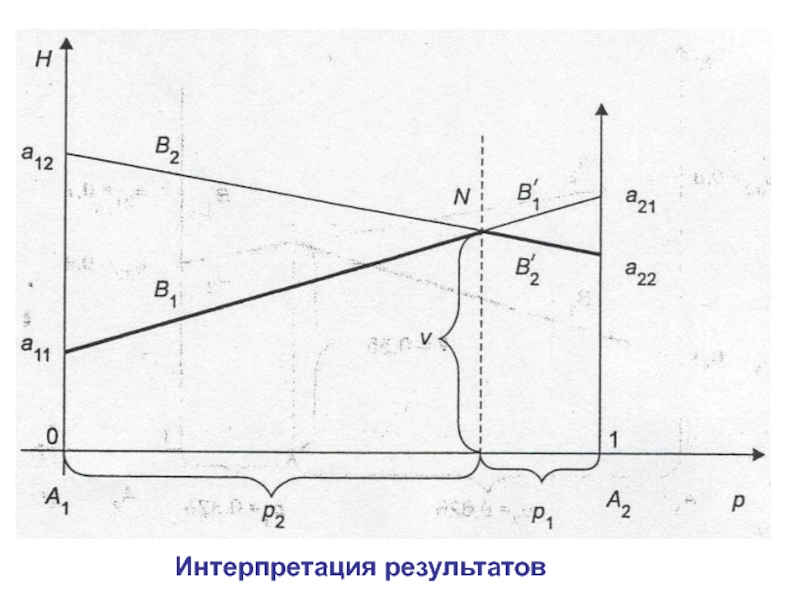
- 5. Интерпретация результатов
- 6. Для уточнения и проверки результатов графического решения
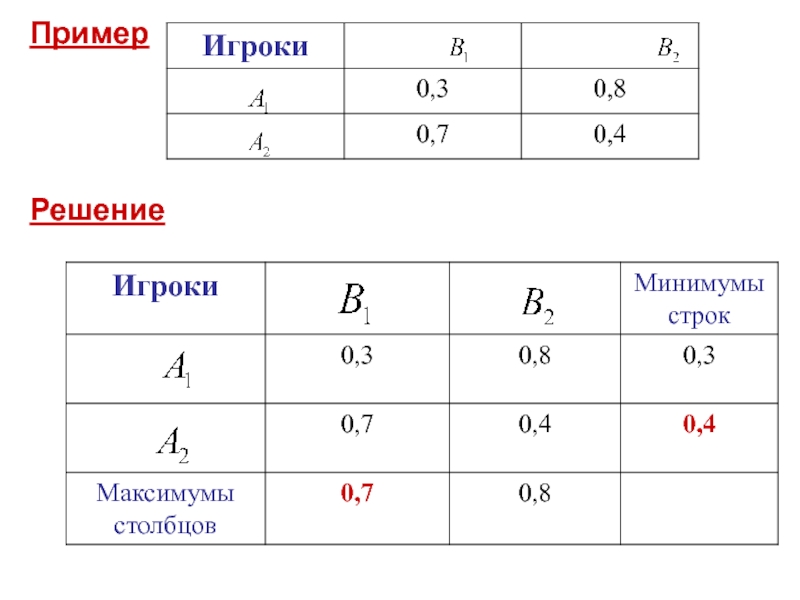
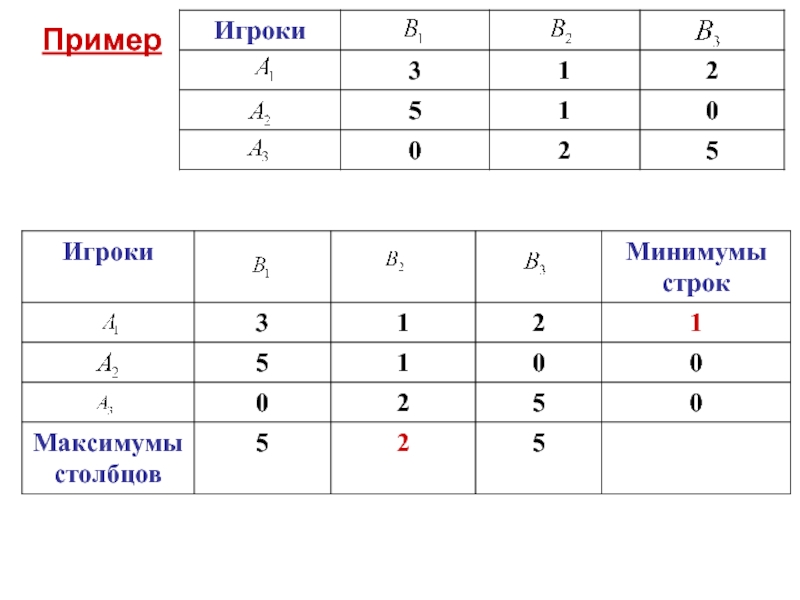
- 7. Пример Решение
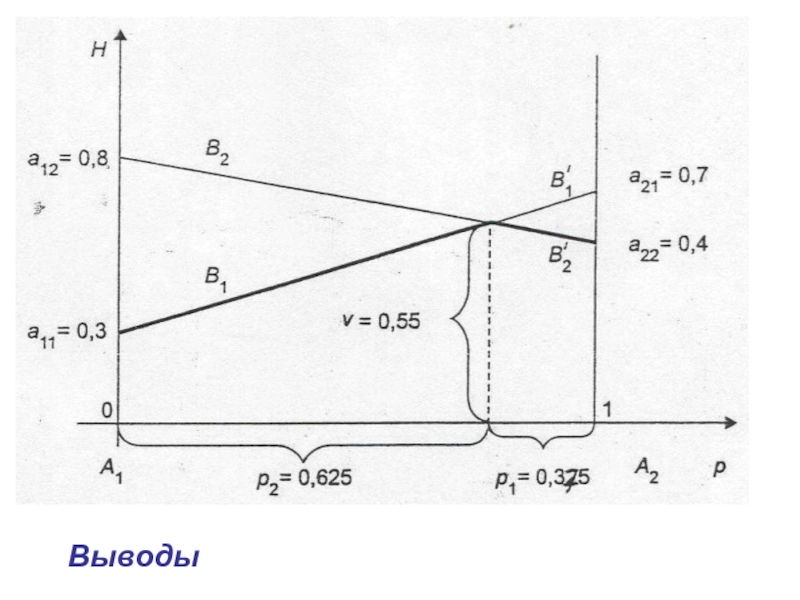
- 8. Выводы
- 9. 1.2. Геометрическое решение игры 2×n
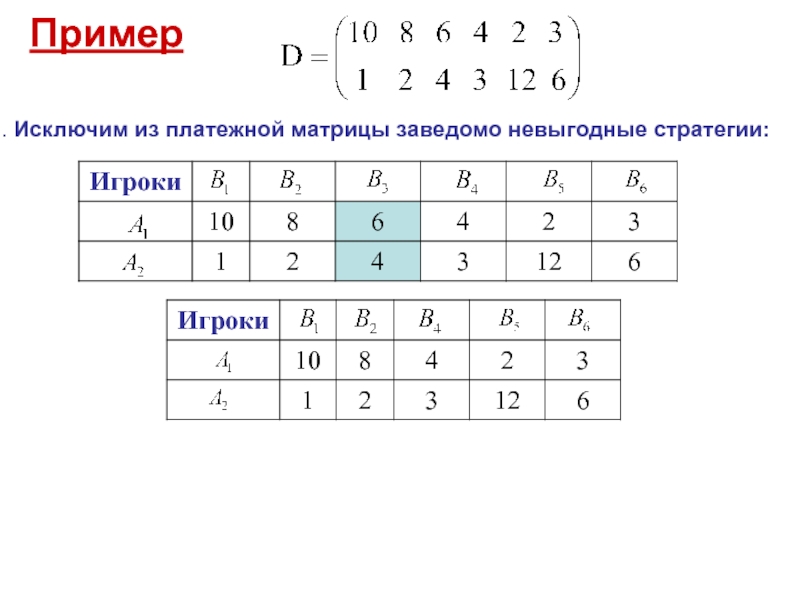
- 10. Пример Исключим из платежной
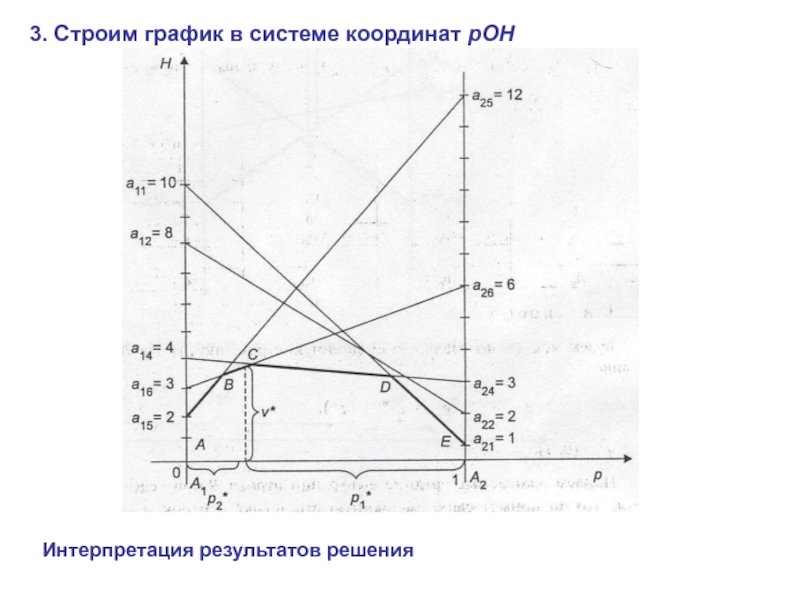
- 12. 3. Строим график в системе координат pOH Интерпретация результатов решения
- 13. 4. Определим значения вероятностей и
- 14. 1.3. Геометрическое решение игры m×2 Необходимо найти смешанные стратегии игроков:
- 16. Пример. Задача о выборе минеральных удобрений Матрица
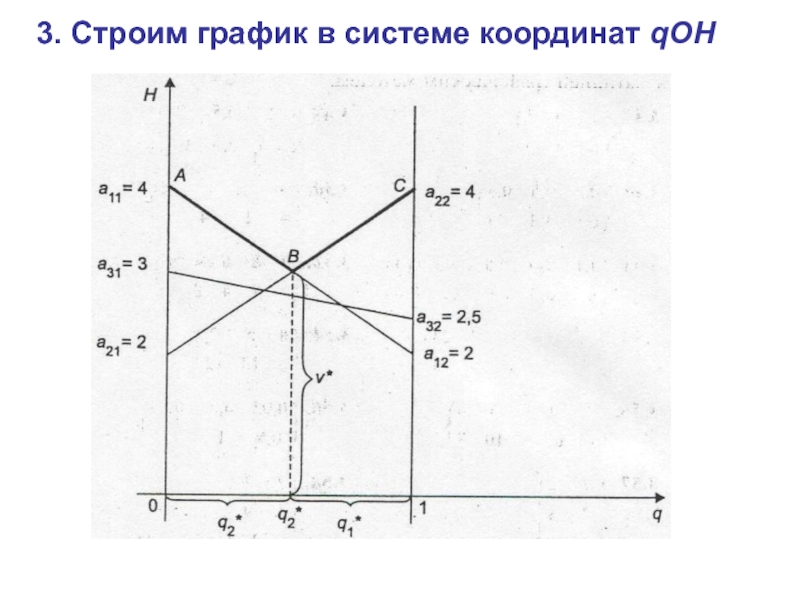
- 17. 3. Строим график в системе координат qOH
- 18. 4. Определим значения вероятностей и
- 19. Общая схема решения игр 2×n и
- 20. 2. Приведение антагонистической игры к паре
- 21. Задача игрока А Задача игрока В
- 22. Пример
- 23. Задача игрока А Задача игрока В
- 24. При решении произвольной конечной игры размера
Введение Сложная стратегия, состоящая в случайном применении двух и более чистых стратегий с определенными частотами, называется смешанной Основная теорема теории игр Дж. фон Неймана Наборы вероятностей (частот)
Слайд 2Введение
Сложная стратегия, состоящая в случайном применении двух и более чистых стратегий
с определенными частотами, называется смешанной
Основная теорема теории игр Дж. фон Неймана
Наборы вероятностей (частот)
первого игрока
второго игрока
Каждая конечная игра имеет по крайней мере одно оптимальное решение в смешанных стратегиях.
Слайд 31. Геометрическое решение игр 2×2, 2×n, m×2
1.1. Геометрическое решение игры
2×2
1.2. Геометрическое решение игры 2×n
1.3. Геометрическое решение игры m×2
Слайд 4Графический метод решения игры
1.1. Геометрическое решение игры 2×2
Этап 1. В декартовой
системе координат pOH по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка р=0) соответствует стратегии
, правый – стратегии
Промежуточные точки оси абсцисс соответствуют вероятностям некоторых смешанных стратегий
(р=1).
Этап 2. На левой оси – оси ординат, откладываются выигрыши стратегии
Этап 3. На линии, параллельной оси ординат, из точки 1 откладываются
выигрыши стратегии
Этап 4. Соединяем точки
прямой
, точки
прямой
Слайд 6Для уточнения и проверки результатов графического решения можно дополнительно решить системы
для первого игрока
для второго игрока
Слайд 11
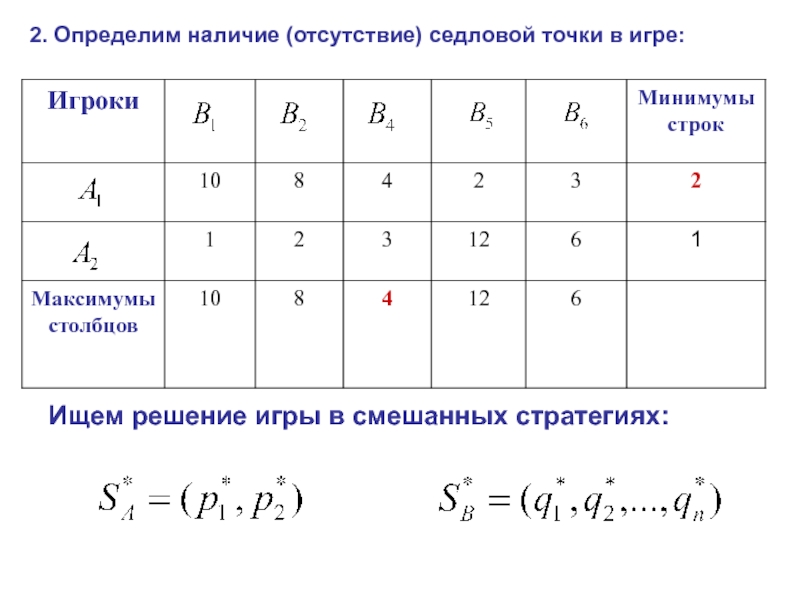
2. Определим наличие (отсутствие) седловой точки в игре:
Ищем решение игры в
смешанных стратегиях:
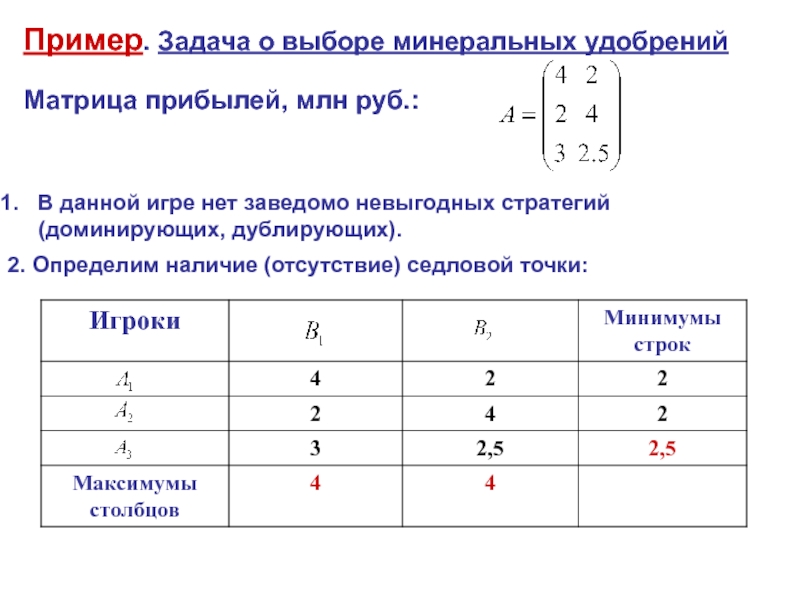
Слайд 16Пример. Задача о выборе минеральных удобрений
Матрица прибылей, млн руб.:
В данной игре
нет заведомо невыгодных стратегий
(доминирующих, дублирующих).
(доминирующих, дублирующих).
2. Определим наличие (отсутствие) седловой точки:
Слайд 19Общая схема решения игр 2×n и m×2
Строят прямые, соответствующие стратегиям
игрока В или А.
2. Находят две стратегии игрока В или А, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой. Эти стратегии являются активными в оптимальной смешанной стратегии игрока В или А.
3. Находят координаты точки пересечения, тем самым определяя оптимальную стратегию игрока А или В и цену игры.
4. Оптимальную стратегию другого игрока находят, решая систему уравнений, включающую его активные стратегии.
2. Находят две стратегии игрока В или А, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой. Эти стратегии являются активными в оптимальной смешанной стратегии игрока В или А.
3. Находят координаты точки пересечения, тем самым определяя оптимальную стратегию игрока А или В и цену игры.
4. Оптимальную стратегию другого игрока находят, решая систему уравнений, включающую его активные стратегии.
Слайд 202. Приведение антагонистической игры к паре
взаимно двойственных задач линейного программирования
Игра
порядка
Слайд 24При решении произвольной конечной игры размера
рекомендуется придерживаться следующей схемы:
Исключить из платежной матрицы заведомо невыгодные стратегии.
2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена игры совпадает с верхней (нижней) ценой.
3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Игры размера решаются путем сведения к паре взаимно двойственных задач линейного программирования. Для игр размера , возможно применить графо-аналитический метод решения.
или
