- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение геометрических задач при подготовке к ЕГЭ презентация
Содержание
- 1. Решение геометрических задач при подготовке к ЕГЭ
- 2. Содержание 1. Справочная информация. 2. Задания диагностических
- 3. СПРАВОЧНАЯ ИНФОРМАЦИЯ
- 4. СПРАВОЧНАЯ ИНФОРМАЦИЯ треугольники четырехугольники правильные многоугольники окружность векторы
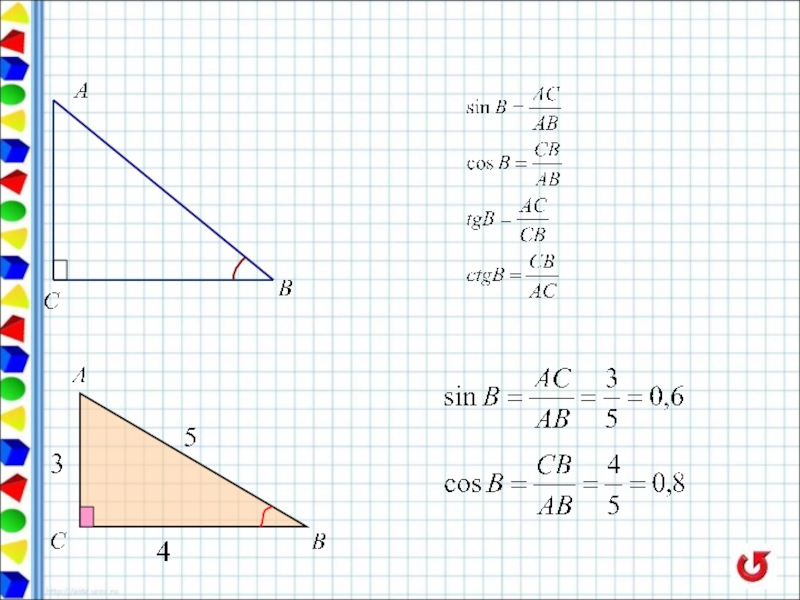
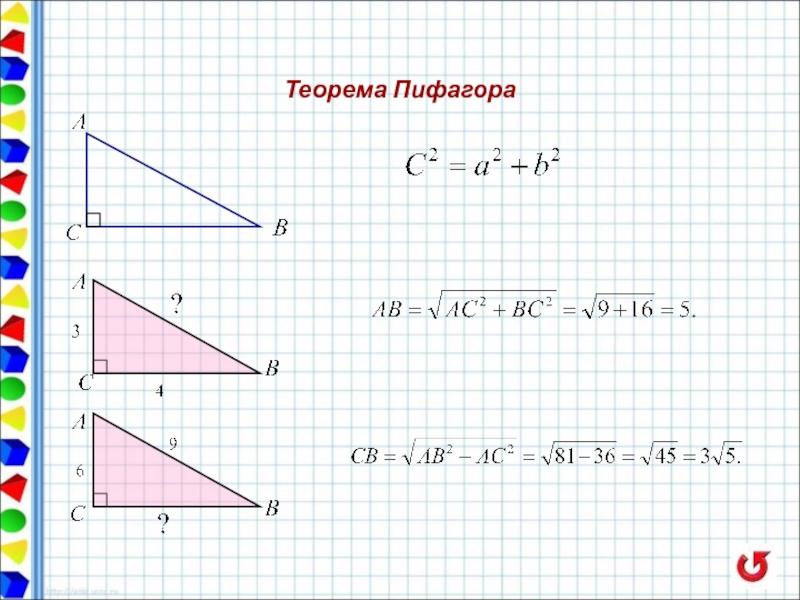
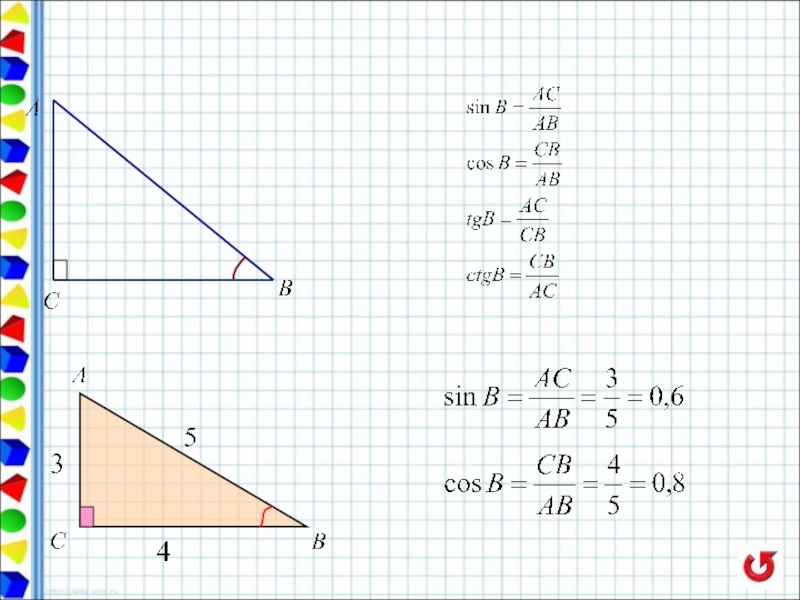
- 6. Справочные сведения Треугольники
- 7. Справочные сведения Треугольники
- 9. Справочные сведения Четырехугольники
- 10. Справочные сведения Четырехугольники
- 11. Справочные сведения Четырехугольники
- 12. Справочные сведения Четырехугольники
- 14. Справочные сведения Четырехугольники
- 15. Справочные сведения Правильные многоугольники
- 16. Примеры равнобедренных
- 17. Справочные сведения Окружность
- 18. Справочные сведения Окружность
- 19. Справочные сведения Окружность
- 20. Справочные сведения Окружность
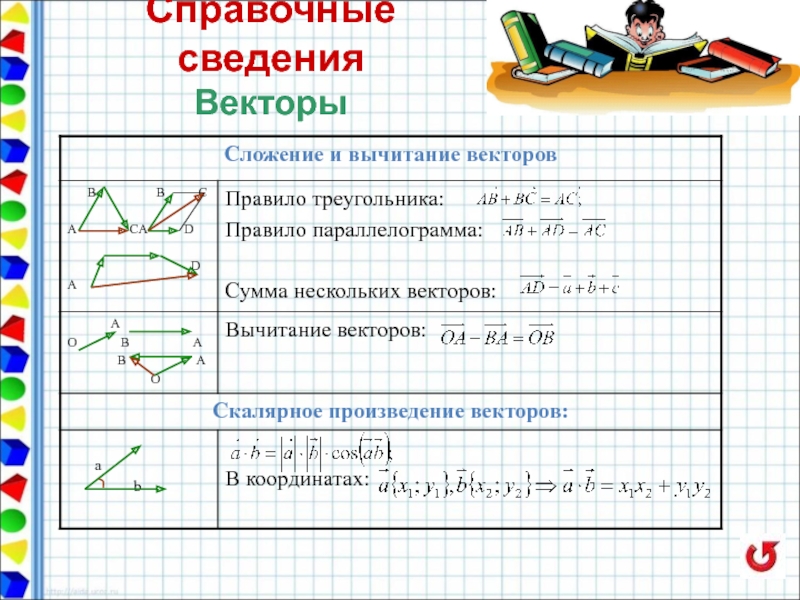
- 21. Справочные сведения Векторы
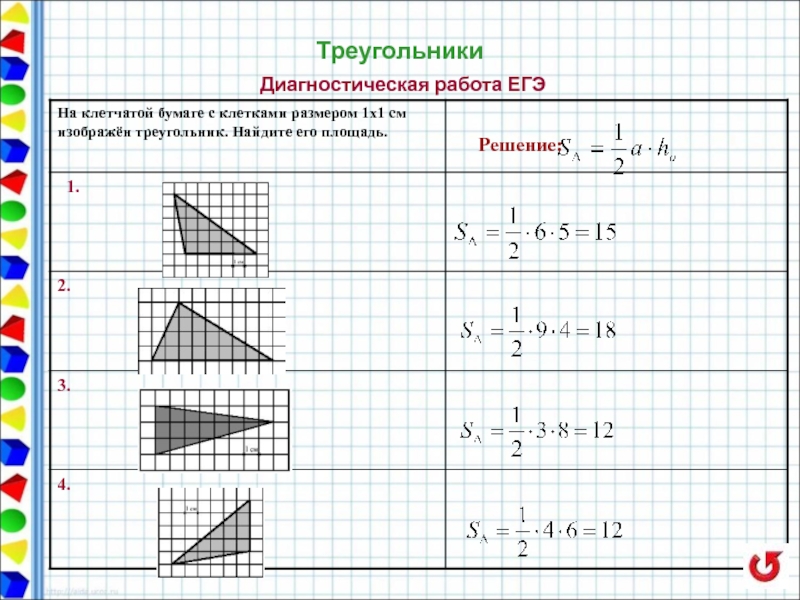
- 22. Треугольники
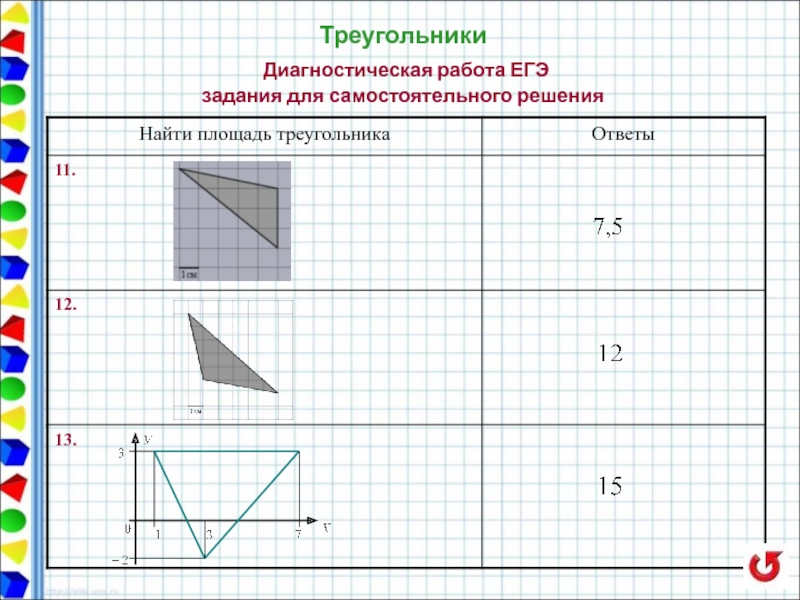
- 23. Треугольники Диагностическая работа ЕГЭ задания
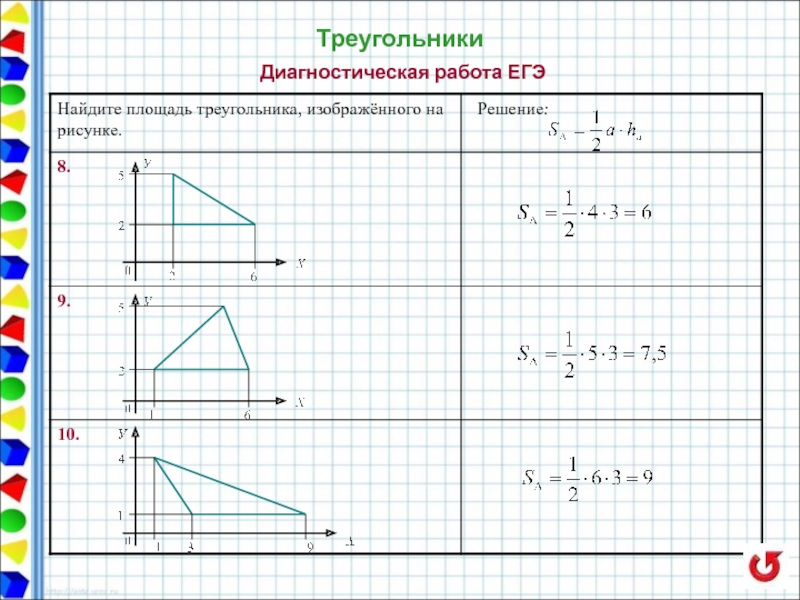
- 24. Треугольники Диагностическая работа ЕГЭ
- 25. Треу0гольники Диагностическая работа ЕГЭ
- 26. Треугольники Диагностическая работа ЕГЭ
- 27. Треугольники Диагностическая работа ЕГЭ задания
- 28. Треугольники 1. Площадь параллелограмма
- 29. Треугольники Задачи 11 (ЕГЭ 2015) для самостоятельного
- 30. Диагностическая работа ЕГЭ С -2.1
- 31. Тренировочный вариант С – 2.2
- 32. Диагностическая работа ЕГЭ С – 2.3
- 33. Треугольники Диагностическая работа ЕГЭ задания
- 34. Спасибо за внимание!
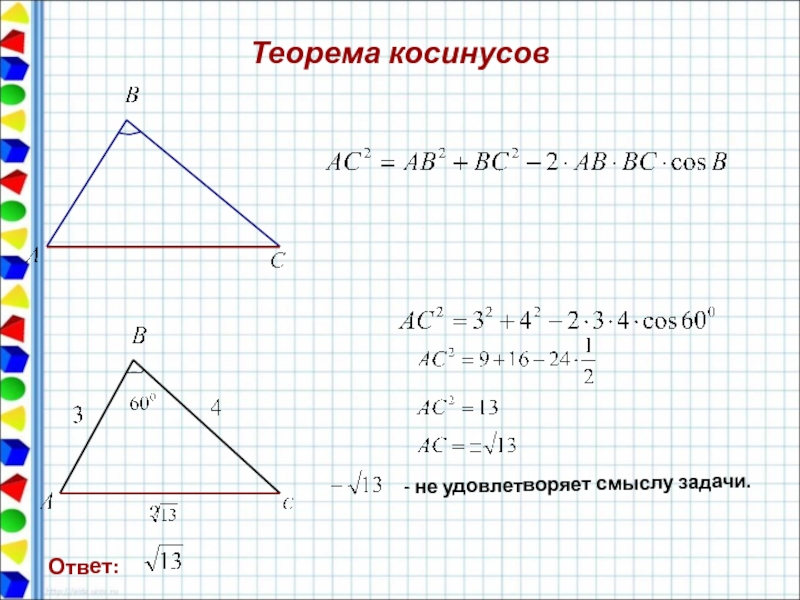
- 35. Теорема косинусов
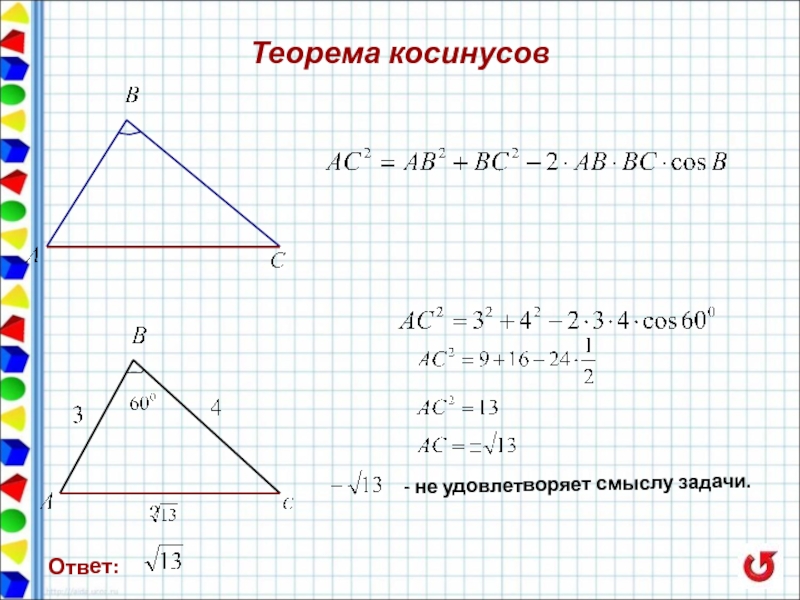
- 37. Теорема косинусов
Слайд 2Содержание
1. Справочная информация.
2. Задания диагностических работ по типу ЕГЭ:
- В4; для самостоятельного решения
- В 6;
- В 6; для самостоятельного решения
- В 11;
- В 11; для самостоятельного решения
- С 2;
- С 2; для самостоятельного решения
Слайд 16
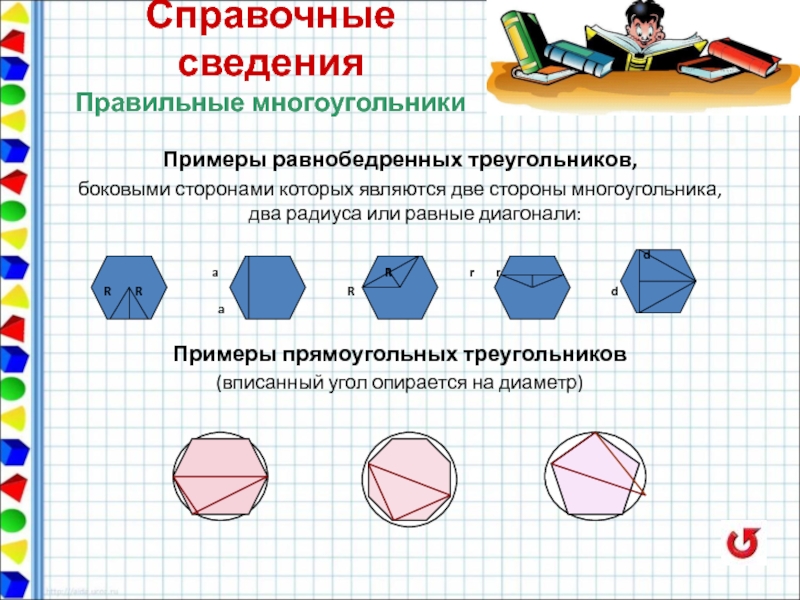
Примеры равнобедренных треугольников,
боковыми сторонами которых являются две стороны многоугольника, два
d
a R r r
R R R d
a
Примеры прямоугольных треугольников
(вписанный угол опирается на диаметр)
Справочные сведения
Правильные многоугольники
Слайд 28Треугольники
1. Площадь параллелограмма АВСD равна 16, диагональ АС равна 2,
Решение:
1. SACD = 0,5∙SABCD = 0,5∙16 = 8
SACD = 0,5∙AC∙CD∙sin
2. По свойству параллелограмма: ВC = AD
По теореме косинусов:
-10 не удовлетворяет смыслу задачи.
Ответ: 10.
Слайд 29Треугольники
Задачи 11 (ЕГЭ 2015) для самостоятельного решения
1. Точка О является центром
АВС. Найдите площадь треугольника АОС, если известно, что ВС = 6,
(Ответ: 18)
2. В равнобедренный прямоугольный треугольник с катетом, равным 1,
вписан квадрат, имеющий с треугольником общий прямой угол.
Найдите периметр квадрата.
(Ответ: 2)
3. В равнобедренном треугольнике синус угла при основании равен 0,8, а
радиус вписанной окружности равен 6. Найдите периметр данного
треугольника.
(Ответ: 64)
4. В равнобедренном треугольнике АВС, с основанием АС медиана ВМ и
высота СН пересекаются в точке К. Найдите площадь треугольника АВС,
если известно, что СК = 1, а косинус угла при вершине В равен 0,8.
(Ответ:2,7)
Слайд 30
Диагностическая работа ЕГЭ
С -2.1 В прямоугольном параллелепипеде ABCDA1В1C1D1, у которого
BC = 6, CC1 = 4, найдите тангенс угла между плоскостями АCD1 и А1В1С1.
Решение:
1) Вместо плоскости А1В1С1 возьмём параллельную ей
плоскость АВС.
2) Пусть Е – середина АС.
- линейный угол искомого угла.
3) Из прямоугольного треугольника D1DE находим:
Ответ:
Слайд 31Тренировочный вариант
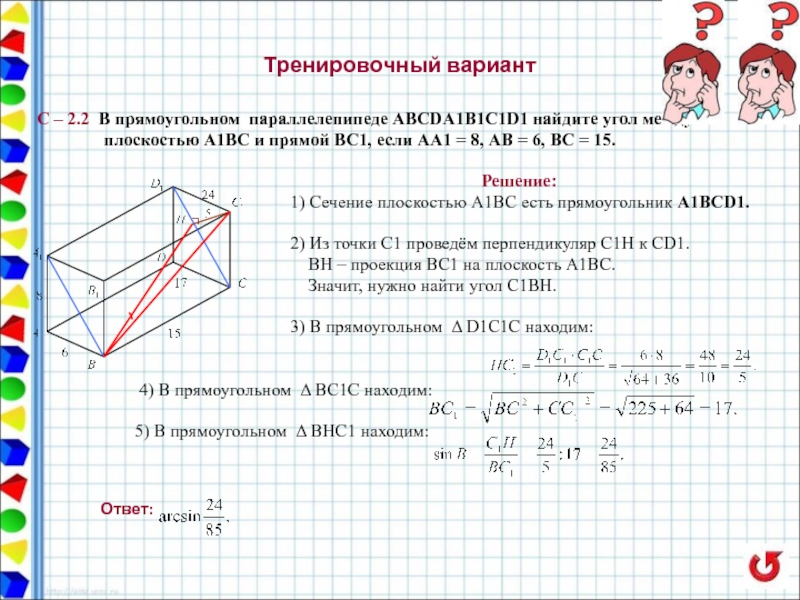
С – 2.2 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите
плоскостью А1ВС и прямой ВС1, если АА1 = 8, АВ = 6, ВС = 15.
Решение:
1) Сечение плоскостью А1ВС есть прямоугольник A1BCD1.
2) Из точки С1 проведём перпендикуляр С1Н к СD1.
ВН – проекция ВС1 на плоскость А1ВС.
Значит, нужно найти угол С1ВН.
3) В прямоугольном Δ D1C1C находим:
4) В прямоугольном Δ ВC1C находим:
5) В прямоугольном Δ ВНC1 находим:
Ответ:
Слайд 32Диагностическая работа ЕГЭ
С – 2.3 В кубе ABCDA1B1C1D1
Решение:
1) Построим отрезки СD1 и АС.
2) Искомое расстояние равно длине
перпендикуляра СН, проведённого к прямой АD1.
Этот перпендикуляр является медианой равностороннего треугольника АСD1 со стороной
3)
Ответ:
Слайд 33Треугольники
Диагностическая работа ЕГЭ
задания для самостоятельного решения
С – 2.4 В
Ответ:
С – 2.5 В кубе ABCDA1B1C1D1 все рёбра равны 1. Найдите расстояние от точки С до прямой ВD1.
Ответ:
С – 2.6 В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB = 4, BC = 6, CC1 = 4, найдите тангенс угла между плоскостями CDD1 и BDA1.
Ответ: