?
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение геометрических задач при подготовке к ГИА презентация
Содержание
- 1. Решение геометрических задач при подготовке к ГИА
- 2. Содержание 1. Справочная информация. 2. Задания
- 3. СПРАВОЧНАЯ ИНФОРМАЦИЯ
- 4. треугольники четырехугольники правильные многоугольники окружность векторы СПРАВОЧНАЯ ИНФОРМАЦИЯ
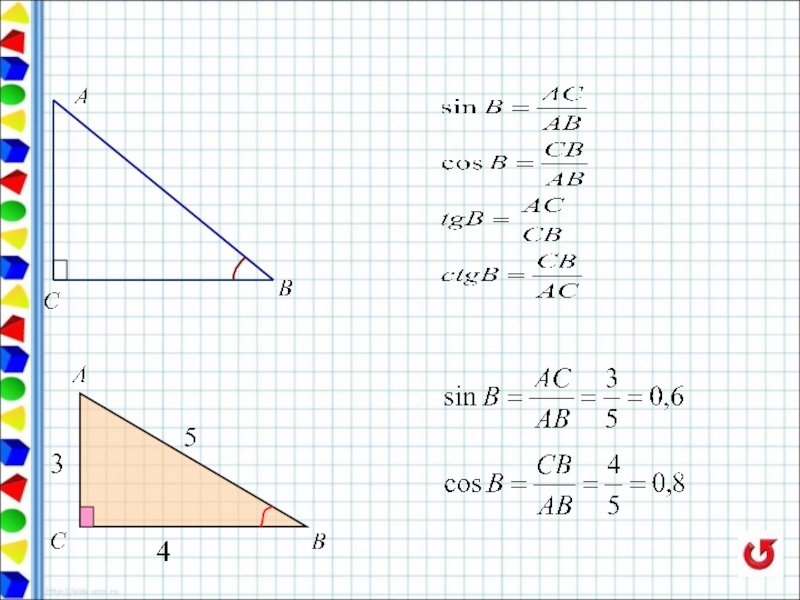
- 6. Справочные сведения Треугольники
- 7. Справочные сведения Треугольники
- 9. Справочные сведения Четырехугольники
- 10. Справочные сведения Четырехугольники
- 11. Справочные сведения Четырехугольники
- 12. Справочные сведения Четырехугольники
- 14. Справочные сведения Четырехугольники
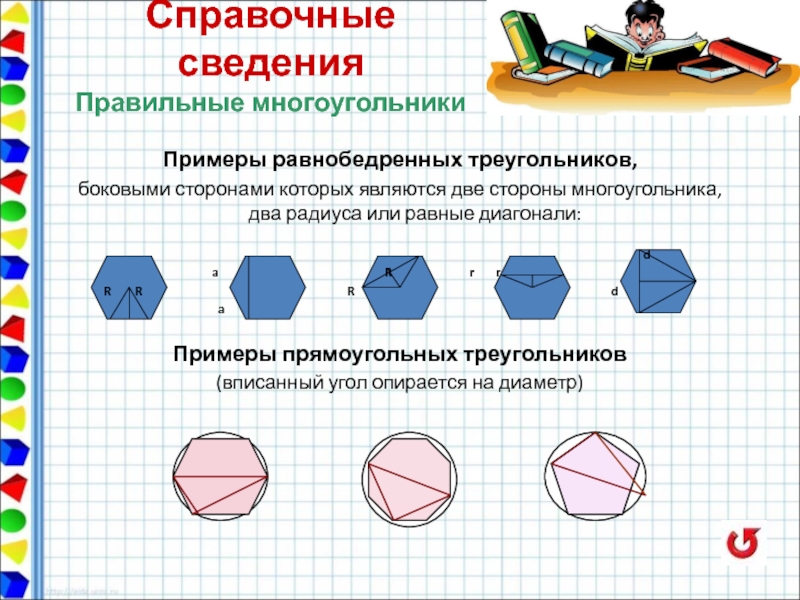
- 15. Справочные сведения Правильные многоугольники
- 16. Примеры равнобедренных
- 17. Справочные сведения Окружность
- 18. Справочные сведения Окружность
- 19. Справочные сведения Окружность
- 20. Справочные сведения Окружность
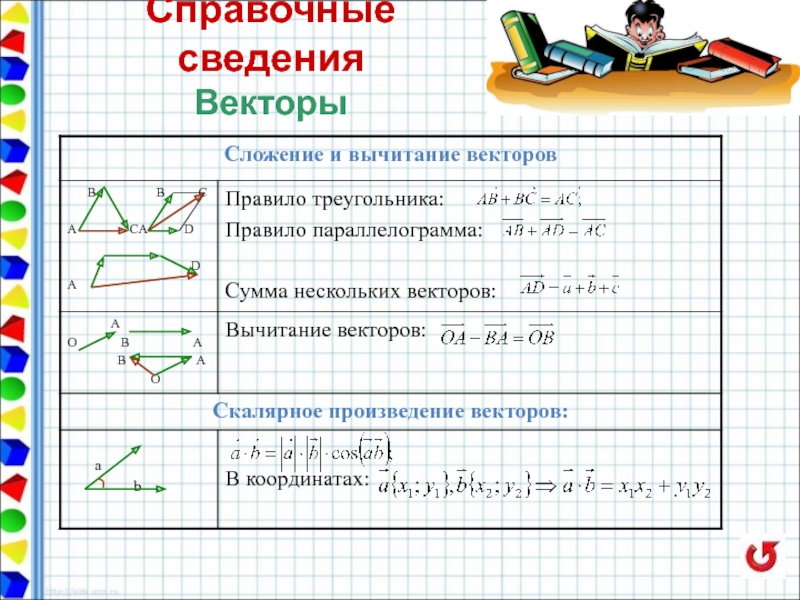
- 21. Справочные сведения Векторы
- 22. Треугольники
- 23. Треугольники
- 24. Треугольники
- 25. Треугольники
- 26. Треугольники
- 27. Треугольники
- 28. Задачи на вычисления в равнобедренном треугольнике,
- 29. 1. Найдите основание равнобедренного треугольника, если оно
- 30. Треугольники Решение заданий второй части 2.
- 31. Треугольники Решение заданий второй части 2.
- 32. Треугольники Решение заданий второй части Свойство
- 33. Треугольники Решение заданий второй части В задачах
- 34. Треугольники Решение заданий второй части 4. Площадь
- 35. Треугольники Решение заданий второй части 5.
- 36. Треугольники Решение заданий второй части 6. Укажите,
- 37. Треугольники Решение заданий второй части (с практическим
- 38. Треугольники Решение заданий второй части (с
- 39. Треугольники Решение заданий второй части (с
- 40. По окончании измерений инженер составил следующую запись:
- 41. Треугольники Решение заданий второй части
- 42. Треугольники Решение заданий второй части 3
- 43. Треугольники Решение заданий второй части (с
- 44. Треугольники Решение заданий второй части (с практическим
- 45. Треугольники Решение заданий второй части (с
- 46. Треугольники Решение заданий второй части 3.
- 47. Треугольники Решение заданий второй части 4.
- 48. Треугольники Решение заданий второй части 5.
- 49. Треугольники Решение заданий второй части (с
- 50. Треугольники Решение заданий второй части В).Чтобы
- 51. Треугольники Решение заданий второй части (с
- 52. Треугольники Решение заданий второй части (с
- 53. Треугольники Решение заданий второй части (для
- 54. Треугольники Решение заданий второй части (для самостоятельного
- 55. Задания с развёрнутым свободным ответом Используются во
- 56. Треугольники Решение заданий второй части 15.
- 57. Треугольники Решение заданий третьей части Основную трудность
- 58. Треугольники Решение заданий третьей части (ГИА –
- 59. Треугольники Решение заданий третьей части 2. (ГИА
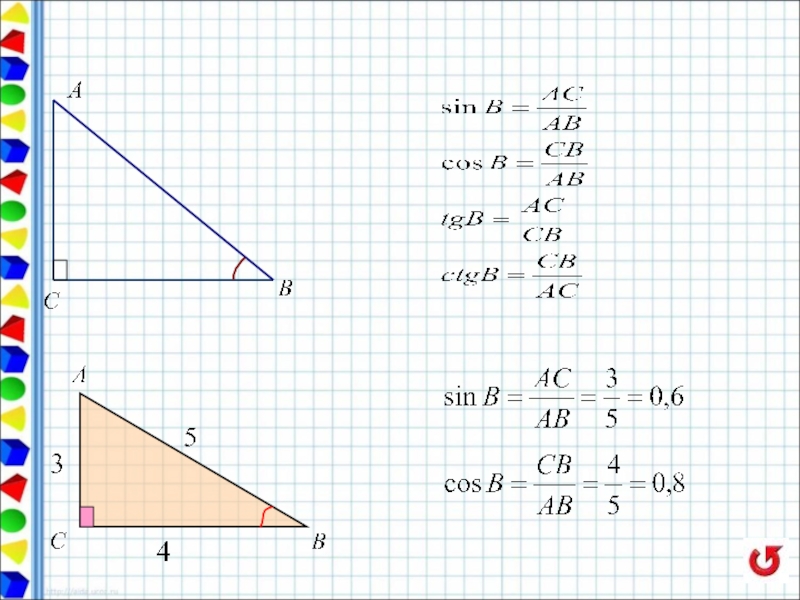
- 60. Теорема косинусов
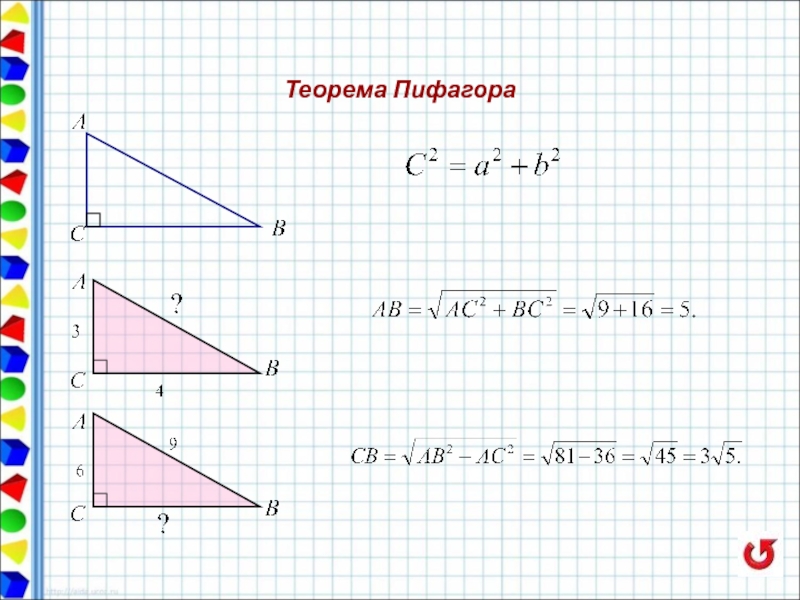
- 64. Теорема Пифагора
Слайд 2Содержание
1. Справочная информация.
2. Задания первой части ГИА.
3. Задания второй части ГИА.
- с практическим содержанием;
для самостоятельного решения;
- с развёрнутым свободным ответом.
4. Задания третьей части ГИА.
5. Задания ЕГЭ 2009 (В-11).
для самостоятельного решения
Слайд 16
Примеры равнобедренных треугольников,
боковыми сторонами которых являются две стороны многоугольника, два
d
a R r r
R R R d
a
Примеры прямоугольных треугольников
(вписанный угол опирается на диаметр)
Справочные сведения
Правильные многоугольники
Слайд 28 Задачи на вычисления в равнобедренном треугольнике, как правило, помимо свойств,
ся к равнобедренному треугольнику, используют свойства прямоугольного треугольника, т. к.
медиана, проведённая к основанию, делит равнобедренный треугольник на два прямоугольных.
1. Найдите основание равнобедренного треугольника, если оно в 3 раза меньше
боковой стороны, а медиана, проведённая к боковой стороне, равна .
Решение: 1 способ
1) Обозначим АС = х, тогда ВС = 3х, МС = 1,5х.
2) : по теореме косинусов
3) Пусть ВН – высота к основанию АС.
4) Получаем:
- 6 не удовл. смыслу задачи
Отсюда АС = 6.
Ответ: 6.
Треугольники
Решение заданий второй части
Слайд 291. Найдите основание равнобедренного треугольника, если оно в 3 раза меньше
стороны, а медиана, проведённая к боковой стороне, равна .
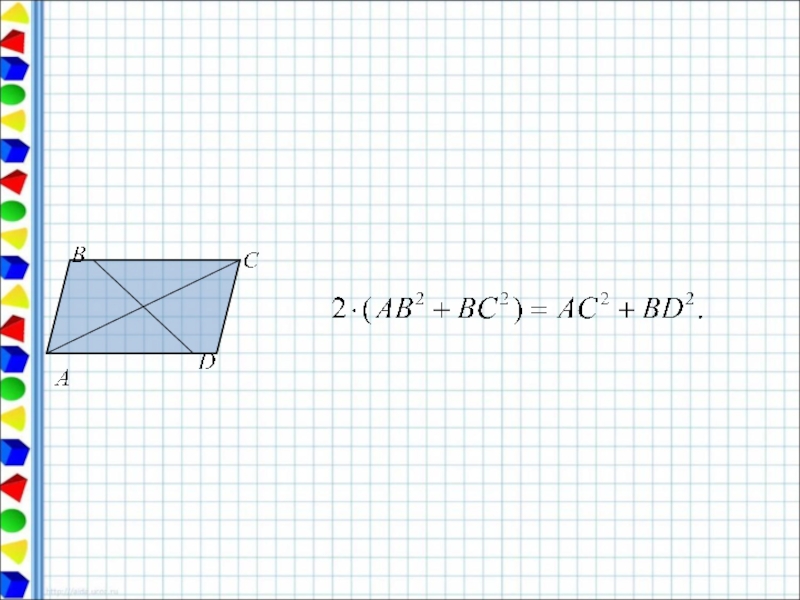
2 способ: используется приём, позволяющий быстро решать задачи, где речь идёт о медиане.
Медиана АМ продлевается за точку М и на её продолжении откладывается отрезок МD, равный
медиане.
Рассматривается параллелограмм АВDС и используется формула, связывающая его
стороны и диагонали.
Решение:
1) Пусть АС – основание треугольника, АМ – медиана.
Отложим на луче АМ отрезок МD = АМ
Тогда АСВD – параллелограмм, т. к.его диагонали пересекаются
в середине.
2) Обозначим АС = х, АВ = ВС = 3х, тогда по свойству сторон и
диагоналей параллелограмма имеем: ,
или
Ответ: 6.
Треугольники
Решение заданий второй части
Слайд 30Треугольники
Решение заданий второй части
2. В окружность с радиусом 13 вписан равнобедренный
угла при основании треугольника равен . Радиус ОМ пересекает под прямым углом
боковую сторону в точке К. Найдите длину отрезка ОК.
1 способ опирается на свойства вписанных и центральных углов и решение прямоугольных
треугольников.
Решение:
1) Угол при основании равнобедренного треугольника может быть только
острым, значит, центр О с вершиной А лежит по одну сторону от хорды ВС.
Тогда - центральный, соответствующий углу А. Отсюда
2) Δ ВОС – равнобедренный, ОК – высота, проведённая к основанию, тогда ОК – биссектриса угла О, отсюда имеем:
3)
Ответ: 5.
Слайд 31Треугольники
Решение заданий второй части
2. В окружность с радиусом 13 вписан равнобедренный
угла при основании треугольника равен . Радиус ОМ пересекает под прямым углом
боковую сторону в точке К. Найдите длину отрезка ОК.
Т.к. в ряде случаев первый способ применить бывает невозможно, приведём 2 способ реше-
ния, который использует свойство отрезков хорд.
Решение:
1)
2)
3) Достроим радиус ОМ до диаметра РМ, тогда РМ =26.
Пусть МК = х. По свойству отрезков хорд получим
Ответ:5.
Слайд 32Треугольники
Решение заданий второй части
Свойство отрезков касательных чаще всего применяют в задачах,
элементов равнобедренных или прямоугольных треугольников. При решении задач бывает
полезно отметить на рисунке точки касания и отметить равные отрезки одинаковыми буквами
или чёрточками, используя при этом свойства рассматриваемого треугольника.
3. Окружность с центром О, вписана в равнобедренный треугольник АВС с основанием АС.
Она касается стороны ВС в точке М, причём отрезок ВМ составляет 0,4 боковой стороны.
Найдите высоту, проведённую к боковой стороне, если АС = 30.
Решение:
1) Обозначим буквой Н точку касания вписанной окружности с основанием.
Так как ΔАВС – равнобедренный, то центр О лежит на высоте к основанию,
т. е. ВН – высота и Н – середина основания.
2) Если считать ВМ = 2х и СМ = 3х, то АВ = ВС = 5х.
По свойству отрезков касательных имеем СН = 3х, 3х = 15, АВ = 25.
3) По теореме Пифагора
4) SАВС =0,5 ВН· АС = 0,5 АВ · h, отсюда h = (20 · 30) : 25 = 24.
Ответ: 24.
Слайд 33Треугольники
Решение заданий второй части
В задачах на площадь треугольника иногда используется отношение
треугольников. Отношение площадей подобных треугольников равно квадрату
отношения сходственных сторон (или квадрату коэффициента подобия).
Из формулы площади треугольника можно вывести ещё два следствия:
- если треугольники имеют общее основание (или равные основания), то их
площади относятся, как высоты, проведённые к этим основаниям;
- если треугольники имеют общую высоту (или равные высоты), то их площади
относятся, как основания.
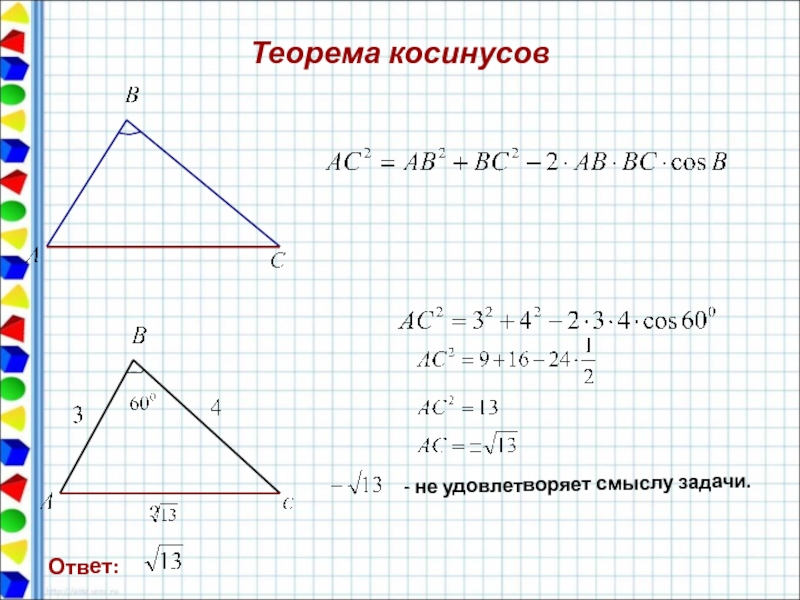
Слайд 34Треугольники
Решение заданий второй части
4. Площадь треугольника МРК равна 21. Известно, что
РА = , а в треугольнике АРМ сторона АМ – наименьшая. Найдите сторону МК.
Решение:
1)
2)
Т. к. МА – наименьшая сторона в треугольнике АРМ, то α не
может быть тупым, α = .
3) В треугольнике МАР по теореме косинусов:
Ответ: 10.
Слайд 35Треугольники
Решение заданий второй части
5. В прямоугольном треугольнике АВС с прямым
Решение:
1) По свойству биссектрисы треугольника
Тогда АВ = 5х, ВС = 4х,
2) (т. к. эти треугольники имеют одну
и ту же высоту ВС).
Значит,
Ответ: 270.
Слайд 36Треугольники
Решение заданий второй части
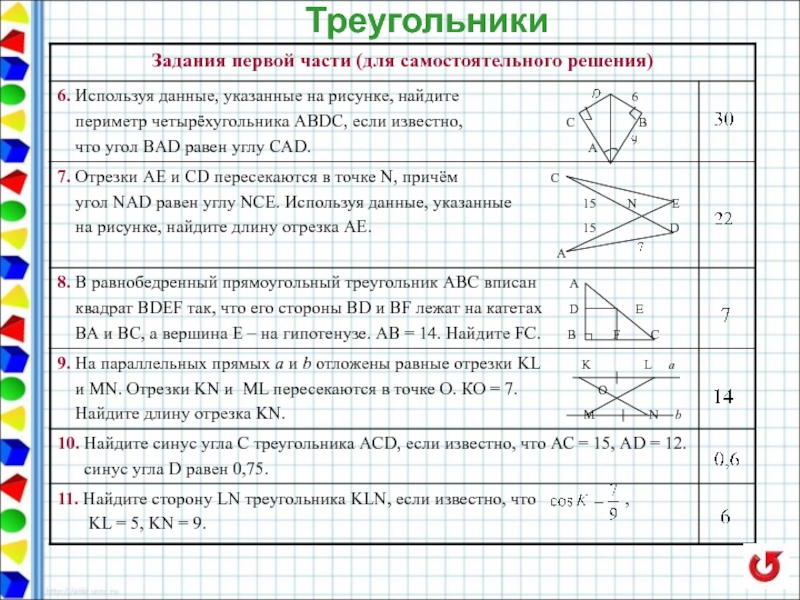
6. Укажите, какие из перечисленных ниже утверждений верны.
1)
2) Медиана проходит через середину стороны треугольника.
3) Медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине.
4) Точка пересечения медиан произвольного треугольника – центр окружности, описан –
ной около этого треугольника.
5) Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в
отношении 2 к 1, считая от вершины.
Ответ: 2), 3), 5).
7. Укажите, какие из перечисленных ниже утверждений верны.
1) Биссектриса всегда проходит через середину стороны треугольника.
2) Биссектриса всегда делит пополам один из углов треугольника.
3) Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные
двум другим сторонам.
4) Точка пересечения биссектрис произвольного треугольника – центр окружности, вписанной
в этот треугольник.
5) Точка пересечения биссектрис произвольного треугольника – центр окружности, описанной
около этого треугольника.
Ответ: 2), 3), 4).
Слайд 37Треугольники
Решение заданий второй части
(с практическим содержанием)
8. Из листа фанеры вырезали равносторонний
12 дм. Сколько килограммов краски потребуется, чтобы его покрасить, если на
поверхности расходуется 0,015 кг краски?
Решение:
По формуле Герона получаем:
Расход краски равен 48 · 0,015 = 0,72 (кг)
Ответ: 0, 72.
Слайд 38Треугольники
Решение заданий второй части
(с практическим содержанием)
буквы этого языка – круги, треугольники
и иные математические фигуры.
(Галилей)
Измерение высоты предмета.
1 способ самый лёгкий и самый древний – по тени предмета, использующий:
а) свойства равнобедренного треугольника. Для этого выбирается час, когда длина
тени человека равна его росту; в этот момент высота предмета равна длине отбрасы-
ваемой им тени.
Б) подобие треугольников. Можно пользоваться любой
тенью, любой длины. Измерив свою тень или тень любого
шеста, вычисляют искомую высоту из пропорции:
АВ : ав = ВС : вс.
(Высота дерева во столько же раз больше вашей собствен-
ной высоты (или шеста), во сколько раз тень дерева длин-
нее вашей (или шеста).
Слайд 39Треугольники
Решение заданий второй части
(с практическим содержанием)
2 способ
А) С помощью шеста,
равнялась вашему росту. Место для шеста надо выбрать так, чтобы, лёжа вы видели
верхушку дерева на одной прямой линии с верхней точкой шеста. По свойству равно-
бедренного прямоугольного треугольника АВ = ВС, т. е. высоте дерева.
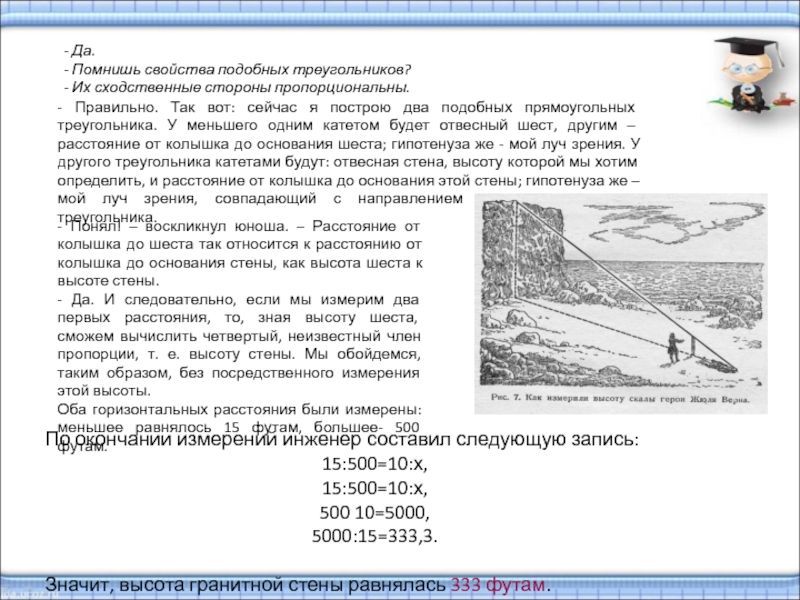
Слайд 40По окончании измерений инженер составил следующую запись:
15:500=10:х,
15:500=10:х,
500 10=5000,
5000:15=333,3.
Значит, высота гранитной стены
- Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же - мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника.
- Понял! – воскликнул юноша. – Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены.
- Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены. Мы обойдемся, таким образом, без посредственного измерения этой высоты.
Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее- 500 футам.
- Да.
- Помнишь свойства подобных треугольников?
- Их сходственные стороны пропорциональны.
Слайд 41Треугольники
Решение заданий второй части
(с практическим содержанием)
Б) (способ Жюля Верна,
Для определения высоты скалы необходимо взять шест длиной равной росту человека, воткнуть вертикально в землю. Затем отойти от скалы на такое расстояние, чтобы лёжа на песке, можно было видеть и конец шеста и конец гребня.
В учебнике этот способ рассматривается в п.64 «Практические приложения подобия
треугольников»
Слайд 42Треугольники
Решение заданий второй части
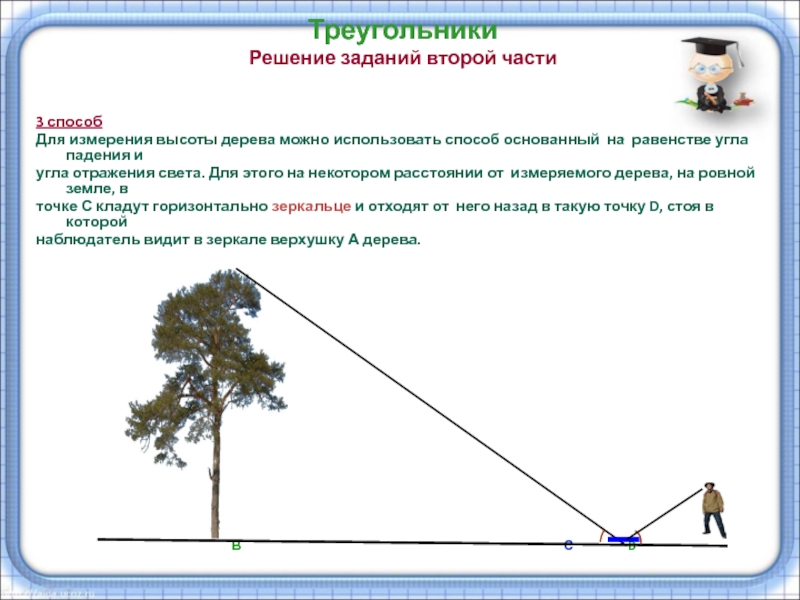
3 способ
Для измерения высоты дерева можно использовать
угла отражения света. Для этого на некотором расстоянии от измеряемого дерева, на ровной земле, в
точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой
наблюдатель видит в зеркале верхушку А дерева.
А
В С D
Слайд 43Треугольники
Решение заданий второй части
(с практическим содержанием)
Как поступать, если к
А) Задача решается двукратным применением описанного выше способа – помещение зеркала
высота равна возвышению глаза наблюдателя, умноженному на отношение расстояния между
положениями зеркала к разности расстояний наблюдателя от зеркала.
Б) На прямой, проходящей через основание Н предмета, отмечают точки В и С на определён-
ном расстоянии а друг от друга и измеряют углы АВН и АСВ:
По теореме синусов:
Способ рассматривается в учебнике п.100,
«Измерительные работы».
Задача № 1036, 1038.
Слайд 44Треугольники
Решение заданий второй части (с практическим содержанием)
1. В 40 м одна
Решение:
По теореме Пифагора расстояние АВ между
верхушками сосен равно
Ответ: 47 м.
Слайд 45Треугольники
Решение заданий второй части
(с практическим содержанием)
2. Тень ВС от отвесного
момент высота Солнца над горизонтом, т. е. как велик угол С?
Решение:
Ответ:
Слайд 46Треугольники
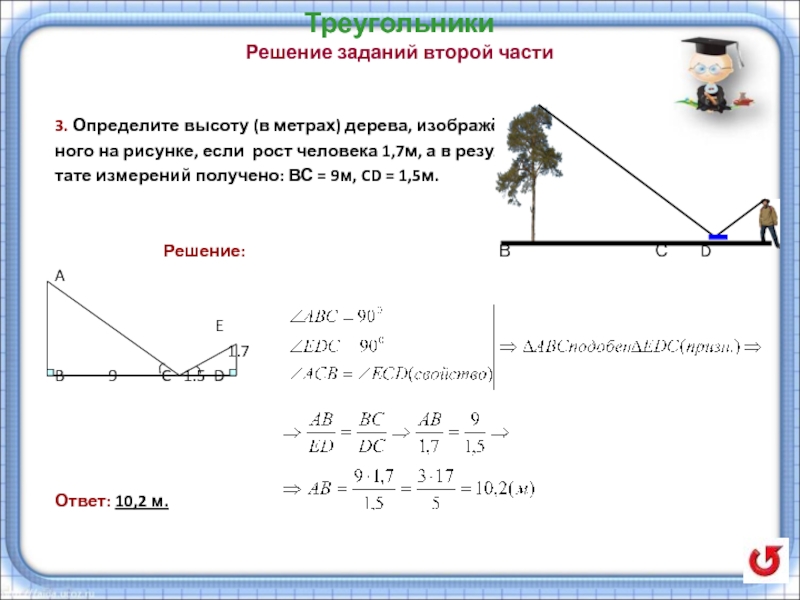
Решение заданий второй части
3. Определите высоту (в метрах) дерева, изображён –
ного
тате измерений получено: ВС = 9м, CD = 1,5м.
Решение: В С D
A
E
1.7
B 9 C 1.5 D
Ответ: 10,2 м.
Слайд 47Треугольники
Решение заданий второй части
4. Для измерения высоты дома нужно воткнуть в
выше роста наблюдателя на расстоянии от дома. Затем следует
отойти от шеста назад по продолжению до той точки О, с которой
можно увидеть высшую точку М на одной линии с верхней О N
точкой шеста. Далее, стоя на том же месте, необходимо P
отметить на шесте и на доме 2 точки и N, лежащие на горизонтальной прямой.
Определите высоту МР дома, если рост человека
Решение:
1)
подобен по первому признаку
Отсюда следует пропорциональность сторон:
MP = MN + NP = 6 + 1,7 = 7,7 (м).
Ответ: 7,7 м.
Слайд 48Треугольники
Решение заданий второй части
5. Для того, чтобы измерить высоту CD =
инструментов измерить угол α, под которым видна вершина С холма из точки А, затем
отойти на расстояние АВ = d, находясь в плоскости ACD, и измерить угол β, под которым
видна вершина С. - рост наблюдателя. Найдите высоту холма, если
.
С Решение:
1)
β α как стороны прямоугольников
2)
3)
4) В прямоугольном
5)
Ответ: 88,3м.
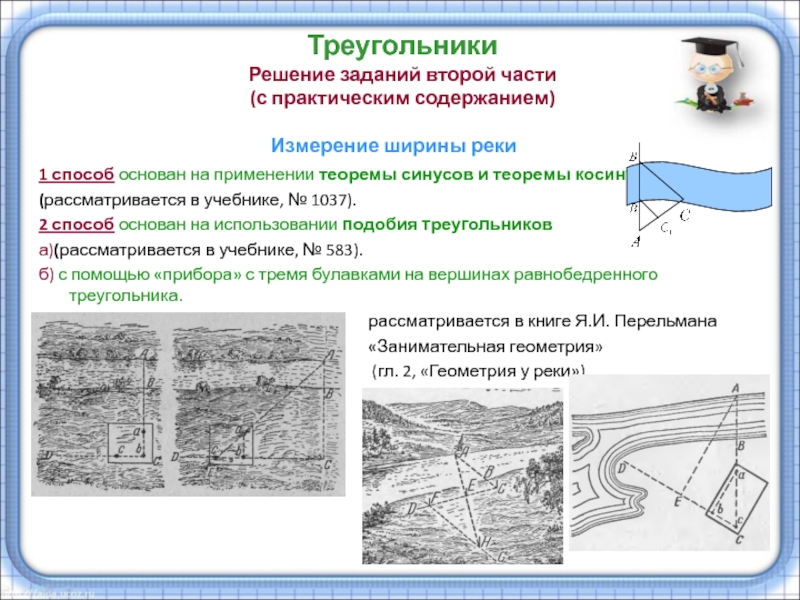
Слайд 49Треугольники
Решение заданий второй части
(с практическим содержанием)
1 способ основан на применении теоремы синусов и теоремы косинусов.
(рассматривается в учебнике, № 1037).
2 способ основан на использовании подобия треугольников
а)(рассматривается в учебнике, № 583).
б) с помощью «прибора» с тремя булавками на вершинах равнобедренного треугольника.
рассматривается в книге Я.И. Перельмана
«Занимательная геометрия»
(гл. 2, «Геометрия у реки»)
Слайд 50Треугольники
Решение заданий второй части
В).Чтобы измерить ширину реки на её прямолинейном участке,
ном берегу выбрать какой – либо ориентир, например, камень (точка С). Затем на своём берегу
следует найти точку А, так, чтобы отрезок АС был перпендикулярен береговой линии (это
можно сделать с помощью угломерных инструментов). Далее нужно отметить точку В, нахо –
дящуюся на расстоянии АВ = d от точки А и отойти от неё в точку D так, чтобы С, В и D нахо –
дились на одной прямой линии. Затем необходимо отметить точку Е так, чтобы С, А и Е нахо –
дились на одной прямой и отрезок ED был параллелен береговой линии.
6. Найдите ширину реки АС = Н, если АВ = = 24 м, ED = = 30 м, АЕ = h = 4,5 м.
Решение:
по первому признаку подобия
( по построению).
Отсюда
Подставив в формулу числа, данные в условии, получим:
Ответ: 18.
Слайд 51Треугольники
Решение заданий второй части
(с практическим содержанием)
7. Чтобы определить ширину АВ
к западу на , а ВС – к востоку на . Длина ВС = 68 м, АС = 35 м. Вычислить по
этим данным ширину озера.
Решение:
1) В треугольнике АВС:
2) Опускаем высоту АD, имеем
3)
4) Из треугольника АВD имеем:
Ответ: 49 м. (способ предложен в книге Я. И. Перельмана «Занимательная геометрия»)
!? Найдите более простой способ решения задачи.
Слайд 52Треугольники
Решение заданий второй части
(с практическим содержанием)
1 способ
основан на применении теоремы синусов и теоремы косинусов. На местности выбираем точку
В и измеряем длину с отрезка АВ. Измеряются углы А и В:
По теореме синусов находим искомое расстояние d:
Способ рассматривается в
учебнике п.100,
«Измерительные работы».
Задача № 1037.
2 способ основан на использовании подобия треугольников
(рассматривается в учебнике, № 582).
Слайд 55Задания с развёрнутым свободным ответом
Используются во второй и третьей частях работы
сложных предметных умений – анализировать ситуацию, разрабатывать способ
решения, проводить математически грамотные рассуждения.
Характеризуя высокий уровень подготовки по предмету, как правило, выделяют
следующие его качества:
умение выполнять чертёж, соответствующий ситуации, представленной в условии задачи;
прочное владение системой знаний, указанных в школьной программе;
умение обосновывать сделанные выводы ссылкой на теоремы и определения;
умение строить логически верную цепочку доказательных рассуждений, шагов
решения , которые помогают прийти к требуемому выводу;
умение синтезировать информацию из различных разделов курса геометрии для решения поставленной проблемы;
умение математически грамотно записать решение задачи.
Слайд 56Треугольники
Решение заданий второй части
15. (с развёрнутым свободным ответом)
В треугольнике АВС
МЕ параллелен стороне ВС, отрезок МК параллелен стороне АВ (точки Е и К лежат
на АВ и ВС соответственно). Докажите, что ЕК перпендикулярен ВМ.
Доказательство:
1) Четырёхугольник ВКМЕ – параллелограмм, т. к. МЕ || ВС, МК || АВ.
2) ВМ – диагональ параллелограмма, которая делит его угол пополам,
значит, ВКМЕ – ромб по второму признаку.
3) ЕК – диагональ ромба по свойству ромба,
что и требовалось доказать.
Слайд 57Треугольники
Решение заданий третьей части
Основную трудность при решении задач третьей (иногда и
работы, обычно, вызывают две главные причины:
для рационального решения задачи нужно знать некоторые методы и приёмы решения, которые, либо не рассматриваются при изучении планиметрии, либо тщательно не отрабатываются;
в задачах представлены не самые знакомые конфигурации и для того, чтобы применить известные факты, нужно уметь увидеть отдельные опорные подзадачи.
Слайд 58Треугольники
Решение заданий третьей части
(ГИА – 2008)
Найдите площадь остроугольного треугольника АВС,
, а .
B
Решение:
1) В остроугольном треугольнике АВС основание Н высоты ВН
лежит на стороне АС.
В прямоугольном треугольнике АВН:
2) Через точку М проведём прямую, параллельную прямой ВН и пересекающую сторону
АС в точке N.
Тогда по теореме Фалеса HN =NC.
Значит, отрезок MN является средней линией треугольника ВСН. Откуда имеем:
3) В прямоугольном треугольнике AMN: AN = 5,
Поскольку AN > АН, то HN = AN -AH и HN =1. Поскольку АС =AN + NC, HN = NC, то АС =6.
4)
Ответ: 12.
Слайд 59Треугольники
Решение заданий третьей части
2. (ГИА – 2008) Высоты треугольника пересекаются
Точка К – середина отрезка МН. Найдите площадь треугольника АКС, если известно,
что АВ = 12, СН = 6.
Решение:
По условию высоты треугольника АВС пересекаются, следовательно,
точка Н их пересечения расположена внутри этого треугольника.
Р 1) Пусть СР – высота, а BL – медиана - основания
перпендикуляров, проведённых из точек Н, К, М к прямой АС.
В прямоугольном треугольнике АРС:
2) В прямоугольном катеты равны:
А
В прямоугольном равнобедренном катеты равны:
(по двум углам), и (по свойству медиан треугольника).
Отсюда
4) Из теоремы Фалеса следует, что отрезок - средняя линия трапеции
5) Поскольку
Ответ: 22,5.