производных методом конечных разностей
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение дифференциальных уравнений в частных производных методом конечных разностей презентация
Содержание
- 1. Решение дифференциальных уравнений в частных производных методом конечных разностей
- 2. План Постановка задач для ДУЧП параболического типа
- 3. Исследование устойчивости методом гармонического анализа. Условия устойчивости
- 4. Дифференциальные уравнения в частных производных
- 5. Линейные ДУЧП второго порядка
- 6. Линейные ДУЧП второго порядка параболический тип
- 7. Примеры ДУЧП
- 8. Постановка задач для уравнений параболического типа Уравнение
- 9. Постановка задач для уравнений гиперболического типа
- 10. Постановка задач для уравнений гиперболического типа
- 11. Постановка задач для уравнений гиперболического типа
- 12. Постановка задач для уравнений эллиптического типа
- 13. Постановка задач для уравнений эллиптического типа
- 14. Постановка задач для уравнений эллиптического типа Третья краевая задача
- 15. Конечно-разностный метод (метод сеток): исходная область пространства
- 16. Равномерная (регулярная сетка) – сетка с постоянным
- 17. Разностные схемы для уравнений параболического типа Уравнение
- 18. Разностные схемы для уравнений параболического типа Неявная
- 19. Разностные схемы для уравнений параболического типа Система
- 20. Разностные схемы для уравнений параболического типа
- 21. Шаблоны разностных схем для уравнения теплопроводности
- 22. Постановка задач для уравнений гиперболического типа
- 23. Разностные схемы для уравнений гиперболического типа на
- 24. Разностные схемы для уравнений гиперболического типа на
- 25. Шаблоны разностных схем для волнового уравнения Шаблон явной схемы Шаблон неявной схемы
- 26. Разностные схемы для
- 27. Разностные схемы для
- 28. Разностные схемы для уравнений эллиптического типа
- 29. Шаблон разностной схемы
- 30. Метод простых итераций для
- 31. Итерационные методы решения ДУЧП эллиптического типа
- 32. Дифференциальная задача для ДУЧП Операторное представление дифференциальной
- 33. Операторное представление дифференциальной и конечно-разностной задач
- 34. Аппроксимация и порядок аппроксимации
- 35. Устойчивость
- 36. Устойчивость
- 37. Сходимость и порядок сходимости
- 38. Теорема эквивалентности
- 39. Консервативность Все ДУЧП выведены на основе физических
- 40. Корректность
- 41. Анализ устойчивости разностных схем для уравнения
- 42. Анализ устойчивости разностных схем для уравнения
- 43. Явная схема “против” потока
- 44. Анализ устойчивости схемы “против” потока
- 45. Анализ устойчивости схемы “против” потока
- 46. Критерий Куранта-Фридрихса-Леви Область зависимости точного решения
- 47. Анализ устойчивости схемы “по потоку” j
- 48. Интегро-интерполяционный метод стержень
- 49. Интегро-интерполяционный метод
- 50. Метод Неймана гармонического анализа устойчивости Неоднородное
- 51. Метод Неймана гармонического анализа устойчивости Гармоника:
- 52. Анализ устойчивости разностных схем для уравнения переноса
- 53. Анализ устойчивости разностных схем
- 54. Анализ устойчивости разностных схем для
- 55. уравнение переноса сетка
- 56. Анализ устойчивости разностных схем для уравнения переноса
- 57. Анализ устойчивости разностных схем для уравнения переноса
- 58. Условие устойчивости всегда не выполнено Схема
- 59. уравнение переноса сетка
- 60. Анализ устойчивости разностных схем для уравнения переноса
- 61. Анализ устойчивости разностных схем для уравнения переноса
- 62. Анализ устойчивости разностных схем для уравнения теплопроводности
- 63. Анализ устойчивости разностных схем для уравнения теплопроводности
- 64. Анализ устойчивости разностных схем для уравнения теплопроводности
- 65. Анализ устойчивости разностных схем для уравнения теплопроводности
- 66. Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Неявная схема
- 67. Анализ устойчивости разностных схем для уравнения теплопроводности
- 68. Анализ устойчивости разностных схем для волнового уравнения методом Неймана. Явная схема
- 69. Анализ устойчивости разностных схем для волнового уравнения
- 70. Анализ устойчивости разностных схем для волнового уравнения методом Неймана. Неявная схема
- 71. Анализ устойчивости разностных схем для волнового уравнения
- 72. Неявно-явные схемы с весами. Схема Кранка-Николсона явная
- 73. Неявно-явные схемы с весами. Схема Кранка-Николсона
- 74. Неявно-явные схемы с весами. Схема Кранка-Николсона неявно-явная
- 75. Схема с весами для уравнения теплопроводности
- 76. схема является абсолютно устойчивой точность схемы
- 77. Схема Кранка-Николсона для волнового уравнения
- 78. Многомерные задачи. Явные и неявные схемы двумерное
- 79. Явная схема гармоника для анализа устойчивости
- 80. Неявная схема шаблон неявной
- 81. Экономичность разностных схем. Методы расщепления Определение. Конечно-разностную
- 82. Методы расщепления полностью неявная схема
- 83. Методы расщепления ошибка расщепления
- 84. Методы расщепления
- 85. Методы расщепления
- 86. Метод расщепления по физическим процессам
- 87. Метод переменных направлений
- 88. Метод дробных шагов
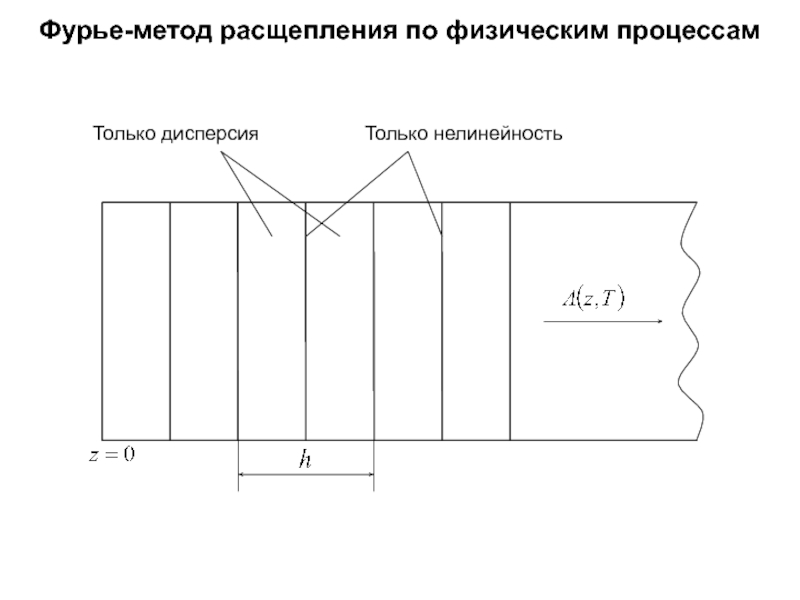
- 89. Фурье-метод расщепления по физическим процессам
- 90. Линейный шаг – применение преобразования Фурье
- 91. Нелинейный шаг – схема Кранка-Николсона
- 92. Фурье-метод расщепления по физическим процессам Только дисперсия Только нелинейность
План Постановка задач для ДУЧП параболического типа Постановка задач для ДУЧП гиперболического типа Постановка задач для ДУЧП эллиптического типа Конечно-разностные схемы. Основные определения: сеточная функция, временной слой, шаблон. Явные и неявные
Слайд 2План
Постановка задач для ДУЧП параболического типа
Постановка задач для ДУЧП гиперболического типа
Постановка
задач для ДУЧП эллиптического типа
Конечно-разностные схемы. Основные определения: сеточная функция, временной слой, шаблон. Явные и неявные схемы для ДУЧП параболического типа
Конечно-разностная аппроксимация задач для ДУЧП гиперболического типа
Конечно-разностная аппроксимация задач для ДУЧП эллиптического типа
Интегро-интерполяционный метод (метод конечных объемов)
Основные понятия для разностных схем: аппроксимация и порядок аппроксимации, сходимость и порядок сходимости, устойчивость, консервативность и корректность. Анализ порядка аппроксимации.
Конечно-разностные схемы. Основные определения: сеточная функция, временной слой, шаблон. Явные и неявные схемы для ДУЧП параболического типа
Конечно-разностная аппроксимация задач для ДУЧП гиперболического типа
Конечно-разностная аппроксимация задач для ДУЧП эллиптического типа
Интегро-интерполяционный метод (метод конечных объемов)
Основные понятия для разностных схем: аппроксимация и порядок аппроксимации, сходимость и порядок сходимости, устойчивость, консервативность и корректность. Анализ порядка аппроксимации.
Слайд 3Исследование устойчивости методом гармонического анализа. Условия устойчивости явных схем для основных
уравнений матфизики.
Неявно-явная конечно-разностная схема с весами. Схема Кранка-Николсона
Многомерные ДУЧП. Явные и неявные методы. Понятие об экономичных конечно-разностных схемах
Методы расщепления для многомерных уравнений параболического типа. Расщепление по пространственным переменным. Расщепление по физическим процессам.
Метод переменных направлений
Метод дробных шагов
Неявно-явная конечно-разностная схема с весами. Схема Кранка-Николсона
Многомерные ДУЧП. Явные и неявные методы. Понятие об экономичных конечно-разностных схемах
Методы расщепления для многомерных уравнений параболического типа. Расщепление по пространственным переменным. Расщепление по физическим процессам.
Метод переменных направлений
Метод дробных шагов
План
Слайд 6Линейные ДУЧП второго порядка
параболический тип
гиперболический тип
эллиптический тип
Линейные ДУЧП первого порядка
Слайд 8Постановка задач для уравнений параболического типа
Уравнение теплопроводности (диффузии)
Граничные условия первого рода
Начальное
условие
Граничные условия второго рода
Граничные условия третьего рода
Слайд 9Постановка задач для уравнений гиперболического типа
Волновое уравнение
Граничные условия первого рода
Начальные условия
Слайд 10Постановка задач для уравнений гиперболического типа
Волновое уравнение
Начальные условия
Граничные условия второго рода
Слайд 11Постановка задач для уравнений гиперболического типа
Волновое уравнение
Начальные условия
Граничные условия третьего рода
Слайд 13Постановка задач для уравнений эллиптического типа
Вторая краевая задача -
задача Неймана
Эквивалентное представление
граничного
условия
Слайд 15Конечно-разностный метод (метод сеток): исходная область пространства независимых переменных заменяется дискретным
множеством точек – сеткой,
а производные аппроксимируются на этой сетке разностными соотношениями.
В результате исходная задача для ДУЧП заменяется конечным числом алгебраических (разностных) уравнений, которые решаются.
Сетка – конечное множество точек (узлов сетки), принадлежащих области определения дифференциальной задачи, включая границу, на которой определяются начальные и граничные условия. Узлы, принадлежащие внутренней области, называются внутренними, узлы, принадлежащие границе, называются граничными
Шаг сетки – количественная характеристика плотности размещения узлов сетки. При стремлении шага сетки к нулю, сетка стремится заполнить область определения дифференциальной задачи.
Сеточная функция – функция, определенная в узлах сетки
Сеточное представление непрерывной функции – множество значений функции в узлах сетки
Разностная схема (задача) - совокупность разностных уравнений, аппроксимирующих ДУЧП во всех внутренних узлах сетки, а также начальные и краевые условия в граничных узлах сетки.
а производные аппроксимируются на этой сетке разностными соотношениями.
В результате исходная задача для ДУЧП заменяется конечным числом алгебраических (разностных) уравнений, которые решаются.
Сетка – конечное множество точек (узлов сетки), принадлежащих области определения дифференциальной задачи, включая границу, на которой определяются начальные и граничные условия. Узлы, принадлежащие внутренней области, называются внутренними, узлы, принадлежащие границе, называются граничными
Шаг сетки – количественная характеристика плотности размещения узлов сетки. При стремлении шага сетки к нулю, сетка стремится заполнить область определения дифференциальной задачи.
Сеточная функция – функция, определенная в узлах сетки
Сеточное представление непрерывной функции – множество значений функции в узлах сетки
Разностная схема (задача) - совокупность разностных уравнений, аппроксимирующих ДУЧП во всех внутренних узлах сетки, а также начальные и краевые условия в граничных узлах сетки.
Основные определения
Слайд 16Равномерная (регулярная сетка) – сетка с постоянным шагом по каждой независимой
переменной
Временной слой - множество всех узлов сетки, имеющих одну и ту же временную координату
Временной слой - множество всех узлов сетки, имеющих одну и ту же временную координату
Прямоугольная сетка
Пространственный и временной шаги сетки
Сеточное представление точного решения дифференциальной задачи
Дифференциальная задача с независимыми переменными x и t
Обычно x – пространственная координата, t – время
Прямоугольная область
Основные определения
- разностная схема;
- решение разностной схемы
Слайд 17Разностные схемы для уравнений параболического типа
Уравнение теплопроводности (диффузии)
Аппроксимация производной по времени
Явная
аппроксимация пространственной производной (используются известные значения на k-м временном слое)
Явная разностная схема
для первой начально-краевой
задачи
Явная разностная схема
для первой начально-краевой
задачи
Одно неизвестное значение может быть явно рассчитано через известные
Схема называется явной, если аппроксимирующее уравнение содержит только одно неизвестное значение функции на (k+1)-м слое, которое может быть выражено явно через известные значения на k-м слое.
Слайд 18Разностные схемы для уравнений параболического типа
Неявная разностная схема
для первой начально-краевой
задачи
Неизвестные значения
Неявная
аппроксимация пространственной производной (используются неизвестные значения на (k+1)-м временном слое)
Схема называется неявной, если оператор аппроксимируется с использованием нескольких неизвестных значений функции на (k+1)-м слое.
Слайд 19Разностные схемы для уравнений параболического типа
Система линейных алгебраических уравнений,
полученная по
неявной разностной схеме,
может быть решена методом прогонки
может быть решена методом прогонки
где
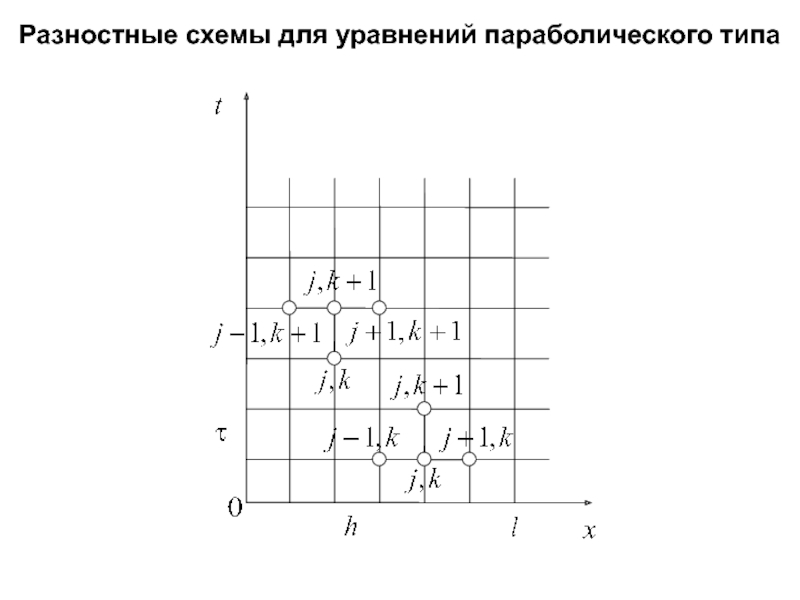
Слайд 21Шаблоны разностных схем
для уравнения теплопроводности
Шаблон явной схемы Шаблон неявной схемы
Шаблон
– совокупность узлов сетки, значения в которых используются при аппроксимации дифференциального оператора.
Шаблон, содержащий p узлов называется p-точечным.
Шаблон, содержащий p узлов называется p-точечным.
Слайд 22Постановка задач для уравнений гиперболического типа
Волновое уравнение
Граничные условия первого рода
Начальные условия
Слайд 23Разностные схемы для уравнений гиперболического типа на примере волнового уравнения
Явная схема
для волнового уравнения
Неявная схема для волнового уравнения
Слайд 24Разностные схемы для уравнений гиперболического типа на примере волнового уравнения
Явная схема
для волнового уравнения
Неявная схема для волнового уравнения
Слайд 26
Разностные схемы для уравнений гиперболического типа на примере волнового уравнения
Начальные условия
Аппроксимация
начальных
условий
Слайд 27
Разностные схемы для уравнений гиперболического типа на примере волнового уравнения
Начальные условия
Аппроксимация
начальных
условий
со вторым порядком
аппроксимации
по времени
со вторым порядком
аппроксимации
по времени
Слайд 28Разностные схемы для уравнений эллиптического типа
Задача Дирихле
Сетка для
прямоугольной
области
Разностная схема
для внутренних точек
Слайд 30
Метод простых итераций для ДУЧП эллиптического типа
Итерации сходятся при
Сходимость может быть медленной
Итерационный процесс Либмана
Слайд 31Итерационные методы решения
ДУЧП эллиптического типа
Метод Зейделя
Метод релаксации
метод нижней релаксации
метод верхней
релаксации
Слайд 32Дифференциальная задача для ДУЧП
Операторное представление дифференциальной задачи
Все, связанное с неизвестной функцией
U, помещено в оператор L:
Область пространства независимых переменных
Дифференциальный оператор
Тип дифференциальной задачи
Область пространства независимых переменных
Дифференциальный оператор
Тип дифференциальной задачи
Все, связанное с конкретизацией задачи, помещено в функцию f :
Правая часть
Начальные условия
Граничные условия
Пример: начально-краевая задача для уравнения переноса
Слайд 33Операторное представление
дифференциальной и конечно-разностной задач
дифференциальная задача для ДУЧП
дифференциальный оператор
неизвестная искомая
функция
входные данные
дифференциальная задача в узлах сетки
конечно-разностная схема на точном (неизвестном) решении
конечно-разностная схема
сеточная функция, которую мы находим в процессе решения по конечно-разностной схеме
входные данные
дифференциальная задача в узлах сетки
конечно-разностная схема на точном (неизвестном) решении
конечно-разностная схема
сеточная функция, которую мы находим в процессе решения по конечно-разностной схеме
Слайд 39Консервативность
Все ДУЧП выведены на основе физических законов сохранения какой-либо субстанции (массы,
энергии, импульса и т.п.). Заменяя дифференциальную задачу конечно-разностной схемой, можно нарушить эти законы сохранения.
Определение. Конечно-разностная схема консервативна, если для нее выполняются законы сохранения, на основе которых поставлена дифференциальная задача.
В противном случае конечно-разностная схема является неконсервативной, т.е. решение, полученное на ее основе, не соответствует решению дифференциальной задачи - решается другая задача. Поэтому неконсервативными схемами пользоваться не рекомендуется.
Определение. Конечно-разностная схема консервативна, если для нее выполняются законы сохранения, на основе которых поставлена дифференциальная задача.
В противном случае конечно-разностная схема является неконсервативной, т.е. решение, полученное на ее основе, не соответствует решению дифференциальной задачи - решается другая задача. Поэтому неконсервативными схемами пользоваться не рекомендуется.
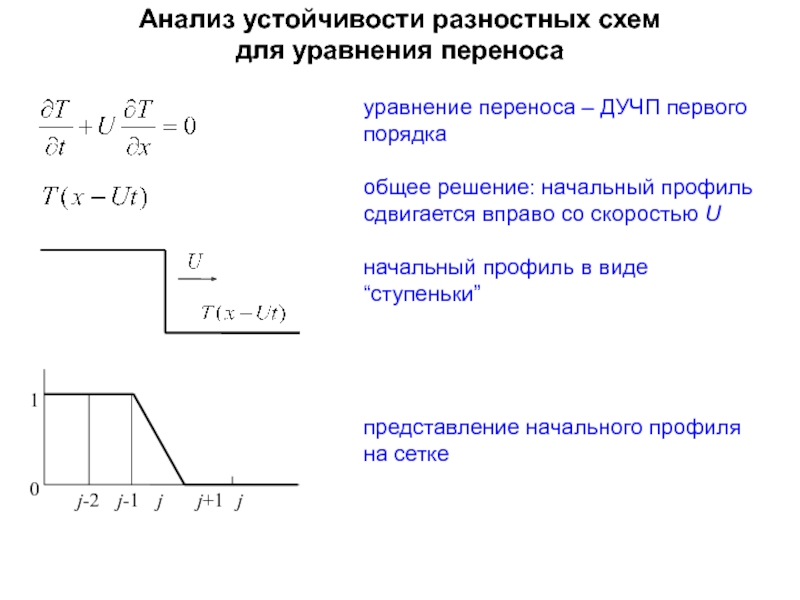
Слайд 41Анализ устойчивости разностных схем
для уравнения переноса
1
j-2 j-1 j j+1 j
0
уравнение переноса – ДУЧП
первого порядка
общее решение: начальный профиль сдвигается вправо со скоростью U
начальный профиль в виде “ступеньки”
представление начального профиля на сетке
общее решение: начальный профиль сдвигается вправо со скоростью U
начальный профиль в виде “ступеньки”
представление начального профиля на сетке
Слайд 42Анализ устойчивости разностных схем
для уравнения переноса
уравнение переноса
сетка
аппроксимация производной по времени
варианты
аппроксимации
пространственной производной
пространственной производной
Слайд 45
Анализ устойчивости схемы “против” потока
условие устойчивости схемы “против” потока
скорость распространения возмущения
в конечно-разностной схеме
другая формулировка условия устойчивости:
скорость распространения схемного возмущения должна быть не меньше скорости распространения возмущения, определяемого физикой процессов
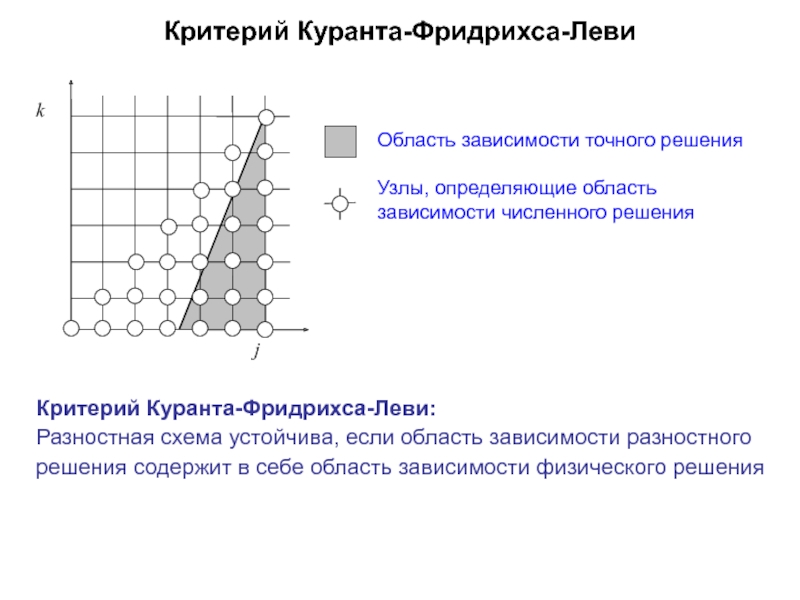
Слайд 46Критерий Куранта-Фридрихса-Леви
Область зависимости точного решения
Узлы, определяющие область зависимости численного решения
Критерий Куранта-Фридрихса-Леви:
Разностная схема устойчива, если область зависимости разностного решения содержит в себе область зависимости физического решения
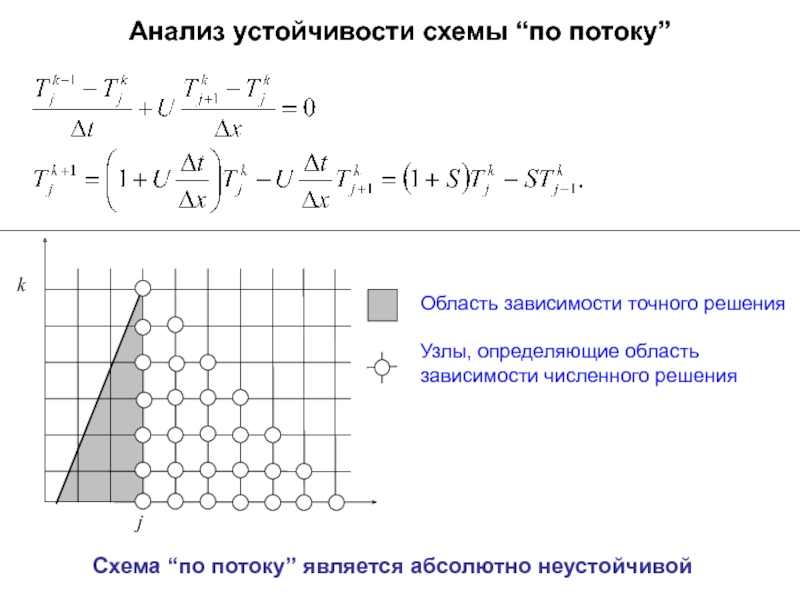
Слайд 47Анализ устойчивости схемы “по потоку”
j
k
Область зависимости точного решения
Узлы, определяющие область зависимости
численного решения
Cхема “по потоку” является абсолютно неустойчивой
Слайд 50Метод Неймана гармонического анализа устойчивости
Неоднородное уравнение:
уравнение переноса с источником Q
точное
решение
возмущение точного решения
подстановка решения с возмущением в уравнение
Однородное уравнение
для возмущения
При анализе устойчивости рассматривают
однородные уравнения для возмущений
Слайд 51Метод Неймана гармонического анализа устойчивости
Гармоника:
.
Конечно-разностный аналог гармоники на сетке:
Необходимое условие устойчивости – отсутствие возрастания
малых возмущений для всех собственных чисел:
Слайд 52Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Схема “против
потока”
уравнение переноса
сетка
схема “против потока”
гармоника
Слайд 53
Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Схема “против
потока”
схема “против потока”
гармоника
Слайд 54
Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Схема “против
потока”
условие устойчивости схемы “против потока”
Слайд 55уравнение переноса
сетка
схема “по потоку”
гармоника
Анализ устойчивости разностных схем для уравнения переноса методом
Неймана. Схема “по потоку”
Слайд 56Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Схема “по
потоку”
схема “по потоку”
гармоника
Слайд 57Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Схема “по
потоку”
схема “по потоку”
гармоника
Слайд 58
Условие устойчивости всегда не выполнено
Схема “по потоку” абсолютно неустойчивая
Анализ устойчивости разностных
схем для уравнения переноса методом Неймана. Схема “по потоку”
Слайд 59уравнение переноса
сетка
неявная схема “против потока”
гармоника
Анализ устойчивости разностных схем для уравнения переноса
методом Неймана. Неявная схема
Слайд 60Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Неявная схема
неявная
схема
“против потока”
гармоника
“против потока”
гармоника
Слайд 61Анализ устойчивости разностных схем для уравнения переноса методом Неймана. Неявная схема
неявная
схема
“против потока”
гармоника
условие
устойчивости
всегда выполнено
“против потока”
гармоника
условие
устойчивости
всегда выполнено
Слайд 62Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Явная схема
Слайд 63Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Явная схема
Слайд 64Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Явная схема
Условие
устойчивости
явной
схемы
Слайд 65Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Неявная схема
Слайд 66Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Неявная схема
Слайд 67Анализ устойчивости разностных схем для уравнения теплопроводности методом Неймана. Неявная схема
Неявная
схема
абсолютно
устойчива
Слайд 69Анализ устойчивости разностных схем для волнового уравнения методом Неймана. Явная схема
Условие
устойчивости явной схемы
Правое неравенство выполнено всегда
Слайд 71Анализ устойчивости разностных схем для волнового уравнения методом Неймана. Неявная схема
Неявная
схема абсолютно устойчива
Слайд 72Неявно-явные схемы с весами. Схема Кранка-Николсона
явная схема
неявная схема
ДУЧП параболического
типа
(эволюционное уравнение)
(эволюционное уравнение)
оператор, содержащий
пространственные производные
неявно-явная
схема с весами
веса
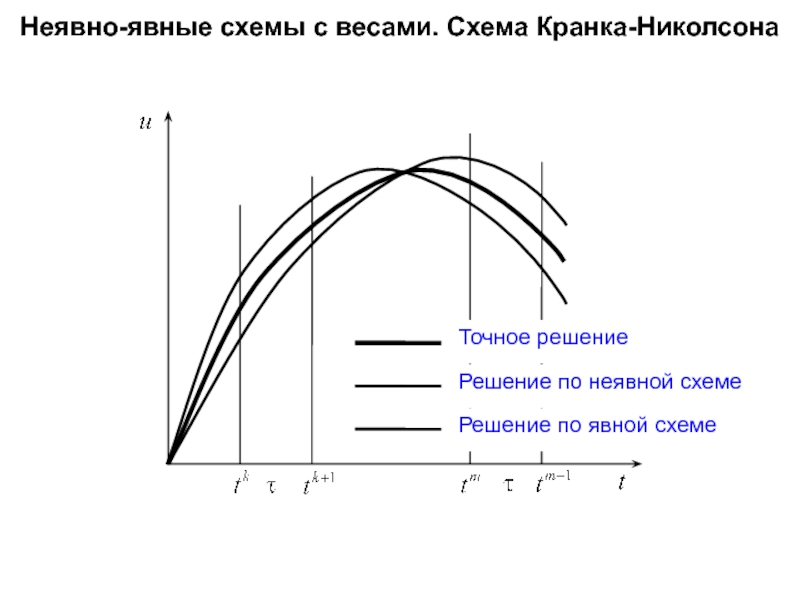
Слайд 73Неявно-явные схемы с весами. Схема Кранка-Николсона
Точное решение
Решение по неявной схеме
Решение по
явной схеме
Слайд 74Неявно-явные схемы с весами. Схема Кранка-Николсона
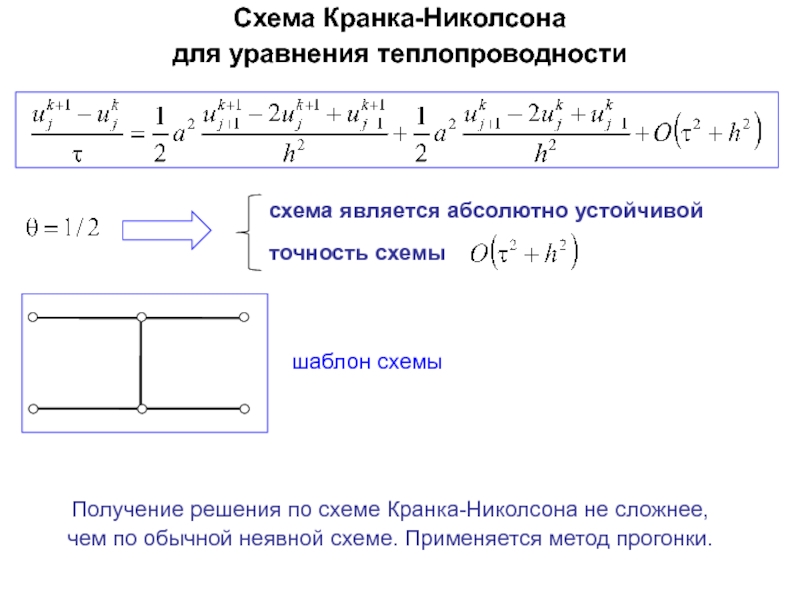
неявно-явная
схема с весами
Схема
Кранка-
Николсона
Слайд 75Схема с весами для уравнения теплопроводности
условие устойчивости
абсолютная устойчивость
условная устойчивость
точность схемы
Слайд 76схема является абсолютно устойчивой
точность схемы
Схема Кранка-Николсона
для уравнения теплопроводности
Получение решения по
схеме Кранка-Николсона не сложнее,
чем по обычной неявной схеме. Применяется метод прогонки.
чем по обычной неявной схеме. Применяется метод прогонки.
шаблон схемы
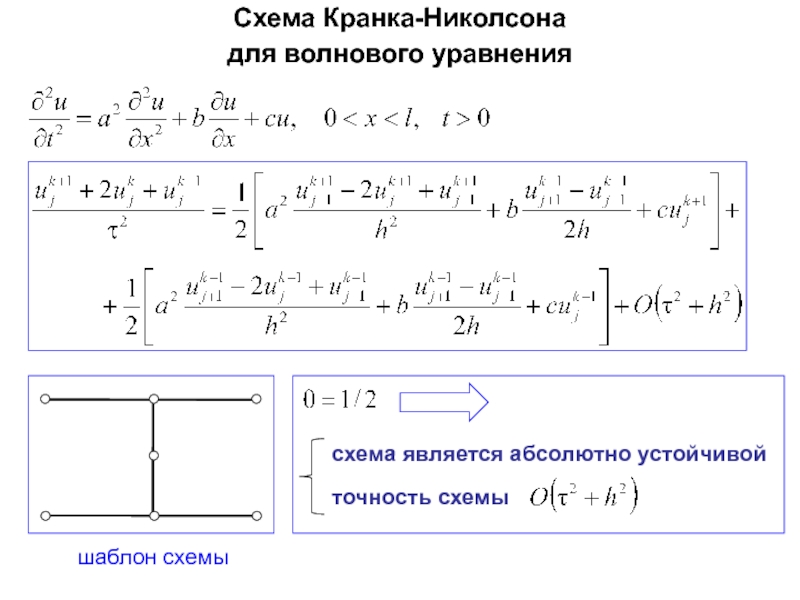
Слайд 77Схема Кранка-Николсона
для волнового уравнения
шаблон схемы
схема является абсолютно устойчивой
точность схемы
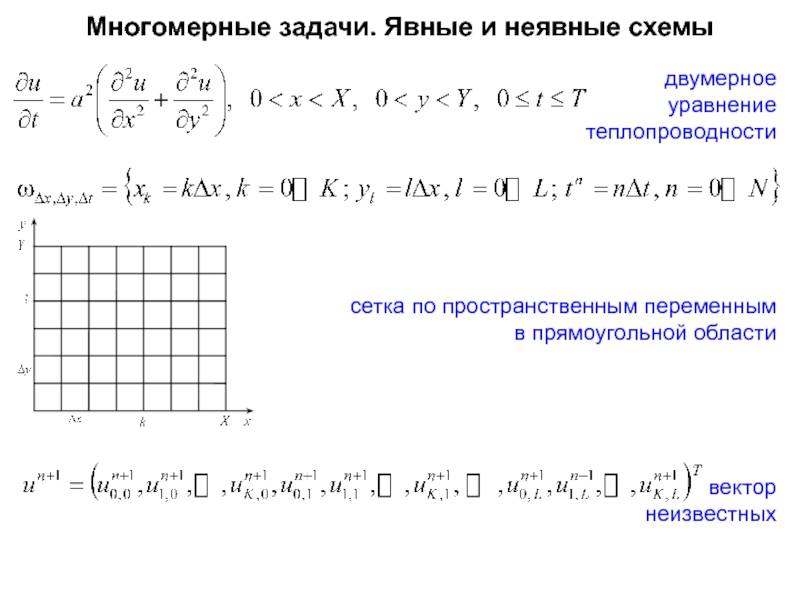
Слайд 78Многомерные задачи. Явные и неявные схемы
двумерное
уравнение
теплопроводности
сетка по пространственным переменным
в
прямоугольной области
вектор
неизвестных
Слайд 79Явная схема
гармоника для
анализа устойчивости
условие устойчивости
шаблон
явной схемы
явная схема,
операторное представление
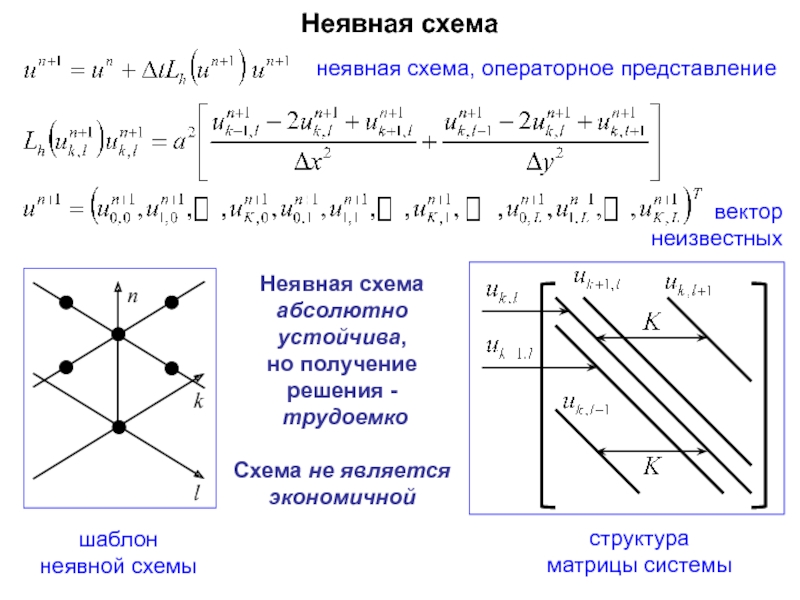
Слайд 80Неявная схема
шаблон
неявной схемы
неявная схема, операторное представление
структура
матрицы системы
Неявная схема абсолютно устойчива,
но получение решения -
трудоемко
Схема не является экономичной
вектор
неизвестных
Слайд 81Экономичность разностных схем. Методы расщепления
Определение. Конечно-разностную схему будем называть экономичной, если
число длинных операций (типа умножения) пропорционально числу узлов сетки.
Явные схемы для многомерных задач –
экономичные, но условно устойчивые
Неявные схемы для многомерных задач -
абсолютно устойчивые, но не экономичные
Для обеспечения экономичности неявных схем применяют
методы расщепления.
В методах расщепления неэкономичный оператор
переписывают в виде произведения более простых
экономичных операторов, т.е. факторизуют.
Слайд 84Методы расщепления
- результат с предыдущего временном слоя
оба этапа могут быть реализованы
методом прогонки,
что обеспечивает
экономичность
метода расщепления
что обеспечивает
экономичность
метода расщепления
исходная схема
На первом этапе - метод прогонки для каждого отсчета по переменной y (для всех l), на втором - для каждого отсчета по x (для всех k)
Слайд 85Методы расщепления
- результат с предыдущего временном слоя
исходная схема
На первом этапе -
метод прогонки для каждого отсчета по переменной y (для всех l), на втором - для каждого отсчета по x (для всех k)
Слайд 86Метод расщепления по физическим процессам
Метод реализуется за M этапов
Расщепление
Ошибка имеет
второй порядок по шагу по времени
