- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение дифференциальных уравнений в частных производных презентация
Содержание
- 1. Решение дифференциальных уравнений в частных производных
- 2. Классификация дифференциальных уравнений обыкновенные дифференциальные уравнения, содержащие
- 3. Численные методы решения дифференциальных уравнений в
- 4. Классификация дифференциальных уравнений в частных производных В
- 5. Классификация дифференциальных уравнений в частных производных
- 6. Примеры дифференциальных уравнений в частных производных уравнение
- 7. Примеры дифференциальных уравнений в частных производных уравнение
- 8. Дифференциальные уравнений в частных производных Эллиптические уравнения
- 9. Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток Граничные условия
- 10. Задача 1. Решение задачи Дирихле для уравнения
- 11. Задача 1. Решение задачи Дирихле для уравнения
- 12. Задача 1. Решение задачи Дирихле для уравнения
- 13. Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток Шаблон типа «крест»
- 14. Задача 1. Решение задачи Дирихле для уравнения
- 15. Задача 1. Решение задачи Дирихле для уравнения
- 16. Задача 1. Решение задачи Дирихле для уравнения
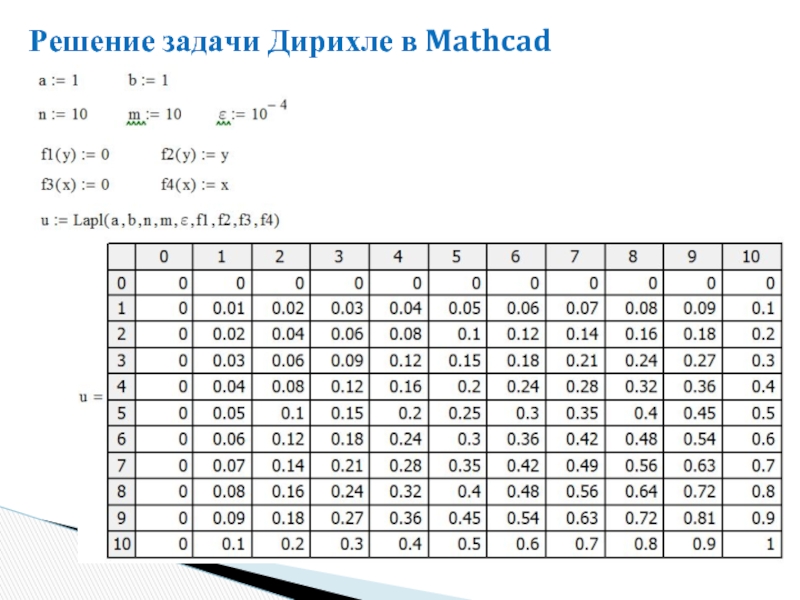
- 17. Решение задачи Дирихле в Mathcad . . .
- 18. Решение задачи Дирихле в Mathcad
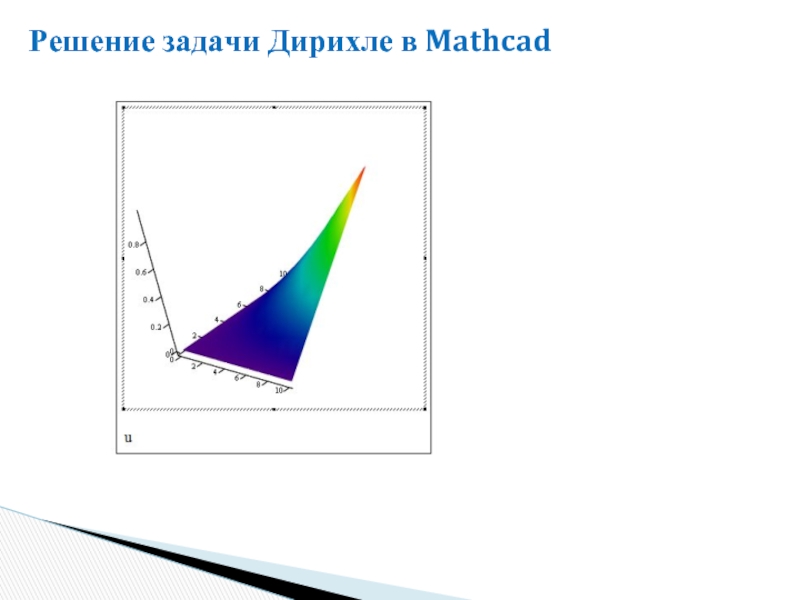
- 19. Решение задачи Дирихле в Mathcad
- 20. Решение задачи Дирихле в Mathcad
- 21. Задача 2. Решение уравнения гиперболического типа методом сеток граничные условия начальные условия Замена переменной
- 22. Задача 2. Решение уравнения гиперболического типа методом
- 23. Конечно-разностный вид уравнения Задача 2. Решение уравнения гиперболического типа методом сеток
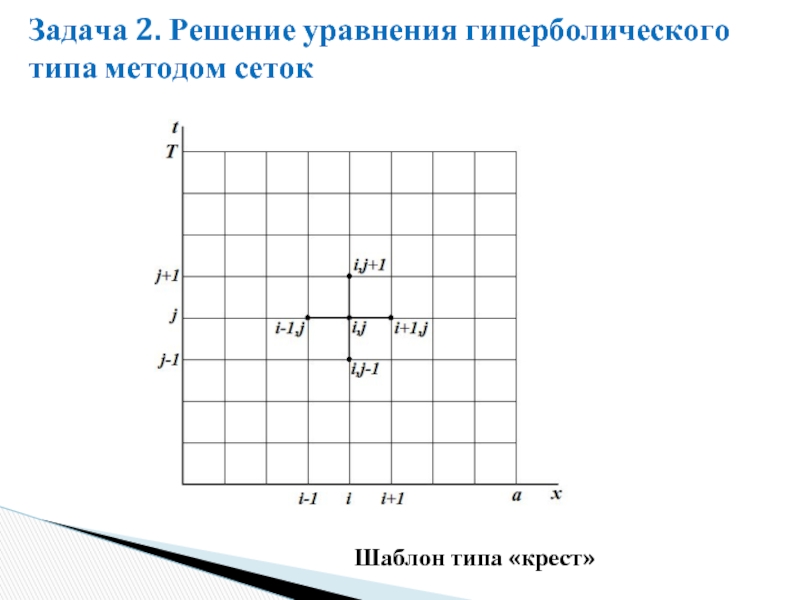
- 24. Задача 2. Решение уравнения гиперболического типа методом сеток Шаблон типа «крест»
- 25. Задача 2. Решение уравнения гиперболического типа методом сеток
- 26. Задача 2. Решение уравнения гиперболического типа методом
- 27. Алгоритм решения задачи 1. Задание шага сетки
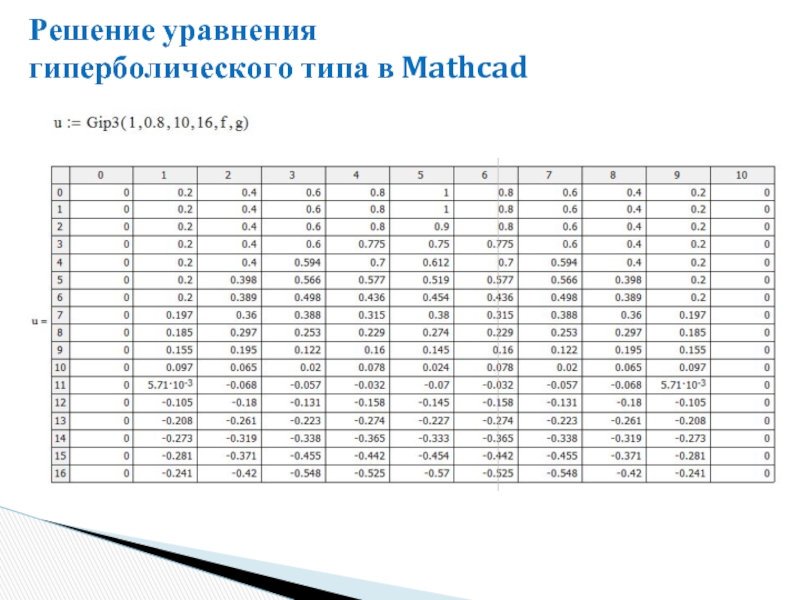
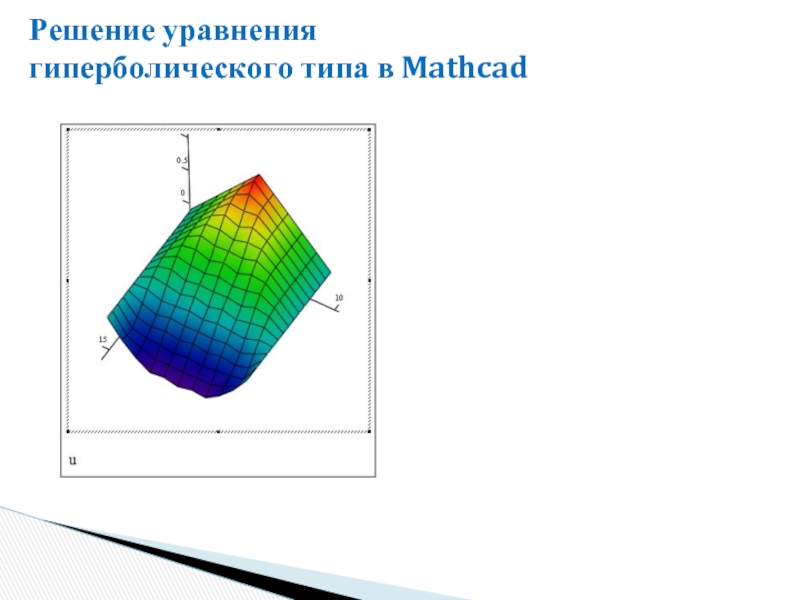
- 28. Решение уравнения гиперболического типа в Mathcad
- 29. Решение уравнения гиперболического типа в Mathcad
- 30. Решение уравнения гиперболического типа в Mathcad
- 31. Решение уравнения гиперболического типа в Mathcad
- 32. Задача 3. Решение уравнения параболического типа методом сеток граничные условия начальные условия Замена переменной
- 33. Построение сетки h ‒ шаг сетки
- 34. Конечно-разностный вид уравнения Задача 3. Решение уравнения параболического типа методом сеток погрешность аппроксимации
- 35. Задача 3. Решение уравнения параболического типа методом
- 36. Задача 3. Решение уравнения параболического типа методом сеток Система уравнений
- 37. Алгоритм решения задачи 1. Задание шага 2.
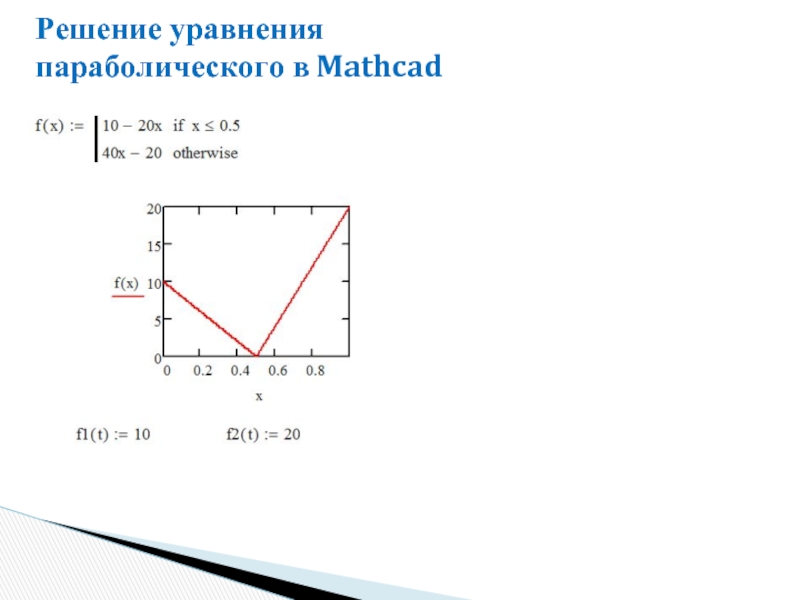
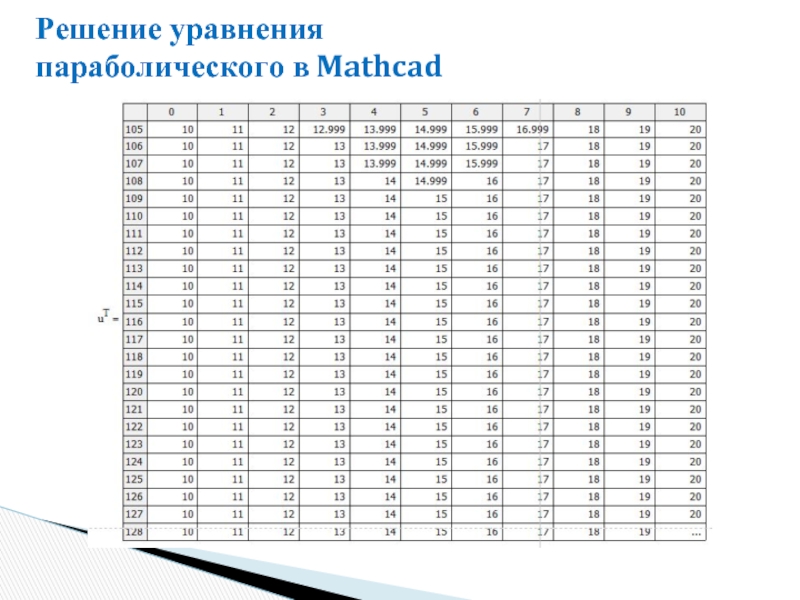
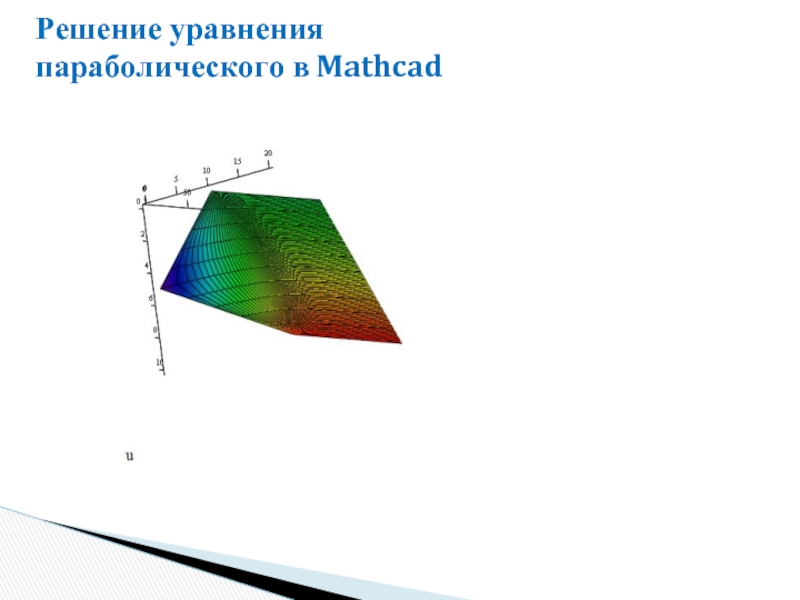
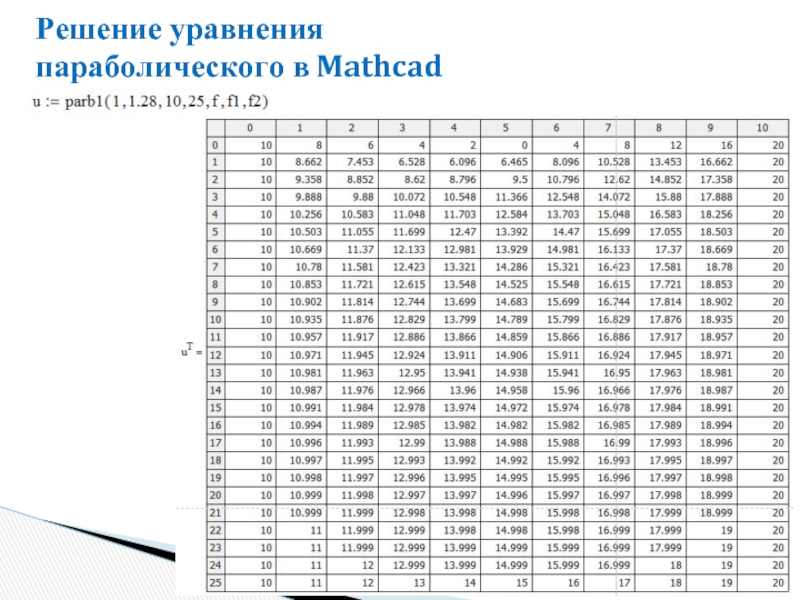
- 38. Решение уравнения параболического в Mathcad
- 39. Решение уравнения параболического в Mathcad
- 40. Решение уравнения параболического в Mathcad
- 41. Решение уравнения параболического в Mathcad
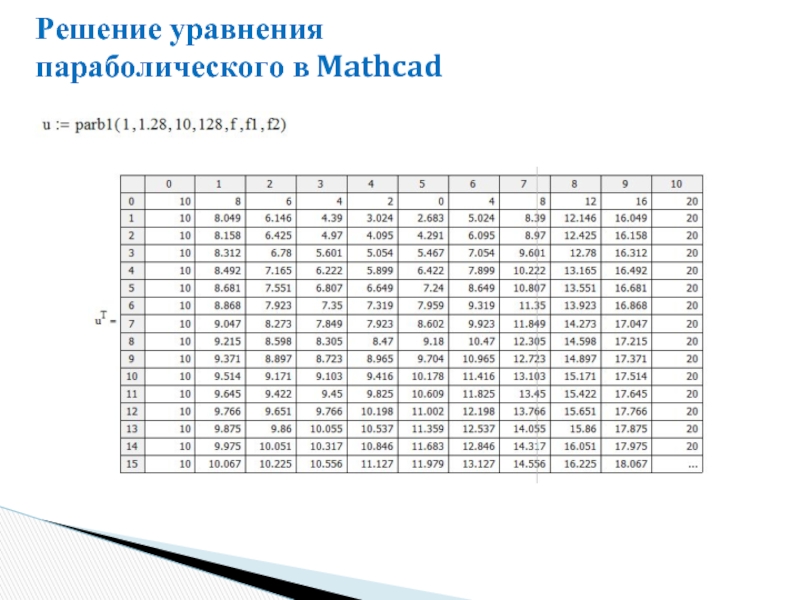
- 42. Решение уравнения параболического в Mathcad
- 43. Решение уравнения параболического в Mathcad
- 44. Решение уравнения параболического в Mathcad
- 45. Решение уравнения параболического в Mathcad
- 46. Конечно-разностный вид уравнения (явная схема) Задача 3. Решение уравнения параболического типа методом сеток погрешность аппроксимации
- 47. Задача 3. Решение уравнения параболического типа методом
- 48. Задание Написать программу решения задачи Дирихле для
- 49. Вопросы Перечислите численные методы, используемые при решении
- 50. Вопросы Запишите уравнение теплопроводности в конечно-разностной форме
- 51. Благодарю за внимание!
Слайд 2Классификация дифференциальных уравнений
обыкновенные дифференциальные уравнения, содержащие одну независимую переменную и производные
дифференциальные уравнения в частных производных, содержащие несколько независимых переменных и производные по ним.
В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных:
Слайд 3Численные методы решения
дифференциальных уравнений в частных производных
метод конечных разностей (МКР);
метод
метод конечных элементов (МКЭ).
Слайд 4Классификация дифференциальных уравнений в частных производных
В зависимости от математической природы ДУ:
эллиптические;
параболические;
гиперболические.
В
уравнение диффузии;
уравнение теплопроводности;
волновое уравнение.
Слайд 5Классификация дифференциальных уравнений в частных производных
– параболическое уравнение;
– гиперболическое уравнение.
С математической точки зрения дифференциальные уравнения второго порядка в частных производных с двумя независимыми переменными
классифицируются в зависимости от характера функций A, B и С.
Слайд 6Примеры дифференциальных уравнений
в частных производных
уравнение Лапласа
одномерное волновое уравнение
уравнение теплопроводности
гиперболическое
эллиптическое уравнение
параболическое уравнение
Слайд 7Примеры дифференциальных уравнений
в частных производных
уравнение Гельмгольца (Блохинцева)
Звуковые поля в среде, движущейся с дозвуковой скоростью.
– параболическое уравнение;
– гиперболическое уравнение.
Решения таких уравнений рассматриваются в газодинамике больших скоростей, когда в поле течения появляются скачки уплотнения и ударные волны, в частности, при исследовании распространения звукового удара от сверхзвукового самолета.
Слайд 8Дифференциальные уравнений
в частных производных
Эллиптические уравнения описывают установившиеся (стационарные) процессы.
Задача ставится
Параболическими и гиперболическими уравнениями описываются эволюционные процессы (процессы «распространения»).
В таких задачах на одной части границы ставятся начальные условия, на другой – граничные; возможны также открытые области, в которые «распространяется решение».
Дополнительные условия для дифференциальных уравнений в частных производных:
граничные условия;
начальные условия;
комбинация граничных и начальных условий.
Слайд 10Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток
Построение сетки
шаг сетки
координаты узлов сетки
значение функции
Слайд 11Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток
Аппроксимация частных
Конечно-разностное уравнение Лапласа
Найти ошибку в записи к/р уравнения Лапласа
Слайд 12Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток
Система линейных
Набор узлов, используемых для аппроксимации уравнения в точке, называется шаблоном.
Слайд 14Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток
Итерационный метод
Условие окончания итерационного процесса
Итерационный процесс сходится медленно
Более надежный критерий
Слайд 15Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток
Погрешность приближенного
погрешность аппроксимации дифференциального уравнения разностным уравнением;
погрешность, возникающая в результате приближенного решения системы разностных уравнений.
Свойство используемой разностной схемы:
свойство устойчивости;
свойство сходимости.
Устойчивость схемы означает, что малые изменения в начальных данных приводят к малым изменениям решения разностной задачи.
Сходимость схемы означает, что при стремлении шага сетки к нулю решение разностной задачи стремится к решению исходной задачи.
Слайд 16Задача 1. Решение задачи Дирихле для уравнения Лапласа методом сеток
Алгоритм решения
1. Задание шага
2. Задание граничных условий
3. Задание начального приближения
4. Уточнение решения
5. Проверка условия окончания итерационного процесса
Слайд 21Задача 2. Решение уравнения гиперболического типа методом сеток
граничные условия
начальные условия
Замена переменной
Слайд 22Задача 2. Решение уравнения гиперболического типа методом сеток
Построение сетки
h ‒
координаты узлов сетки
значение функции
τ ‒ шаг сетки в направлении t.
Слайд 23Конечно-разностный вид уравнения
Задача 2. Решение уравнения гиперболического типа методом сеток
Слайд 26Задача 2. Решение уравнения гиперболического типа методом сеток
Условие Куранта означает, что
Слайд 27Алгоритм решения задачи
1. Задание шага сетки
Задача 2. Решение уравнения гиперболического типа
2. Вычисление решения на нулевом временном слое
3. Вычисление решения на первом временном слое
4. Вычисление решения на каждом следующем слое
вычисляются из граничных условий.
вычисляются из граничных условий.
Слайд 32Задача 3. Решение уравнения параболического типа методом сеток
граничные условия
начальные условия
Замена переменной
Слайд 33Построение сетки
h ‒ шаг сетки в направлении x;
координаты узлов
значение функции
τ ‒ шаг сетки в направлении t.
Задача 3. Решение уравнения параболического типа методом сеток
Слайд 34Конечно-разностный вид уравнения
Задача 3. Решение уравнения параболического типа методом сеток
погрешность аппроксимации
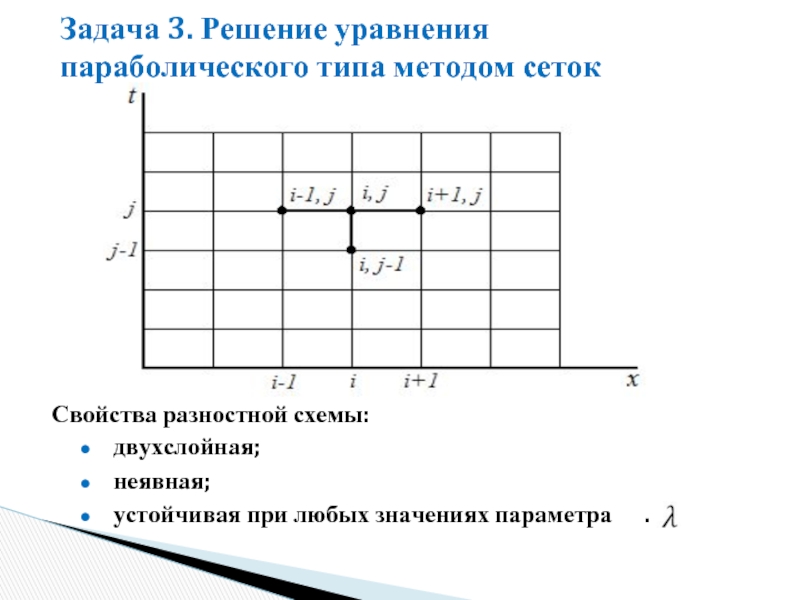
Слайд 35Задача 3. Решение уравнения параболического типа методом сеток
двухслойная;
неявная;
устойчивая при любых значениях
Свойства разностной схемы:
Слайд 37Алгоритм решения задачи
1. Задание шага
2. Вычисление решения на нулевом временном слое
3.
(решение трехдиагональной системы уравнений)
Задача 3. Решение уравнения параболического типа методом сеток
Слайд 46Конечно-разностный вид уравнения (явная схема)
Задача 3. Решение уравнения параболического типа методом
погрешность аппроксимации
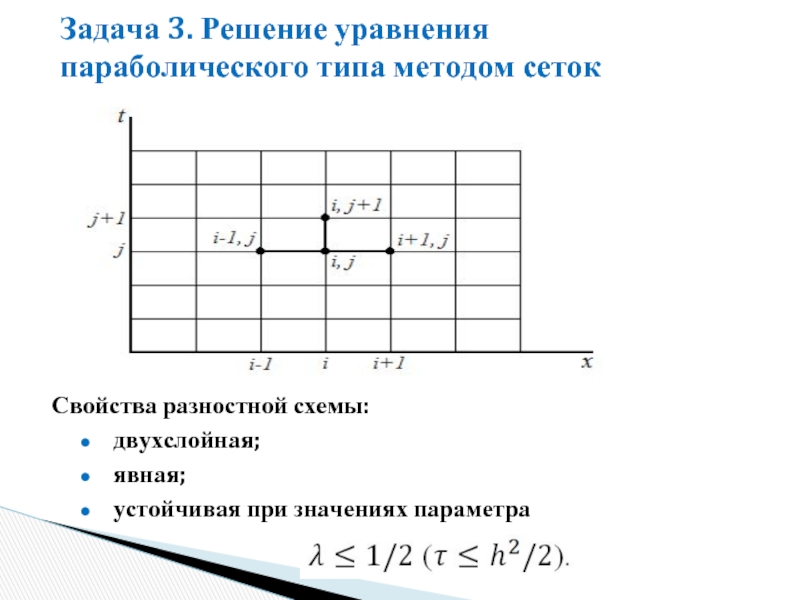
Слайд 47Задача 3. Решение уравнения параболического типа методом сеток
двухслойная;
явная;
устойчивая при значениях параметра
Свойства
Слайд 48Задание
Написать программу решения задачи Дирихле для уравнения Лапласа методом сеток (Mathcad).
Написать
Написать программу решения уравнения параболического типа методом сеток с использованием неявной схемы (Mathcad).
Написать программу решения уравнения параболического типа методом сеток с использованием явной схемы (Mathcad).
Варианты заданий
Плис А.И., Сливина. Лабораторный практикум по высшей математике (лабораторные работы №42–44).
Слайд 49Вопросы
Перечислите численные методы, используемые при решении дифференциальных уравнений в частных производных.
Классификация
Классификация дифференциальных уравнений в частных производных в зависимости от физического смысла решаемых с их помощью задач.
Какие процессы описывают эллиптические уравнения?
Какие процессы описываются параболическими и гиперболическими уравнениями?
Запишите уравнение Лапласа в конечно-разностной форме.
Запишите волновое уравнение в конечно-разностной форме.
Слайд 50Вопросы
Запишите уравнение теплопроводности в конечно-разностной форме (явная схема).
Запишите уравнение теплопроводности в
Основные свойства разностных схем.
Преимущества и недостатки явной схемы.
Преимущества и недостатки неявной схемы.