- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение алгебраических и трансцендентных уравнений презентация
Содержание
- 1. Решение алгебраических и трансцендентных уравнений
- 2. Решить уравнение – это значит: установить,
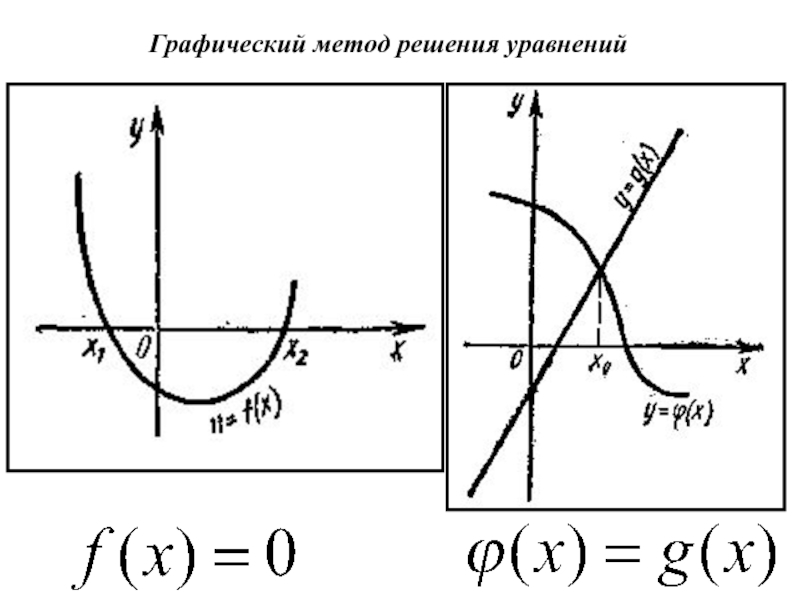
- 3. Графический метод решения уравнений
- 4. Пример: Решить графически уравнение х3 -
- 5. Задача численного нахождения корней уравнения
- 6. Отделение корней Корень уравнения f(х) =
- 7. Аналитический метод отделения корней 1) Если
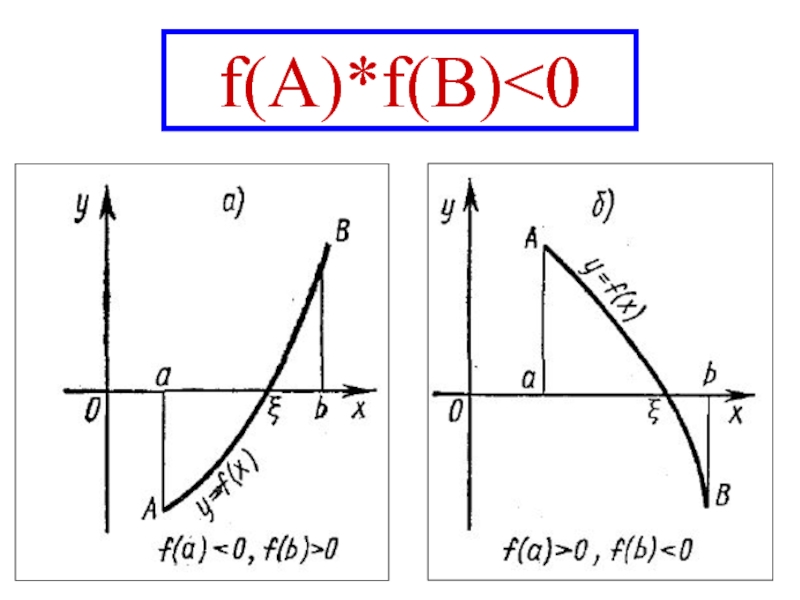
- 8. f(A)*f(B)
- 9. Метод половинного деления
- 14. Алгоритм данного метода: 1.Определить начальные данные (a,
- 15. Методом половинного деления уточнить корень уравнения x4
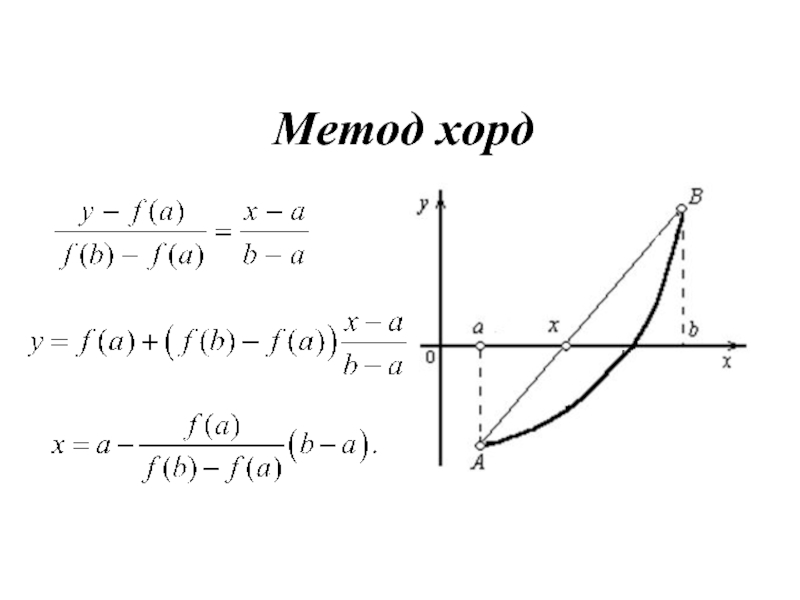
- 16. Метод хорд Применяется в том случае,
- 17. Метод хорд
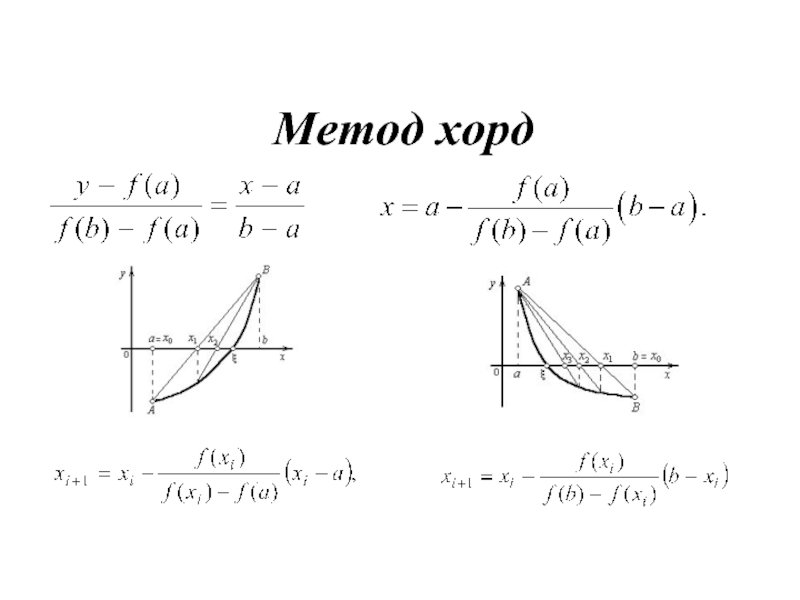
- 18. Метод хорд
- 19. Найти положительный корень уравнения (методом хорд)
- 20. Метод Ньютона (касательной) В качестве исходной
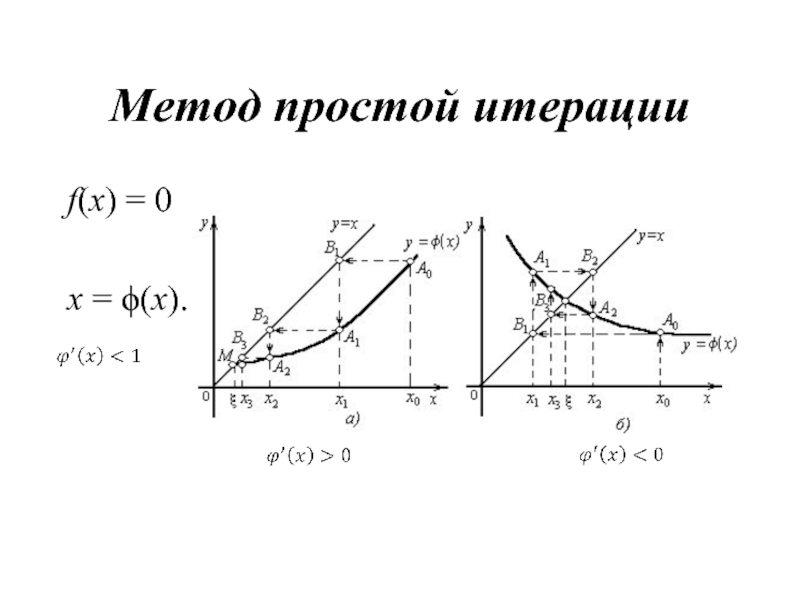
- 21. Метод простой итерации f(х) = 0 x = ϕ(x).
- 22. Решить уравнение x3 – x – 1 = 0, на интервале 1
Слайд 2 Решить уравнение – это значит:
установить, имеет ли
оно корни
сколько корней
и найти
значение корней с
заданной точностью
заданной точностью
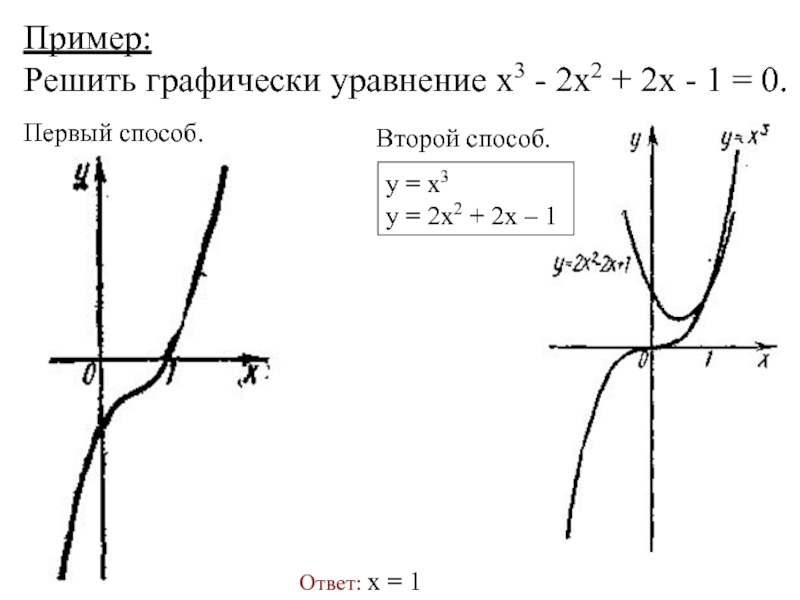
Слайд 4Пример:
Решить графически уравнение х3 - 2x2 + 2х - 1
= 0.
Первый способ.
Второй способ.
у = х3
у = 2x2 + 2х – 1
Ответ: х = 1
Слайд 5Задача численного нахождения
корней уравнения
состоит из двух этапов:
отделение корней
уточнение корней
Слайд 6Отделение корней
Корень уравнения f(х) = 0 считается
отделенным на отрезке
[a,b], если на этом
отрезке уравнение f(х) = 0 не имеет
других корней
отрезке уравнение f(х) = 0 не имеет
других корней
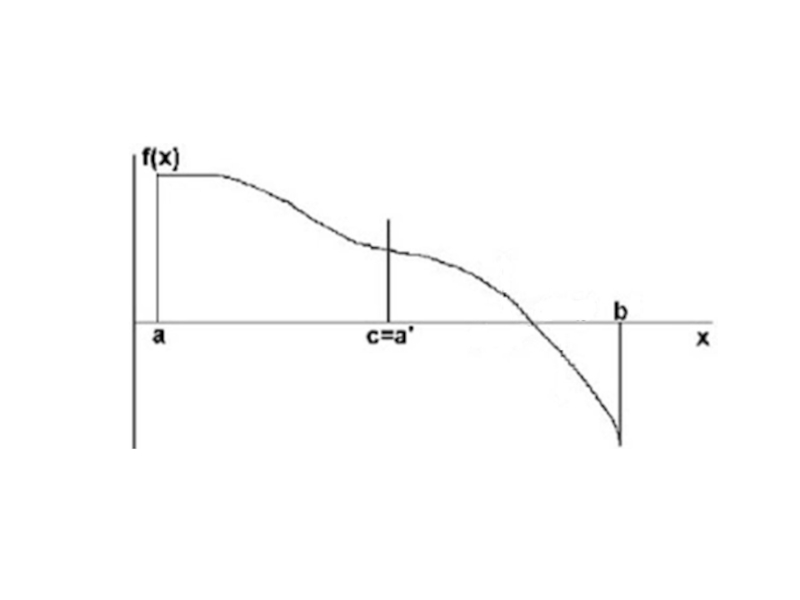
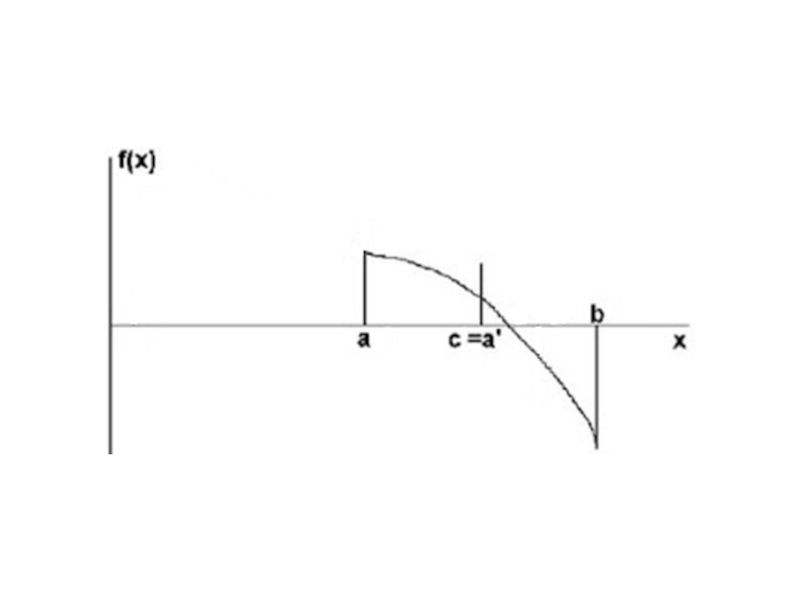
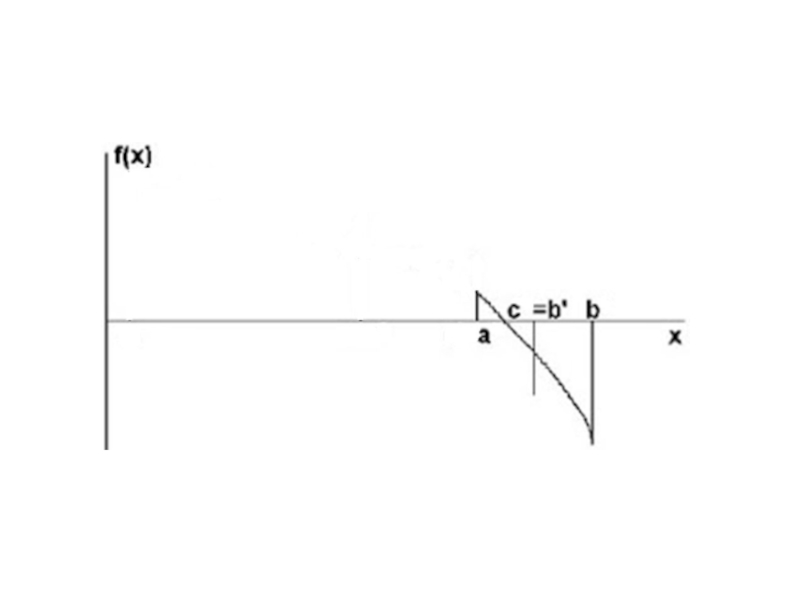
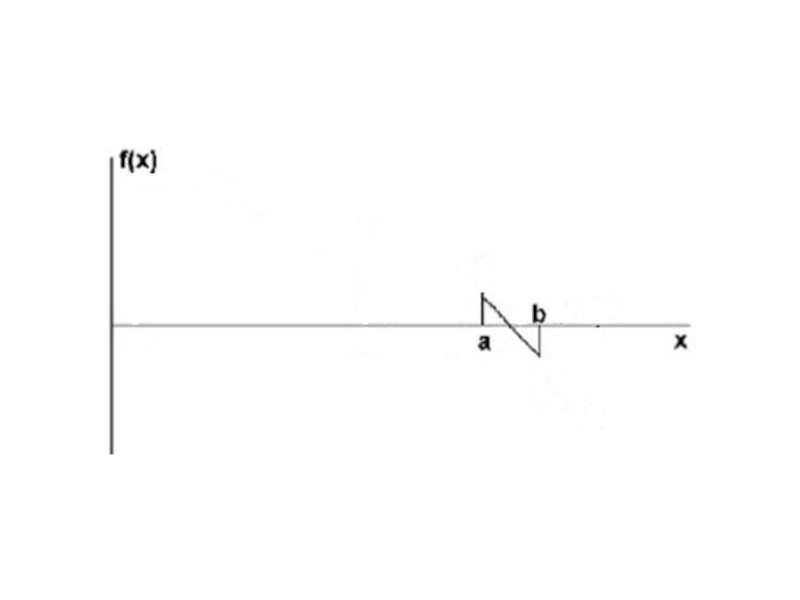
Слайд 7Аналитический метод отделения корней
1) Если непрерывная на отрезке
функция F(x)
принимает на его концах
значения разных знаков, то уравнение
F(x)=0
имеет на этом отрезке, по меньшей мере,
один корень
2) Если функция F(x) к тому же еще и
строго монотонна, то корень на отрезке
значения разных знаков, то уравнение
F(x)=0
имеет на этом отрезке, по меньшей мере,
один корень
2) Если функция F(x) к тому же еще и
строго монотонна, то корень на отрезке
единственный
Слайд 14Алгоритм данного метода:
1.Определить начальные данные (a, b, ε).
2.Если нужная точность достигнута
(| b - a | < ε) то п.6
3.Найти середину очередного отрезка (c=(a+b)/2).
4.Если значения функции в точках а и c одного знака (f(a)*f(c)>0), то в качестве следующего отрезка взять правую половину (а=c), иначе левую (b=c).
5.Иди к п.2.
6.Напечатать ответ (( a + b ) / 2 )
3.Найти середину очередного отрезка (c=(a+b)/2).
4.Если значения функции в точках а и c одного знака (f(a)*f(c)>0), то в качестве следующего отрезка взять правую половину (а=c), иначе левую (b=c).
5.Иди к п.2.
6.Напечатать ответ (( a + b ) / 2 )
Слайд 15Методом половинного деления уточнить корень уравнения
x4 + 2 x3 – x
– 1 = 0
лежащий на отрезке [0, 1].
лежащий на отрезке [0, 1].
Слайд 16Метод хорд
Применяется в том случае, когда f'(X) и f''(X) не изменяют
знака на отрезке [a,b], т.е. функция f(X) на отрезке [a,b] монотонна и не имеет точек перегиба
Слайд 19
Найти положительный корень уравнения (методом хорд)
x3 – 0,2 x2 –
0,2 х – 1,2 = 0
с точностью ε = 0,01.
с точностью ε = 0,01.
Слайд 20Метод Ньютона (касательной)
В качестве исходной точки х0 выбирается тот конец
интервала [а, b], которому отвечает ордината того же знака, что и знак f ″ (х).



![Отделение корней Корень уравнения f(х) = 0 считается отделенным на отрезке [a,b], если на этомотрезке](/img/tmb/1/80687/2b36f8f7a0df1dba0d23aaaf902d4737-800x.jpg)






![Метод Ньютона (касательной) В качестве исходной точки х0 выбирается тот конец интервала [а, b], которому](/img/tmb/1/80687/de4b165d9ee4132cb1a4bd8cf0f349c2-800x.jpg)