- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные виды уравнения прямой на плоскости презентация
Содержание
- 1. Различные виды уравнения прямой на плоскости
- 2. 1.Уравнение прямой с угловым коэффициентом: y=kx+b
- 3. Уравнение прямой, проходящей через точку М1(х1;у1) с
- 4. Уравнение прямой, проходящей через точку М1(х1;у1), но
- 5. Уравнение прямой, проходящей через две заданные точки
- 6. Уравнение прямой, проходящей через две заданные точки
- 7. Общее уравнение прямой на плоскости: Ax+By+C=0,
- 8. 1. Угловой коэффициент прямой, проходящей через две точки М1(х1;у1) и М2(х2;у2) ПРИЛОЖЕНИЯ
- 9. 2. Острый угол φ между прямыми,
- 10. 3. Точка пересечения прямых, заданных общими уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, находится как решение системы: ПРИЛОЖЕНИЯ
- 11. 4. Координаты x0 ,y0 середины отрезка M1 , M2 между точками М1(х1;у1) и М2(х2;у2) ПРИЛОЖЕНИЯ
- 12. 5. Расстояние |M1M2| между точками М1(х1;у1) и М2(х2;у2) ПРИЛОЖЕНИЯ
- 13. 6. Необходимое и достаточное условие параллельности двух
- 14. 7. Необходимое и достаточное условие перпендикулярности двух
- 15. Примеры: П р и м е р
- 16. Примеры: П р и м е р
- 17. Примеры: П р и м е р
- 18. Примеры: Найдем угловой коэффициент k1 прямой:
- 19. Нормальный вектор прямой Если вектор перпендикулярен
- 20. Нормальный вектор прямой Найти уравнение прямой
- 21. Расстояние от точки до прямой Теорема. Расстояние
- 22. Расстояние от точки до прямой Найти расстояние
- 23. Кривые второго порядка ОКРУЖНОСТЬ Определение 1.
- 24. Кривые второго порядка О К Р
- 25. Определение. Эллипс – геометрическое место точек на
- 26. Свойства: 1. Центр эллипса − точка О(0;0);
- 27. Кривые второго порядка Эллипс, задаваемый уравнением обладает свойствами: Э ллипс
- 28. Кривые второго порядка Определение. Гипербола
- 29. Свойства: Кривые второго порядка
- 30. Свойства: Кривые второго порядка
- 31. Гиперболы, задаваемые уравнениями:
- 32. Кривые второго порядка П А
- 33. Кривые второго порядка П А
- 34. Кривые второго порядка П А
- 35. Кривые второго порядка П А
1.Уравнение прямой с угловым коэффициентом: y=kx+b k- угловой коэффициент прямой α x y o b α - угол наклона прямой к оси Ох, где
Слайд 21.Уравнение прямой с угловым коэффициентом:
y=kx+b
k- угловой коэффициент прямой
α
x
y
o
b
α -
угол наклона прямой к оси Ох, где
b - ордината точки пересечения прямой с осью Оу
Слайд 3Уравнение прямой, проходящей через точку М1(х1;у1) с заданным угловым коэффициентом k,
при
α
x
y
o
М1(х1;у1)
x1
у1
Слайд 4Уравнение прямой, проходящей через точку М1(х1;у1), но не имеющей углового коэффициента,
при
Х=Х1
x
y
o
М1
x1
у1
Слайд 5Уравнение прямой, проходящей через две заданные точки М1(х1;у1) и М2(х2;у2)
x
y
o
y2
М1
x1
у1
М2
x2
y2
у1
М2
М1
y
x
o
x1
Слайд 7Общее уравнение прямой на плоскости:
Ax+By+C=0, где А,В,С – числа
Если
А=0 В=0 уравнение прямой принимает вид: у=у1 , прямая параллельна оси Ох, угловой коэффициент равен 0;
Если А=0 В=0 уравнение прямой принимает вид: х=х1, прямая параллельна оси Oy, углового коэффициента не имеет;
Если А=0 В=0, то уравнение прямой принимает вид:
y=kx+b, где: k=A / B
Если А=0 В=0 уравнение прямой принимает вид: х=х1, прямая параллельна оси Oy, углового коэффициента не имеет;
Если А=0 В=0, то уравнение прямой принимает вид:
y=kx+b, где: k=A / B
Слайд 92. Острый угол φ между прямыми,
заданными уравнениями
y=k1x+b1 и
y=k2x+b2 вычисляется по формуле:
ПРИЛОЖЕНИЯ
Слайд 103. Точка пересечения прямых,
заданных общими уравнениями
A1x+B1y+C1=0 и A2x+B2y+C2=0, находится как решение
системы:
ПРИЛОЖЕНИЯ
Слайд 136. Необходимое и достаточное
условие параллельности двух прямых
Необходимое и достаточное условие параллельности
двух прямых, имеющих угловые коэффициенты k1 и k2 :
k1=k2
k1=k2
ПРИЛОЖЕНИЯ
Слайд 147. Необходимое и достаточное условие перпендикулярности двух прямых
Необходимое и достаточное
условие перпендикулярности двух прямых, имеющих угловые коэффициенты k1 и k2 :
ПРИЛОЖЕНИЯ
Слайд 15Примеры:
П р и м е р 1. Дано общее уравнение прямой:
Найти
угловой коэффициент прямой.
Р е ш е н и е. Решим уравнение относительно у получим уравнение прямой с угловым коэффициентом:
Отсюда заключаем: k = 2/3 - угловой коэффициент прямой.
О т в е т: 2/3
Р е ш е н и е. Решим уравнение относительно у получим уравнение прямой с угловым коэффициентом:
Отсюда заключаем: k = 2/3 - угловой коэффициент прямой.
О т в е т: 2/3
Слайд 16Примеры:
П р и м е р 2. Составить уравнение прямой, проходящей
через точку А(-1;3) и составляющей с осью Ох угол 135о.
Р е ш е н и е. Так как в данном случае k=tg135o=-1 и x1=-1, y1=3, то уравнение прямой будет иметь вид: y-3=-1(x+1)
Отсюда получаем: у = -х+2 – искомое уравнение прямой.
О т в е т: у = -х+2
Р е ш е н и е. Так как в данном случае k=tg135o=-1 и x1=-1, y1=3, то уравнение прямой будет иметь вид: y-3=-1(x+1)
Отсюда получаем: у = -х+2 – искомое уравнение прямой.
О т в е т: у = -х+2
Слайд 17Примеры:
П р и м е р 3. Составить уравнение прямой, проходящей
через точку пересечения прямых:
параллельно прямой:
Р е ш е н и е. а) Найдем точку пересечения двух прямых, для этого, решим систему уравнений:
Следовательно, искомая точка пересечения – М1(7;-6)
б) Составим уравнение прямой, проходящей через данную точку М1(7;-6) параллельно прямой:
параллельно прямой:
Р е ш е н и е. а) Найдем точку пересечения двух прямых, для этого, решим систему уравнений:
Следовательно, искомая точка пересечения – М1(7;-6)
б) Составим уравнение прямой, проходящей через данную точку М1(7;-6) параллельно прямой:
Слайд 18Примеры:
Найдем угловой коэффициент k1 прямой:
Из условия параллельности двух прямых находим
угловой коэффициент искомой прямой: k1= k2=3
Пользуясь формулой: , находим уравнение прямой, проходящей через точку М1(7;-6) с угловым коэффициентом k2=3:
О т в е т:
Пользуясь формулой: , находим уравнение прямой, проходящей через точку М1(7;-6) с угловым коэффициентом k2=3:
О т в е т:
Слайд 19Нормальный вектор прямой
Если вектор перпендикулярен направляющему вектору прямой
, то он называется нормальным вектором прямой .
Прямая задана общим
уравнением
Тогда вектор
является нормальным вектором
этой прямой.
Слайд 20Нормальный вектор прямой
Найти уравнение
прямой , которая проходит
через
точку
и имеет нормальный вектор
.
и имеет нормальный вектор
.
Решение. Векторы
перпендикулярны, их скалярное произведение равно
нулю:
Это и есть искомое уравнение.
З
А
Д
А
Ч
А
Слайд 21Расстояние от точки до прямой
Теорема. Расстояние
от точки
до прямой, заданной
общим уравнением
вычисляется
формулой
Слайд 22Расстояние от точки до прямой
Найти расстояние от точки
до прямой,
заданной общим уравнением
заданной общим уравнением
Решение.
Ответ: 4.
З
А
Д
А
Ч
А
Слайд 23Кривые второго порядка
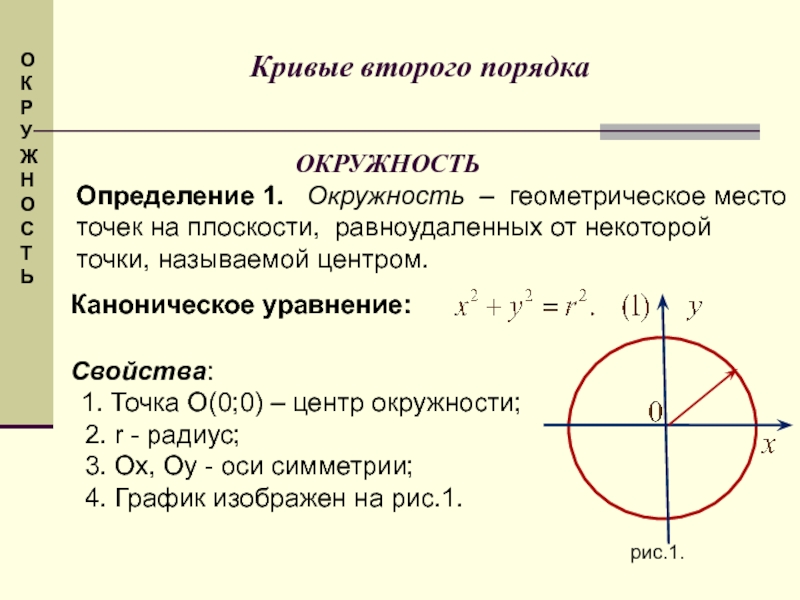
ОКРУЖНОСТЬ
Определение 1. Окружность – геометрическое место точек на
плоскости, равноудаленных от некоторой точки, называемой центром.
О
К
Р
У
Ж
Н
О
С
Т
Ь
Каноническое уравнение:
Свойства:
1. Точка О(0;0) – центр окружности;
2. r - радиус;
3. Ox, Oy - оси симметрии;
4. График изображен на рис.1.
рис.1.
Слайд 24Кривые второго порядка
О
К
Р
У
Ж
Н
О
С
Т
Ь
обладает свойствами:
Окружность, задаваемая уравнением
1.Точка
− центр окружности;
2. r − радиус;
3. Прямые −
оси симметрии;
4. График окружности (2) изображен
на рис.2 и получается из окружности с
уравнением (1) параллельным переносом
на вектор .
2. r − радиус;
3. Прямые −
оси симметрии;
4. График окружности (2) изображен
на рис.2 и получается из окружности с
уравнением (1) параллельным переносом
на вектор .
рис.2.
Слайд 25Определение. Эллипс – геометрическое место точек на плоскости, для каждой из
которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная.
Эллипс – геометрическое место точек на плоскости, координаты которых в некоторой прямоугольной системе координат Oxy удовлетворяет уравнению
При уравнение (1) является уравнением окружности радиуса с центром в начале координат.
Эллипс – геометрическое место точек на плоскости, координаты которых в некоторой прямоугольной системе координат Oxy удовлетворяет уравнению
При уравнение (1) является уравнением окружности радиуса с центром в начале координат.
Э
ллипс
Кривые второго порядка
Слайд 26Свойства:
1. Центр эллипса − точка О(0;0);
2. Вершины эллипса − точки
3.
− оси эллипса;
4. -− полуоси эллипса;
5. Оси симметрии − Оx, Oy;
6. Фокусы эллипса – точки, где если
где если
4. -− полуоси эллипса;
5. Оси симметрии − Оx, Oy;
6. Фокусы эллипса – точки, где если
где если
Э
ллипс
Кривые второго порядка
Слайд 28Кривые второго порядка
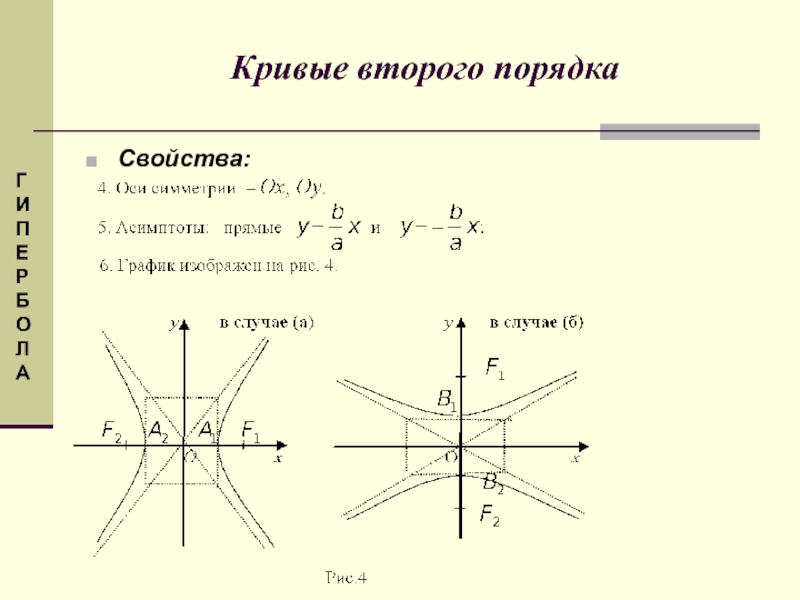
Определение. Гипербола – геометрическое место точек на плоскости,
для каждой из которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная.
Каноническое уравнение:
(а) или (б)
Каноническое уравнение:
(а) или (б)
ГИПЕРБОЛА
Слайд 32Кривые второго порядка
П
А
Р
А
Б
О
Л
А
где некоторое
число, называемое параметром параболы.
Ось абсцисс Ox является осью симметрии параболы.
Ось абсцисс Ox является осью симметрии параболы.
Определение. Парабола – геометрическое место точек на плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Каноническое уравнение:
Каноническое уравнение:
Каноническое уравнение:
или
Слайд 33Кривые второго порядка
П
А
Р
А
Б
О
Л
А
Свойства:
Вершина: О(0;0);
Фокусы параболы:
или
Директриса: или
Параболы, задаваемые уравнениями
или ,
где некоторое число, называемое параметром параболы,
обладают свойствами:
Директриса: или
Параболы, задаваемые уравнениями
или ,
где некоторое число, называемое параметром параболы,
обладают свойствами:
Слайд 34Кривые второго порядка
П
А
Р
А
Б
О
Л
А
;
Вершина: точка
Фокусы параболы:
или
Директриса: или
Оси симметрии: или .
Директриса: или
Оси симметрии: или .
Слайд 35Кривые второго порядка
П
А
Р
А
Б
О
Л
А
;
Уравнение второй степени
где числа А и С
не равны одновременно нулю, преобразуется к каноническому виду методом выделения полных квадратов и последующим параллельным переносом.
Тип кривой определяется числами А и С:
Если , то – окружность;
если и то – эллипс;
если , то – гипербола;
если одно из чисел А или С равно нулю, то – парабола.
