- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Равнобедренный треугольник и его свойства презентация
Содержание
- 1. Равнобедренный треугольник и его свойства
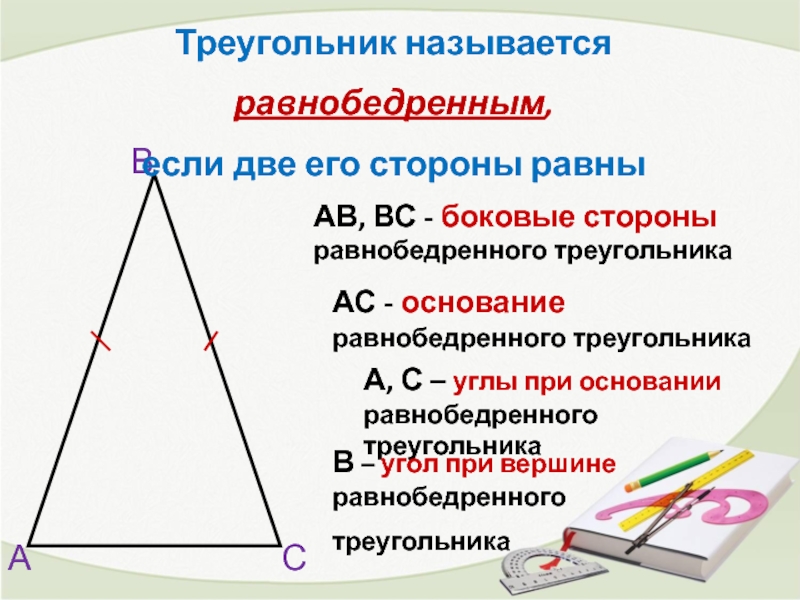
- 2. А В С АВ, ВС -
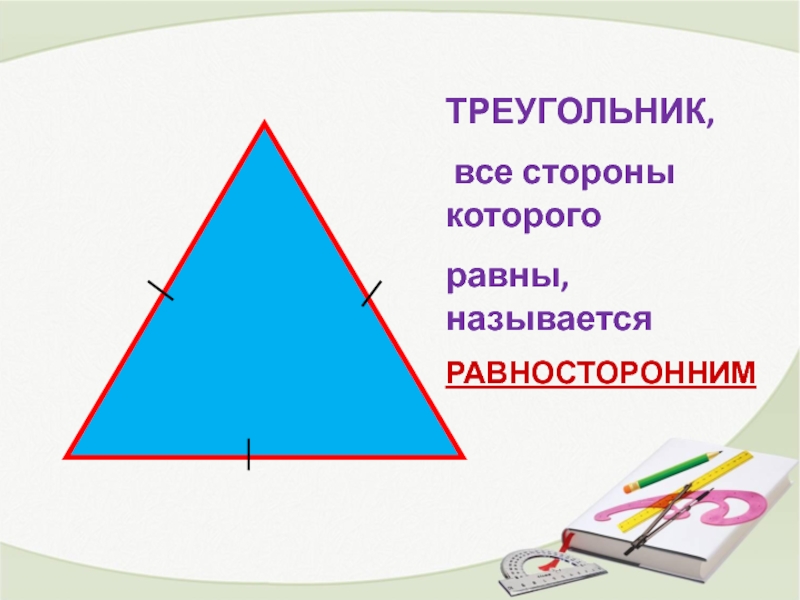
- 3. ТРЕУГОЛЬНИК, все стороны которого равны, называется РАВНОСТОРОННИМ
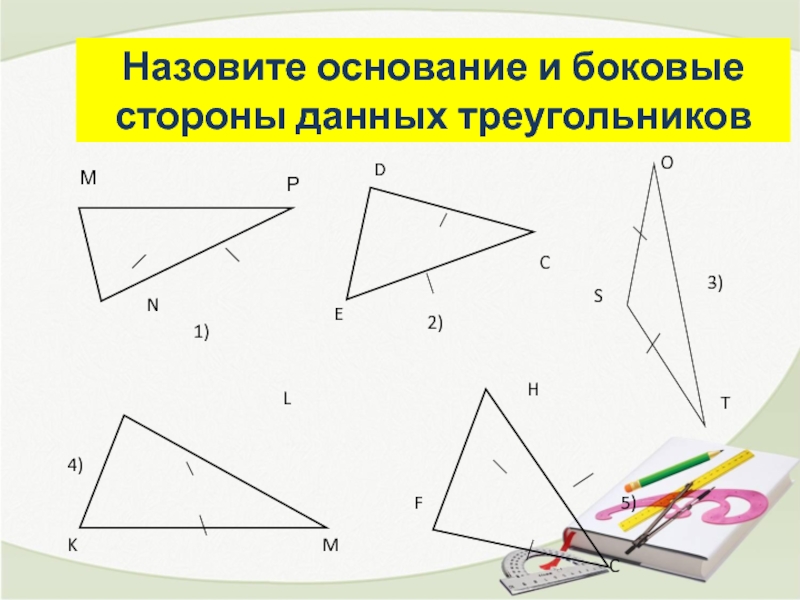
- 4. Назовите основание и боковые стороны данных треугольников
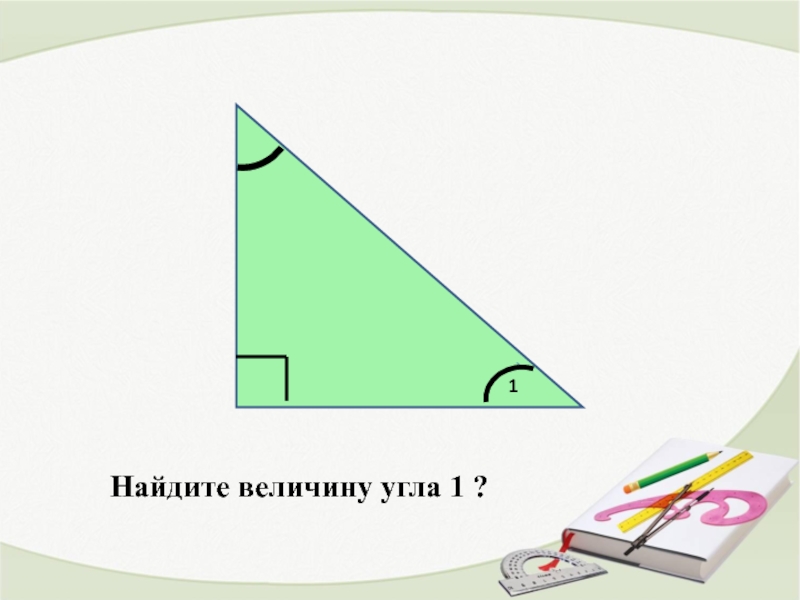
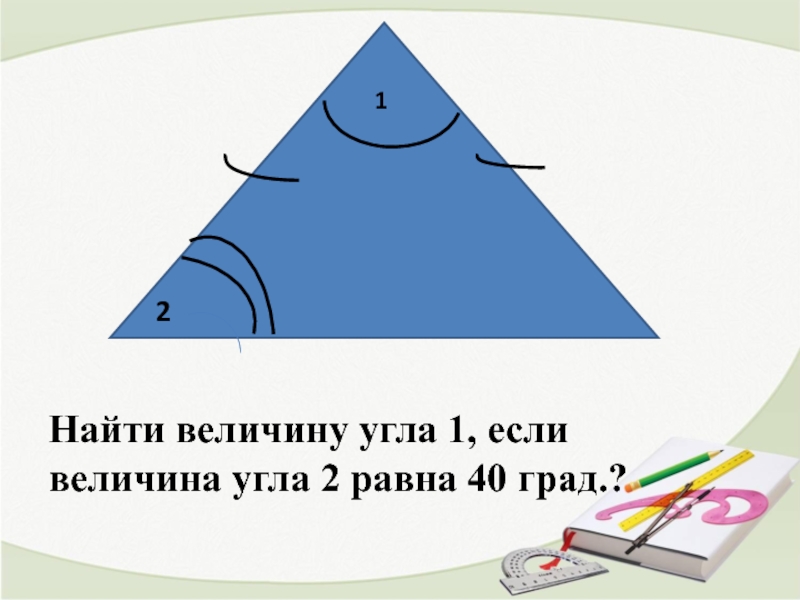
- 5. Найдите величину угла 1 ? 1
- 6. 1 Найти величину
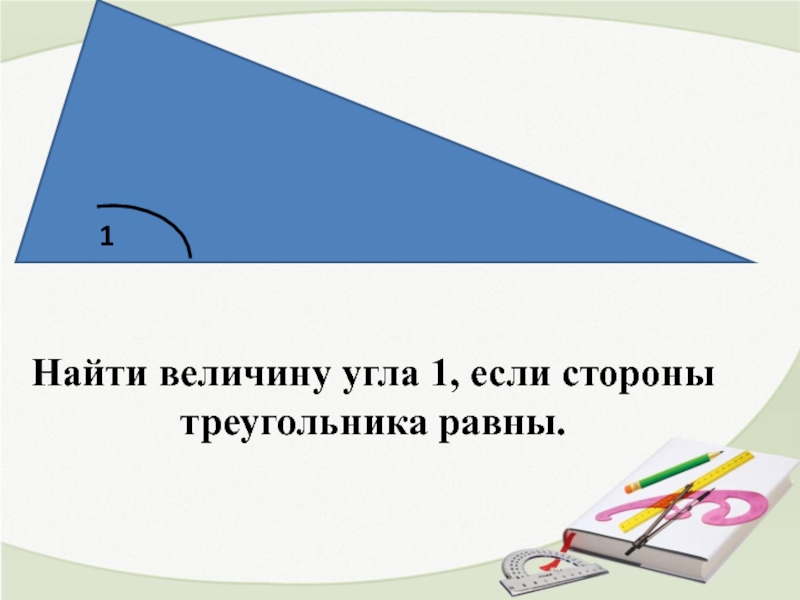
- 7. Найти величину угла 1, если стороны треугольника равны. 1
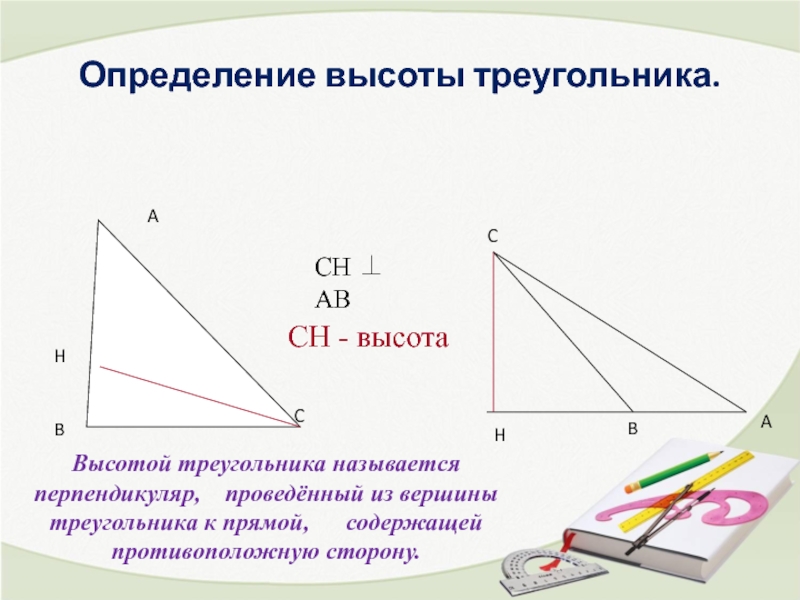
- 8. Определение высоты треугольника. Высотой треугольника называется перпендикуляр,
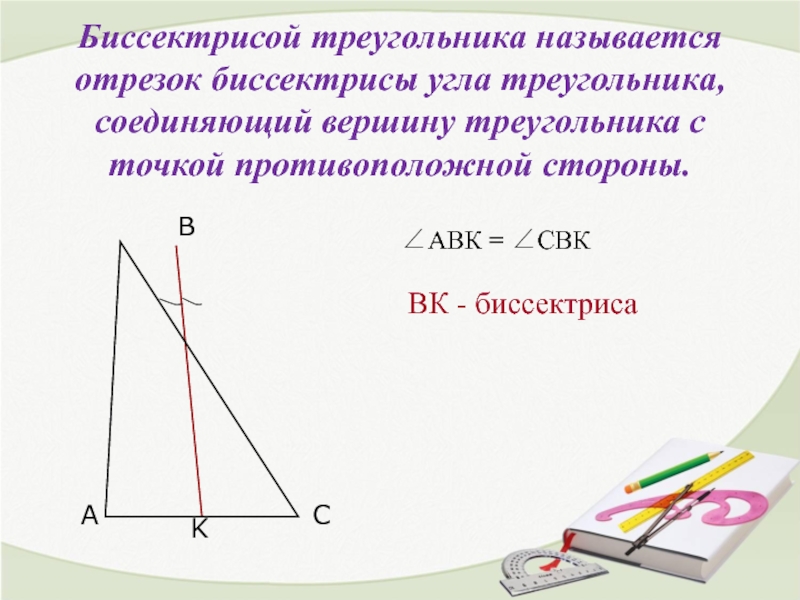
- 9. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника,
- 10. Медианой треугольника называется отрезок, соединяющий вершину треугольника
- 11. \ \ \
- 12. , 3 а
- 13. Меч диван а медиана
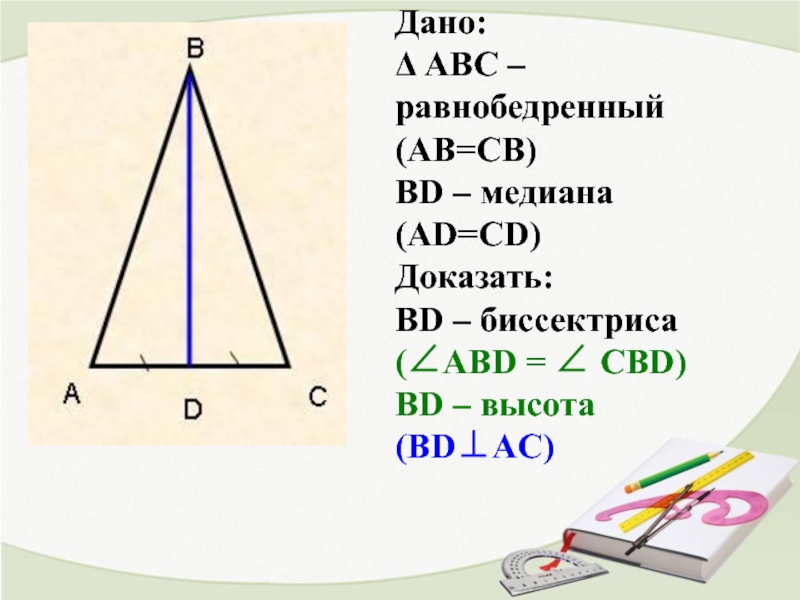
- 14. Дано: Δ АВС – равнобедренный
- 16. Доказательство: Δ AВD = Δ
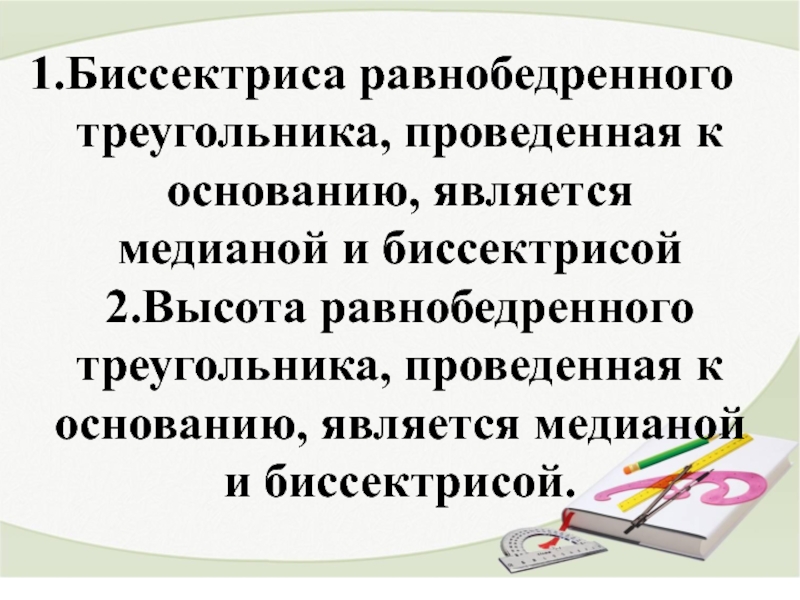
- 17. Биссектриса равнобедренного треугольника, проведенная
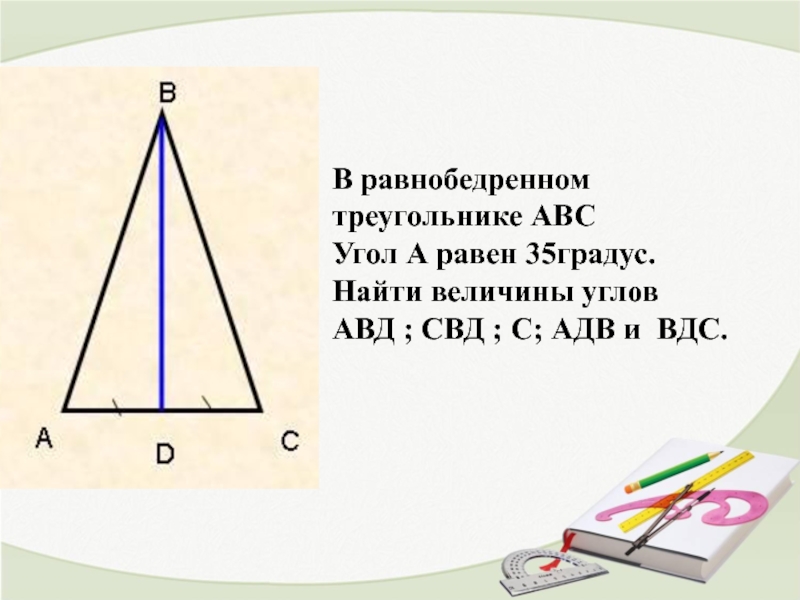
- 18. В равнобедренном треугольнике АВС Угол
- 19. ТЕСТ.
- 20. Домашнее задание: п.25-26, контрольные вопросы
- 21. Красивые здания, картины создаются с учетом принципа
- 22. Где в жизни встречаются равнобедренные треугольники?
- 23. Оцените “уровень успешности”: Пришлите «5»— если вам
- 25. Таблицы. Справочные материалы. (Дополнительный файл)
А В С АВ, ВС - боковые стороны равнобедренного треугольника А, С – углы при основании равнобедренного треугольника АС - основание равнобедренного треугольника В – угол при вершине равнобедренного
![](/img/tmb/4/398113/60994b518e11e9ae98a7e56a6dc32213-800x.jpg "Свойство медианы равнобедренного треугольника./\")
Слайд 2
А
В
С
АВ, ВС - боковые стороны равнобедренного треугольника
А, С – углы при
основании равнобедренного треугольника
АС - основание равнобедренного треугольника
В – угол при вершине равнобедренного
треугольника
Треугольник называется
равнобедренным,
если две его стороны равны
Слайд 8Определение высоты треугольника.
Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника
к прямой, содержащей противоположную сторону.
СН - высота
СН ⊥ АВ
Слайд 9Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны.
ВК - биссектриса
∠АВК = ∠СВК
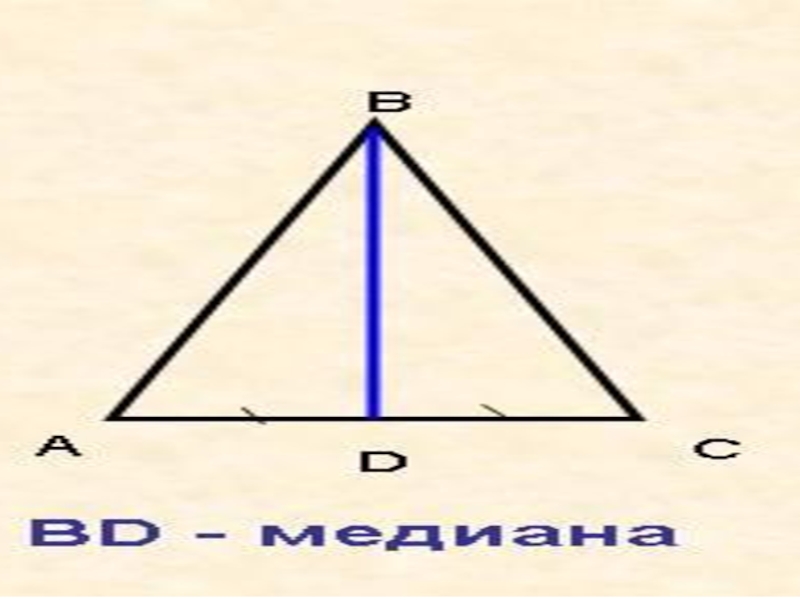
Слайд 10Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны
АМ
– медиана
ВМ = МС
Слайд 14
Дано:
Δ АВС – равнобедренный (АВ=СВ)
ВD – медиана (AD=СD)
Доказать:
ВD – биссектриса (∠AВD
= ∠ CBD)
ВD – высота (ВD⊥AС)
ВD – высота (ВD⊥AС)
Слайд 16
Доказательство:
Δ AВD = Δ CBD (по первому признаку равенства треугольников), т.к.
AД=CД
(по условию)
AВ=СB (треугольник АВС - равнобедренный)
∠A = ∠B (по свойству углов при основании равнобедренного треугольника)
Δ AВD = Δ CBD ⇒
∠ACD = ∠ BCD ⇒ CD – биссектриса
∠ ADC = ∠ BDC ⇒ ∠ ADC и ∠ BDC - смежные ⇒ ∠ ADC = ∠ BDC = 90°
⇒ CD⊥AB ⇒ CD – высота.
Что и требовалось доказать.
AВ=СB (треугольник АВС - равнобедренный)
∠A = ∠B (по свойству углов при основании равнобедренного треугольника)
Δ AВD = Δ CBD ⇒
∠ACD = ∠ BCD ⇒ CD – биссектриса
∠ ADC = ∠ BDC ⇒ ∠ ADC и ∠ BDC - смежные ⇒ ∠ ADC = ∠ BDC = 90°
⇒ CD⊥AB ⇒ CD – высота.
Что и требовалось доказать.
Слайд 17
Биссектриса равнобедренного треугольника, проведенная к основанию, является
медианой и биссектрисой
2.Высота равнобедренного
треугольника, проведенная к основанию, является медианой и биссектрисой.
Слайд 18
В равнобедренном треугольнике АВС
Угол А равен 35градус.
Найти величины углов
АВД ; СВД
; С; АДВ и ВДС.
Слайд 20 Домашнее задание: п.25-26, контрольные вопросы 8-11. Дома просмотреть презентацию. Записать
в тетрадь формулировку и доказательство теоремы и сделать рисунок.
• Творческое задание: из 6 спичек сделать 4 равносторонних треугольника.
Слайд 21Красивые здания, картины создаются с учетом принципа “золотого треугольника”. Все это
построено на связанных между собой математических пропорциях, в сечении получается звезда, где пять равнобедренных треугольников, они называются “золотыми”.
Слайд 22Где в жизни встречаются равнобедренные треугольники?
Для желающих: подготовить презентацию:• Крыши домов,
башен; Орнаменты; Арки мостов; Египетские пирамиды; Северные росписи…
Слайд 23Оцените “уровень успешности”:
Пришлите «5»— если вам все было понятно и вы
справились с заданиями,
«4»– если кое-что непонятно
и
«3»– если все непонятно и срочно нужна помощь.
«4»– если кое-что непонятно
и
«3»– если все непонятно и срочно нужна помощь.
