Геометрические задачи «С2»
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расстояние между скрещивающимися прямыми презентация
Содержание
- 1. Расстояние между скрещивающимися прямыми
- 2. Тренировочная работа №3 Расстояние между скрещивающимися прямыми С2
- 3. Повторение: Если две прямые скрещиваются, то
- 4. Повторение: Отрезок, имеющий концы на двух
- 5. D А В С D1
- 6. D А В С
- 7. В правильной четырехугольной пирамиде SАВСД, все
- 8. Критерии оценивания выполнения задания С2
- 9. В правильной шестиугольной призме А…..F1,
- 10. В единичном кубе АВСДА1В1С1Д1 найдите расстояние
- 11. В правильной треугольной призме АВСА1В1С1
- 12. В единичном кубе АВСДА1В1С1Д1 найдите расстояние
- 13. 1. В.А. Смирнов ЕГЭ 2011. Математика. Задача
Слайд 1МОУ СОШ № 25 г. Крымска Малая Е.В.
Презентация по
Слайд 3
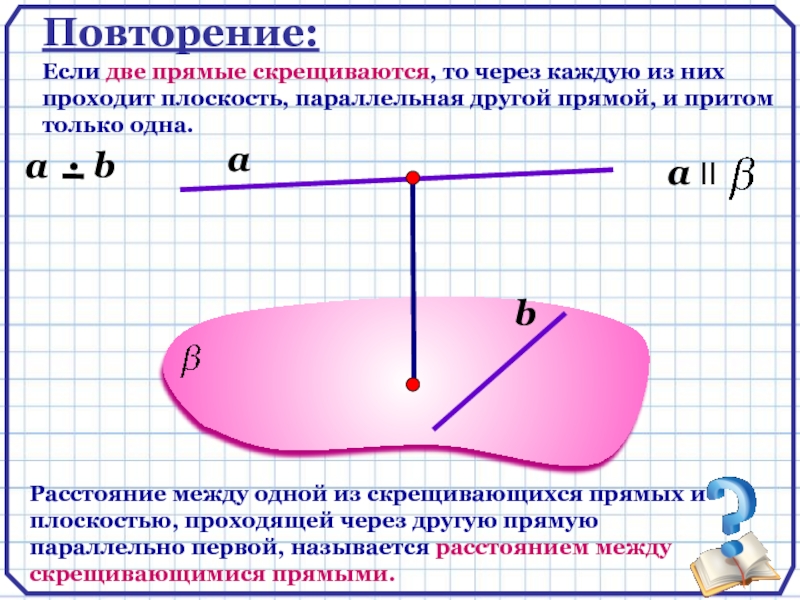
Повторение:
Если две прямые скрещиваются, то через каждую из них проходит плоскость,
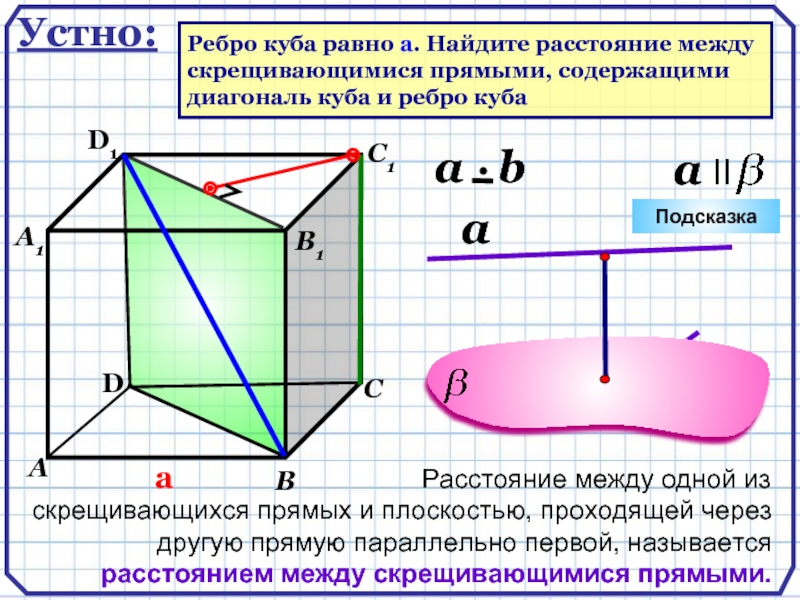
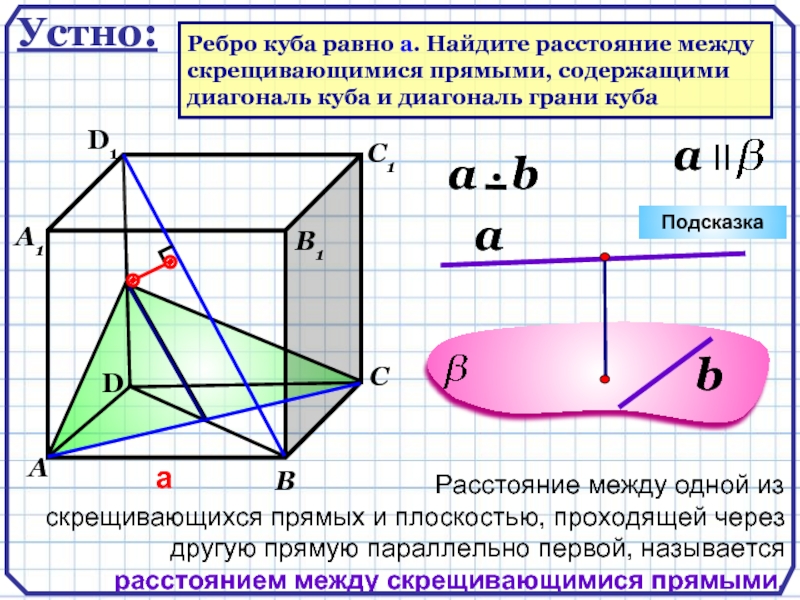
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
a
b
Слайд 4
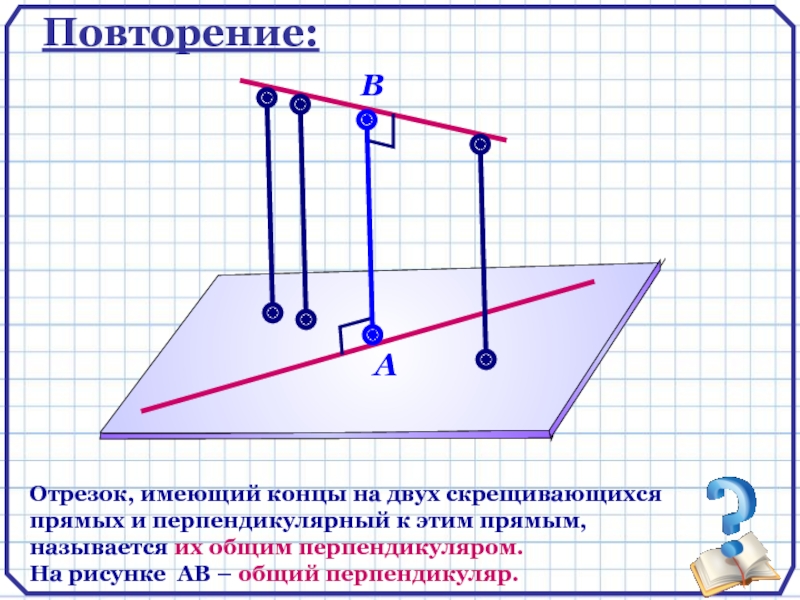
Повторение:
Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим
На рисунке АВ – общий перпендикуляр.
Слайд 5
D
А
В
С
D1
С1
а
В1
А1
Подсказка
Устно:
Ребро куба равно а. Найдите расстояние между
скрещивающимися прямыми, содержащими
диагональ
Слайд 6
D
А
В
С
D1
С1
а
В1
А1
Подсказка
Устно:
Ребро куба равно а. Найдите расстояние между
скрещивающимися прямыми, содержащими
диагональ
Слайд 7
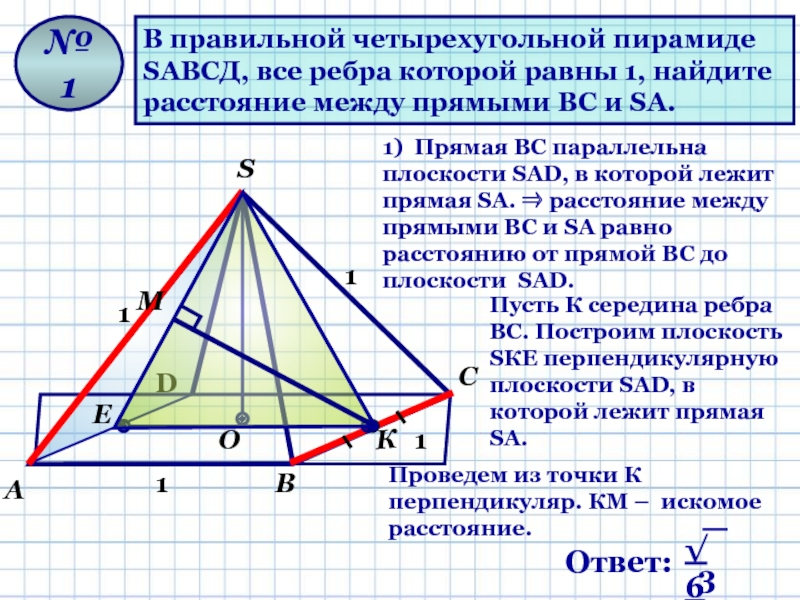
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1, найдите
расстояние
Е
№ 1
1) Прямая ВС параллельна плоскости SAD, в которой лежит прямая SA. ⇒ расстояние между прямыми ВС и SА равно расстоянию от прямой ВС до плоскости SAD.
Пусть К середина ребра ВС. Построим плоскость SКЕ перпендикулярную
плоскости SAD, в которой лежит прямая SA.
Проведем из точки К перпендикуляр. КМ – искомое расстояние.
М
1
1
1
1
Слайд 9
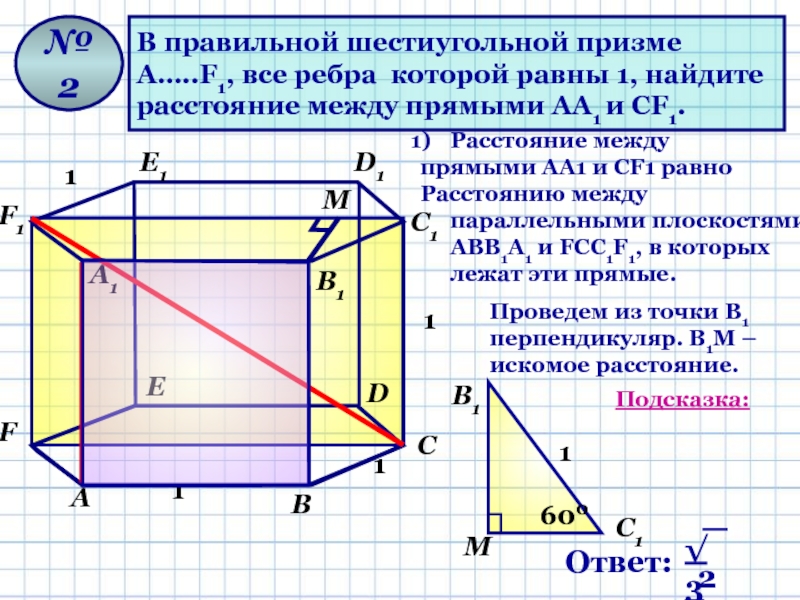
В правильной шестиугольной призме
А…..F1, все ребра которой равны 1, найдите
расстояние между прямыми АА1 и СF1.
№ 2
1
1
1
1
М
Расстояние между
прямыми АА1 и СF1 равно
Расстоянию между параллельными плоскостями АВВ1А1 и FCC1F1, в которых лежат эти прямые.
Проведем из точки В1 перпендикуляр. В1М –
искомое расстояние.
Подсказка:
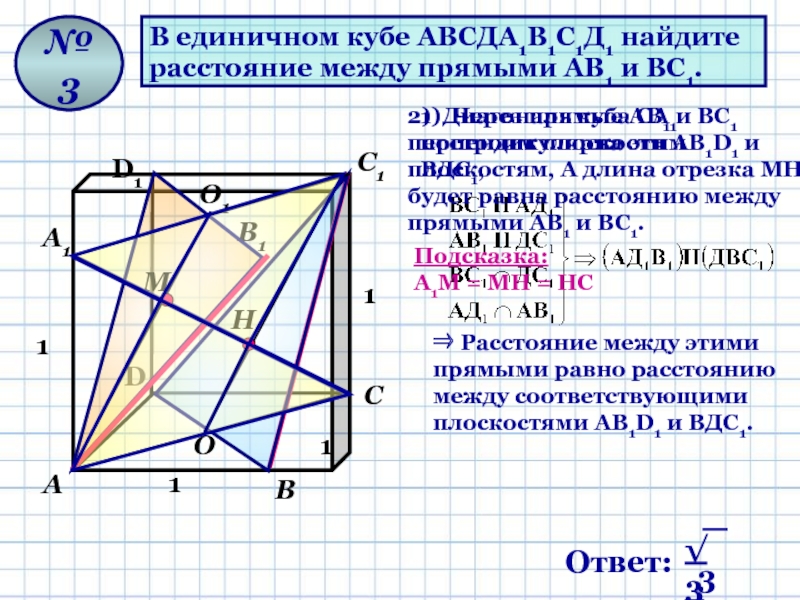
Слайд 10В единичном кубе АВСДА1В1С1Д1 найдите
расстояние между прямыми АВ1 и ВС1.
№
1
1
1
1
М
1) Через прямые АВ1 и ВС1 построим плоскости AВ1D1 и ВДС1,
⇒ Расстояние между этими прямыми равно расстоянию между соответствующими плоскостями AВ1D1 и ВДС1.
О
О1
Н
2) Диагональ куба СА1 перпендикулярна этим плоскостям, А длина отрезка МН будет равна расстоянию между прямыми АВ1 и ВС1.
Подсказка:
А1М = МН = НС
Слайд 11
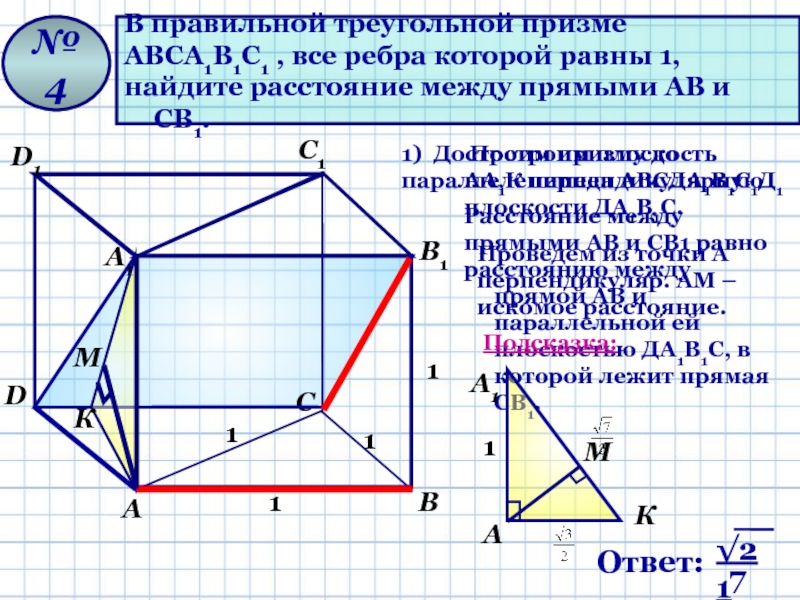
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите
№ 4
1
1
1
1
1) Достроим призму до параллелепипеда АВСДА1В1С1Д1
М
D
D1
Расстояние между
прямыми АВ и СВ1 равно
расстоянию между прямой АВ и параллельной ей плоскостью ДА1В1С, в которой лежит прямая СВ1.
Построим плоскость АА1К перпендикулярную
плоскости ДА1В1С.
К
Проведем из точки А перпендикуляр. АМ –
искомое расстояние.
Подсказка:
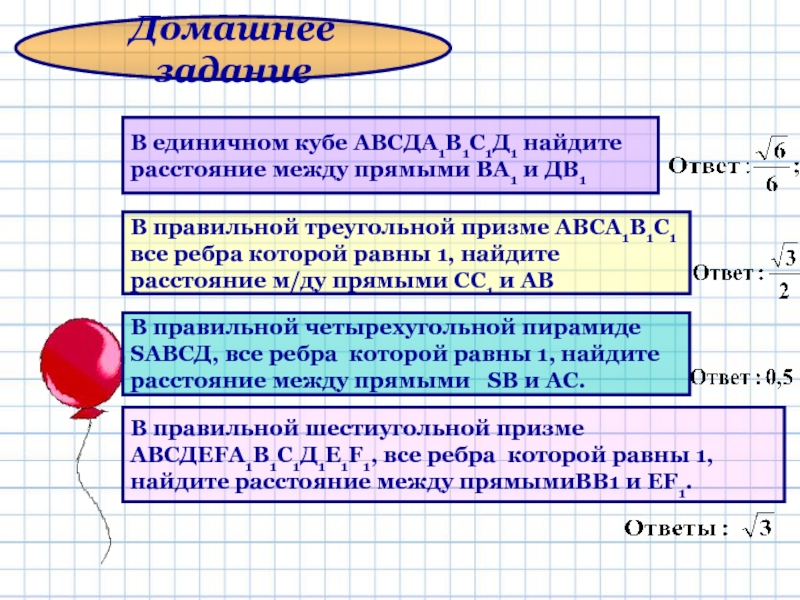
Слайд 12В единичном кубе АВСДА1В1С1Д1 найдите
расстояние между прямыми ВА1 и ДВ1
Домашнее
В правильной шестиугольной призме
АВСДЕFА1В1С1Д1Е1F1, все ребра которой равны 1,
найдите расстояние между прямымиВВ1 и ЕF1.
В правильной треугольной призме АВСА1В1С1
все ребра которой равны 1, найдите
расстояние м/ду прямыми СС1 и АВ
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1, найдите
расстояние между прямыми SВ и АС.
Слайд 131. В.А. Смирнов ЕГЭ 2011. Математика. Задача С2. Геометрия. Стереометрия. /
2. http://le-savchen.ucoz.ru/
Литература