- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Работа с одной выборкой. Парные сравнения презентация
Содержание
- 1. Работа с одной выборкой. Парные сравнения
- 2. Анализ единственной выборки Определение шкалы измерения. Проверка
- 3. Актуальные области интересов:
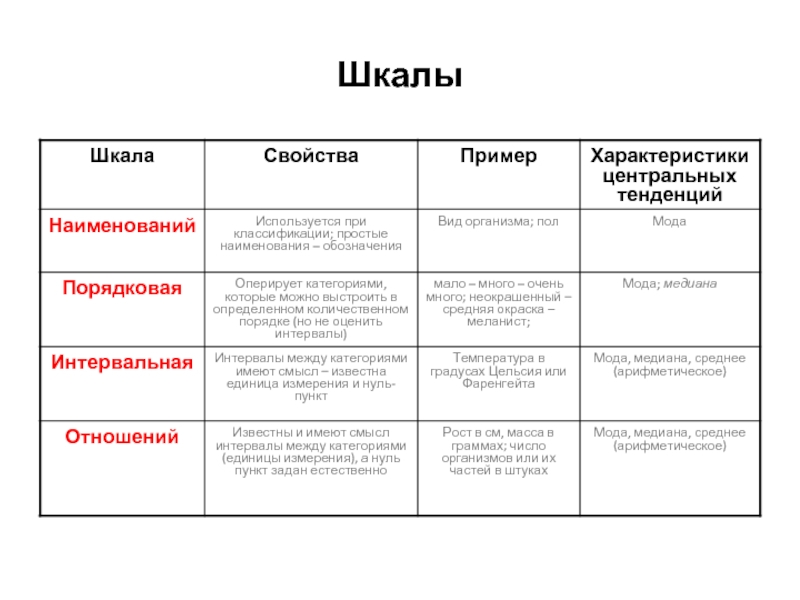
- 4. Шкалы
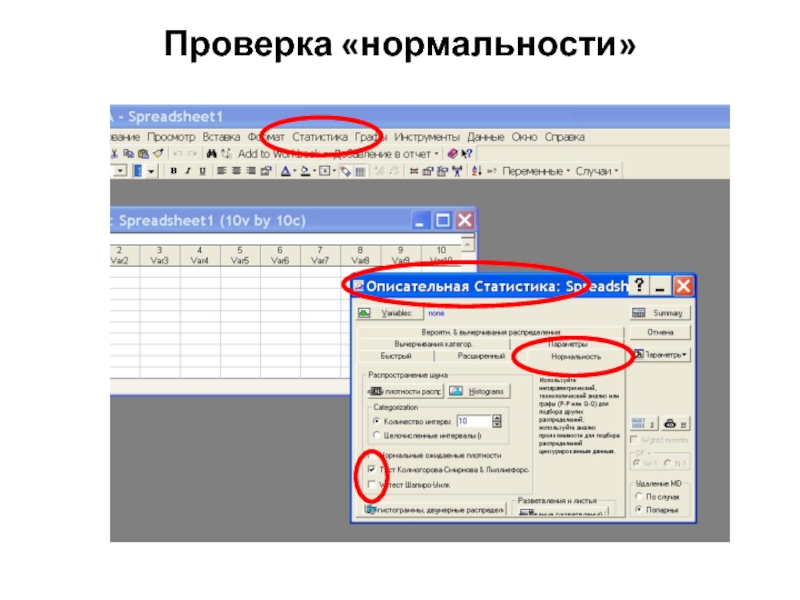
- 5. Проверка «нормальности»
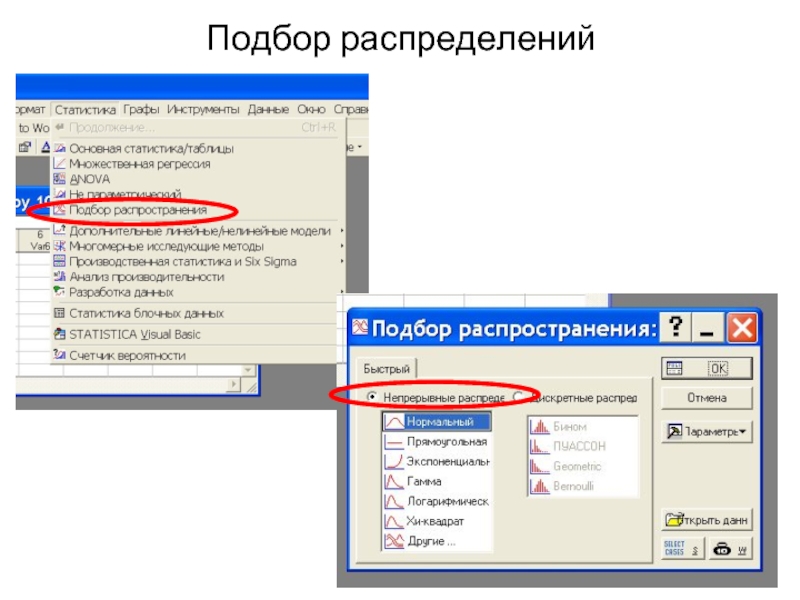
- 6. Подбор распределений
- 7. Трансформации переменных Попробуем логарифмировать значения переменных «Cu_кисл»,
- 8. Трансформации переменных
- 9. Что можно сравнивать? Центральную тенденцию – среднее,
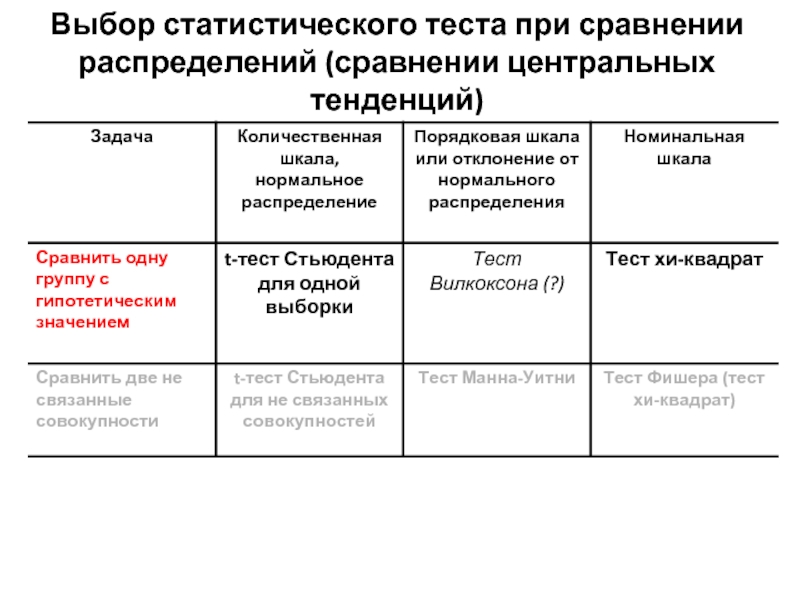
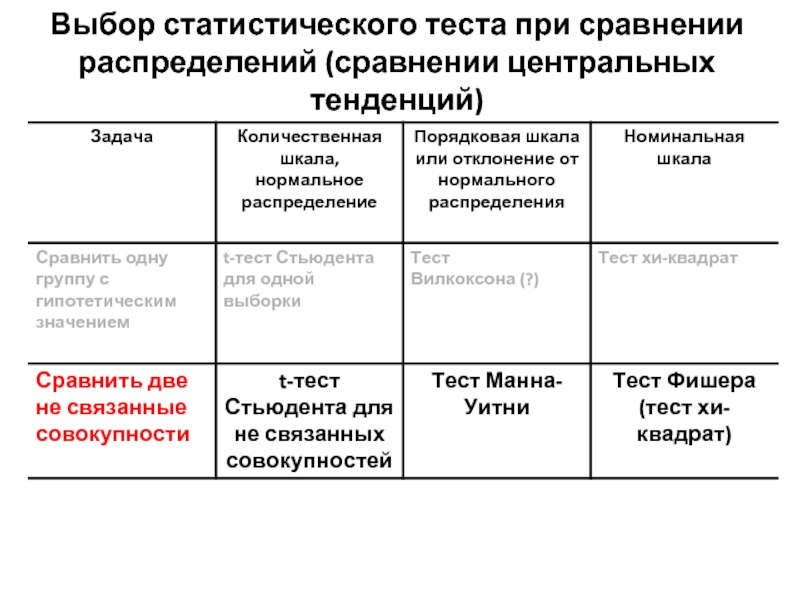
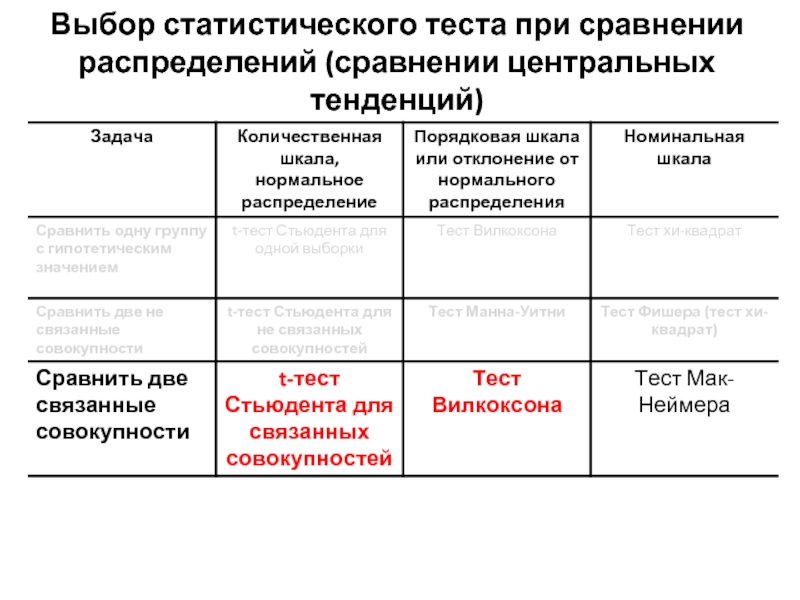
- 10. Выбор статистического теста при сравнении распределений (сравнении центральных тенденций)
- 11. Сравнить группу с гипотетическим значением. Количественная шкала,
- 12. Сравнить группу с гипотетическим значением. Номинальная шкала.
- 13. Сравнить группу с гипотетическим значением. Номинальная шкала.
- 14. Сравнить группу с гипотетическим значением. Номинальная шкала. Работаем с листом «Распределения» файла «Пример_тм_токсичность_проверка.xls»
- 15. Выбор статистического теста при сравнении распределений (сравнении центральных тенденций)
- 16. Сравнить две не связанные совокупности. Количественная шкала,
- 17. М1=8,68; М2=4,68; df=47; t=47,04; P
- 18. t-тест Стьюдента для не связанных совокупностей Два
- 19. Сравнить две не связанные совокупности. Порядковая
- 20. Тест Манна-Уитни Me1=1,5; Me3=15,0; U(n1=24; n3=25)=0,00; P
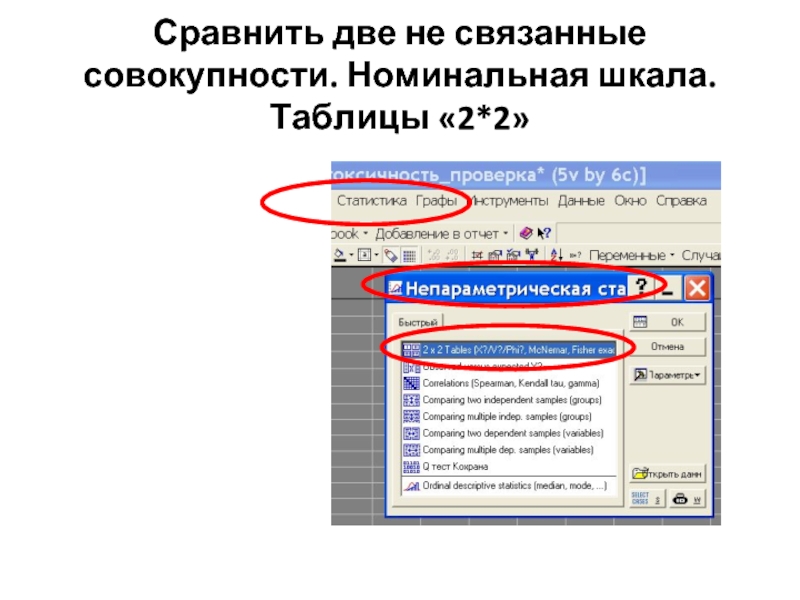
- 21. Сравнить две не связанные совокупности. Номинальная шкала. Таблицы «2*2»
- 22. Сравнить две не связанные совокупности. Номинальная шкала:
- 23. Сравнить две не связанные совокупности. Номинальная шкала: Хи-квадрат и др.
- 24. Сравнить две не связанные совокупности. Номинальная шкала:
- 25. Выбор статистического теста при сравнении распределений (сравнении центральных тенденций)
- 26. Сравнение трех выборок (критерий Краскела-Уолиса) H (2,
- 27. Сравнение четырех выборок (линии 1- 4) (критерий
Слайд 2Анализ единственной выборки
Определение шкалы измерения.
Проверка «нормальности» распределения для количественных данных /
Попытки преобразования «ненормально» распределенных переменных / анализ и поиск источников гетерогенности в многомодальных распределениях.
Проверка предположения об отличии значения в выборки от какой-либо константы.
Подгонка, т.е. определение типа распределения.
Слайд 7Трансформации переменных
Попробуем логарифмировать значения переменных «Cu_кисл», «Cd_кисл», «Pb_кисл», «Zn_кисл» в файле
Формула натурального логарифма в «STATISTICA»: =log(x)
Слайд 9Что можно сравнивать?
Центральную тенденцию – среднее, медиану.
Дисперсию, т.е. характер изменчивости.
Тип распределения
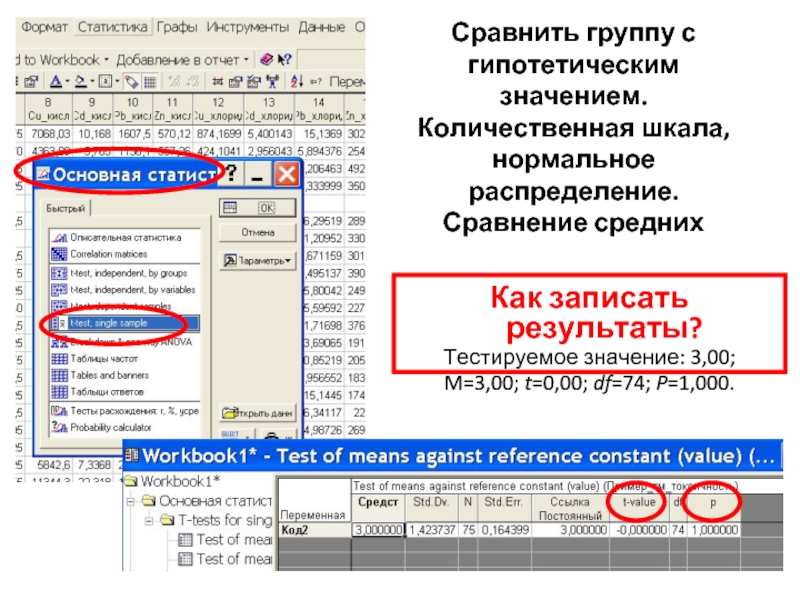
Слайд 11Сравнить группу с гипотетическим значением. Количественная шкала, нормальное распределение. Сравнение средних
Как
Тестируемое значение: 3,00;
M=3,00; t=0,00; df=74; P=1,000.
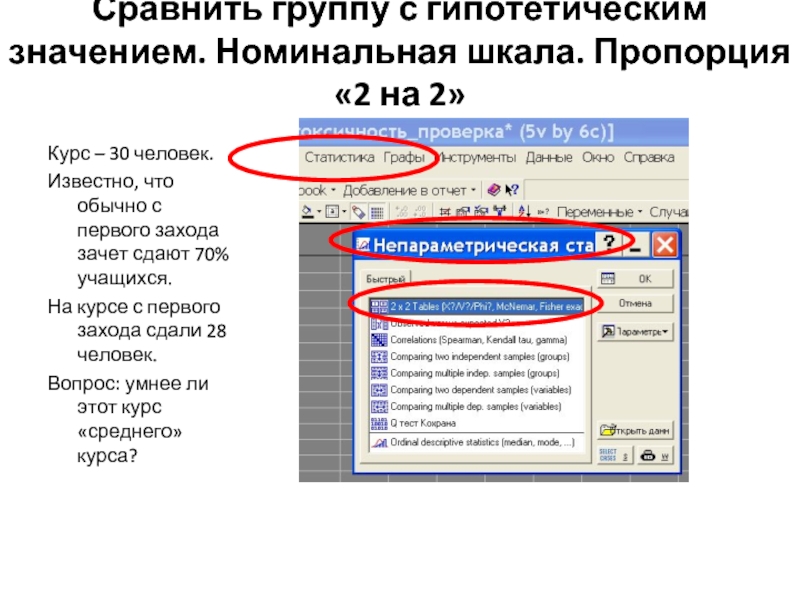
Слайд 12Сравнить группу с гипотетическим значением. Номинальная шкала. Пропорция «2 на 2»
Курс
Известно, что обычно с первого захода зачет сдают 70% учащихся.
На курсе с первого захода сдали 28 человек.
Вопрос: умнее ли этот курс «среднего» курса?
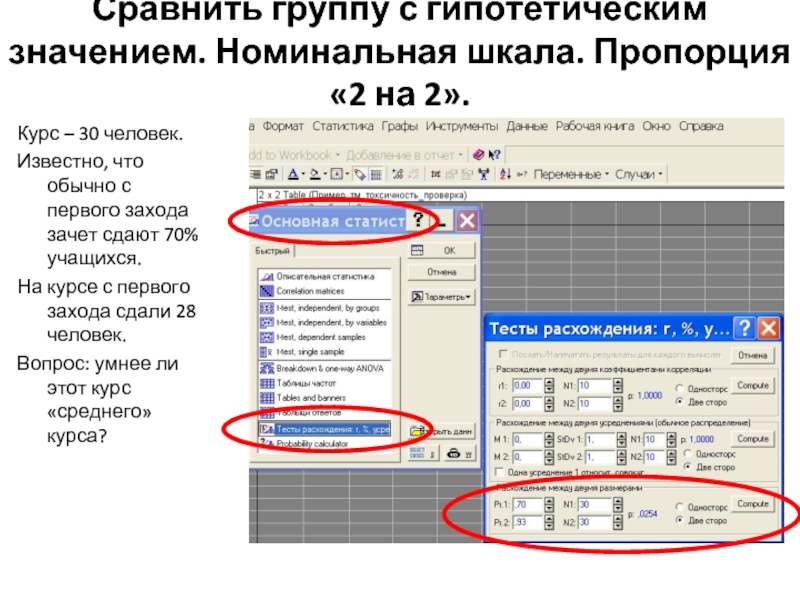
Слайд 13Сравнить группу с гипотетическим значением. Номинальная шкала. Пропорция «2 на 2».
Курс
Известно, что обычно с первого захода зачет сдают 70% учащихся.
На курсе с первого захода сдали 28 человек.
Вопрос: умнее ли этот курс «среднего» курса?
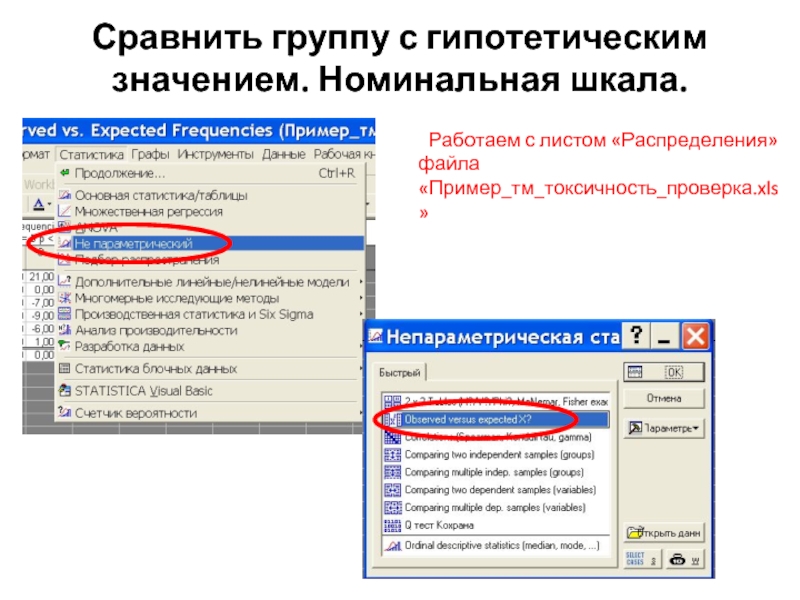
Слайд 14Сравнить группу с гипотетическим значением. Номинальная шкала.
Работаем с листом «Распределения» файла
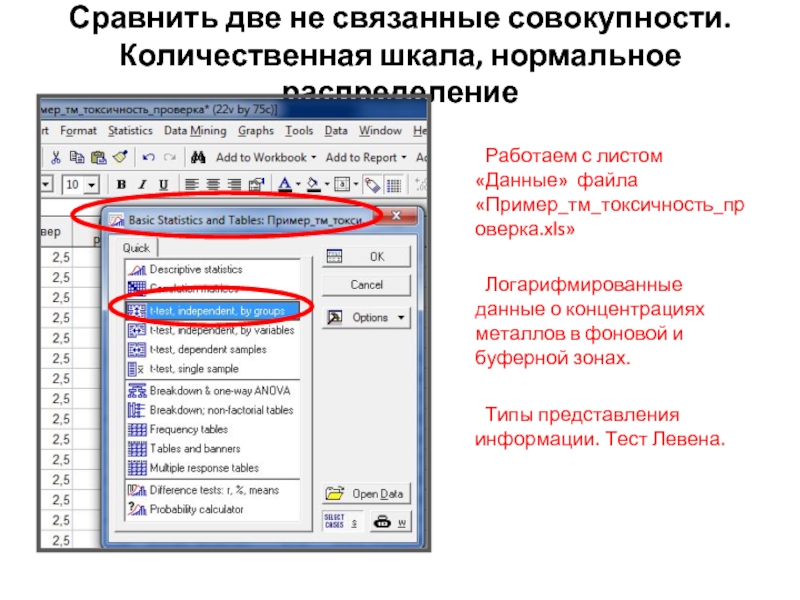
Слайд 16Сравнить две не связанные совокупности. Количественная шкала, нормальное распределение
Работаем с листом
Логарифмированные данные о концентрациях металлов в фоновой и буферной зонах.
Типы представления информации. Тест Левена.
Слайд 18t-тест Стьюдента для не связанных совокупностей
Два типа организации файла.
Число измерений в
Условия использования:
Всего ДВЕ выборки;
Нормальное распределение в каждой;
Равенство дисперсий в двух выборках;
n>10;
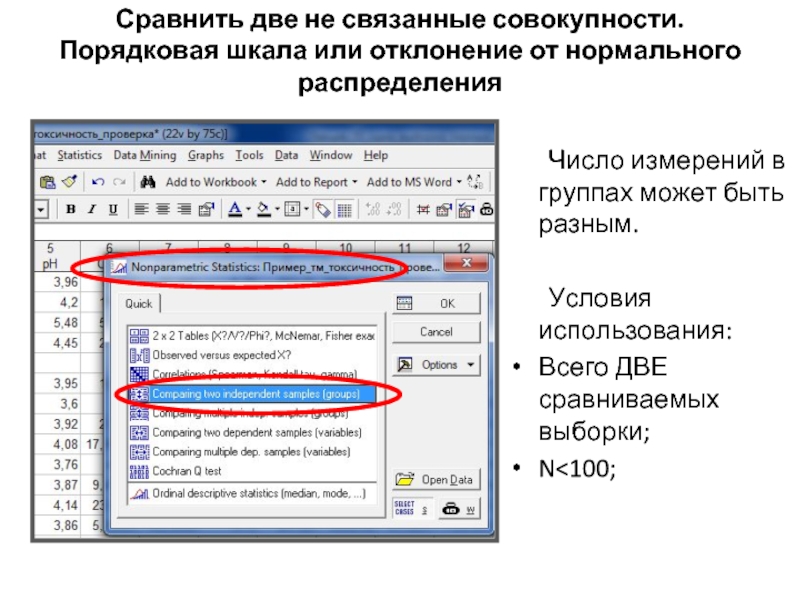
Слайд 19Сравнить две не связанные совокупности. Порядковая шкала или отклонение от нормального
Число измерений в группах может быть разным.
Условия использования:
Всего ДВЕ сравниваемых выборки;
N<100;
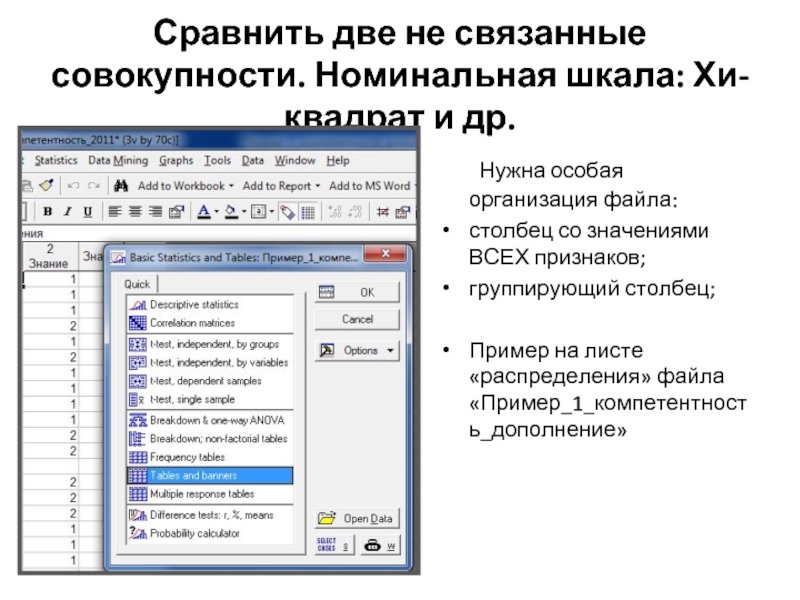
Слайд 22Сравнить две не связанные совокупности. Номинальная шкала: Хи-квадрат и др.
Нужна особая
столбец со значениями ВСЕХ признаков;
группирующий столбец;
Пример на листе «распределения» файла «Пример_1_компетентность_дополнение»
Слайд 24Сравнить две не связанные совокупности. Номинальная шкала: Хи-квадрат и др.
«Ручной» расчет
Слайд 26Сравнение трех выборок (критерий Краскела-Уолиса) H (2, N=55)=8.5, p=0.01
Попарное сравнение выборок
Линия 1 – линия 2: p=0.04 Линия 1 – линия 3: p=0.01 Линия 2 – линия 3: p=0.74
N=26 N=13 N=16
Удельная активность 90Sr в костной ткани
Apodemus uralensis
Удельная активность 90Sr в костной ткани малой лесной мыши составляет 29±2 Бк/г (указано среднее значение и стандартная ошибка средней, N=55)
Модоров М.В., Селезнев А.А. Пространственно-временная изменчивость населения мелких млекопитающих и
демографической структуры их популяций в микромасштабе [презентация к выступлению на конференции]
Слайд 27Сравнение четырех выборок (линии 1- 4) (критерий Краскела-Уолиса) H (
Попарное сравнение выборок (тест Манна-Уитни) также не выявило статистически значимых (р<0.05) различий между ними.
Различия между выборками с линий 1-4 и 5 не значимы (тест Манна-Уитни) р=0.13, что может быть связано с малым размером выборки с линии 5.
N = 23 9 16 16 4
Удельная активность 90Sr в костной ткани
Microtus oeconomus
Модоров М.В., Селезнев А.А. Пространственно-временная изменчивость населения мелких млекопитающих и
демографической структуры их популяций в микромасштабе [презентация к выступлению на конференции]