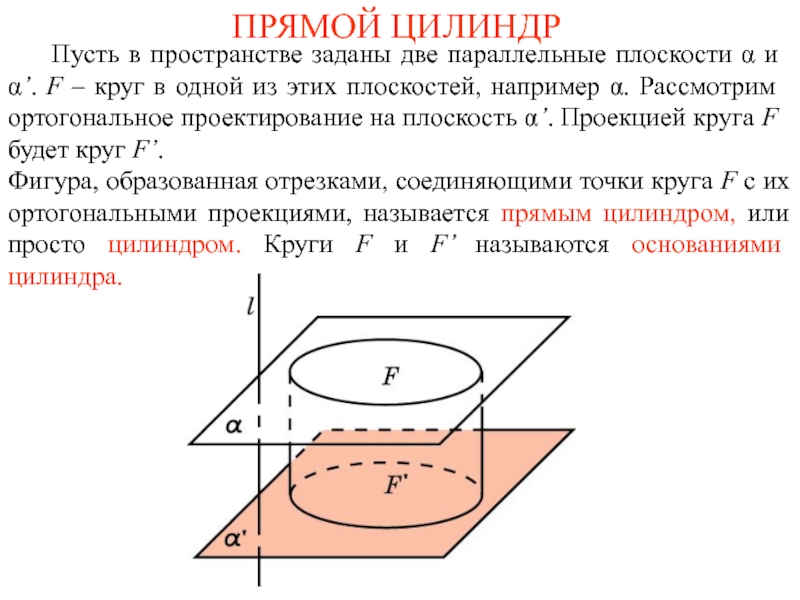
Фигура, образованная отрезками, соединяющими точки круга F с их ортогональными проекциями, называется прямым цилиндром, или просто цилиндром. Круги F и F’ называются основаниями цилиндра.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямой цилиндр презентация
Содержание
- 1. Прямой цилиндр
- 2. НАКЛОННЫЙ ЦИЛИНДР В случае, если вместо ортогонального
- 3. Боковая поверхность цилиндра Фигура,
- 4. ПРЯМОЙ И НАКЛОННЫЙ КОНУС
- 5. Боковая поверхность конуса Фигура,
- 6. УСЕЧЕННЫЙ КОНУС Если конус
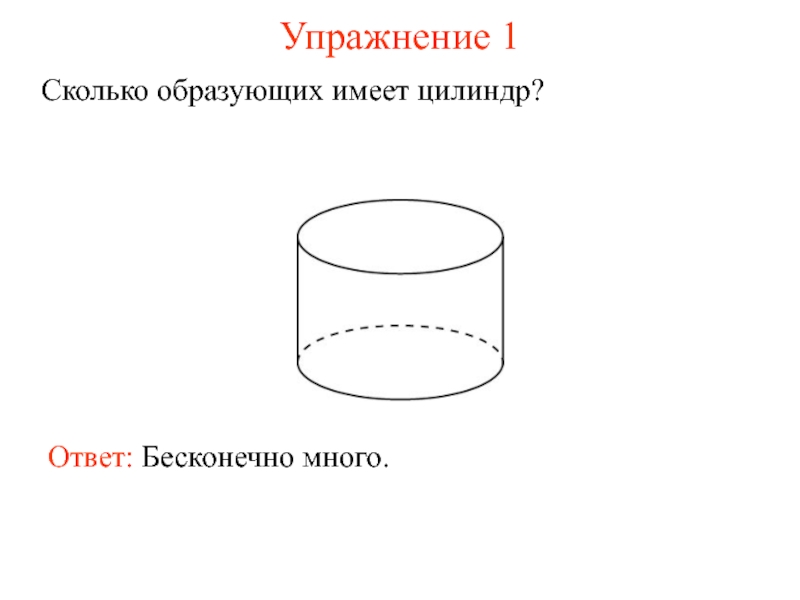
- 7. Упражнение 1 Сколько образующих имеет цилиндр? Ответ: Бесконечно много.
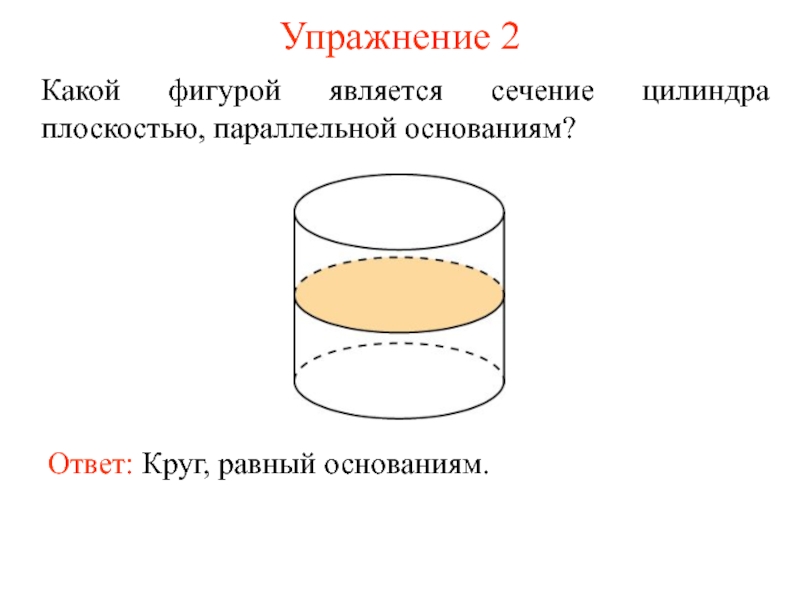
- 8. Упражнение 2 Какой фигурой является сечение цилиндра плоскостью, параллельной основаниям?
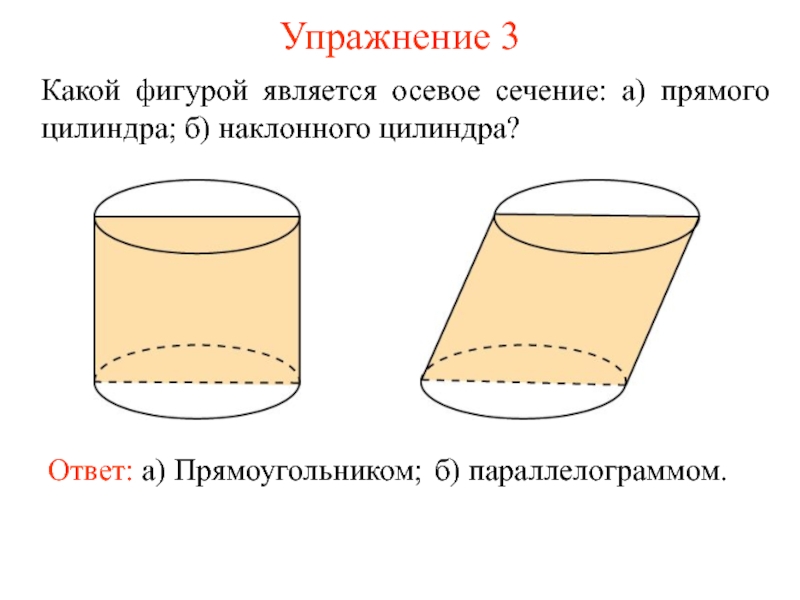
- 9. Упражнение 3 Какой фигурой является осевое сечение: а) прямого цилиндра; б) наклонного цилиндра?
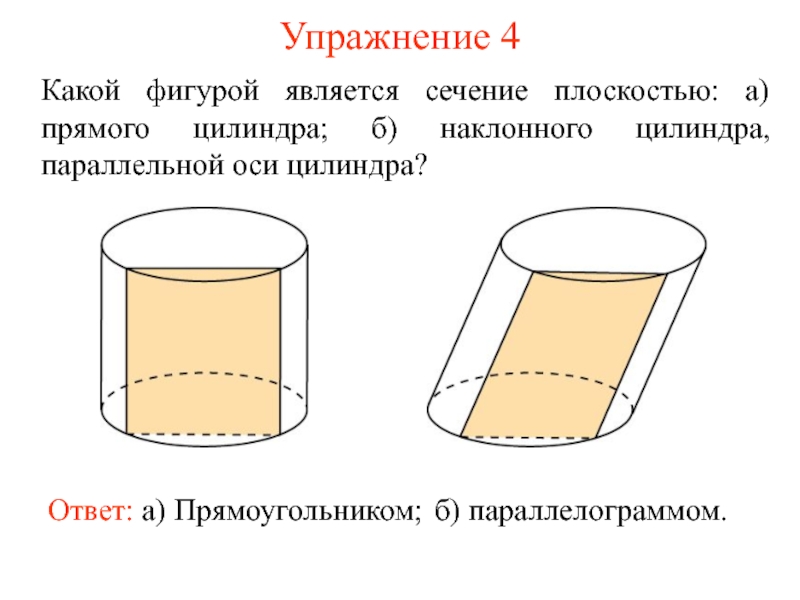
- 10. Упражнение 4 Какой фигурой является сечение плоскостью:
- 11. Упражнение 5 Радиус основания цилиндра равен 2
- 12. Упражнение 6 Осевым сечением цилиндра является квадрат,
- 13. Упражнение 7 Высота цилиндра 8 дм, радиус
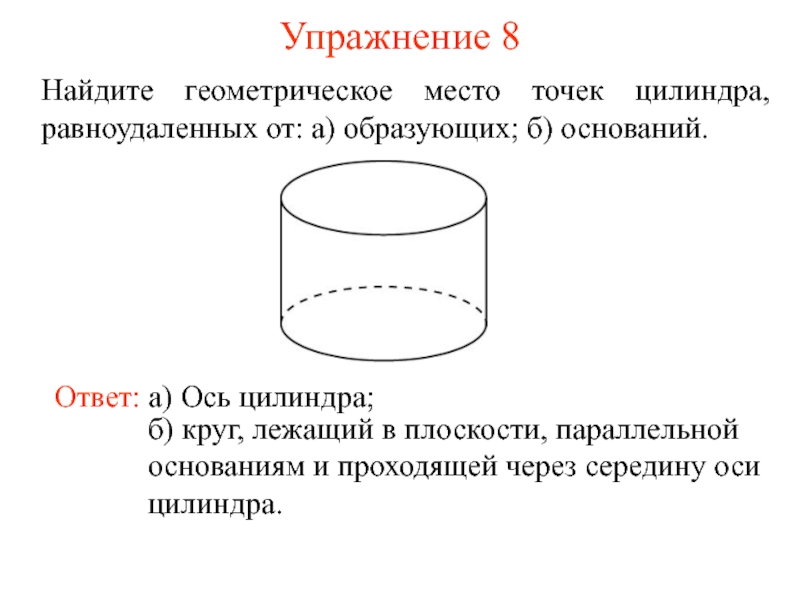
- 14. Упражнение 8 Найдите геометрическое место точек цилиндра,
- 15. Упражнение 9 Два цилиндра имеют две общие
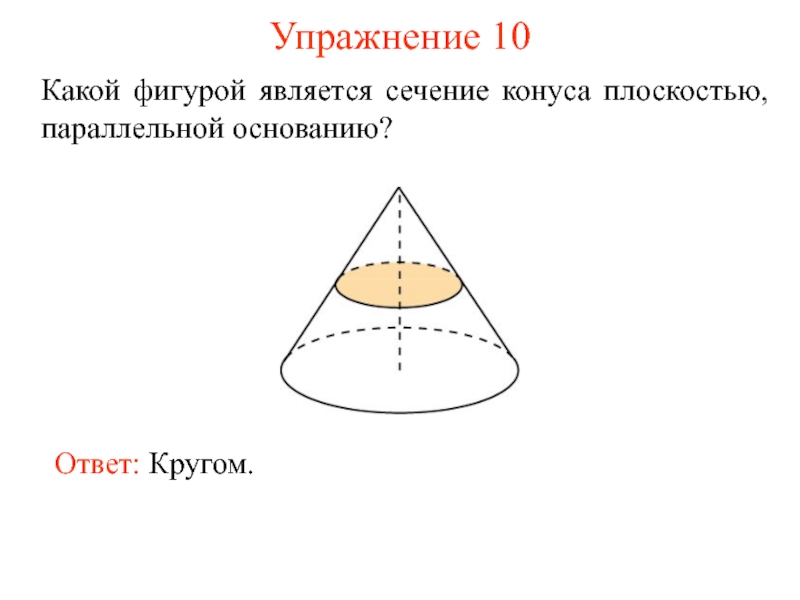
- 16. Упражнение 10 Какой фигурой является сечение конуса плоскостью, параллельной основанию?
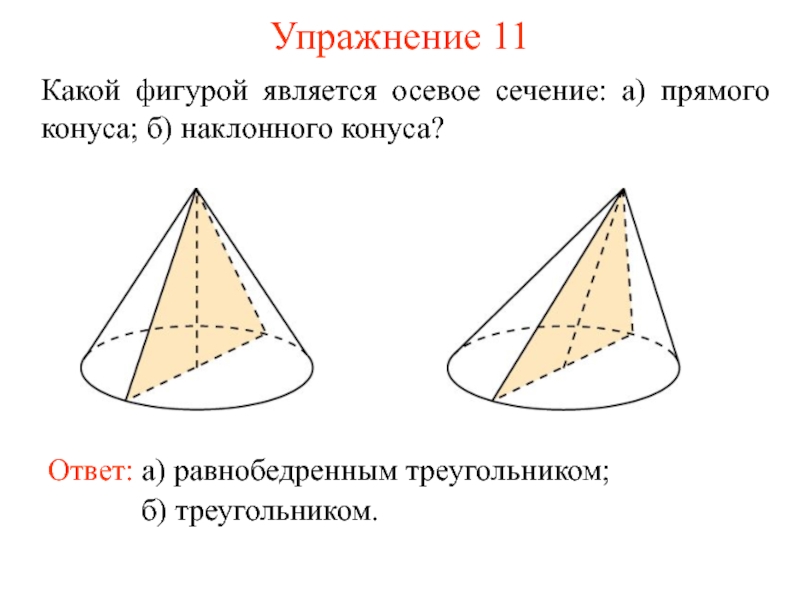
- 17. Упражнение 11 Какой фигурой является осевое сечение: а) прямого конуса; б) наклонного конуса?
- 18. Упражнение 12 Радиус основания конуса равен 4
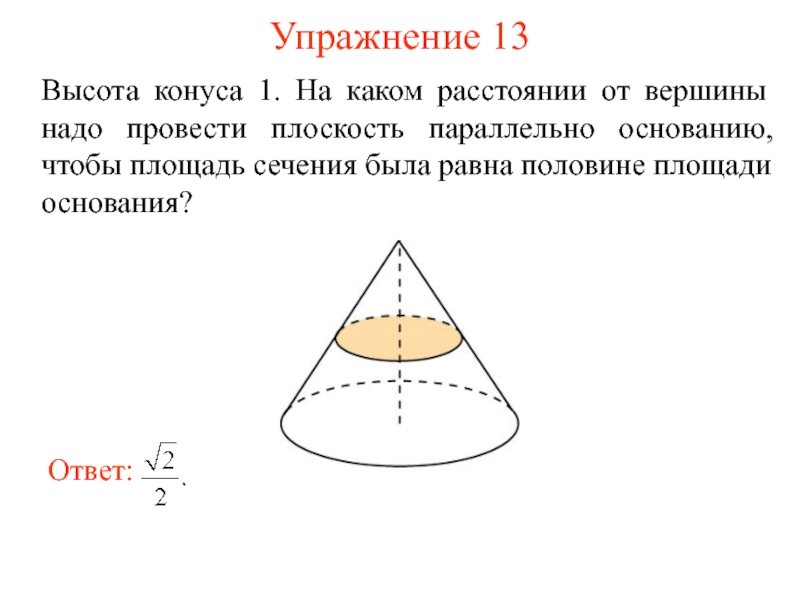
- 19. Упражнение 13 Высота конуса 1. На каком
- 20. Упражнение 14 Высота конуса равна 8 м,
- 21. Упражнение 15 Осевое сечение конуса - равносторонний
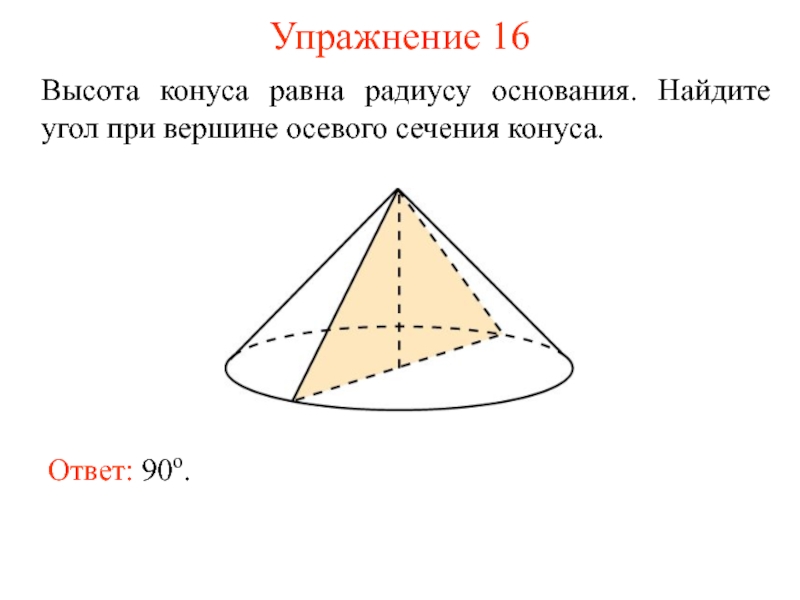
- 22. Упражнение 16 Высота конуса равна радиусу основания.
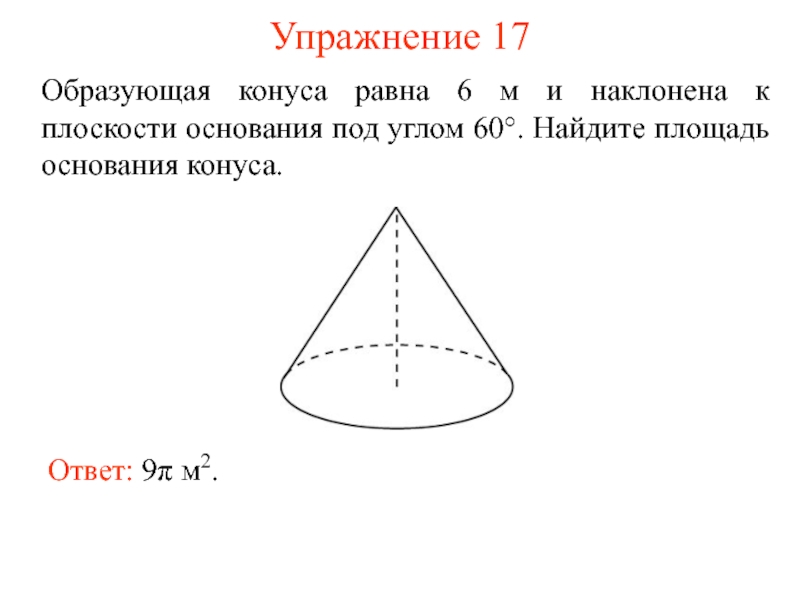
- 23. Упражнение 17 Образующая конуса равна 6 м
- 24. Упражнение 18 Найдите геометрическое место точек конуса,
- 25. Упражнение 19 Определите понятия прямого и наклонного
- 26. Упражнение 20 Какая фигура является осевым сечением
- 27. Упражнение 21 Радиусы оснований усеченного конуса равны
НАКЛОННЫЙ ЦИЛИНДР В случае, если вместо ортогонального проектирования берется параллельное проектирование в направлении наклонной к плоскости α’, то фигура, образованная отрезками, соединяющими точки круга F с их параллельными проекциями, называется наклонным
Слайд 1ПРЯМОЙ ЦИЛИНДР
Пусть в пространстве заданы две параллельные плоскости
α и α’. F – круг в одной из этих плоскостей, например α. Рассмотрим ортогональное проектирование на плоскость α’. Проекцией круга F будет круг F’.
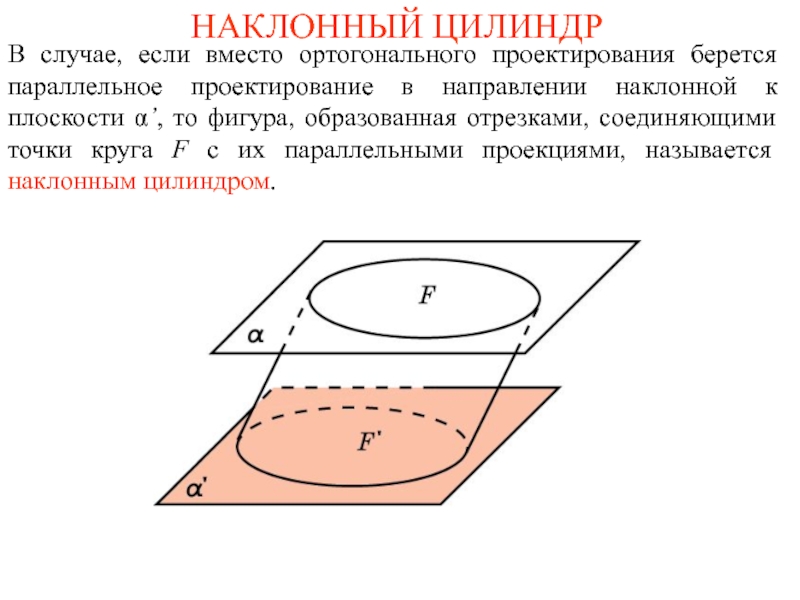
Слайд 2НАКЛОННЫЙ ЦИЛИНДР
В случае, если вместо ортогонального проектирования берется параллельное проектирование в
направлении наклонной к плоскости α’, то фигура, образованная отрезками, соединяющими точки круга F с их параллельными проекциями, называется наклонным цилиндром.
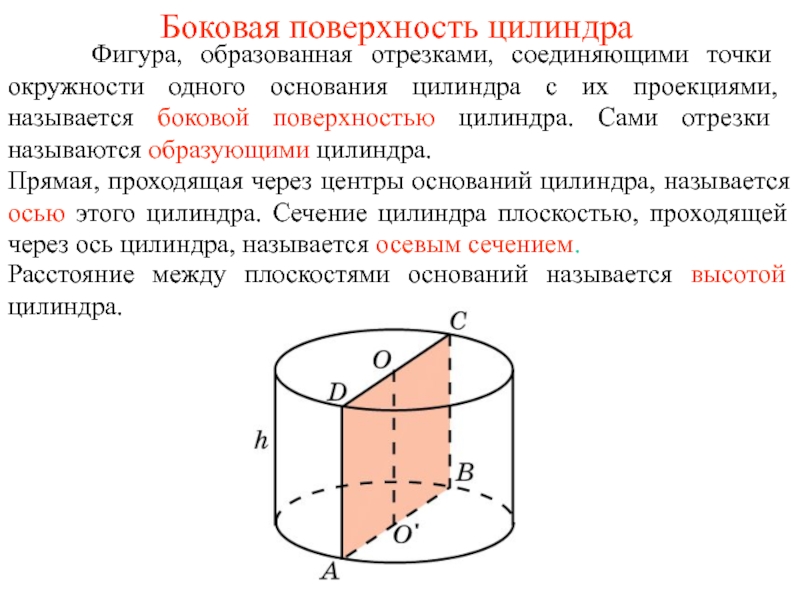
Слайд 3Боковая поверхность цилиндра
Фигура, образованная отрезками, соединяющими точки окружности
одного основания цилиндра с их проекциями, называется боковой поверхностью цилиндра. Сами отрезки называются образующими цилиндра.
Прямая, проходящая через центры оснований цилиндра, называется осью этого цилиндра. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Расстояние между плоскостями оснований называется высотой цилиндра.
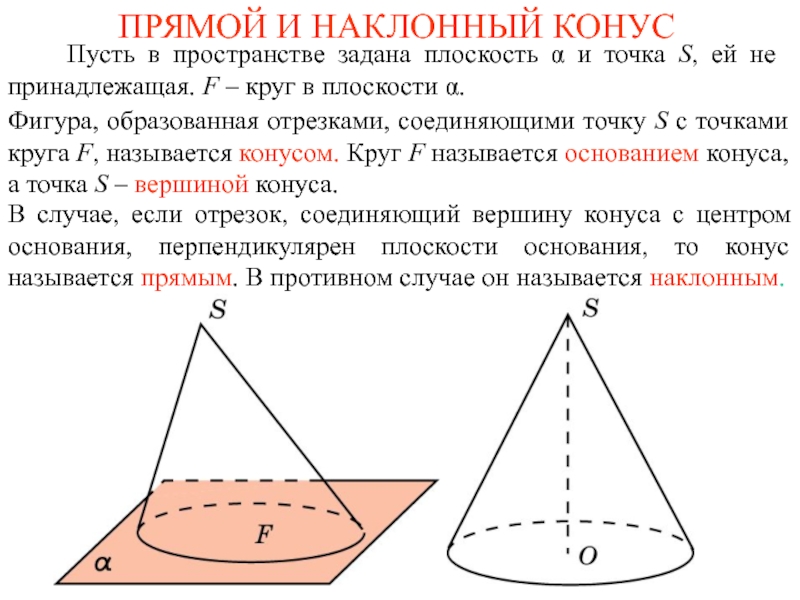
Слайд 4ПРЯМОЙ И НАКЛОННЫЙ КОНУС
Пусть в пространстве задана плоскость
α и точка S, ей не принадлежащая. F – круг в плоскости α.
Фигура, образованная отрезками, соединяющими точку S c точками круга F, называется конусом. Круг F называется основанием конуса, а точка S – вершиной конуса.
В случае, если отрезок, соединяющий вершину конуса с центром основания, перпендикулярен плоскости основания, то конус называется прямым. В противном случае он называется наклонным.
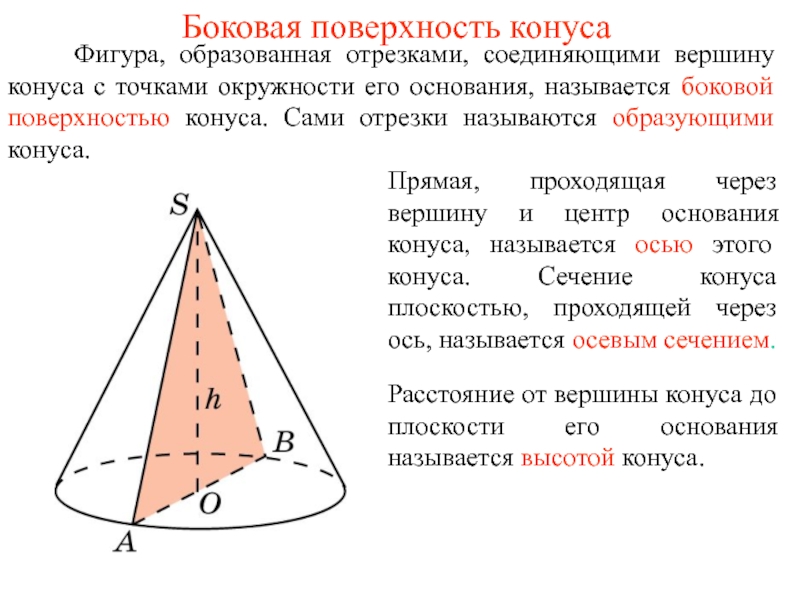
Слайд 5Боковая поверхность конуса
Фигура, образованная отрезками, соединяющими вершину конуса
с точками окружности его основания, называется боковой поверхностью конуса. Сами отрезки называются образующими конуса.
Прямая, проходящая через вершину и центр основания конуса, называется осью этого конуса. Сечение конуса плоскостью, проходящей через ось, называется осевым сечением.
Расстояние от вершины конуса до плоскости его основания называется высотой конуса.
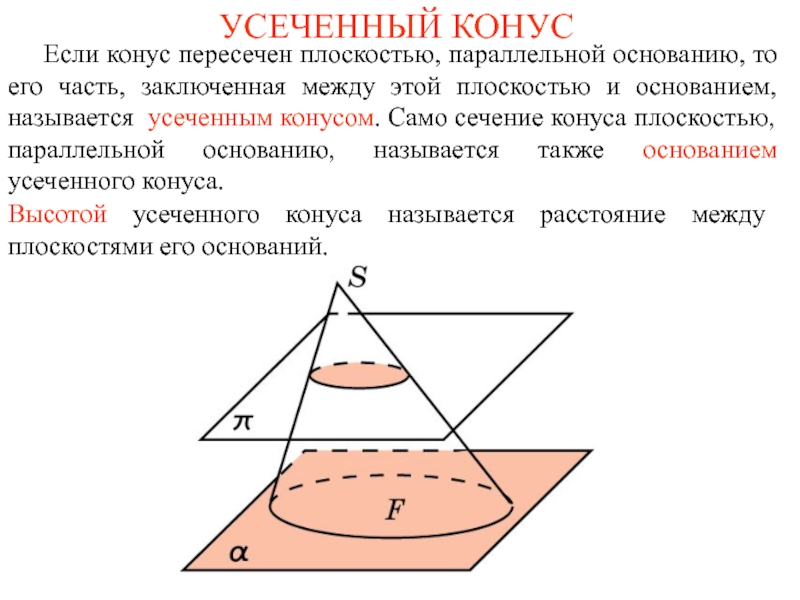
Слайд 6УСЕЧЕННЫЙ КОНУС
Если конус пересечен плоскостью, параллельной основанию, то
его часть, заключенная между этой плоскостью и основанием, называется усеченным конусом. Само сечение конуса плоскостью, параллельной основанию, называется также основанием усеченного конуса.
Высотой усеченного конуса называется расстояние между плоскостями его оснований.
Слайд 9Упражнение 3
Какой фигурой является осевое сечение: а) прямого цилиндра; б) наклонного
цилиндра?
Слайд 10Упражнение 4
Какой фигурой является сечение плоскостью: а) прямого цилиндра; б) наклонного
цилиндра, параллельной оси цилиндра?
Слайд 11Упражнение 5
Радиус основания цилиндра равен 2 м, высота - 3 м.
Найдите диагональ осевого сечения.
Ответ: 5 м.
Слайд 12Упражнение 6
Осевым сечением цилиндра является квадрат, площадь которого равна 4. Найдите
радиус основания цилиндра.
Ответ: 1.
Слайд 13Упражнение 7
Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен
плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси.
Ответ: 3 дм.
Слайд 14Упражнение 8
Найдите геометрическое место точек цилиндра, равноудаленных от: а) образующих; б)
оснований.
Ответ: а) Ось цилиндра;
б) круг, лежащий в плоскости, параллельной основаниям и проходящей через середину оси цилиндра.
Слайд 15Упражнение 9
Два цилиндра имеют две общие образующие. Какая фигура получится при
пересечении этих цилиндров плоскостью, перпендикулярной их осям?
Ответ: Два пересекающихся круга.
Слайд 17Упражнение 11
Какой фигурой является осевое сечение: а) прямого конуса; б) наклонного
конуса?
Слайд 18Упражнение 12
Радиус основания конуса равен 4 см. Осевым сечением служит прямоугольный
треугольник. Найдите его площадь.
Ответ: 16 см2.
Слайд 19Упражнение 13
Высота конуса 1. На каком расстоянии от вершины надо провести
плоскость параллельно основанию, чтобы площадь сечения была равна половине площади основания?
Слайд 20Упражнение 14
Высота конуса равна 8 м, радиус основания - 6 м.
Найдите образующую конуса.
Ответ: 10 м.
Слайд 21Упражнение 15
Осевое сечение конуса - равносторонний треугольник со стороной 10 см.
Найдите радиус основания и высоту конуса.
Слайд 22Упражнение 16
Высота конуса равна радиусу основания. Найдите угол при вершине осевого
сечения конуса.
Ответ: 90о.
Слайд 23Упражнение 17
Образующая конуса равна 6 м и наклонена к плоскости основания
под углом 60°. Найдите площадь основания конуса.
Ответ: 9π м2.
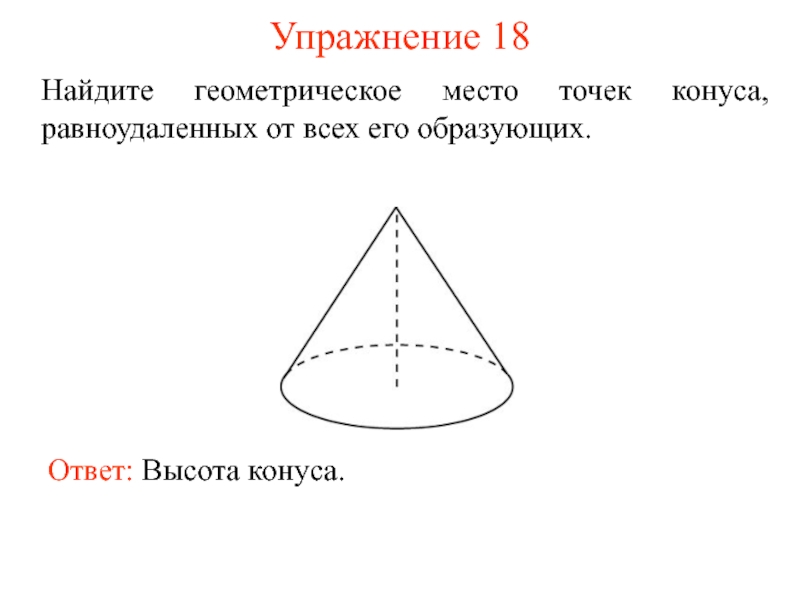
Слайд 24Упражнение 18
Найдите геометрическое место точек конуса, равноудаленных от всех его образующих.
Ответ:
Высота конуса.
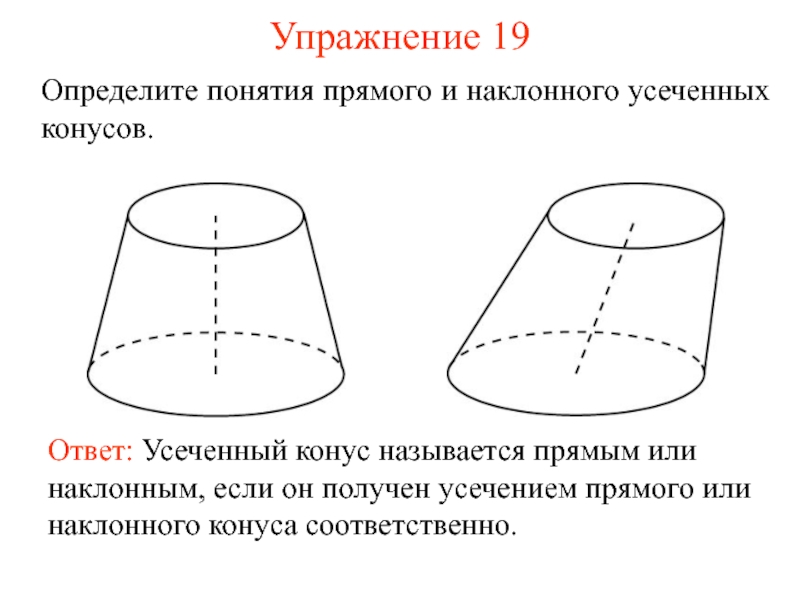
Слайд 25Упражнение 19
Определите понятия прямого и наклонного усеченных конусов.
Ответ: Усеченный конус называется
прямым или наклонным, если он получен усечением прямого или наклонного конуса соответственно.
Слайд 26Упражнение 20
Какая фигура является осевым сечением : а) прямого усеченного конуса;
б) наклонного усеченного конуса?
Слайд 27Упражнение 21
Радиусы оснований усеченного конуса равны 3 см и 6 см,
образующая – 5 см. Найдите высоту усеченного конуса.
Ответ: 4 см.
