Прямокутні координати в просторі презентация

Содержание

РЕНЕ ДЕКАРТ (1596--1650) ФіЛОСОФ, МАТЕМАТИК, ПРИРОДОДОСЛІДНИК Прямокутну систему координат СТВОРИВ х о у

Слайд 1
О




y





x
z
1
1
1
Прямокутні координати в просторі.

Слайд 2РЕНЕ ДЕКАРТ (1596--1650)
ФіЛОСОФ, МАТЕМАТИК, ПРИРОДОДОСЛІДНИК
Прямокутну систему координат
СТВОРИВ


х

о


у

Слайд 3


ВІДВІДУЮЧИ ПАРИЗЬКІ ТЕАТРИ, ДЕКАРТ НЕ ВТОМЛЮВАВСЯ ДИВУВАТИСЯ ПУТАНИНІ, СУПЕРЕЧКАМ, А ЧАСОМ

І ВИКЛИКАМ НА ДУЕЛЬ, ЯКІ ВИКЛИКАЛИСЯ ВІДСУТНІСТЮ ЕЛЕМЕНТАРНОГО ПОРЯДКУ РОЗПОДІЛУ ПУБЛІКИ В ЗАЛІ ДЛЯ ГЛЯДАЧІВ.
ВІН ЗАПРОПОНУВАВ СИСТЕМУ НУМЕРАЦІЇ, В ЯКІЙ КОЖНЕ МІСЦЕ ОТРИМУВАЛО НОМЕР РЯДУ І ПОРЯДКОВИЙ НОМЕР ВІД КРАЮ.
ВОНА ВІДРАЗУ ЗНЯЛА ВСІ ПРИВОДИ ДЛЯ СУПЕРЕЧОК І ВИКЛИКАЛА СПРАВЖНІЙ ФУРОР.
ЦЕЙ МЕТОД НУМЕРАЦІЇ КРІСЕЛ У ГЛЯДАЦЬКІЙ ЗАЛІ ПО РЯДАМ І МІСЦЯМ ЗБЕРЕЖЕНИЙ І СЬОГОДНІ.


у

№

Р
Я
Д
А

№ МІСЦЯ У РЯДІ

х

Слайд 4Питаннязаняття.
1. Скількома координатами може бути задана точка на прямій?
Однією.
2. Скількома

координатами задана точка в координатній площині?

Двома.

3. Скількома координатами задана точка у просторі?

ТРЬОМА

х


А ( )


х

у

А (х; у)

О

(0;0)


х

у

х

Слайд 5Задання прямокутної системи координат у просторі:




y
Оy Оz
Оz

Оx


Оy Оx





x

z

1

1

1

Ох – вісь абсцис

Оу – вісь ординат

Оz – вісь аплікат

О



Слайд 6

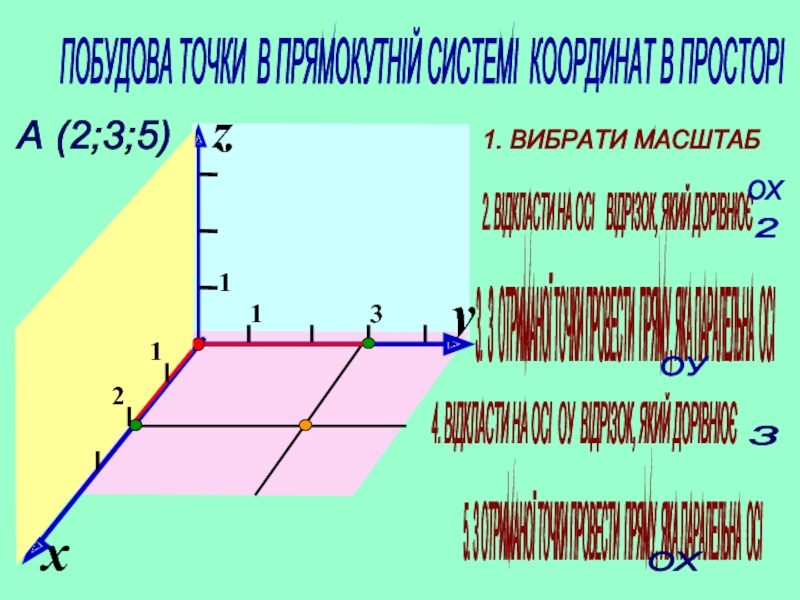
ПОБУДОВА ТОЧКИ В ПРЯМОКУТНІЙ СИСТЕМІ КООРДИНАТ В ПРОСТОРІ

y



x
1
1

z

А (2;3;5)
1.

ВИБРАТИ МАСШТАБ

2. ВІДКЛАСТИ НА ОСІ ВІДРІЗОК, ЯКИЙ ДОРІВНЮЄ

3. З ОТРИМАНОЇ ТОЧКИ ПРОВЕСТИ ПРЯМУ, ЯКА ПАРАЛЕЛЬНА ОСІ

4. ВІДКЛАСТИ НА ОСІ ОУ ВІДРІЗОК, ЯКИЙ ДОРІВНЮЄ


3

5. З ОТРИМАНОЇ ТОЧКИ ПРОВЕСТИ ПРЯМУ, ЯКА ПАРАЛЕЛЬНА ОСІ


ОХ

2

ОУ

ОХ

3

О



1

2

Слайд 7


y




x
1
1
1
О

z

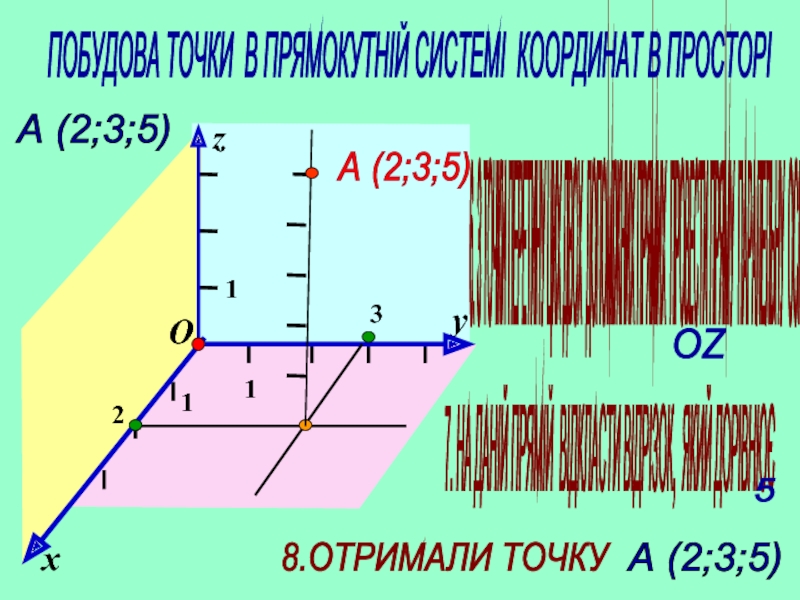
А (2;3;5)
2


3

6. З ТОЧКИ ПЕРЕТИНУ ЦИХ ДВОХ ДОПОМІЖНИХ ПРЯМИХ ПРОВЕСТИ

ПРЯМУ ПАРАЛЕЛЬНУ ОСІ

7. НА ДАНІЙ ПРЯМІЙ ВІДКЛАСТИ ВІДРІЗОК, ЯКИЙ ДОРІВНЮЄ







А (2;3;5)

ОZ

5

8.ОТРИМАЛИ ТОЧКУ

А (2;3;5)

ПОБУДОВА ТОЧКИ В ПРЯМОКУТНІЙ СИСТЕМІ КООРДИНАТ В ПРОСТОРІ

Слайд 8


Знахождення координат точок.
на осі
Оу
Ох
Оz









x
1
1
1
О

А (4;0;0)
В (0;0;3)
С

(0;4;0)

y

Точка лежить



(х; 0; 0)


(0; у; 0)


(0; 0; z)

z

А

( )

Х;

У;

Z

Слайд 9
Знахождення координат точок.
в координатной
плоскости
Оху (х; у; 0)




Охz (х; 0; z)
Оуz (0;

у; z)

Точка лежить







x

1

1

1

О


N (0;2;1)

М (2;3;0)

y



z

К (3;0;2)

К (3;0;2)


N (0;2;1)


М (2;3;0)

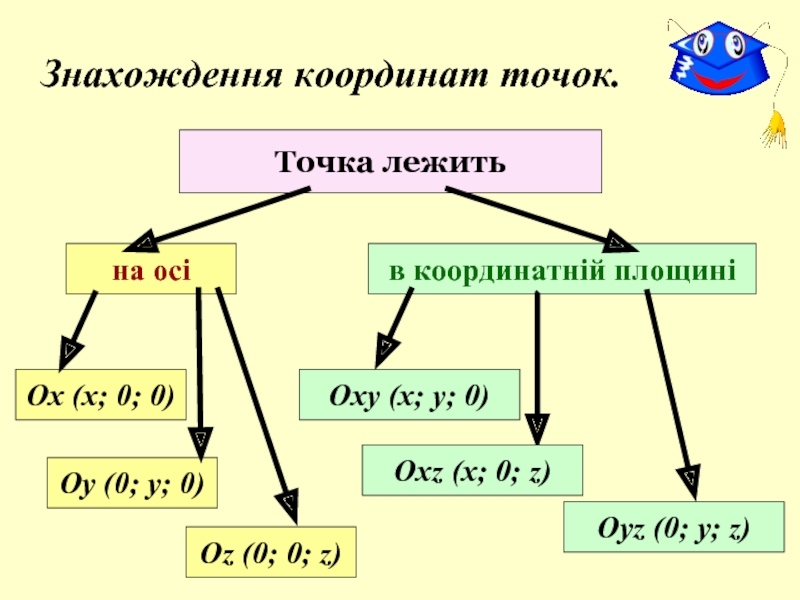
Слайд 10Знахождення координат точок.
Точка лежить
на осі
Оу (0; у; 0)
Ох (х; 0; 0)
Оz

(0; 0; z)

в координатній площині

Оху (х; у; 0)









Охz (х; 0; z)

Оуz (0; у; z)

Слайд 11



y





x
z
1
1
1
О




А (4;0;0)
Б (0;0;3)


С (0;4;0)
К (3;0;2)

М (2;3;0)

N

(0;2;1)

Розміщення координат точок

Слайд 12ПІД ЯКИМ КУТОМ
ПЕРЕТИНАЮТЬСЯ
КООРДИНАТНІ
ПРЯМІ
У ПРОСТОРІ:
ЯК НАЗИВАЮТЬ
ТОЧКУ ПЕРЕТИНУ
КООРДИНАТНИХ
ПРЯМИХ:
ЯК
НАЗИВАЮТЬСЯ
(Х; У; Z)
ДЛЯ

ТОЧКИ
У ПРОСТОРІ:

А) ПОЧАТОК ВСІХ
ПОЧАТКІВ;

Б) СЕРЕДИНА;

В) ПОЧАТОК
КООРДИНАТ;

Г) РОЗДІЛЬНИК

А)КООРДИНАТИ
ТОЧКИ;

Б)ЧИСЛА У ПРОСТОРІ;

В)ЧИСЛА ДЛЯ ТОЧКИ;

Г) ПОКАЗНИКИ ТОЧКИ

А) ПІД ОСТРИМ КУТОМ;

Б)ПІД ПРЯМИМ
КУТОМ;

В)ПІД ТУПИМ КУТОМ;

Г) ПІД РАЗГОРНУТИМ
КУТОМ

А) ПІД ОСТРИМ
КУТОМ;

Б) ПІД ПРЯМИМ
КУТОМ;

В) ПІД ТУПИМ КУТОМ;

Г) ПІД РАЗГОРНУТИМ
КУТОМ

А) ПОЧАТОК
ВСІХ
ПОЧАТКІВ;

Б) СЕРЕДИНА;

В) ПОЧАТОК
КООРДИНАТ;

Г) РОЗДІЛЬНИК

А) КООРДИНАТИ
ТОЧКИ;

Б) ЧИСЛА
У ПРОСТОРІ;

В) ЧИСЛА
ДЛЯ ТОЧКИ;

Г) ПОКАЗНИКИ
ТОЧКИ

Слайд 13ЯК
НАЗИВАЕТЬСЯ
ВІСЬ ОХ:
ЯК
НАЗИВАЕТЬСЯ
ВІСЬ ОУ:
ЯК
НАЗИВАЕТЬСЯ
ВІСЬ ОZ :
А)

ОРДИНАТА;

Б) АБСЦИСА;

В) БІСЕКТРИСА;

Г) АПЛІКАТА

А) АБСЦИСА;

Б) АПЛІКАТА;

В) ОРДИНАТА;

Г) БІСЕКТРИСА

А) АПЛІКАТА;

Б) ОРДИНАТА;

В) АБСЦИСА;

Г) БІСЕКТРИСА

А) АПЛІКАТА;

Б) ОРДИНАТА;

В) АБСЦИСА;

Г) БІСЕКТРИСА

А) ОРДИНАТА;

Б) АБСЦИСА;

В) БІСЕКТРИСА;

Г) АПЛІКАТА

А) АБСЦИСА;

Б) АПЛІКАТА;

В) ОРДИНАТА;

Г) БІСЕКТРИСА

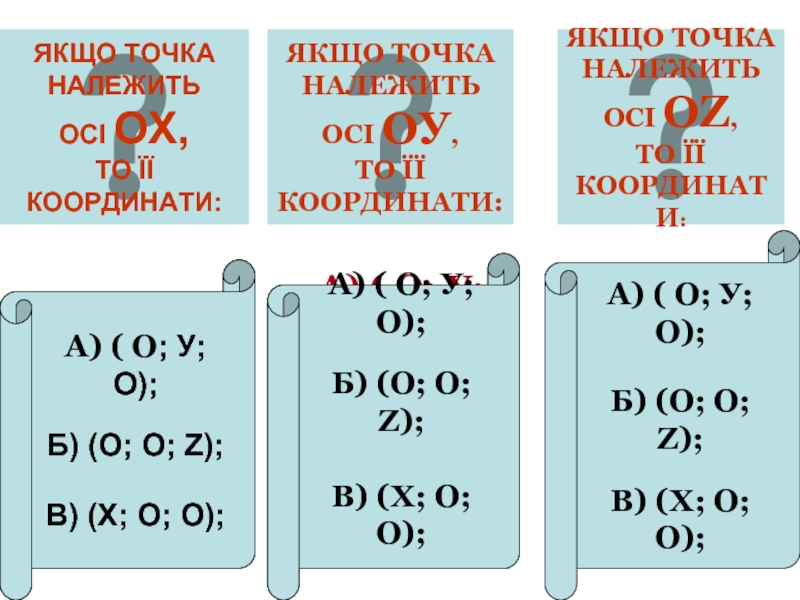
Слайд 14ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОСІ ОХ,
ТО ЇЇ
КООРДИНАТИ:
ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОСІ ОУ,
ТО ЇЇ
КООРДИНАТИ:
ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОСІ ОZ,
ТО

ЇЇ
КООРДИНАТИ:

А) ( О; У; О);

Б) (О; О; Z);

В) (Х; О; О);

А) ( О; У; О);

Б) (О; О; Z);

В) (Х; О; О);


А) ( О; У; О);

Б) (О; О; Z);

В) (Х; О; О);




А) ( О; У; О);

Б) (О; О; Z);

В) (Х; О; О);


А) ( О; У; О);

Б) (О; О; Z);

В) (Х; О; О);

А) ( О; У; О);

Б) (О; О; Z);

В) (Х; О; О);

Слайд 15


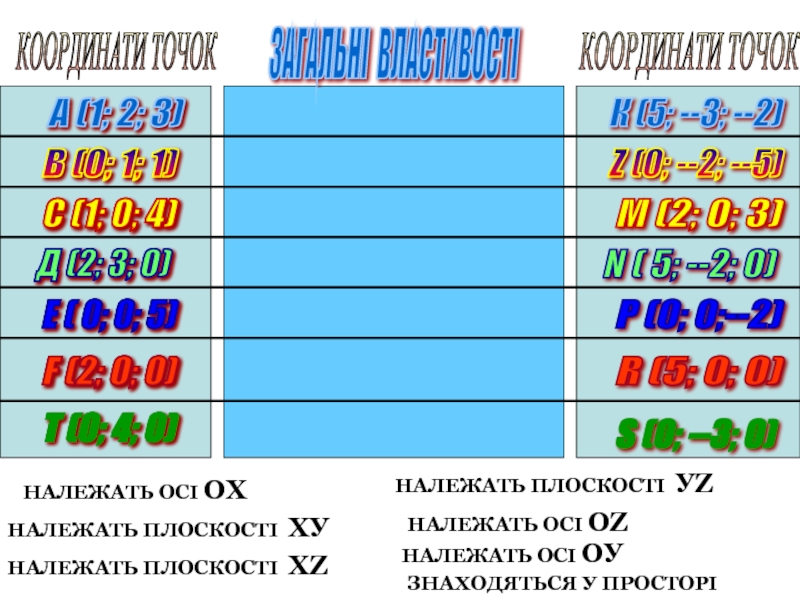
КООРДИНАТИ ТОЧОК
КООРДИНАТИ ТОЧОК
ЗАГАЛЬНІ ВЛАСТИВОСТІ
ЗНАХОДЯТЬСЯ У ПРОСТОРІ
НАЛЕЖАТЬ ПЛОСКОСТІ ХУ
НАЛЕЖАТЬ

ОСІ ОХ

А (1; 2; 3)

К (5; --3; --2)

В (0; 1; 1)

С (1; 0; 4)

Д (2; 3; 0)

Е ( 0; 0; 5)

F (2; 0; 0)

Т (0; 4; 0)

Z (0; --2; --5)

М (2; 0; 3)

N ( 5; --2; 0)

Р (0; 0;--2)

R (5; 0; 0)

S (0; --3; 0)

НАЛЕЖАТЬ ПЛОСКОСТІ ХZ

НАЛЕЖАТЬ ПЛОСКОСТІ УZ

НАЛЕЖАТЬ ОСІ ОУ

НАЛЕЖАТЬ ОСІ ОZ

А (1; 2; 3)

В (0; 1; 1)

С (1; 0; 4)

Д (2; 3; 0)

Е ( 0; 0; 5)

F (2; 0; 0)

Т (0; 4; 0)

НАЛЕЖАТЬ ОСІ ОХ

НАЛЕЖАТЬ ПЛОСКОСТІ ХУ

НАЛЕЖАТЬ ПЛОСКОСТІ ХZ

НАЛЕЖАТЬ ПЛОСКОСТІ УZ

НАЛЕЖАТЬ ОСІ ОZ

НАЛЕЖАТЬ ОСІ ОУ

ЗНАХОДЯТЬСЯ У ПРОСТОРІ

Слайд 16
ЗГАДАЕМО
ПЛАНІМЕТРІЮ


A
В
С

2
8
2
+
ЗНАЙТИ КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА:

А (2); В (8)

2

+

= 5

КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА

На координатній прямій

Слайд 17
Дані точки: А ( - 1; 7 )
а) Знайдіть координати

середини відрізка АВ.

A

В


х

о

у


С


и В ( 7; 1).


ЗГАДАЕМО

ПЛАНІМЕТРІЮ

--1

7

2

1

7

2

С

( 3;

4)

+

+

На координатній площині

КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА

А ( )

;

В ( )

;

С ( )

;

Слайд 18

У ПРОСТОРІ
КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА
А (

)

;

В ( )

;

С ( )

;

A


В


х

у

С


z


;

;

;


2

+

2

+


Слайд 19



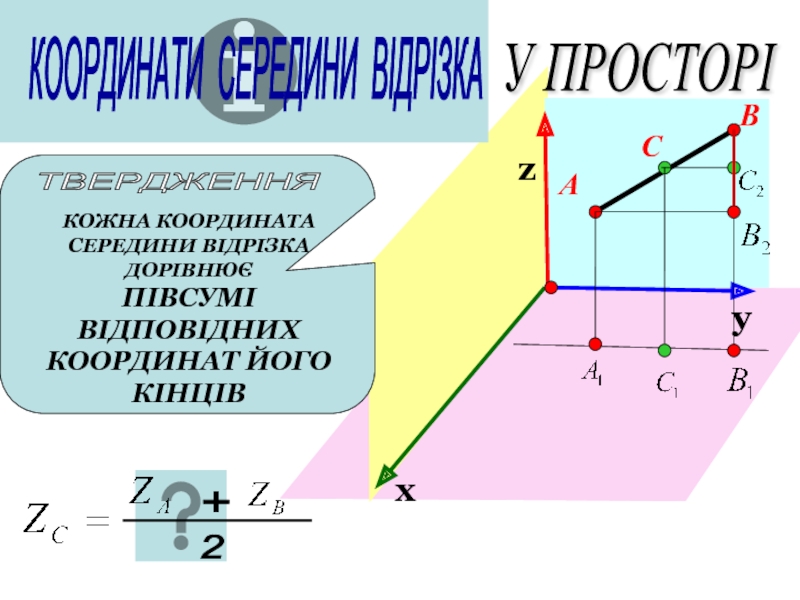
У ПРОСТОРІ
КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА
х
у

z



ТВЕРДЖЕННЯ
КОЖНА КООРДИНАТА СЕРЕДИНИ ВІДРІЗКА ДОРІВНЮЄ


ПІВСУМІ ВІДПОВІДНИХ КООРДИНАТ ЙОГО КІНЦІВ

A

В




С












2

+

Слайд 20

У ПРОСТОРІ
КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА
A

В

х
у
С

z


--1
7
2
+
1
7


2

+

4

2

2

+

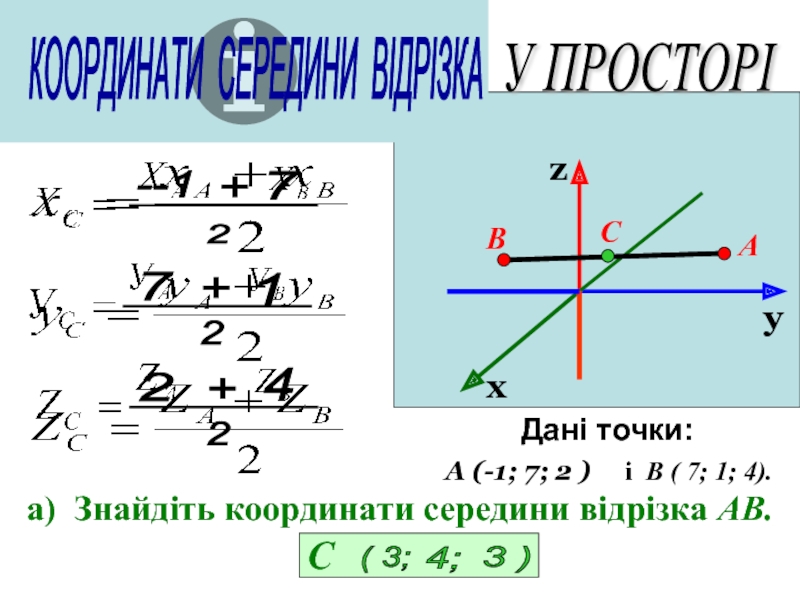
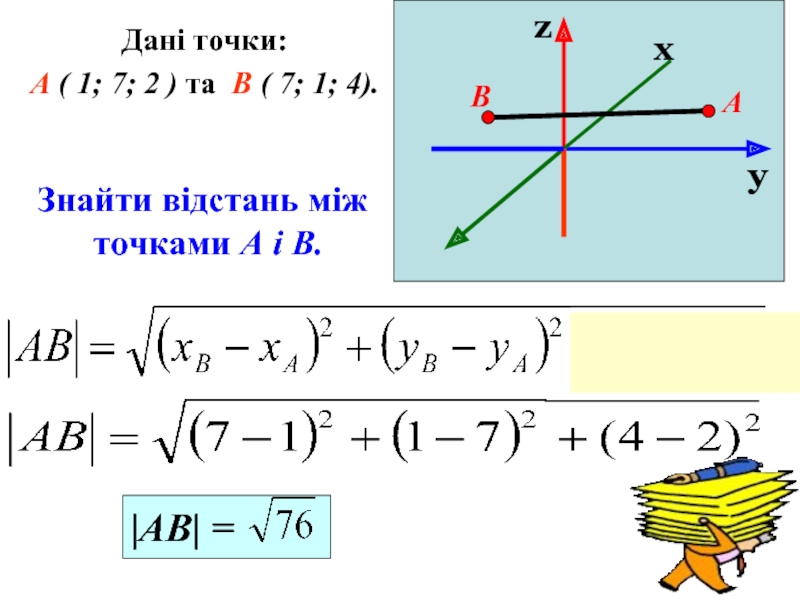
Дані точки:

і В ( 7; 1; 4).

а) Знайдіть координати середини відрізка АВ.

А (-1; 7; 2 )

С

( 3;

4;

3 )

Слайд 21
Дані точки: А ( - 1; 7 )



|АВ| = 10
A
В

х
о
у
ПРЯМОКУТНА

СИСТЕМА КООРДИНАТ НА ПЛОЩИНІ


та В ( 7; 1).


ЗГАДАЕМО

ПЛАНІМЕТРІЮ

Знайти відстань між двома точками
на площині

7

(-1)

1

7

Слайд 22



У ПРОСТОРІ
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ
х
у

z


ТВЕРДЖЕННЯ
КВАДРАТ ВІДСТАНІ
МІЖ ДВОМА ТОЧКАМИ
ДОРІВНЮЄ

СУМІ КВАДРАТІВ РІЗНИЦЬ
ЇХ ВІДПОВІДНИХ КООРДИНАТ










С







АВ

=

Слайд 23
Дані точки:
А ( 1; 7; 2 ) та В (

7; 1; 4).


A


В


х

у


z

Знайти відстань між точками А і В.

|АВ| =



Слайд 24

A
В
С

НА КООРДИНАТНІЙ ПРЯМІЙ
КООРДИНАТИ СЕРЕДИНИ
ВІДРІЗКА
ВІДСТАНЬ МІЖ
ДВОМА ТОЧКАМИ

A
В
х
о
у

С


НА КООРДИНАТНІЙ

ПЛОЩИНІ

У ПРОСТОРІ

х

у

z






Координати середини відрізка, якщо точки належать координатній прямій

?


Координати середини відрізка, якщо точки лежать у координатній площині

?


Координати середини відрізка, якщо точки лежать у просторі

?


Відстань між двома точками, якщо точки належать координатній прямій

?


Відстань між двома точками, якщо точки лежать у координатній площині

?


Відстань між двома точками, якщо точки лежать у просторі

?

Слайд 25МОЛОДЦІ!

Похожие презентации

zadachi na nahozhdenie summy 253
Матрица размера m x n 411
matematika 251
Статистическое определение вероятности 892
Случайные события. Вероятностное пространство 393
Решение задач С4. Планиметрия 1513

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика