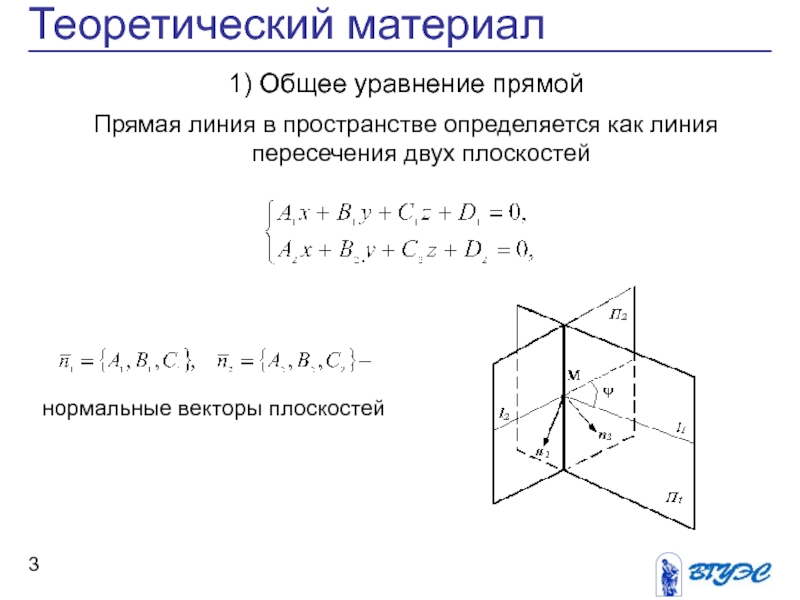
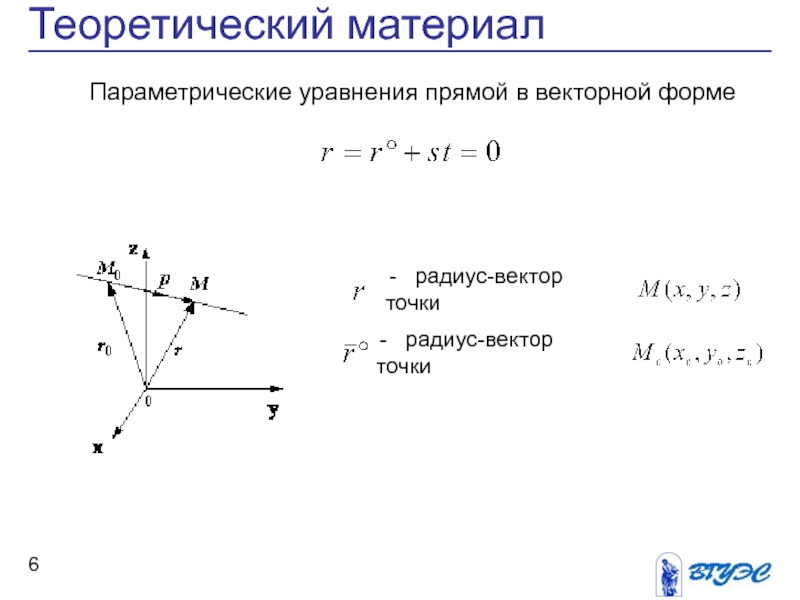
Переход от общих уравнений прямой к каноническому виду, векторное и параметрические уравнения прямой.
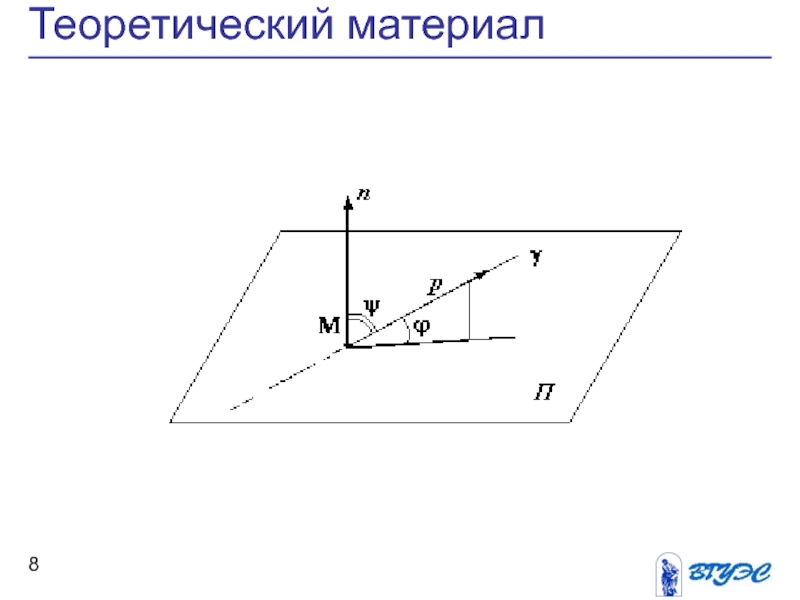
Уравнение прямой, проходящей через две заданные точки. Угол между двумя прямыми, условие параллельности и перпендикулярности. Взаимное расположение прямой и плоскости в пространстве: нахождение точки пересечения прямой и плоскости, условия параллельности и перпендикулярности.
- направляющий вектор прямой
4) Параметрические уравнения прямой
- радиус-вектор точки
.
Координаты точки пересечения находятся по формулам
подстановкой значения параметра
Прямые совпадают
.
или
В противном случае прямые являются скрещивающимися
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
