- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка статистических гипотез презентация
Содержание
- 1. Проверка статистических гипотез
- 2. Практическая работа №3
- 3. Основные понятия Статистическая гипотеза – это
- 4. Основные понятия Проверяемую гипотезу обычно называют нулевой
- 5. Основные понятия Решение – принять или отвергнуть
- 6. Принцип проверки статистических гипотез Реализация принципа: Задать
- 7. Критическая область Множество значений статистики Z, при
- 8. Критическая область В зависимости от вида конкурирующей
- 9. Область принятия решения Множество значений статистики
- 10. Критерий, основанный на использовании заранее заданного
- 11. Ошибки первого и второго рода Уровень значимости
- 12. Ошибки первого и второго рода
- 13. Ошибки первого и второго рода Статистическая ошибка
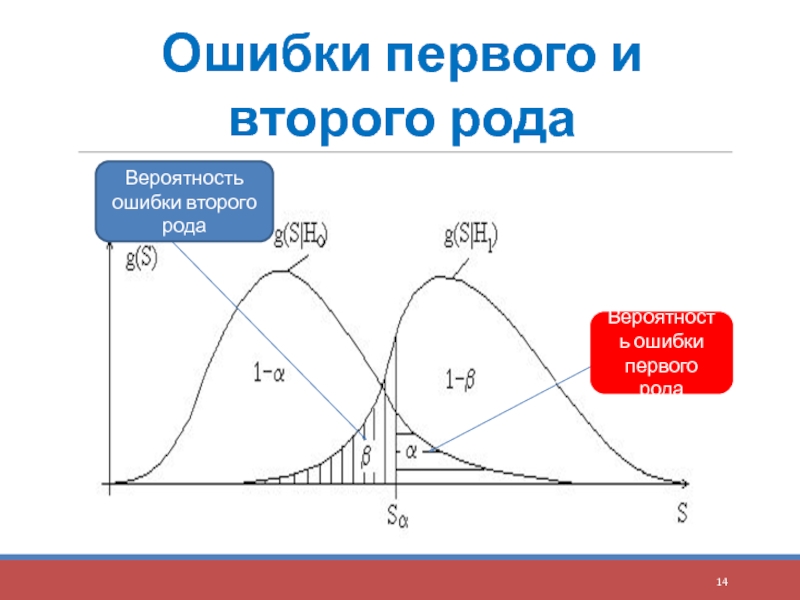
- 14. Ошибки первого и второго рода Вероятность ошибки первого рода Вероятность ошибки второго рода
- 15. Этапы проверки гипотезы о параметрах распределения 1.
- 16. Статистическое решение Если zв принадлежит критической области
- 17. Замечания 1. На этапах 4-7 используют статистику,
- 18. Пример 1 Сб. задач по математике для
- 19. Пример 2 В условиях примера 1 предположим,
- 20. Критерии согласия Пусть х1 , х2 …..
- 21. Критерий 4. Используя предполагаемый закон
- 22. Критерий 6. Гипотеза Н0 согласуется с результатами наблюдений на уровне значимости , если
- 23. Проверить гипотезу: Н0 : а = а0, где а0 = +0,5s
- 25. Проверить гипотезу: Н0 : = ϭ02
- 26. Критерий Объем выборки n=50. Оценка
- 27. pk =P[X Δк ]=Ф()-Ф()
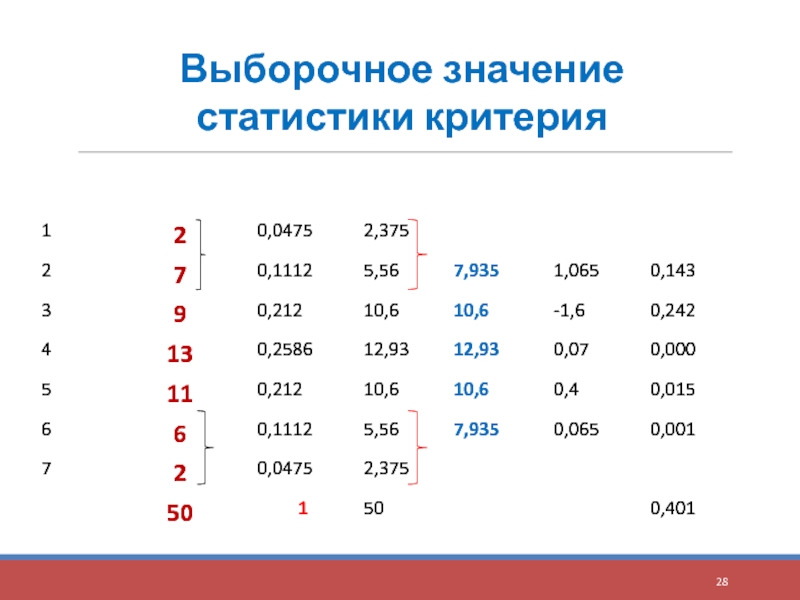
- 28. Выборочное значение статистики критерия
- 29. Статистическое решение Гипотеза Н0 согласуется с результатами наблюдений на уровне значимости , если
Слайд 3 Основные понятия
Статистическая гипотеза – это предположение о значении параметров закона
Статистическая гипотеза называется простой, если она однозначно определяет распределение с.в. Х; в противном случае, гипотеза называется сложной.
Слайд 4Основные понятия
Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают Н0.
Наряду с нулевой гипотезой рассматривают альтернативную (или конкурирующую) гипотезу Н1, являющуюся логическим отрицанием Н0.
Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Проверка статистической гипотезы H состоит в выяснении того, насколько эта гипотеза согласуется с опытными данными X.
Слайд 5Основные понятия
Решение – принять или отвергнуть гипотезу Н0 – принимается на
Правило, по которому принимается решение принять или отклонить гипотезу Н0, называется критерием К.
Принцип проверки статистических гипотез: маловероятные события считаются невозможными, а события, имеющие большую вероятность – достоверными.
Слайд 6Принцип проверки статистических гипотез
Реализация принципа:
Задать уровень значимости α.
Выбрать статистику Z критерия
Множество значений статистики Z разбить на непересекающиеся подмножества – критическую область и область принятия гипотезы Н0.
Слайд 7Критическая область
Множество значений статистики Z, при которых принимается решение отклонить гипотезу
Графически эта область определяется по кривой распределения.
Уровень значимости α определяет «размер» критической области
Критическая область выбирается так, чтобы вероятность попадания в нее была минимальной (равной α), если верна нулевая гипотеза Н0, и максимальной в противоположном случае.
Слайд 8Критическая область
В зависимости от вида конкурирующей гипотезы и распределения критерия выбирают
Границы (критические точки) при заданном уровне значимости находят из соотношений для критических областей:
правосторонней: P(Z > Zкр) = α;
левосторонней: P(Z < Zкр) = α;
двусторонней: P(Z < Zкр) = α /2 и P(Z > Zкр) = α /2.
Слайд 9Область принятия решения
Множество значений статистики Z, при которых гипотеза Н0
Слайд 10
Критерий, основанный на использовании заранее заданного уровня значимости α, называют критерием
Проверка статистических гипотез может быть проведена на основе соответствующих доверительных интервалов.
Слайд 11Ошибки первого и второго рода
Уровень значимости α – это вероятность ошибки
Значение α устанавливается на основе практического опыта в различных областях исследования. Вероятность α задается заранее малым числом: 0,05; 0,01; 0,005; 0,001.
Вероятность ошибки второго рода обозначают β – это вероятность того, что будет принята гипотеза Н0, если на самом деле верна гипотеза Н1.
Вероятность не совершить ошибку второго рода (1 – β), т. е. вероятность правильного отклонения неверной нулевой гипотезы, называют мощностью критерия.
Слайд 13Ошибки первого и второго рода
Статистическая ошибка первого рода (Type I Error)
Статистическая ошибка второго рода (Type II Error) - не обнаружить различия или связи, которые на самом деле существуют
«Судебная» аналогия: Вердикт «Не виновен» или «Виновен»
Ошибка первого рода - невинный обвинен
Ошибка второго рода - виновный освобожден
Слайд 15Этапы проверки гипотезы о параметрах распределения
1. формулируются гипотезы Н0 и Н1;
2.
3. выбирается статистика Z критерия для проверки Н0; определяется выборочное распределение статистики Z при условии, что верна Н0;
4. в зависимости от Н1 определяется критическая область;
5. вычисляется выборочное значение статистики z;
6. принимается статистическое решение.
Слайд 16Статистическое решение
Если zв принадлежит критической области
Отклонить гипотезу Н0 как несогласующуюся
Если zв не принадлежит критической области
Принять гипотезу Н0, т.е. считать, что она не противоречит результатам наблюдений
Слайд 17Замечания
1. На этапах 4-7 используют статистику, квантили которой табулированы.
2. В статистических
Эта вероятность называется р-значением (p-level).
Слайд 18Пример 1 Сб. задач по математике для втузов. Ч. 3. Теория вероятностей
По паспортным данным автомобильного двигателя расход топлива на 100 км. пробега составляет 10л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км. пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним а и дисперсией 4 л2 . Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
Слайд 19Пример 2
В условиях примера 1 предположим, что наряду с гипотезой Н0
Слайд 20Критерии согласия
Пусть х1 , х2 ….. хn– выборка наблюдений случайной величины
Проверяется гипотеза Н0 о том, что случайная величина X имеет функцию распределения F(x).
1. По выборке наблюдений находят оценки неизвестных параметров предполагаемого закона распределения с.в. Х.
2. Область возможных значений с.в. Х разбивается на r множеств Δ1, Δ2,… Δr . Если Х-непрерывная с.в., то на r интервалов, если Х-дискретная с.в., то r-число групп.
3. Подсчитывается число элементов выборки - nk, принадлежащих множеству Δк , к=1,2, ….r. =n.
Слайд 21Критерий
4. Используя предполагаемый закон распределения с.в. Х, находят вероятности pk
5. Выборочное значение статистики критерия вычисляется по формуле
Слайд 22Критерий
6. Гипотеза Н0 согласуется с результатами наблюдений на уровне значимости
где (r-l-1) – квантиль порядка 1-α распределения с (r-l-1) степенями свободы, l – число неизвестных параметров распределения, оцениваемых по выборке.
Необходимо, чтобы для всех интервалов выполнялось условие 5.
Если для некоторых интервалов это условие не выполняется, то их следует объединить с соседними.
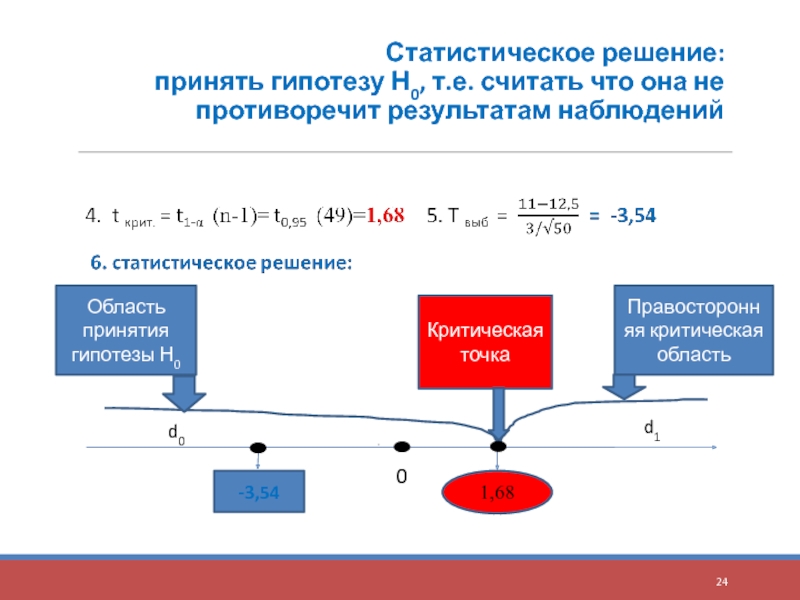
Слайд 24 Статистическое решение: принять гипотезу Н0, т.е. считать что она не противоречит
1,68
-3,54
Область принятия гипотезы Н0
Критическая точка
Правосторонняя критическая область
d1
d0
0
Слайд 25Проверить гипотезу:
Н0 : = ϭ02 , где ϭ02 = 3s
32,4
71,4
d0
d1
d1
Статистическое
Слайд 26Критерий
Объем выборки n=50.
Оценка математического ожидания =11
Оценка дисперсии S2 = 8,82
1. Н0 : Х распределена по нормальному закону
2. уровень значимости α=0,05
3.
Слайд 29Статистическое решение
Гипотеза Н0 согласуется с результатами наблюдений на уровне значимости ,
где (r-l-1) – квантиль порядка 1-α распределения с (r-l-1) степенями свободы, l – число неизвестных параметров распределения, оцениваемых по выборке.
r=5; l=2
Число степеней свободы r-l-1 = 5-2-1=2
(r-l-1)= (2) =(2)=5,99
= 0,401
Гипотеза о нормальном распределении выборки согласуется с результатами наблюдений



















![Критерий 4. Используя предполагаемый закон распределения с.в. Х, находят вероятности pk =P[X Δк ], к=1,2,](/img/tmb/4/365974/ee49f482085434fd697b5cc44ed929c4-800x.jpg)




![pk =P[X Δк ]=Ф()-Ф()](/img/tmb/4/365974/0da846d714117558e9634a564e9fb968-800x.jpg)