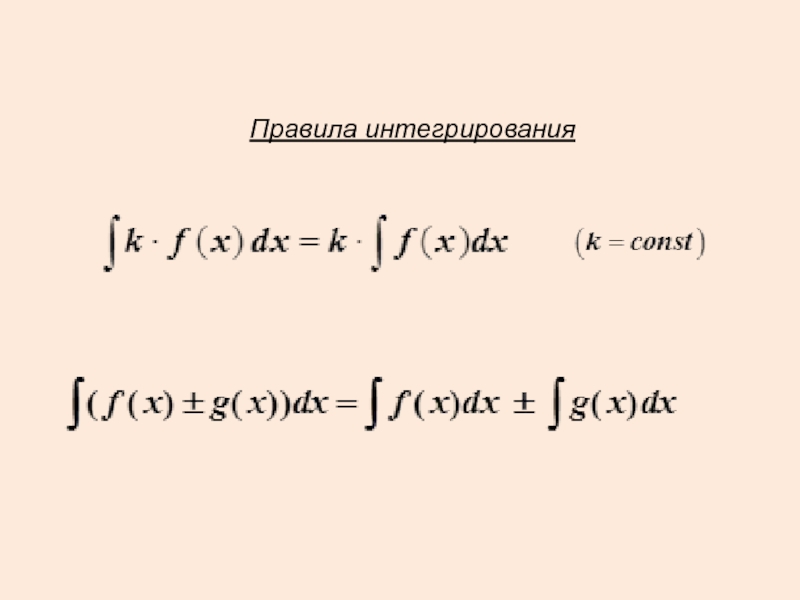Демонстрационный материал (учебно-наглядное пособие)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика. Демонстрационный материал (учебно-наглядное пособие) презентация
Содержание
- 1. Математика. Демонстрационный материал (учебно-наглядное пособие)
- 2. Введение Математика — фундаментальная наука, предоставляющая (общие)
- 3. Элементы теории матриц
- 4. Сумма (разность) двух матриц и
- 5. Произведением матрицы A из m строк
- 6. Пример. В частности,
- 7. Правило Крамера и определители матриц 2-го
- 8. Определитель третьего порядка обозначается
- 9. Решение системы трех уравнений с тремя
- 10. Вектор – это направленный отрезок. Обозначается вектор
- 11. Линейные операции над векторами Произведением
- 12. Суммой двух векторов и
- 13. Базисом
- 14. Декартовой прямоугольной системой координат называется совокупность
- 15. Радиус-вектором произвольной точки М называют вектор
- 16. Скалярное произведение Скалярным произведением векторов
- 17. С помощью скалярного произведения можно вычислить угол
- 18. Прямая линия на плоскости Общее уравнение
- 19. Уравнение прямой с угловым коэффициентом
- 20. Уравнение прямой, проходящей через две заданные точки
- 21. Пример 1. Составить общее уравнение
- 22. Пример 2. Найти угол между прямыми, заданными
- 23. Пример 3. Написать уравнение прямой, которая проходит
- 24. Элементы математического анализа Пусть заданы два множества
- 25. Предел функции — одно из основных понятий
- 26.
- 27. Дифференцирование Производная (функции в точке) —
- 28. Вычисление производных Правила дифференцирования: Производная
- 29. Постоянный множитель при дифференцировании выносится
- 30. Таблица основных производных
- 31. Производная сложной функции по независимой переменной равна
- 32.
- 33. Пример. Найти экстремумы функции
- 34. Интегрирование Функция F(x) называется первообразной для функции
- 35. Правила интегрирования
- 36. Таблица интегралов
- 37. Пример. Найти интеграл
- 38. Интегрирование методами подстановки и замены переменной.
- 39.
- 40. Формула интегрирования по частям
- 41. Определённым интегралом функции на промежутке
- 42. Формула Ньютона – Лейбница вычисления определенного интеграла:
- 43. Пример. Найти площадь фигуры, ограниченной линией
- 44. Правило замены переменной в определённом интеграле.
- 45. Пример. Вычислить определенный интеграл Решение.
- 46. Основные понятия теории дифференциальных уравнений
- 47. Уравнения первого порядка Общий вид дифференциального
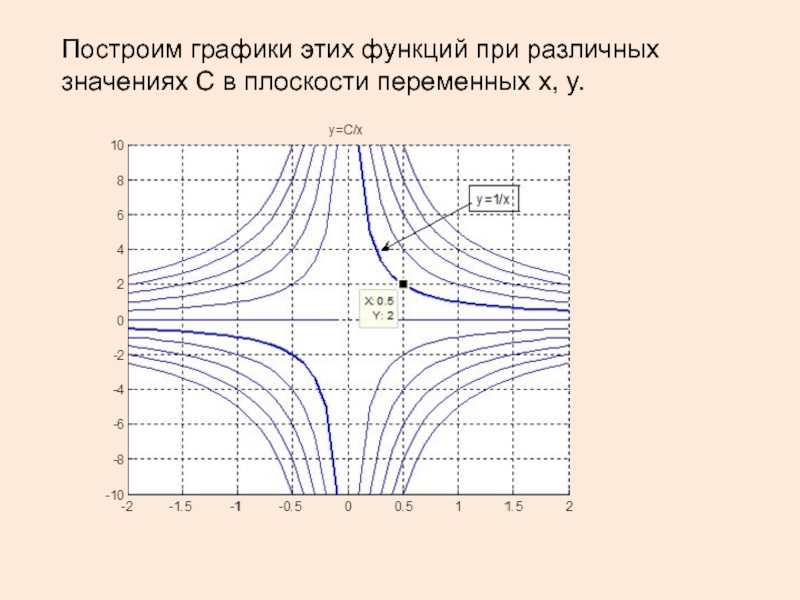
- 48. Построим графики этих функций при различных
- 49. Формула (*) определяет общее решение уравнения, представляющее
- 50. Для произвольного дифференциального уравнения первого порядка общее
- 51. Уравнения с разделяющимися переменными Если в
- 52. Пример. Решить дифференциальное уравнение
- 53.
- 54.
- 55. Линейные однородные дифференциальные уравнения второго
- 56. Если уравнение (*) имеет два различных действительных
- 57. Пример 1. Решить уравнение y``
- 58.
- 59. Пример 3. Решить уравнение
Слайд 1 Б.1.13. Математика 38.03.02 Менеджмент Маркетинг, Менеджмент недвижимости, Производственный менеджмент 38.03.01 Экономика Бухгалтерский учет анализ и
аудит,
Экономика предприятий и организаций
Слайд 2Введение
Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем
самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
Слайд 4
Сумма (разность) двух матриц и одинакового размера определяется следующим
образом:
Для умножения матрицы на число нужно каждый элемент матрицы умножить на это число
Для умножения матрицы на число нужно каждый элемент матрицы умножить на это число
Слайд 5Произведением матрицы A из m строк и k столбцов на
матрицу B из k строк и n столбцов называется матрица
где
где
Слайд 7Правило Крамера и определители матриц
2-го и 3-го порядков
Рассмотрим матрицу второго
порядка:
Число называется определителем
матрицы А и обозначается следующим образом
=
Число называется определителем
матрицы А и обозначается следующим образом
=
Слайд 9 Решение системы трех уравнений с тремя неизвестными
выражается через определители третьего
порядка по фор-мулам Крамера:
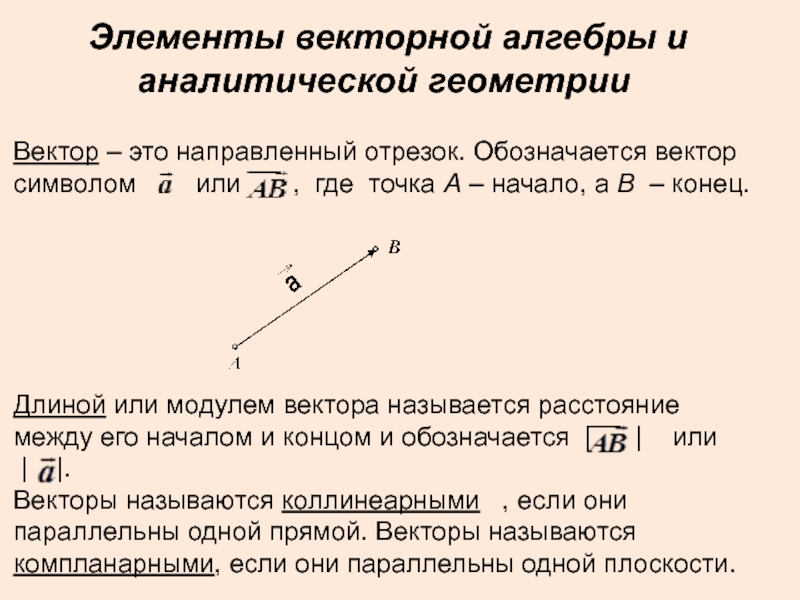
Слайд 10Вектор – это направленный отрезок. Обозначается вектор символом
или , где точка А – начало, а В – конец.
Длиной или модулем вектора называется расстояние между его началом и концом и обозначается | | или
| |.
Векторы называются коллинеарными , если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.
Длиной или модулем вектора называется расстояние между его началом и концом и обозначается | | или
| |.
Векторы называются коллинеарными , если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.
Элементы векторной алгебры и аналитической геометрии
Слайд 11Линейные операции над векторами
Произведением вектора на число к называется
вектор
, который:
имеет длину
коллинеарен вектору
если , то ;
если , то ;
если , то .
, который:
имеет длину
коллинеарен вектору
если , то ;
если , то ;
если , то .
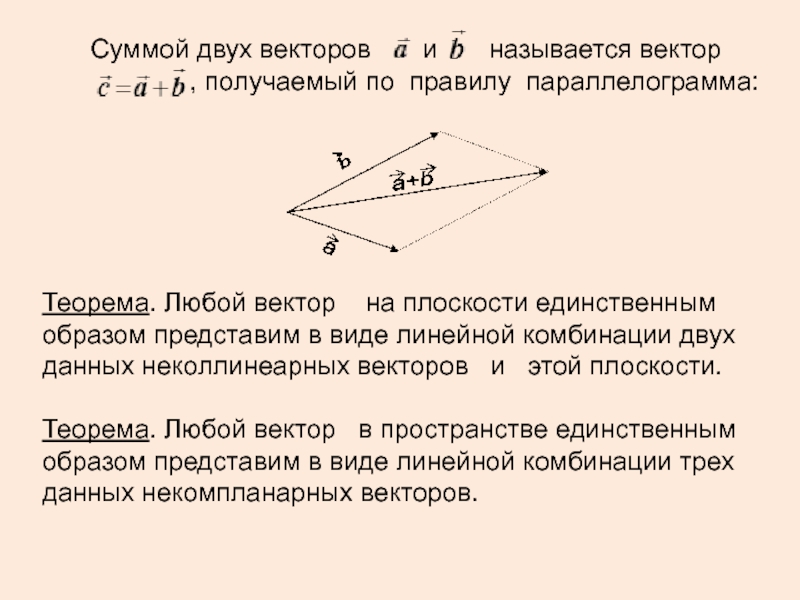
Слайд 12Суммой двух векторов и называется
вектор
, получаемый по правилу параллелограмма:
Теорема. Любой вектор на плоскости единственным образом представим в виде линейной комбинации двух данных неколлинеарных векторов и этой плоскости.
Теорема. Любой вектор в пространстве единственным образом представим в виде линейной комбинации трех данных некомпланарных векторов.
, получаемый по правилу параллелограмма:
Теорема. Любой вектор на плоскости единственным образом представим в виде линейной комбинации двух данных неколлинеарных векторов и этой плоскости.
Теорема. Любой вектор в пространстве единственным образом представим в виде линейной комбинации трех данных некомпланарных векторов.
Слайд 13Базисом
называются взятые в определенном порядке линейно независимые векторы.
Если базисные векторы взаимно перпендикулярны, то базис называется ортогональным, а если плюс к этому базисные векторы имеют единичную длину, то – ортонормированным.
Выражение данного вектора в виде линейной комбинации базисных векторов называется его разложением в данном базисе (или по базису)
Коэффициенты разложения называются координатами вектора в данном базисе.
Если базисные векторы взаимно перпендикулярны, то базис называется ортогональным, а если плюс к этому базисные векторы имеют единичную длину, то – ортонормированным.
Выражение данного вектора в виде линейной комбинации базисных векторов называется его разложением в данном базисе (или по базису)
Коэффициенты разложения называются координатами вектора в данном базисе.
Слайд 14
Декартовой прямоугольной системой координат называется совокупность фиксированной точки О (начала координат)
и базиса векторов , исходящих из
точки О.
Оси, проходящие через базисные векторы, называют соответственно
осью абсцисс (ось ОХ ),
осью ординат (ось ОУ),
осью аппликат (ось OZ).
точки О.
Оси, проходящие через базисные векторы, называют соответственно
осью абсцисс (ось ОХ ),
осью ординат (ось ОУ),
осью аппликат (ось OZ).
Слайд 15Радиус-вектором произвольной точки М называют вектор
, а его координаты называют координатами этой точки.
Для произвольной точки М в декартовой системе координат с ортонормированным базисом в разложении вектора
его координаты являются проекциями вектора на оси.
Длина вектора может быть найдена по формуле
Для произвольной точки М в декартовой системе координат с ортонормированным базисом в разложении вектора
его координаты являются проекциями вектора на оси.
Длина вектора может быть найдена по формуле
Слайд 16Скалярное произведение
Скалярным произведением векторов
называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны (ортогональны)
Скалярное произведение в прямоугольных координатах:
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны (ортогональны)
Скалярное произведение в прямоугольных координатах:
Слайд 17С помощью скалярного произведения можно вычислить угол между векторами:
В частности,
условие ортогональности двух векторов выражается через их координаты следующим образом
Слайд 18Прямая линия на плоскости
Общее уравнение прямой – уравнение прямой L,
проходящей
через заданную точку
перпендикулярно заданному вектору :
или
перпендикулярно заданному вектору :
или
Слайд 19Уравнение прямой с угловым коэффициентом
прямая L пересекает ось ординат в точке
(0, b) и образует с положительным направлением оси абсцисс угол α , тангенс которого равен к .
Слайд 20Уравнение прямой, проходящей через две заданные точки
Положительный угол φ, который отсчитывается
от
прямой до прямой находится по
формуле
прямой до прямой находится по
формуле
Слайд 21
Пример 1. Составить общее уравнение прямой на плоскости, если она проходит
через точку и вектор нормали к ней .
Решение. Используя формулу общего уравнения прямой, получаем:
Решение. Используя формулу общего уравнения прямой, получаем:
Слайд 22Пример 2. Найти угол между прямыми, заданными общими уравнениями
и .
Решение. Используя формулу, получаем:
Получаем угол .
Решение. Используя формулу, получаем:
Получаем угол .
Слайд 23Пример 3. Написать уравнение прямой, которая проходит через две заданные точки
(-1, 2) и (2, 1).
Решение.
По уравнению
полагая в нем x1 = -1, y1 = 2, x2 = 2, y2 = 1 (без разницы, какую точку считать первой, какую - второй), получим
= или =
после упрощений получаем окончательно искомое
уравнение в виде x + 3y - 5 = 0.
Решение.
По уравнению
полагая в нем x1 = -1, y1 = 2, x2 = 2, y2 = 1 (без разницы, какую точку считать первой, какую - второй), получим
= или =
после упрощений получаем окончательно искомое
уравнение в виде x + 3y - 5 = 0.
Слайд 24Элементы математического анализа
Пусть заданы два множества X и Y произвольной природы.
Допустим, что каждому элементу x некоторого подмножества поставлен в соответствие определенный элемент . Это соответствие (отображение) называют функцией y от x и обозначают
.
Множество D называется областью определения функции, а множество всех элементов y, которые соответствуют элементам множества D, называется областью значений этой функции.
.
Множество D называется областью определения функции, а множество всех элементов y, которые соответствуют элементам множества D, называется областью значений этой функции.
Слайд 25Предел функции — одно из основных понятий математического анализа. Функция f(x)
имеет предел A в точке x_0 если для всех значений x, достаточно близких к x_0, значение f(x) близко к A.
Первый замечательный предел:
Второй замечательный предел:
Первый замечательный предел:
Второй замечательный предел:
Слайд 27Дифференцирование
Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость
изменения функции (в данной точке).
Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрированием.
Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрированием.
Слайд 28Вычисление производных
Правила дифференцирования:
Производная суммы конечного числа дифференцируемых функций равна сумме производных
этих функций
Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой функции
Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой функции
Слайд 29
Постоянный множитель при дифференцировании выносится за знак производной
Производная частного вычисляется по
следующей формуле
Слайд 31Производная сложной функции по независимой переменной равна произведению производной функции по
промежуточной переменной на производную промежуточной переменной по независимой переменной:
Пример
Найти производную функции
Решение.
=
Пример
Найти производную функции
Решение.
=
Слайд 33Пример. Найти экстремумы функции
Функция определена на всей числовой прямой. Её производная
всюду существует, поэтому абсциссы точек подозрительных на экстремум это те значения переменной, при которых производная равна нулю, т. е. х = -1 и х = 1. Отметим на следующей схеме знаки производной в соответствующих интервалах
Отсюда видно, что в интервале функция возрастает, а в интервале – убывает, значит, при
функция имеет максимум . Соответственно, .
Слайд 34Интегрирование
Функция F(x) называется первообразной для функции f(x) на интервале X=(a, b)
(конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е.
Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом
Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом
Слайд 38Интегрирование методами подстановки и замены переменной.
Формула подстановки
Пример. Вычислить
Решение. Делая
в этой формуле подстановку , получим
откуда найдем
откуда найдем
Слайд 40Формула интегрирования по частям
Пример. Вычислить
Решение. Введем обозначения:
,
Тогда ,
Применяя формулу интегрирования по частям, получим:
Тогда ,
Применяя формулу интегрирования по частям, получим:
Слайд 41Определённым интегралом функции на промежутке называется конечный предел интегральных
сумм
если он существует и не зависит ни от способа разбиения промежутка , ни от выбора точек .
Ценность этого математического понятия состоит в том, что функцию можно «наполнять» разным содержанием: это может быть функция, определяющая границу криволинейной трапеции, и тогда определенный интеграл выражает площадь трапеции, или это может быть функция, определяющая линейную плотность неоднородного стержня, и тогда определенный интеграл выражает массу стержня.
если он существует и не зависит ни от способа разбиения промежутка , ни от выбора точек .
Ценность этого математического понятия состоит в том, что функцию можно «наполнять» разным содержанием: это может быть функция, определяющая границу криволинейной трапеции, и тогда определенный интеграл выражает площадь трапеции, или это может быть функция, определяющая линейную плотность неоднородного стержня, и тогда определенный интеграл выражает массу стержня.
Слайд 42Формула Ньютона – Лейбница вычисления определенного интеграла:
Формула интегрирования по частям:
Слайд 43Пример. Найти площадь фигуры, ограниченной линией
осью абсцисс и прямой . Искомая
площадь (см. рис.) выражается интегралом
Интегрируем по частям
Слайд 44Правило замены переменной в определённом интеграле.
Пусть требуется вычислить интеграл
.
Заменим , причем концам промежутка соответствуют концы промежутка ,
или .
При этих условиях имеют место формула:
.
Заменим , причем концам промежутка соответствуют концы промежутка ,
или .
При этих условиях имеют место формула:
.
Слайд 45Пример. Вычислить определенный интеграл
Решение. Произведём замену переменной, полагая
Тогда dt = 2x dx, откуда x dx = (1/2) dt, и
подынтегральное выражение преобразуется так:
Найдём новые пределы интегрирования. Подстановка
значений x = 4 и x = 5 в уравнение дает
Используя теперь формулу, получим
подынтегральное выражение преобразуется так:
Найдём новые пределы интегрирования. Подстановка
значений x = 4 и x = 5 в уравнение дает
Используя теперь формулу, получим
Слайд 46
Основные понятия теории дифференциальных
уравнений
Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную
функцию и ее производные.
Решением уравнения назовем любую функцию, обращающую это уравнение в тождество. Порядком дифференциального уравнения называют порядок наивысшей производной, входящей в это уравнение.
Решением уравнения назовем любую функцию, обращающую это уравнение в тождество. Порядком дифференциального уравнения называют порядок наивысшей производной, входящей в это уравнение.
Слайд 47Уравнения первого порядка
Общий вид дифференциального уравнения первого порядка:
Пример. Пусть имеется уравнение
Непосредственной подстановкой убеждаемся в том, что функции
(*)
обращают это уравнение в тождество.
Слайд 49Формула (*) определяет общее решение уравнения, представляющее собой семейство кривых.
Выберем
точку с координатами (на рис. это точка (0.5, 2)). Через нее проходит кривая из семейства (*), которой соответствует значение . Соответствующее решение
называют частным решением дифференциального уравнения, удовлетворяющим начальным условиям
называют частным решением дифференциального уравнения, удовлетворяющим начальным условиям
Слайд 50Для произвольного дифференциального уравнения первого порядка общее решение имеет вид функции
содержащей
параметр С. Графики функций этого семейства называют интегральными кривыми.
Задачей Коши называют нахождение частного решения, удовлетворяющего данным начальным условиям .
Задачей Коши называют нахождение частного решения, удовлетворяющего данным начальным условиям .
Слайд 51Уравнения с разделяющимися переменными
Если в дифференциальном уравнении
правая часть может быть
представлена в виде произведения функций
то такое уравнение называют уравнением с
разделяющимися переменными.
то такое уравнение называют уравнением с
разделяющимися переменными.
Слайд 52Пример. Решить дифференциальное уравнение
Решение. Так как
, то .
Далее разделяем переменные:
Следующий этап – интегрирование дифференциального уравнения:
Ответ. Общее решение y = Cx, где С – константа.
Далее разделяем переменные:
Следующий этап – интегрирование дифференциального уравнения:
Ответ. Общее решение y = Cx, где С – константа.
Слайд 55Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Общий вид:
(**)
Характеристическое уравнение:
(**)
Слайд 56Если уравнение (*) имеет два различных действительных корня
и , то общее решение уравнения (**) имеет вид
Если характеристическое уравнение (*) имеет два одинаковых действительных корня , то общее решение уравнения (**) имеет вид
Если уравнение (*) имеет комплексные корни
то общее решение уравнения (**) имеет вид
Если характеристическое уравнение (*) имеет два одинаковых действительных корня , то общее решение уравнения (**) имеет вид
Если уравнение (*) имеет комплексные корни
то общее решение уравнения (**) имеет вид
Слайд 57
Пример 1. Решить уравнение y`` + 3y` + 2y =
0.
Решение. Данное уравнение является линейным однородным уравнением 2-го порядка с постоянными коэффициентами. Выпишем и решим характеристическое уравнение:
Так как оба корня вещественные и различные, общее решение имеет вид:
Решение. Данное уравнение является линейным однородным уравнением 2-го порядка с постоянными коэффициентами. Выпишем и решим характеристическое уравнение:
Так как оба корня вещественные и различные, общее решение имеет вид:
Слайд 59
Пример 3. Решить уравнение
Решение.
Составим и решим характеристическое уравнение:
Получены
сопряженные комплексные корни.
Ответ: Общее решение:
Ответ: Общее решение: