2018 г.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) презентация
Содержание
- 1. Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
- 2. Физический смысл производной
- 3. Материальная точка движется прямолинейно по закону
- 4. Материальная точка движется прямолинейно по закону
- 5. Материальная точка движется прямолинейно по закону
- 6. Материальная точка движется прямолинейно по закону
- 7. Задача №5 На рисунке показан график движения
- 8. Задача №6 Материальная точка М
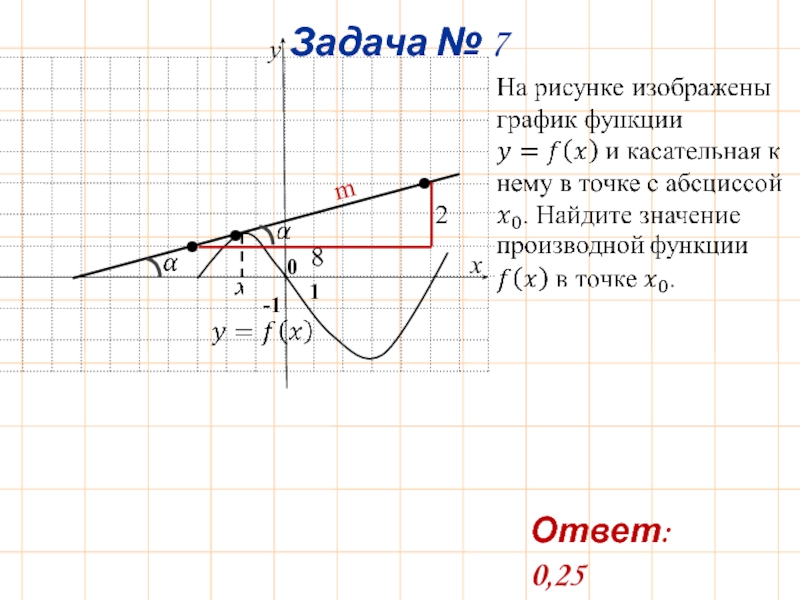
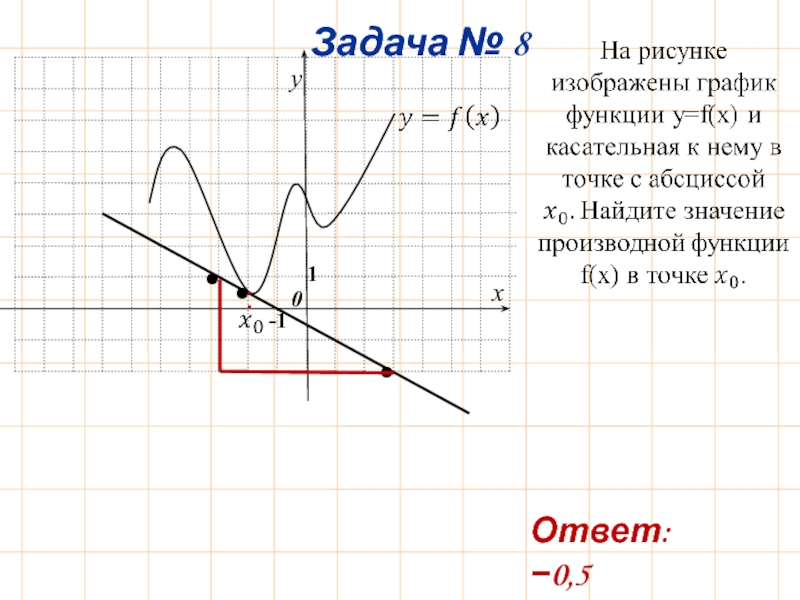
- 9. Геометрический смысл производной, касательная
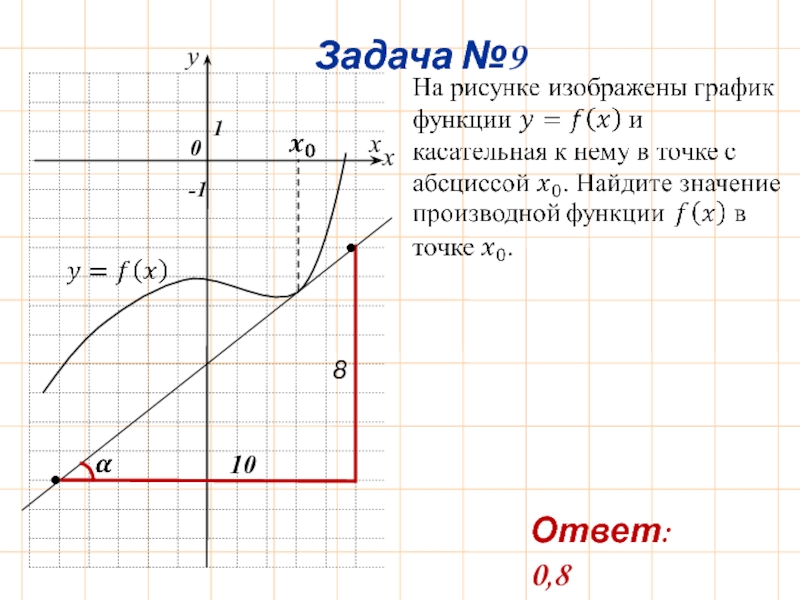
- 10. 2 8 m 0 Ответ: 0,25
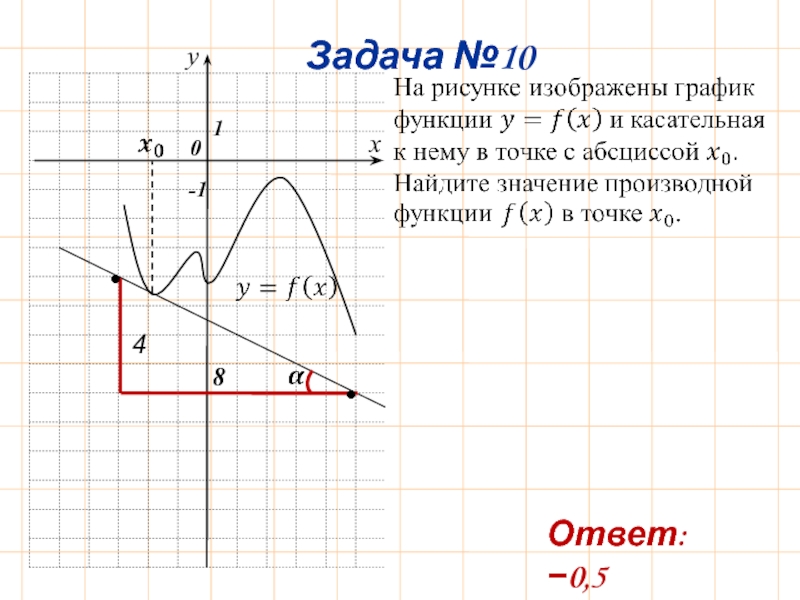
- 11. 0 Ответ: −0,5
- 12. Задача №9 y
- 13. Задача №10 0 x
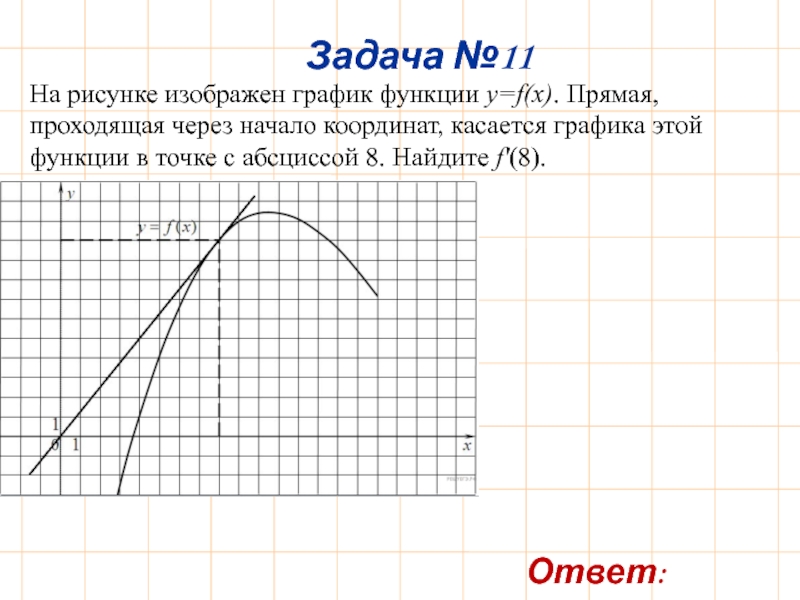
- 14. На рисунке изображен график функции y=f(x). Прямая, проходящая
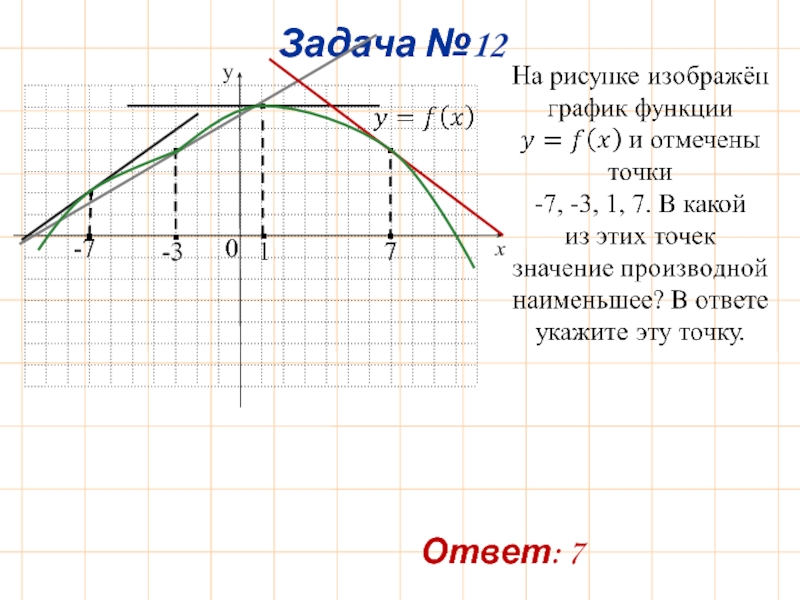
- 15. Задача №12 y x
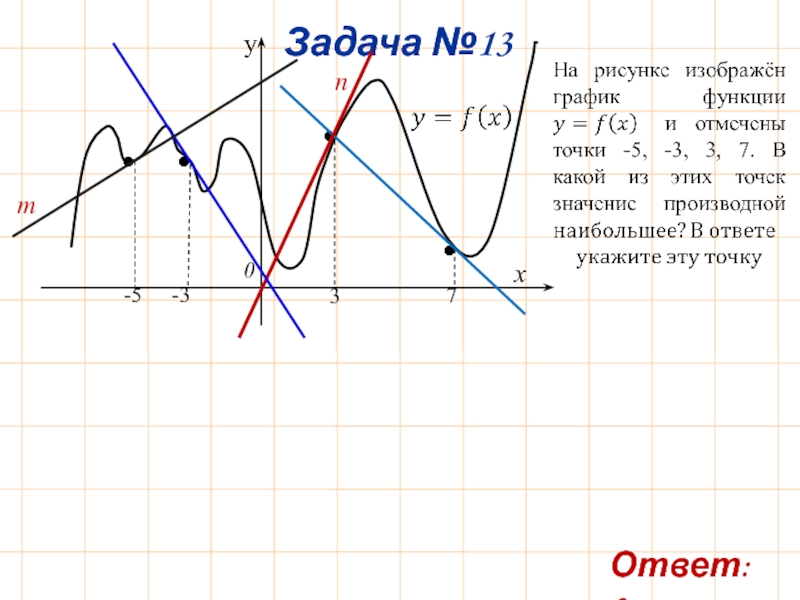
- 16. Задача №13 m n Ответ: 3
- 17. Применение производной к исследованию функций
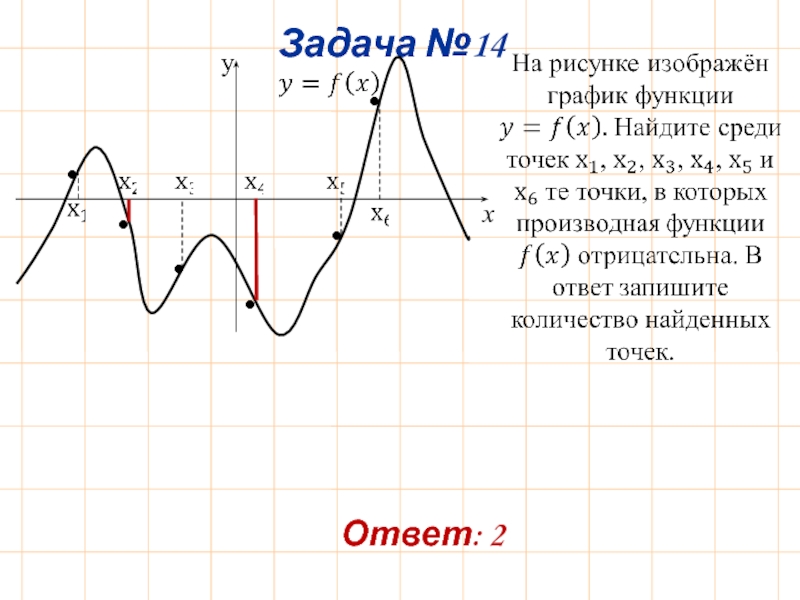
- 18. Задача №14 Ответ: 2
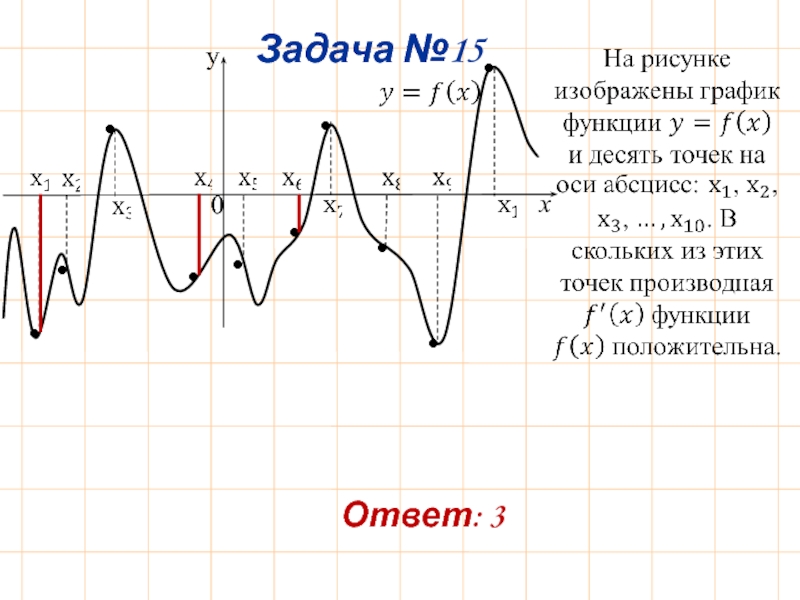
- 19. Задача №15 Ответ: 3
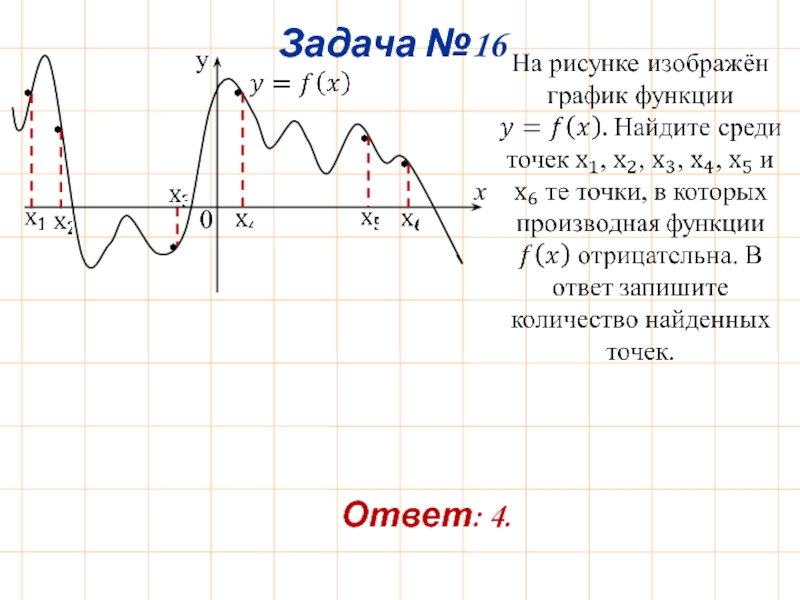
- 20. Задача №16 Ответ: 4.
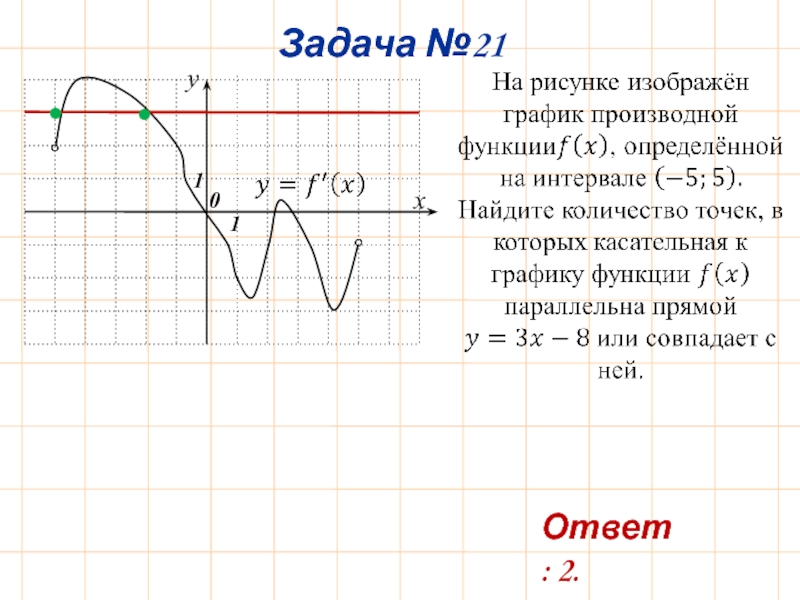
- 21. Задача №17
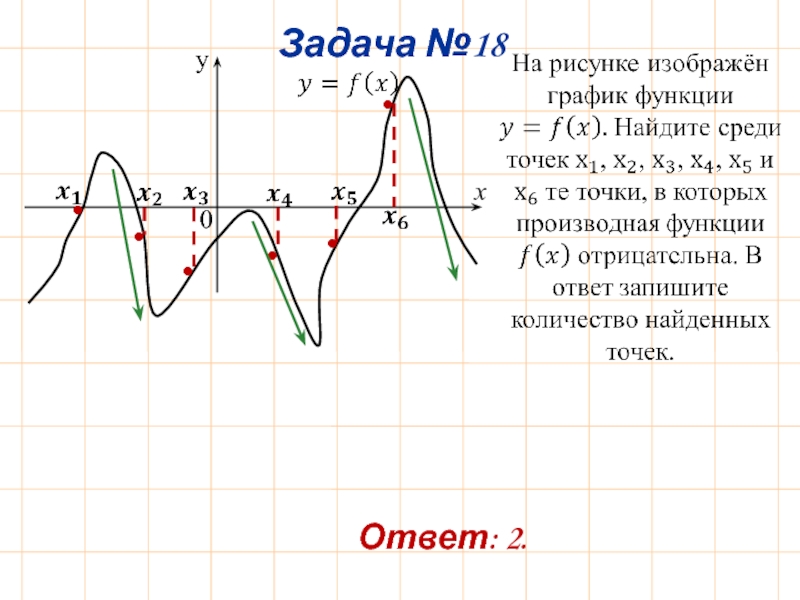
- 22. Задача №18 y Ответ: 2.
- 23. y x Задача №19 0
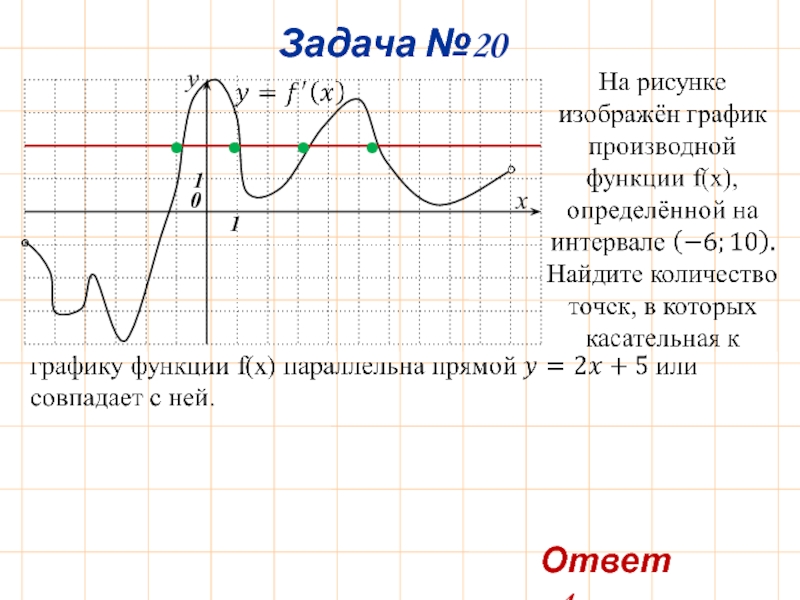
- 24. Задача №20 y x 0 1
- 25. Задача №21 y x 0 1
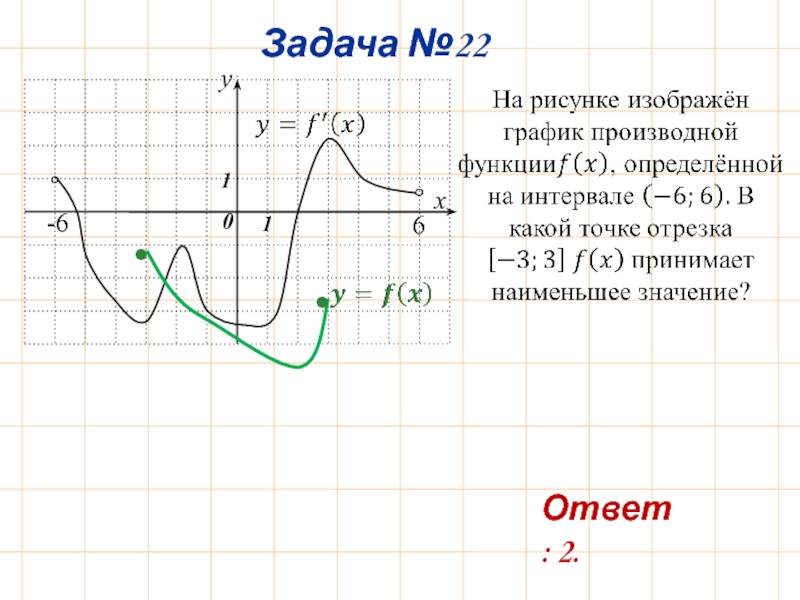
- 26. Задача №22 y
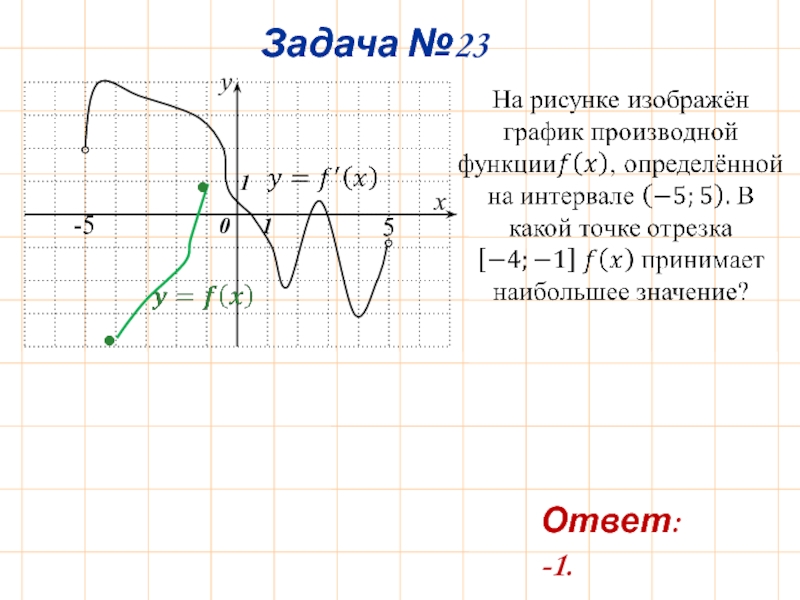
- 27. Задача №23 Ответ: -1. • •
- 28. Задача №24 Задача №25 Ответ:
- 29. Задача №26 Ответ: 2. Прямая y =
- 30. Прямая y = 3x + 4 является касательной к
- 31. Прямая y = 3x + 1 является касательной к графику
- 32. Прямая y = 3x + 4 является касательной к
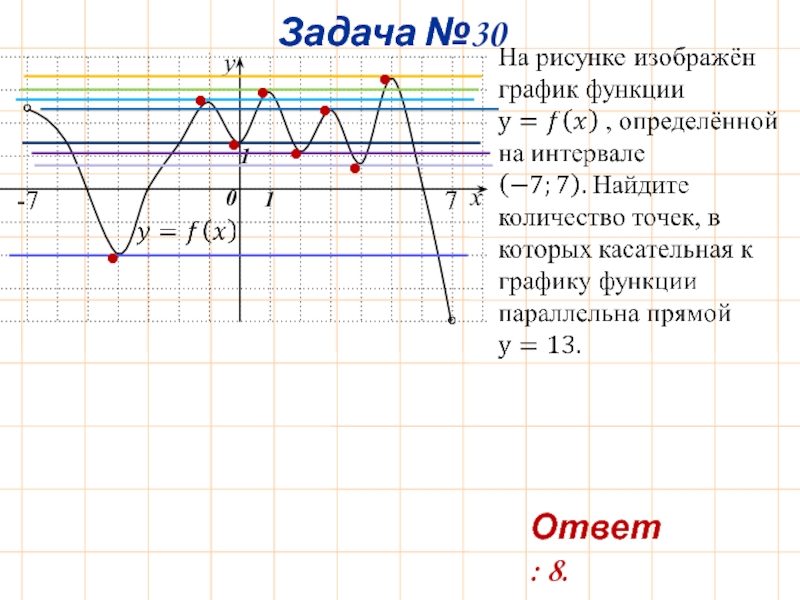
- 33. Задача №30 x • •
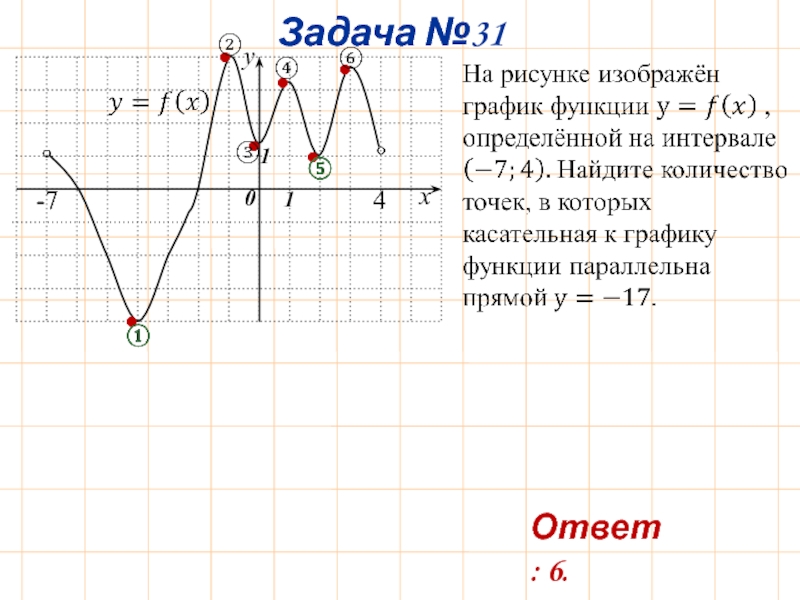
- 34. Задача №31 x
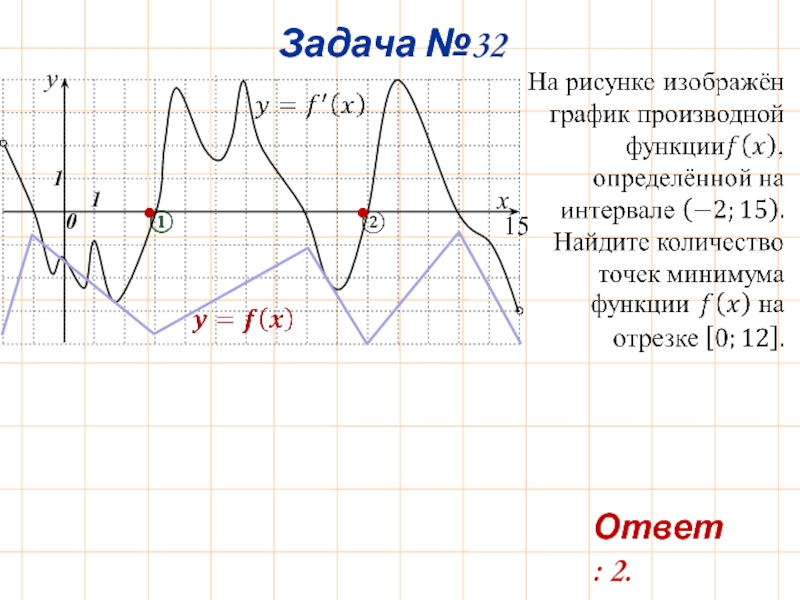
- 35. ② Задача №32 15
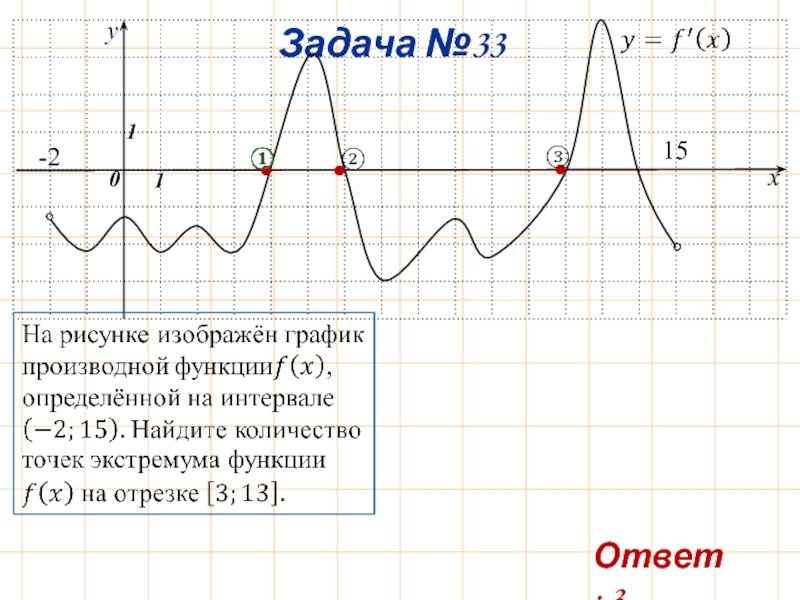
- 36. Задача №33 y x 0 1
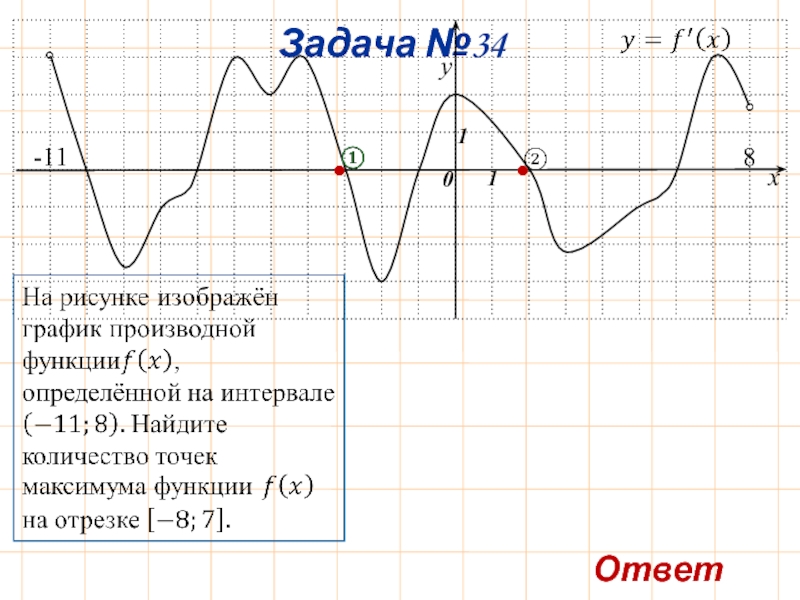
- 37. Задача №34 y x 0 1
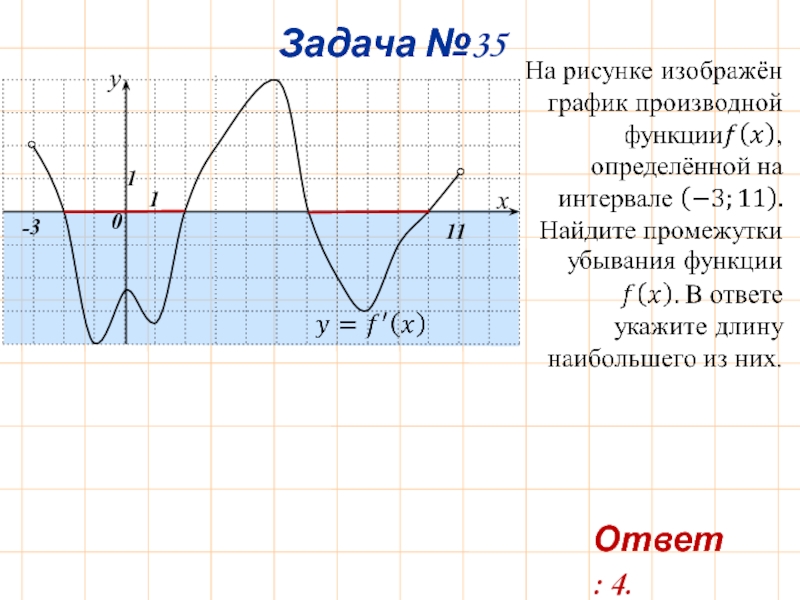
- 38. Задача №35 -3 11 Ответ: 4.
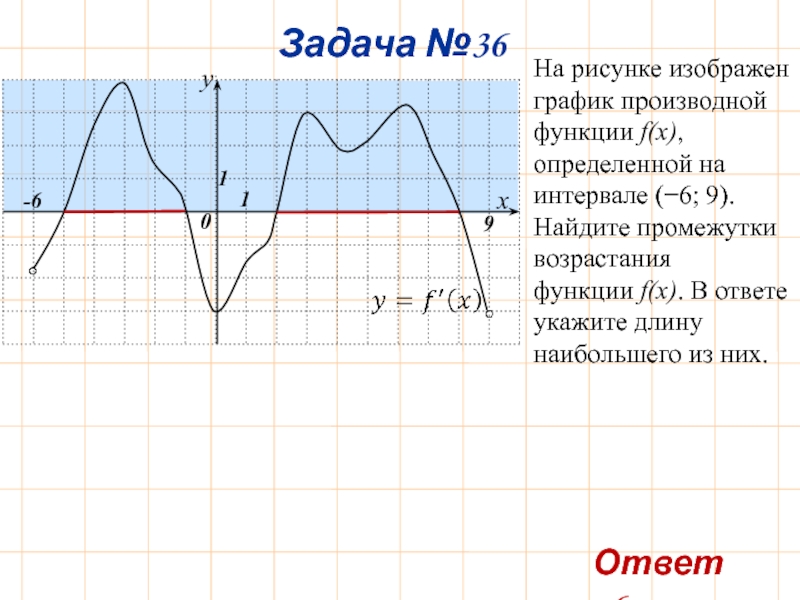
- 39. Задача №36 -6 9
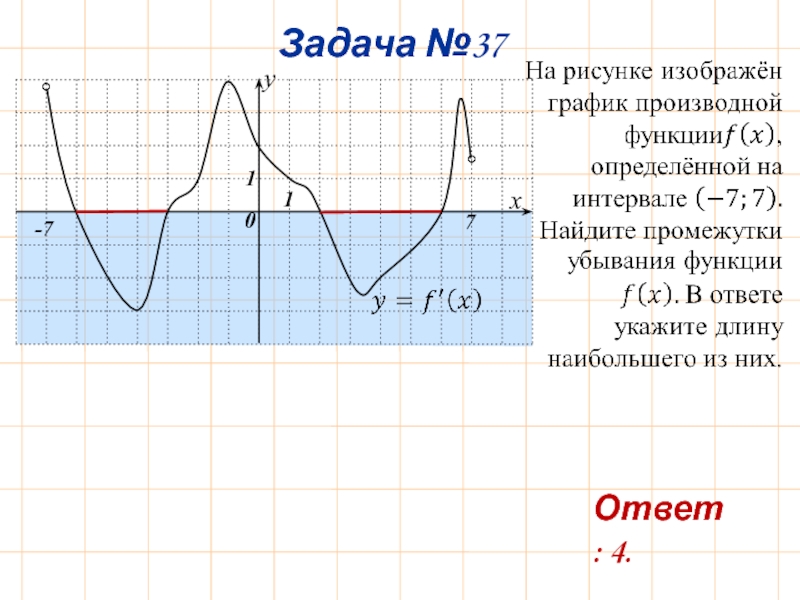
- 40. Задача №37 7 -7 Ответ: 4.
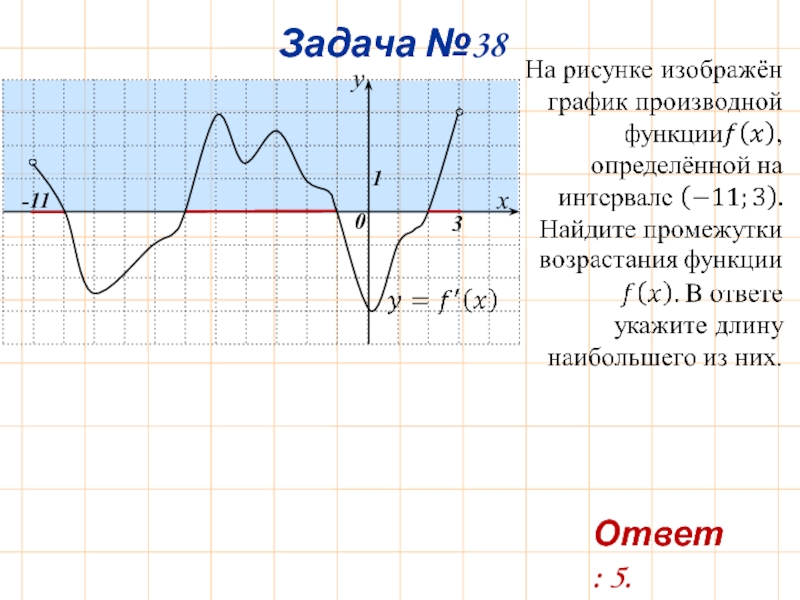
- 41. Задача №38 -11 3 Ответ: 5.
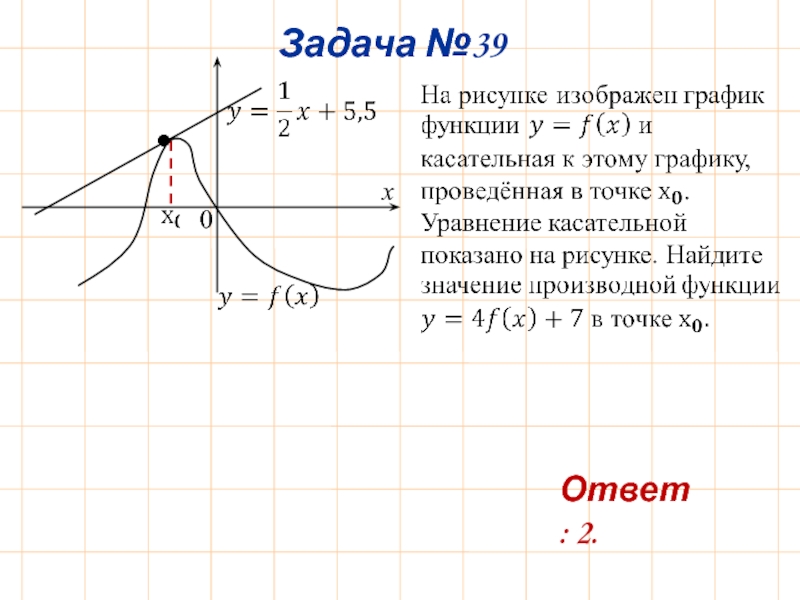
- 42. Задача №39 0 x • Ответ: 2.
- 43. y 0
- 44. Первообразная Интеграл
- 45. Задача №42 На рисунке изображён график некото-рой
Слайд 1Методическое пособие для учащихся 11 классов
Производная. Первообразная. Интеграл .
(по материалам открытого
Слайд 3Материальная точка движется прямолинейно по закону
(где x — расстояние от точки
Задача №1
Ответ: 60 м/с.
Слайд 4Материальная точка движется прямолинейно по закону
(где x — расстояние от точки
Задача №2
Ответ: 20 м/с.
Слайд 5Материальная точка движется прямолинейно по закону
(где x — расстояние от точки
Задача №3
Ответ: 59 м/с.
Слайд 6Материальная точка движется прямолинейно по закону
(где x — расстояние от точки
Задача №4
Ответ: 7с.
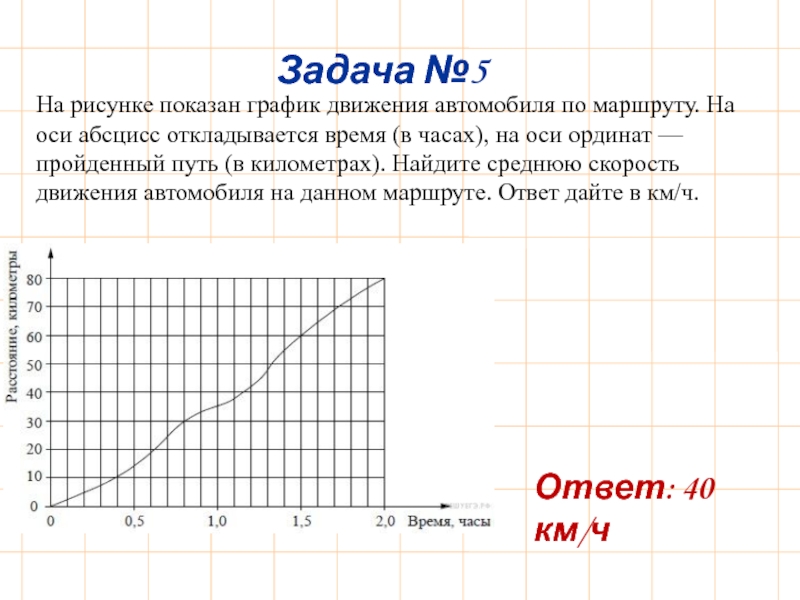
Слайд 7Задача №5
На рисунке показан график движения автомобиля по маршруту. На оси
Ответ: 40 км/ч
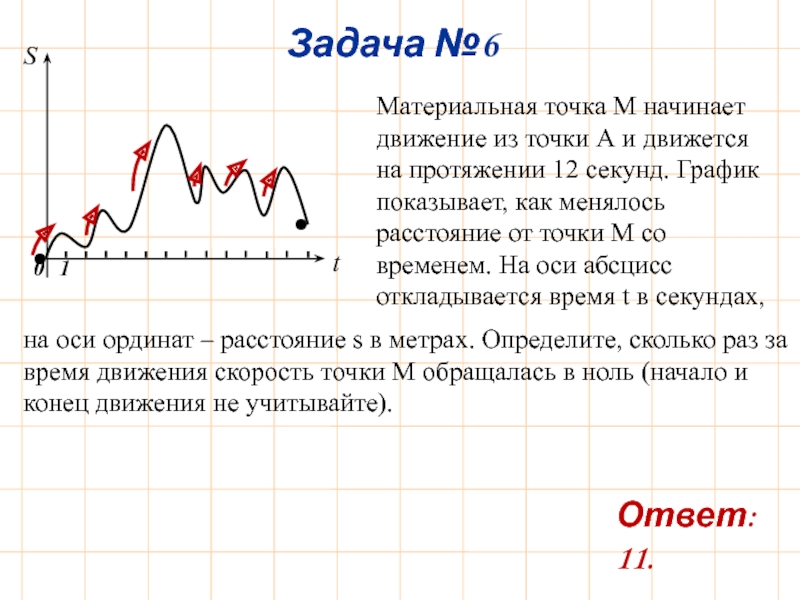
Слайд 8Задача №6
Материальная точка М начинает движение из точки А и движется
на оси ординат – расстояние s в метрах. Определите, сколько раз за время движения скорость точки М обращалась в ноль (начало и конец движения не учитывайте).
Ответ: 11.
Слайд 14На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается
Задача №11
Ответ: 1,25
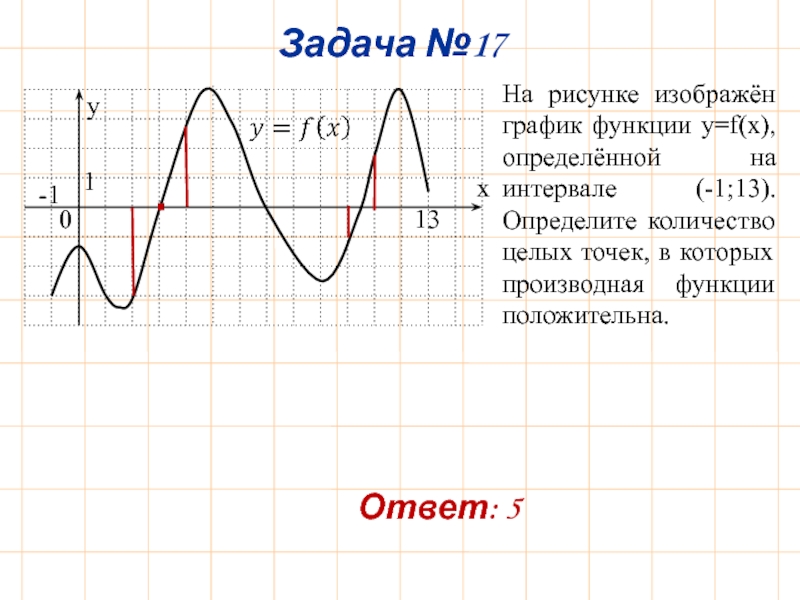
Слайд 21Задача №17
y
x
0
1
-1
13
На рисунке изображён график функции y=f(x), определённой на интервале
Ответ: 5
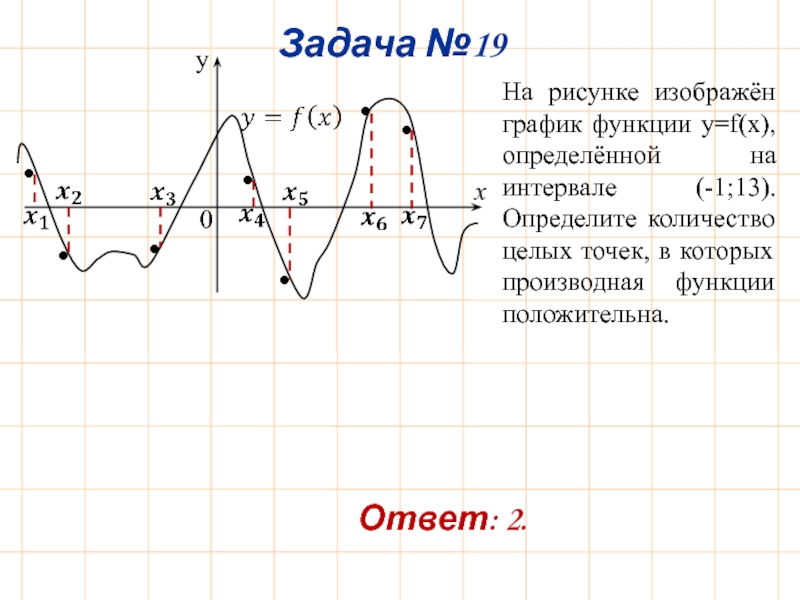
Слайд 23y
x
Задача №19
0
•
•
•
•
•
•
•
На рисунке изображён график функции y=f(x), определённой на интервале (-1;13).
Ответ: 2.
Слайд 28Задача №24
Задача №25
Ответ: 1.
Ответ: -0,5.
Прямая y = 6x + 9 параллельна касательной к
y = x2 + 7x − 6. Найдите абсциссу точки касания.
Прямая y = − 4x − 8 является касательной к графику функции
y = x3 − 3x2 − x − 9. Найдите абсциссу точки касания.
Слайд 29Задача №26
Ответ: 2.
Прямая y = 5x + 14 является касательной к графику функции
y = x3 − 4x2 + 9 x +14. Найдите абсциссу точки касания.
Слайд 30Прямая y = 3x + 4 является касательной к графику функции
y =
Задача №27
Решение.
Значение производной функции в точке касания
равно угловому коэффициенту касательной, т. е. y / = 3
y / = 3 x2 + 8x + 3
3 x2 + 8x + 3 = 3
x(3x+8) = 0. Отсюда x = 0 или x = 8/3
Уравнению x3 + 4x2 + 3x + 4 = 3x + 4 удовлетворяет только
x = 0. Значит, абсцисса точки касания равна 0, а тогда ее
ордината равна 4.
Ответ: 4.
Слайд 31Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
По
функции − парабола. Касательная к параболе
(а также и к гиперболе) имеет с ней единственную
общую точку. Поэтому необходимо и достаточно, чтобы уравнение ax2 + 2x + 3 = 3x + 1 имело единственно решение.
Получим ax2 + 2x + 3 − 3x − 1
ax2 − x + 2 = 0
D = 1 − 8а
Для этого дискриминант должен быть равен нулю, откуда
1 − 8а = 0
a = 1/8 = 0,125
Задача №28
Решение.
Ответ: 0,125.
Слайд 32Прямая y = 3x + 4 является касательной к графику функции
3x2 −
Задача №29
Решение.
График заданной функции − парабола. Касательная к параболе
имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение 3x2 − 3x + с = 3x + 4 имело единственно решение. Получим
3x2 − 6x + с − 4 = 0
D = 36 − 12(с − 4) = 36 − 12с+ 48 = 84 − 12с
Для этого дискриминант должен быть равен нулю, откуда
84 − 12с = 0
с = 84/12 = 7
Ответ: 7.
Слайд 39
Задача №36
-6
9
Ответ: 6.
На рисунке изображен график производной функции f(x), определенной на интервале
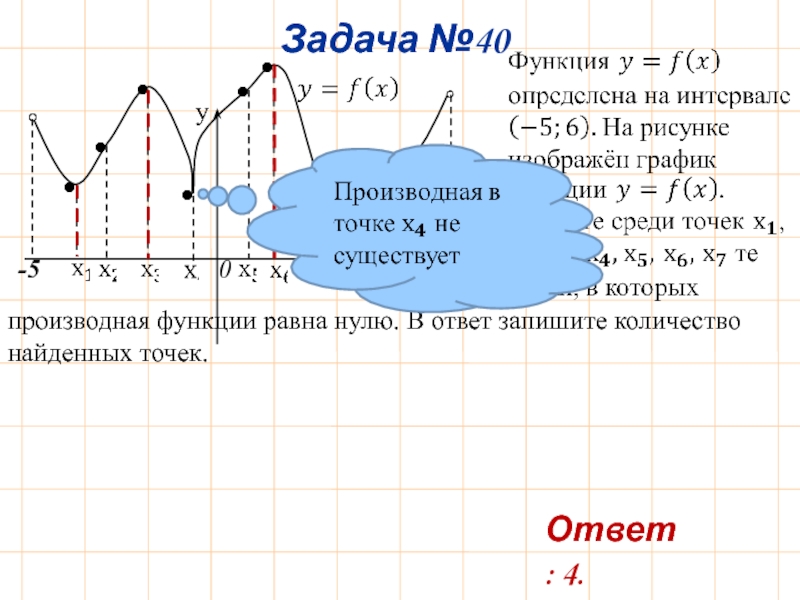
Слайд 43y
0
x
•
•
•
•
•
Задача №40
•
•
-5
6
производная функции равна нулю. В ответ запишите количество найденных точек.
Ответ: 4.
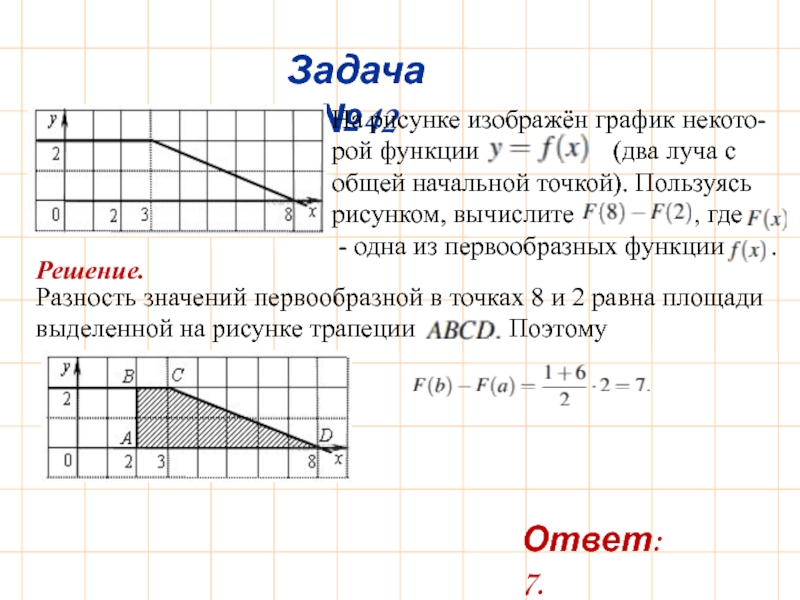
Слайд 45Задача №42
На рисунке изображён график некото-рой функции
- одна из первообразных функции .
Решение.
Ответ: 7.
Разность значений первообразной в точках 8 и 2 равна площади
выделенной на рисунке трапеции Поэтому