- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проект по теме Теорема синусов презентация
Содержание
- 1. Проект по теме Теорема синусов
- 2. Теоре́ма си́нусов — теорема, устанавливающая зависимость между длинами сторон треугольника и величиной противолежащих им углов. Существуют два варианта теоремы;
- 3. Обычная теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
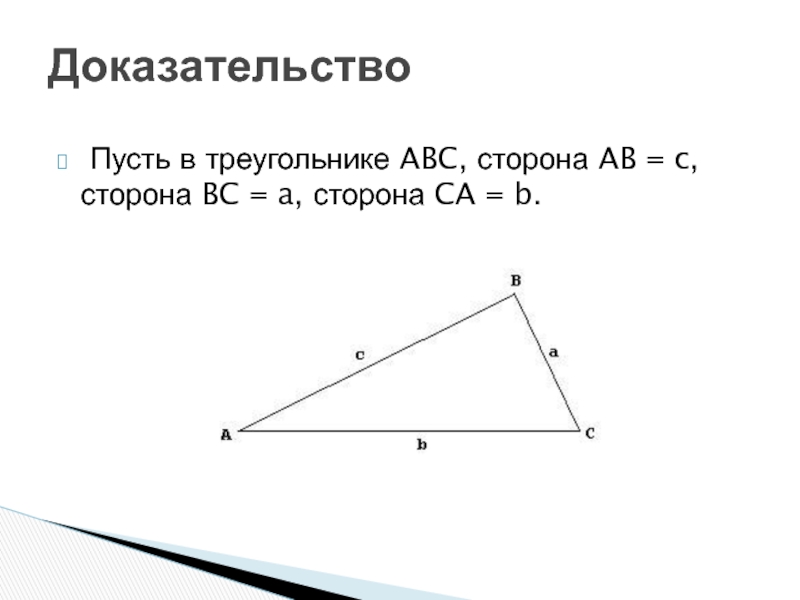
- 4. Пусть в треугольнике ABC, сторона AB =
- 5. Попытаемся доказать, что a/sin(A) = b/sin(B) =
- 6. Для произвольного треугольника a/sin(A) =b/sin(B) = c/sin(C) =
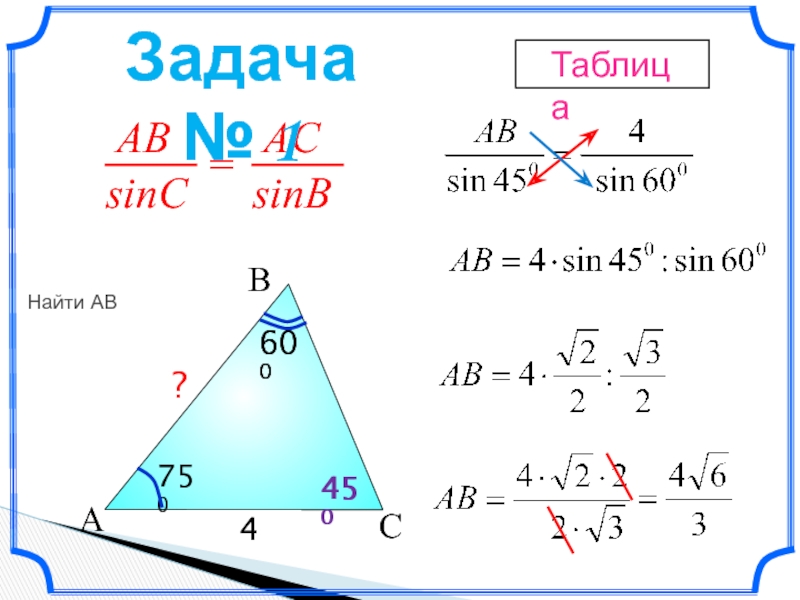
- 7. C A B 750
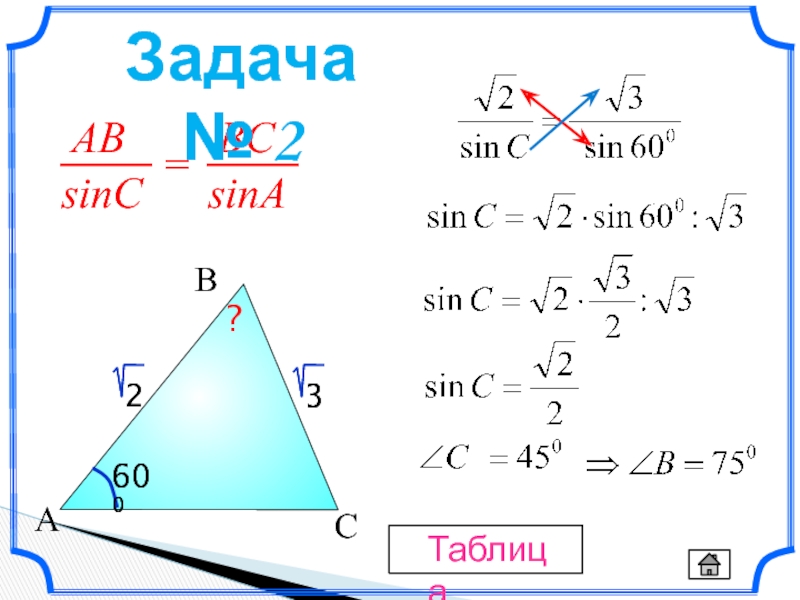
- 8. C A B 600 600
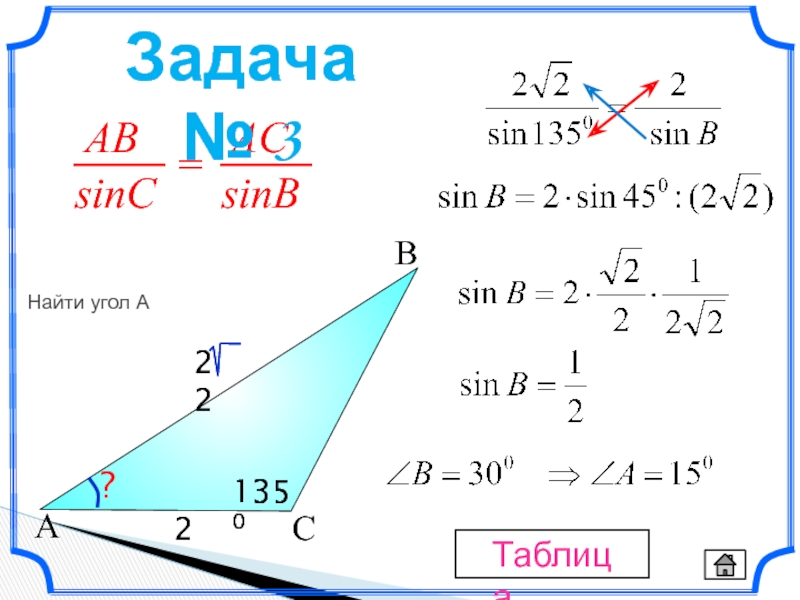
- 9. 2 C A B ?
- 10. Спасибо за внимание!
Теоре́ма си́нусов — теорема, устанавливающая зависимость между длинами сторон треугольника и величиной противолежащих им углов. Существуют два варианта теоремы;
Слайд 2Теоре́ма си́нусов — теорема, устанавливающая зависимость между длинами сторон треугольника и величиной противолежащих им углов. Существуют
два варианта теоремы;
Слайд 5Попытаемся доказать, что a/sin(A) = b/sin(B) = c/sin(C). Воспользуемся теоремой о
площади треугольника, и запишем её для каждой пары сторон и соответствующего им угла:
S = (1/2)*a*b*sin(C),
S = (1/2)*b*c*sin(A),
S = (1/2)*c*a*sin(B).
Так как левые части у первых двух равенств одинаковые, то правые части можно приравнять между собой. Получим (1/2)*a*b*sin(C) = (1/2)*b*c*sin(A). Сократим это равенство на ½*b, получим:
a*sin(C) = c*sin(A).
По свойству пропорции получаем:
a/sin(A) = c/sin(C).
Так как левые части у второго и третьего равенств одинаковые, то правые части можно приравнять между собой. Получим (1/2)*b*c*sin(C) = (1/2)*c*a*sin(B). Сократим это равенство на 1/2*c, получим:
b*sin(A) = a*sin(B).
По свойству пропорции получаем:
a/sin(A) = b/sin(B).
Объединив полученные два результата получаем: a/sin(A) = b/sin(B) = c/sin(C). Что и требовалось доказать.
S = (1/2)*a*b*sin(C),
S = (1/2)*b*c*sin(A),
S = (1/2)*c*a*sin(B).
Так как левые части у первых двух равенств одинаковые, то правые части можно приравнять между собой. Получим (1/2)*a*b*sin(C) = (1/2)*b*c*sin(A). Сократим это равенство на ½*b, получим:
a*sin(C) = c*sin(A).
По свойству пропорции получаем:
a/sin(A) = c/sin(C).
Так как левые части у второго и третьего равенств одинаковые, то правые части можно приравнять между собой. Получим (1/2)*b*c*sin(C) = (1/2)*c*a*sin(B). Сократим это равенство на 1/2*c, получим:
b*sin(A) = a*sin(B).
По свойству пропорции получаем:
a/sin(A) = b/sin(B).
Объединив полученные два результата получаем: a/sin(A) = b/sin(B) = c/sin(C). Что и требовалось доказать.
Слайд 6Для произвольного треугольника
a/sin(A) =b/sin(B) = c/sin(C) = 2*R.
где a,b,c—стороны треугольника, — соответственно противолежащие
им углы, — радиус окружности, описанной около треугольника.
Расширенная теорема синусов:
