прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки равенства прямоугольных треугольников презентация
Содержание
- 1. Признаки равенства прямоугольных треугольников
- 2. Признак равенства прямоугольных треугольников по катету и
- 3. Признак равенства по гипотенузе и острому углу
- 4. Признак равенства прямоугольных треугольников по катету и
- 5. Пример 1. Доказать, что каждая точка биссектрисы
- 6. Пример 2. Доказать, что точка плоскости, равноудаленная
Слайд 2Признак равенства прямоугольных треугольников по катету и гипотенузе
Если катет и
гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Слайд 3Признак равенства по гипотенузе и острому углу
Если гипотенуза и острый
угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Слайд 4Признак равенства прямоугольных треугольников по катету и острому углу
Если катет
и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Слайд 5Пример 1. Доказать, что каждая точка биссектрисы угла равноудалена от его
сторон.
Решение. Пусть l — биссектриса ∠ АОВ (рис.2).
Рассмотрим произвольную точку М, лежащую на луче l. Опустим из точки М перпендикуляры МС и MD на стороны угла АОВ. Прямоугольные треугольники ОМС и OMD равны по теореме 1: у них гипотенуза ОМ общая, а углы СОМ и DOM равны по условию. Отсюда следует, что МС = MD.
Решение. Пусть l — биссектриса ∠ АОВ (рис.2).
Рассмотрим произвольную точку М, лежащую на луче l. Опустим из точки М перпендикуляры МС и MD на стороны угла АОВ. Прямоугольные треугольники ОМС и OMD равны по теореме 1: у них гипотенуза ОМ общая, а углы СОМ и DOM равны по условию. Отсюда следует, что МС = MD.
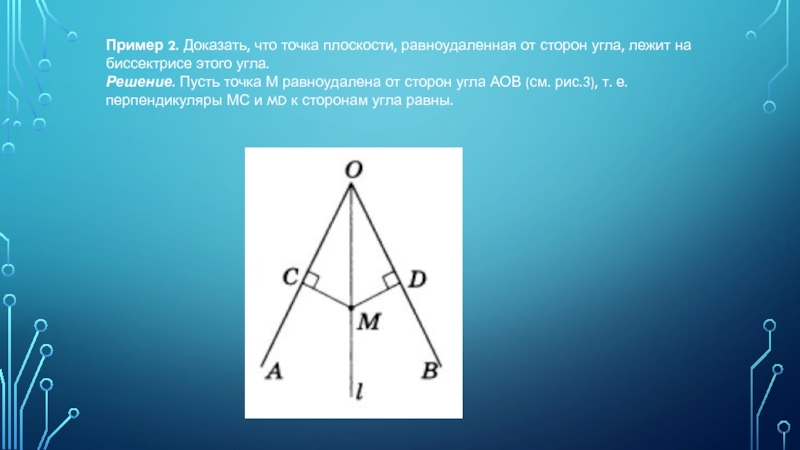
Слайд 6Пример 2. Доказать, что точка плоскости, равноудаленная от сторон угла, лежит
на биссектрисе этого угла.
Решение. Пусть точка М равноудалена от сторон угла АОВ (см. рис.3), т. е. перпендикуляры МС и MD к сторонам угла равны.
Решение. Пусть точка М равноудалена от сторон угла АОВ (см. рис.3), т. е. перпендикуляры МС и MD к сторонам угла равны.