- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признак перпендикулярности плоскостей презентация
Содержание
- 1. Признак перпендикулярности плоскостей
- 2. Определение: Две пересекающиеся плоскости
- 3. Теорема Если плоскость
- 4. Работаем вместе! Рисунок Дано: ___________________ Доказать:
- 5. Проверка работы с формулировкой теоремы Дано:
- 6. Работаем в группах!
- 7. Доказательство: Проведем в плоскости α через точку
- 8. Затребованная помощь I Шаги:
- 9. Затребованная помощь II Обоснование: I. а)
- 10. Затребованная помощь III Описание первого этапа I.
- 11. Затребованная помощь IV Названия этапов: I. Строим
- 12. Проверка Шаги Обоснование I а) a⊥c, a⊂α, Μ∈a
- 13. b c М
- 14. Шаги Обоснование а) γ ⊥ c
- 15. Шаги Обоснование б) a ⊥ b
- 16. Оформление доказательства: I. Строим плоскость γ:
- 17. Спасибо всем за работу!
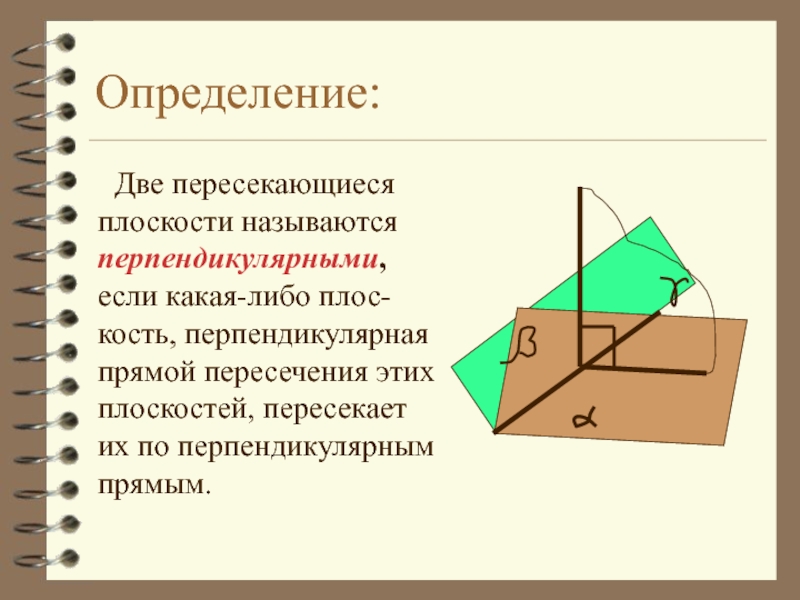
Слайд 2Определение:
Две пересекающиеся плоскости называются перпендикулярными, если какая-либо плос-кость,
Слайд 3Теорема
Если плоскость проходит через прямую, перпендикуляр-ную другой
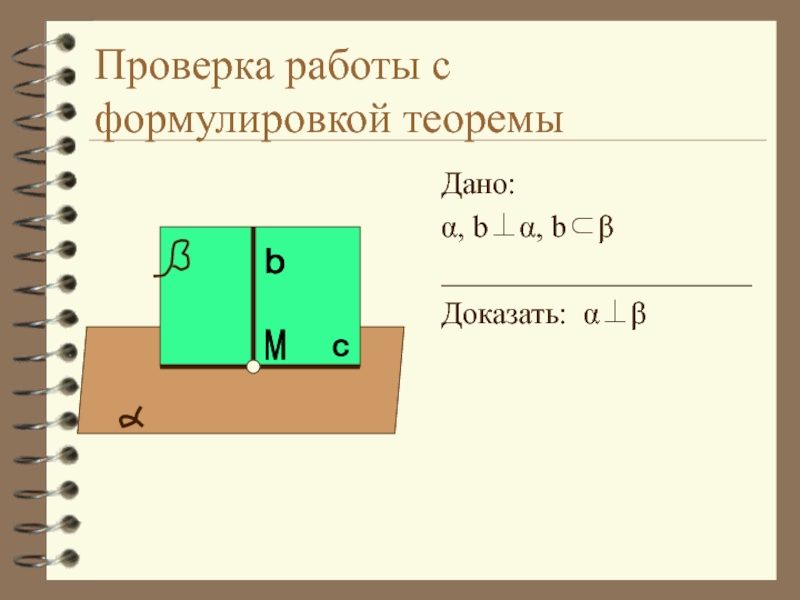
Слайд 5Проверка работы с формулировкой теоремы
Дано:
α, b⊥α, b⊂β
____________________
Доказать: α⊥β
b
c
М
Слайд 7Доказательство:
Проведем в плоскости α через точку пересечения прямой b с плоскостью
Слайд 8Затребованная помощь I
Шаги:
I.
а) a
б) γ (а, b);
II.
а) γ ⊥ c;
б) a ⊥ b.
Значит, α ⊥ β.
Слайд 9Затребованная помощь II
Обоснование:
I.
а) Через каждую точку прямой на плоскости можно
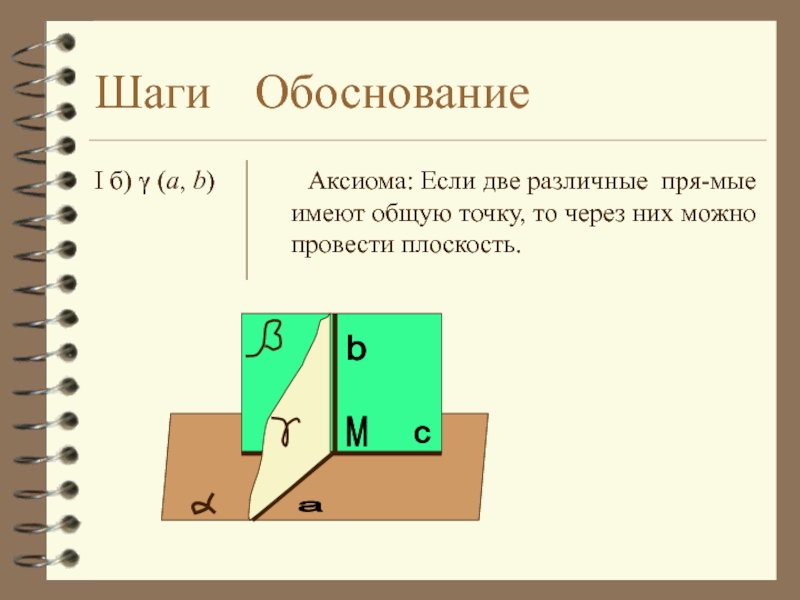
б) Аксиома: Если две различные прямые имеют общую точку, то через них можно провести плоскость.
II.
а) По признаку перпендикулярности прямой и плоскости, так как с⊥а по построению, а b ⊥ с по определению перпендикулярности прямой и плоскости.
б) По определению перпендикулярности прямой и плоскости.
Вывод. По определению перпендикулярных плоскостей.
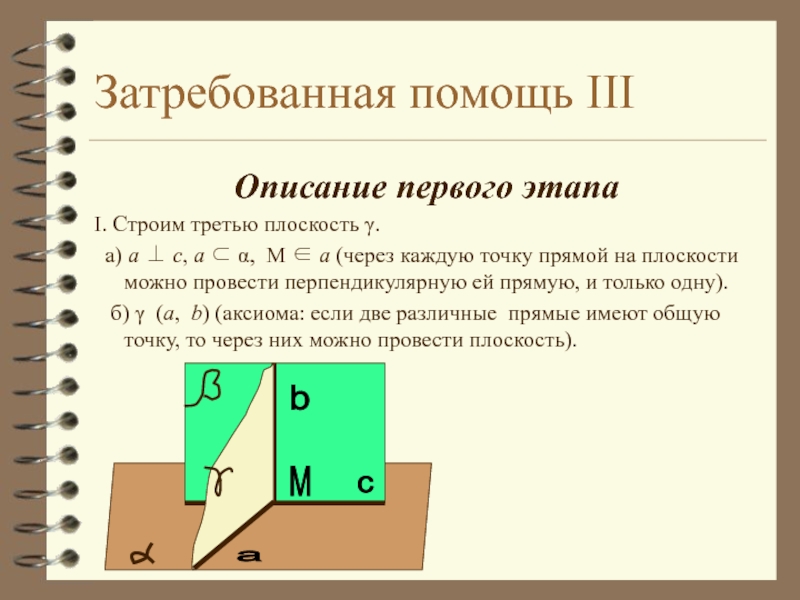
Слайд 10Затребованная помощь III
Описание первого этапа
I. Строим третью плоскость γ.
а) a
б) γ (а, b) (аксиома: если две различные прямые имеют общую точку, то через них можно провести плоскость).
b
c
М
а
Слайд 11Затребованная помощь IV
Названия этапов:
I. Строим третью плоскость γ.
II. Доказываем, что γ
Делаем вывод.
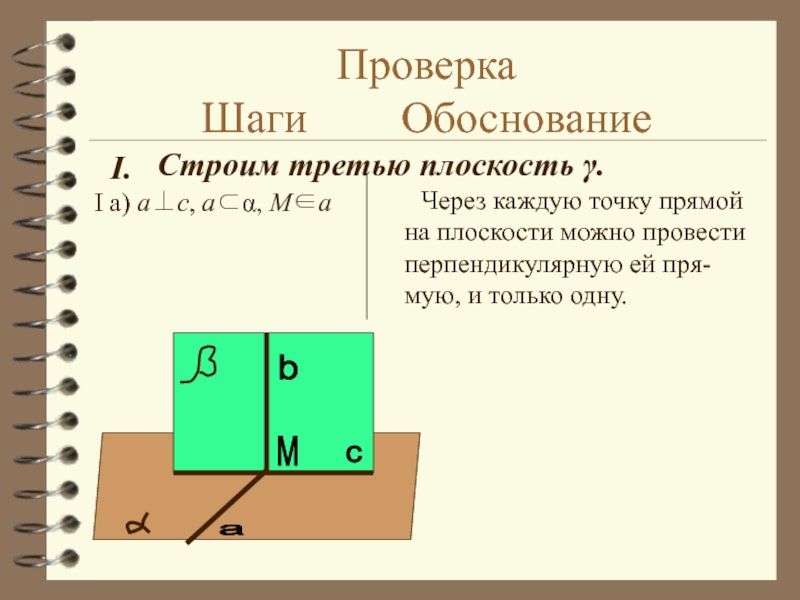
Слайд 12Проверка
Шаги Обоснование
I а) a⊥c, a⊂α, Μ∈a
Через каждую
b
c
М
а
Строим третью плоскость γ.
I.
Слайд 13
b
c
М
а
Шаги Обоснование
I б) γ (а, b)
Слайд 14Шаги Обоснование
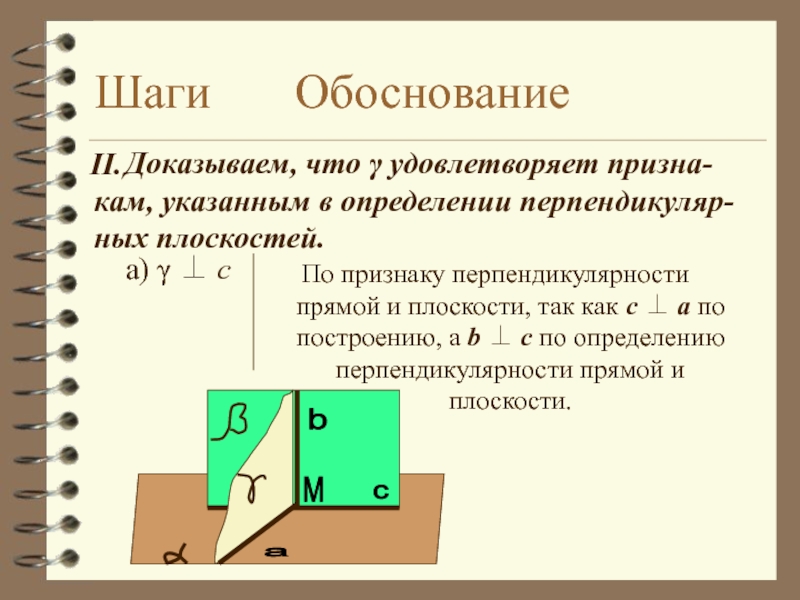
а) γ ⊥ c
По признаку перпендикулярности прямой и плоскости,
Доказываем, что γ удовлетворяет призна-кам, указанным в определении перпендикуляр-ных плоскостей.
b
c
М
а
II.
Слайд 15Шаги Обоснование
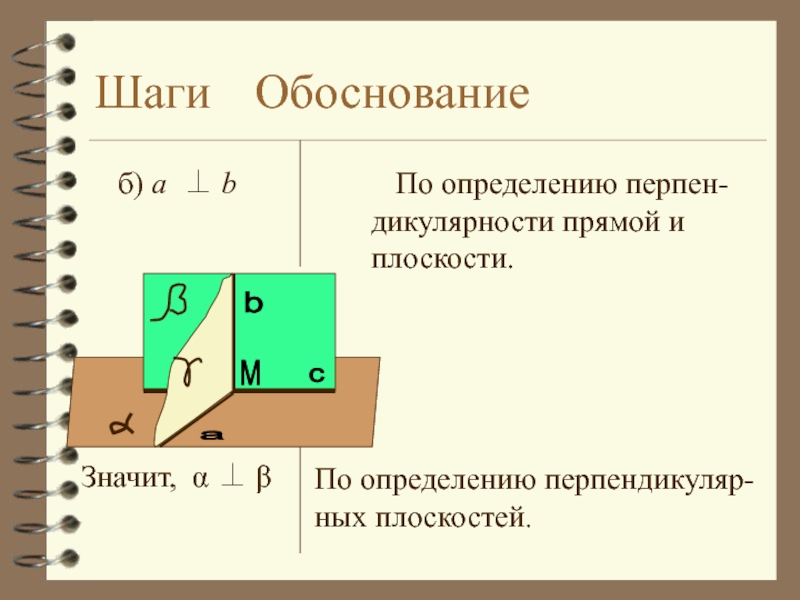
б) a ⊥ b
По определению
Значит, α ⊥ β
По определению перпендикуляр-
ных плоскостей.
b
c
М
а
Слайд 16Оформление доказательства:
I. Строим плоскость γ:
а) a ⊥ c, a ⊂
б) γ (а, b) (аксиома: если две различные прямые имеют общую точку, то через них можно провести плоскость).
II. Доказываем, что γ удовлетворяет признакам, указанным в определении перпендикулярных плоскостей:
а) γ ⊥ c (по признаку перпендикулярности прямой и плос-кости, так как с ⊥ а по построению, а b ⊥ с по определению перпендикулярности прямой и плоскости);
б) a ⊥ b (по определению перпендикулярности прямой и плоскости).
Значит, α ⊥ β (по определению перпендикулярных плоскостей).