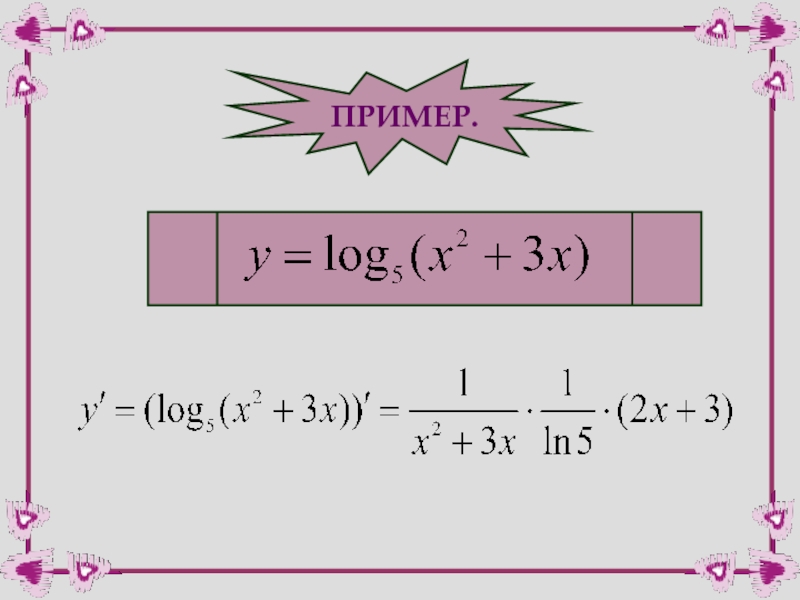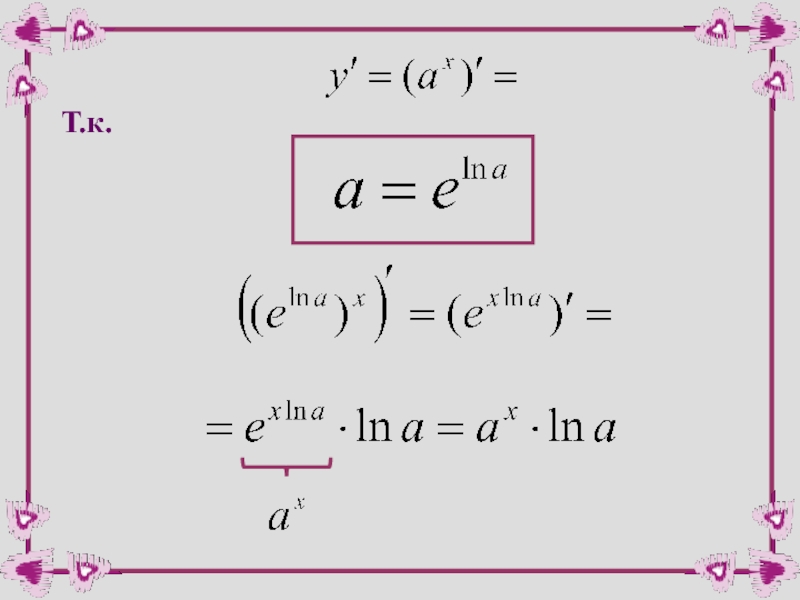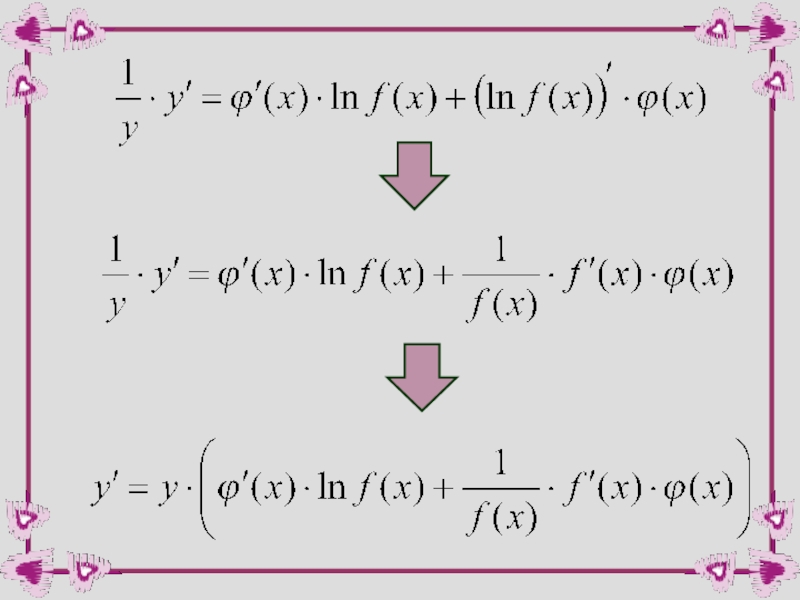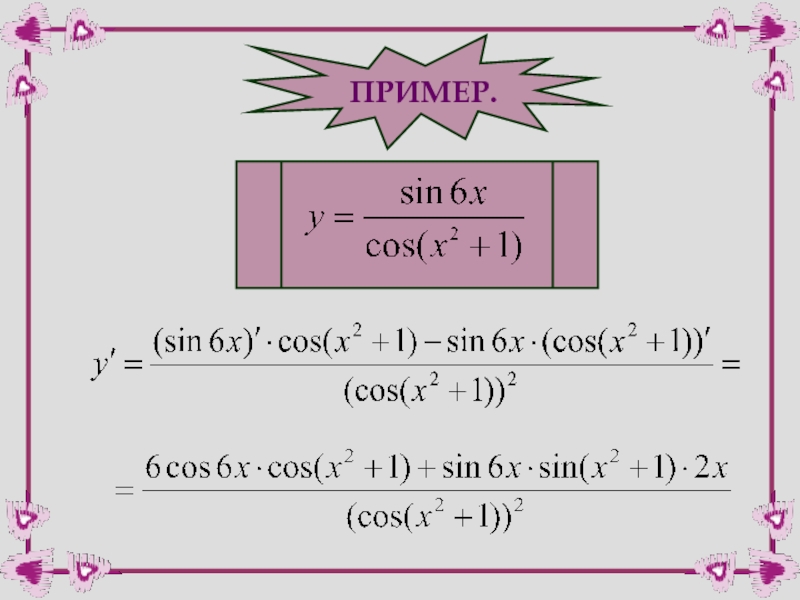- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производные элементарных функции презентация
Содержание
- 1. Производные элементарных функции
- 2. Дадим аргументу х приращение Δх и найдем
- 3. Составляем отношение Находим предел этого отношения: Сделаем замену:
- 4. Тогда В силу непрерывности логарифмической функции меняем местами знаки логарифма и предела:
- 5. производная натурального логарифма Для сложной функции:
- 6. ПРИМЕР.
- 7. Найдем производную для общего случая логарифмической функции:
- 8. По свойству логарифма Тогда Отсюда окончательно имеем
- 9. производная логарифмической функции Для сложной функции:
- 10. ПРИМЕР.
- 11. 2. Производная показательной функции Сначала рассмотрим частный случай показательной функции:
- 12. Логарифмируем обе части равенства по основанию e:
- 13. производная экспоненты Для сложной функции:
- 14. Кривая (экспонента) обладает свойством: в каждой
- 15. ПРИМЕР.
- 16. Найдем производную для общего случая показательной функции:
- 17. Т.к.
- 18. производная показательной функции Для сложной функции:
- 19. ПРИМЕР.
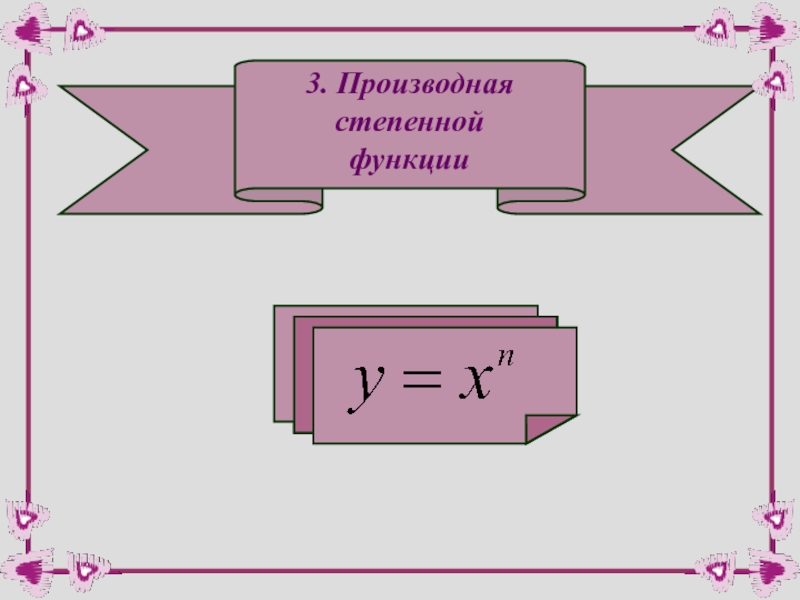
- 20. 3. Производная степенной функции
- 21. Логарифмируем обе части равенства по основанию e: Дифференцируем обе части равенства по х:
- 22. Отсюда выражаем искомую производную: Т.к. то окончательно получаем:
- 23. производная степенной функции Для сложной функции:
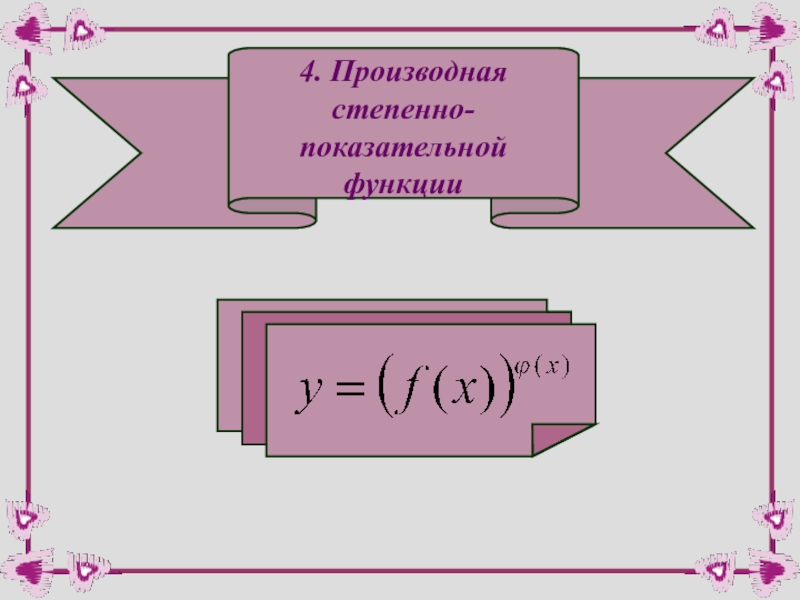
- 24. 4. Производная степенно- показательной функции
- 25. Логарифмируем обе части равенства по основанию e:
- 27. Т.к. то окончательно получаем:
- 28. Чтобы продифференцировать степенно-показательную функцию, ее
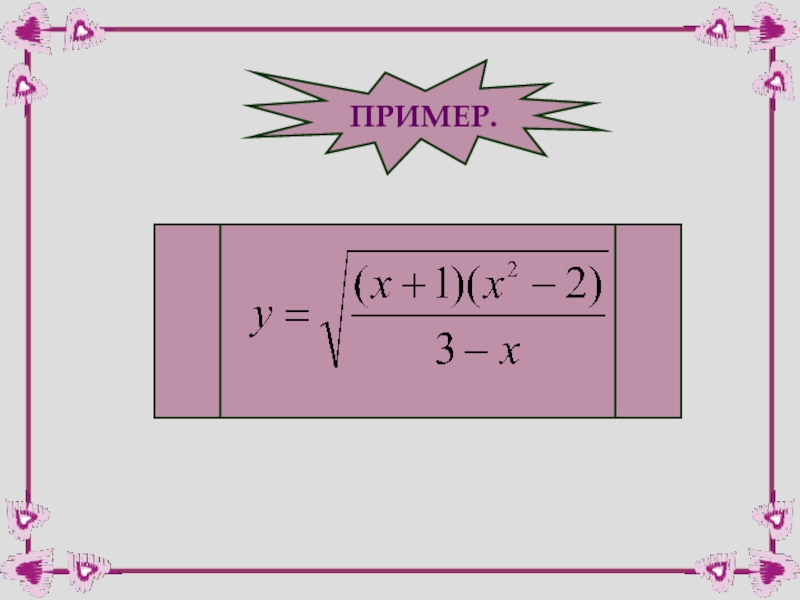
- 29. ПРИМЕР.
- 30. ЗАМЕЧАНИЕ Производная логарифмической функции называется логарифмической
- 31. ПРИМЕР.
- 32. Логарифмируем обе части равенства по основанию e: Используем свойства логарифма:
- 33. Дифференцируем обе части равенства по х:
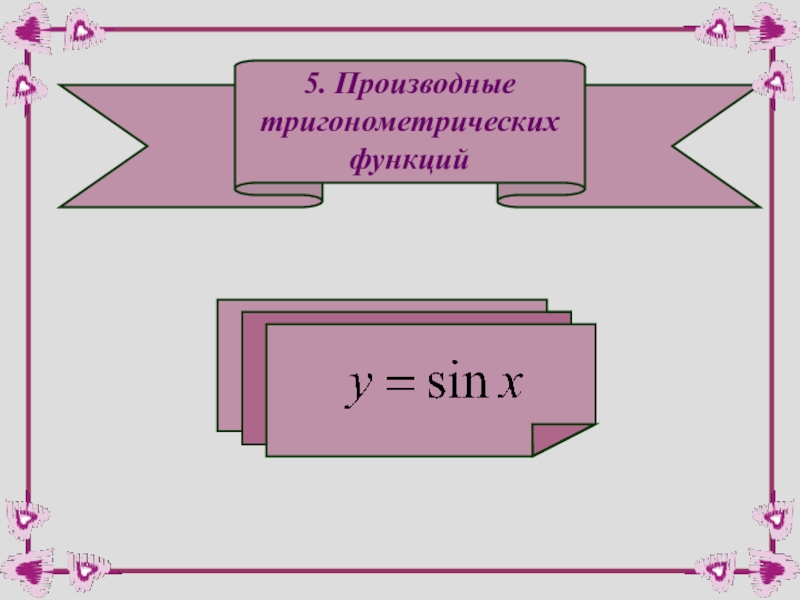
- 34. 5. Производные тригонометрических функций
- 35. Дадим аргументу х приращение Δх и найдем
- 36. Составляем отношение Находим предел этого отношения:
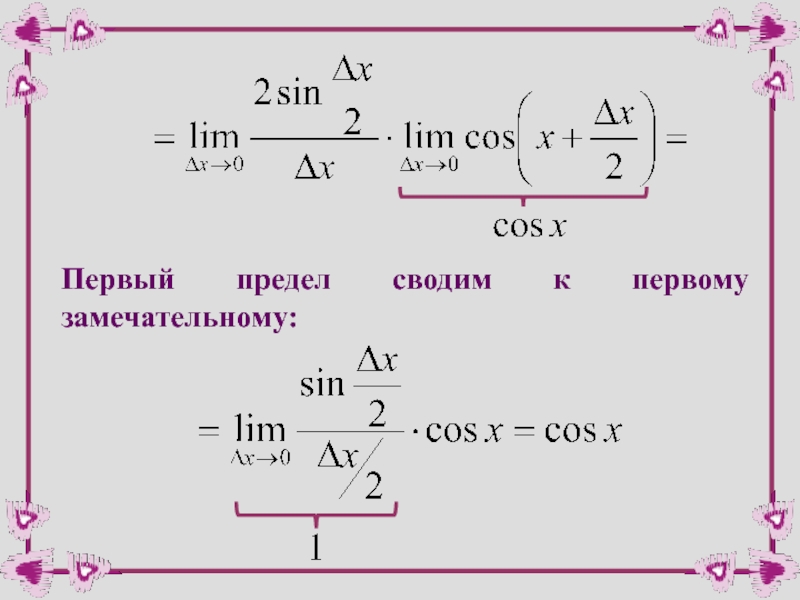
- 37. Первый предел сводим к первому замечательному:
- 38. производная синуса Для сложной функции:
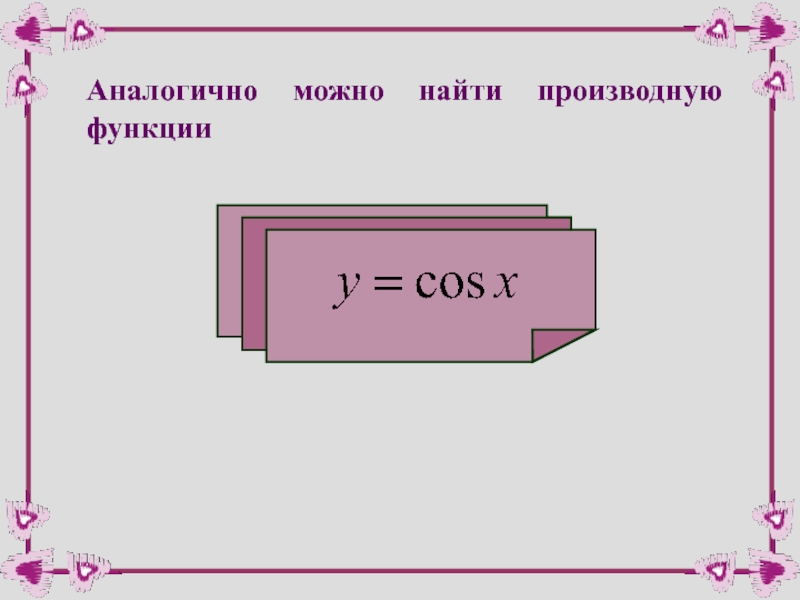
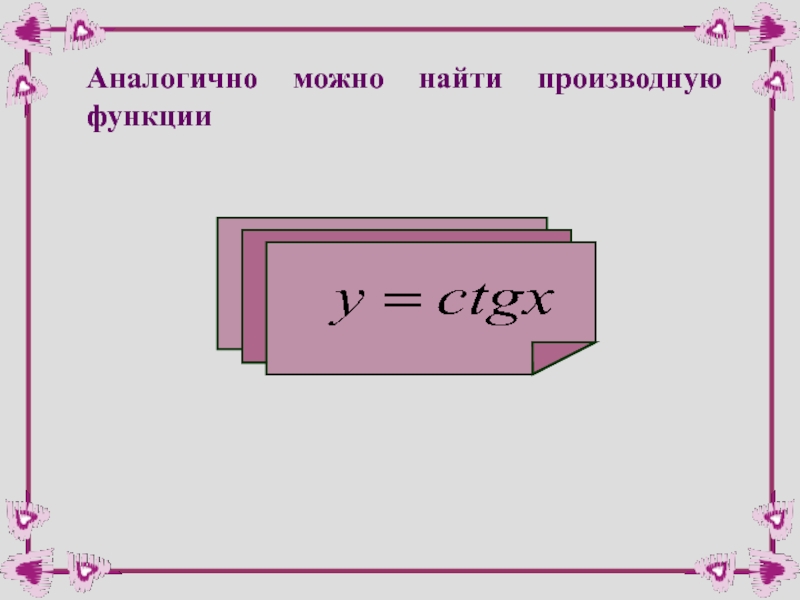
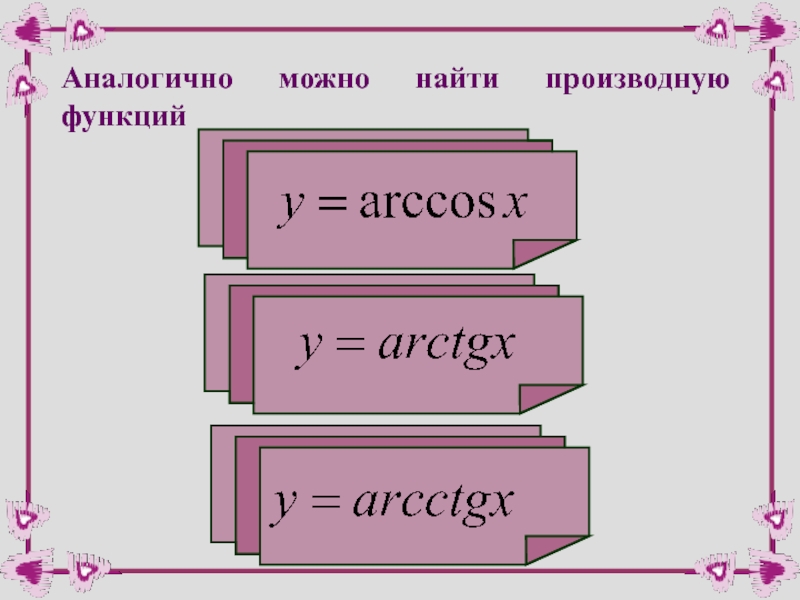
- 39. Аналогично можно найти производную функции
- 40. производная косинуса Для сложной функции:
- 41. ПРИМЕР.
- 42. Найдем производную функции
- 43. Находим производную дроби:
- 44. производная тангенса Для сложной функции:
- 45. Аналогично можно найти производную функции
- 46. производная котангенса Для сложной функции:
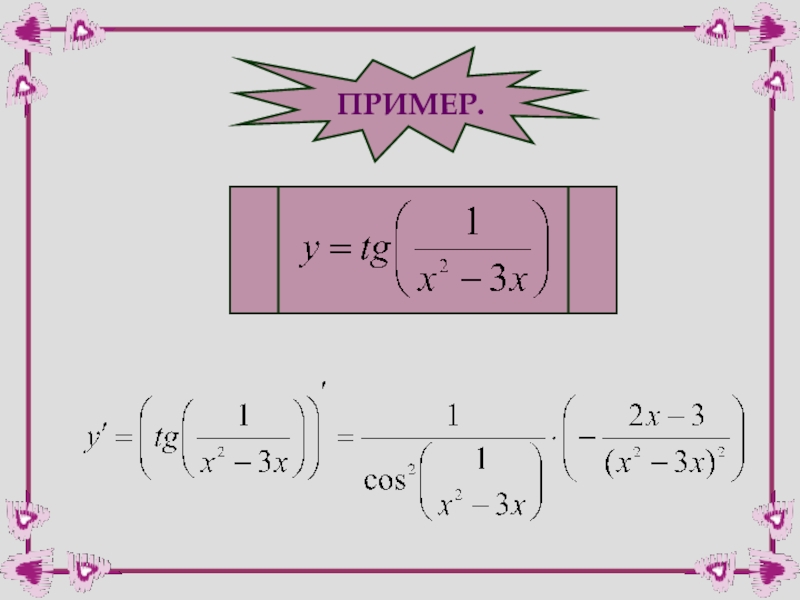
- 47. ПРИМЕР.
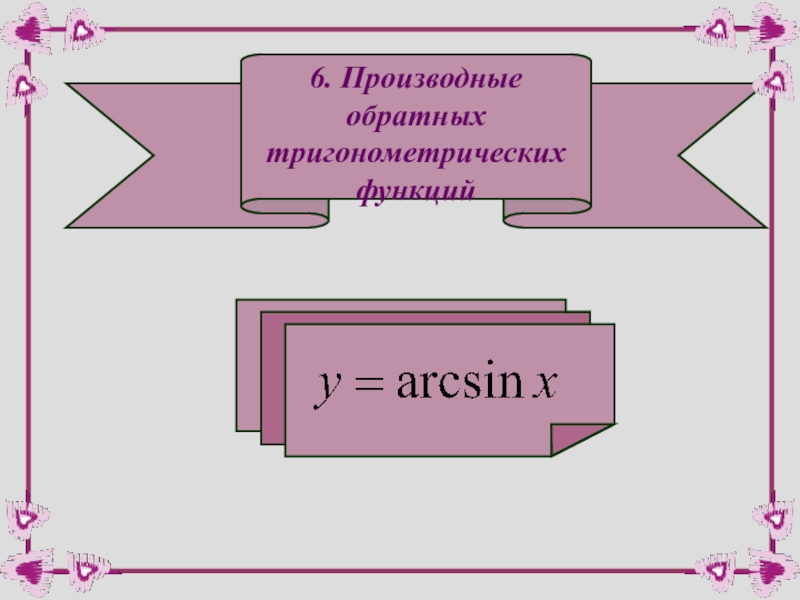
- 48. 6. Производные обратных тригонометрических функций
- 49. Обратной к ней функцией будет Используем правило
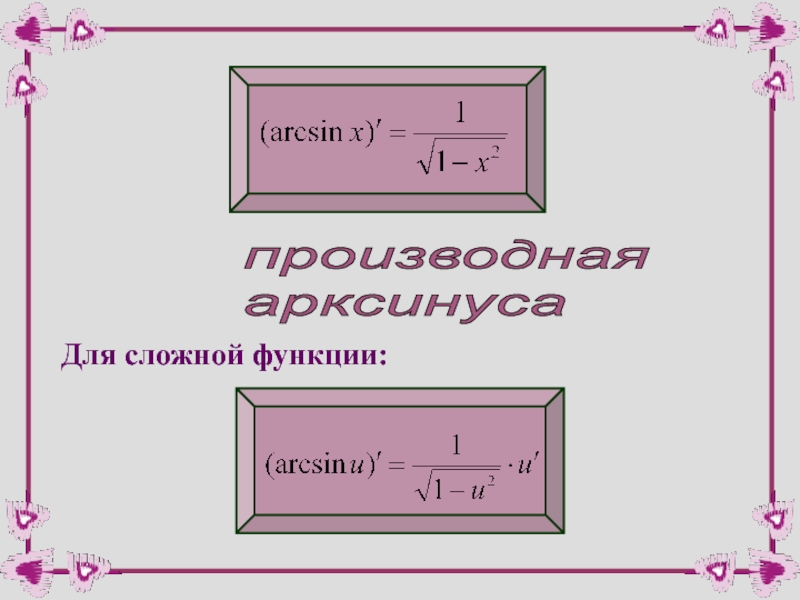
- 50. производная арксинуса Для сложной функции:
- 51. Аналогично можно найти производную функций
- 52. производная арккосинуса Для сложной функции:
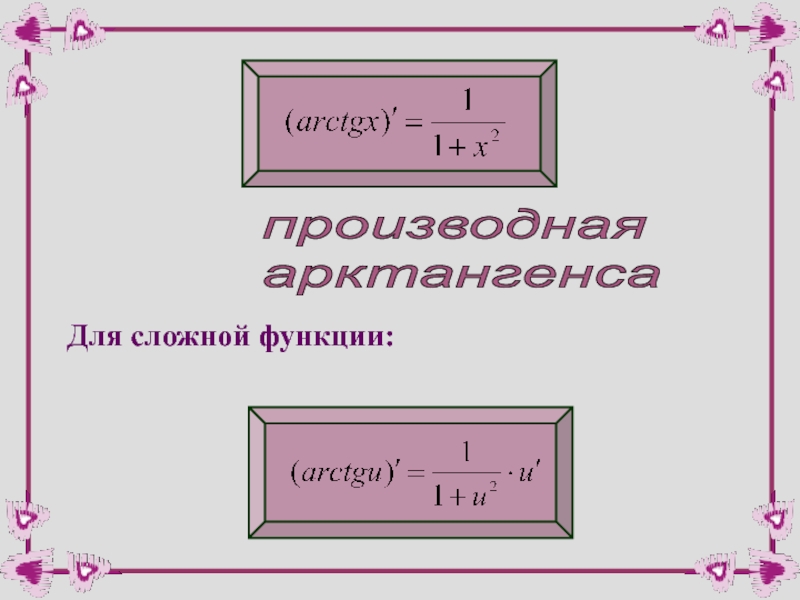
- 53. производная арктангенса Для сложной функции:
- 54. производная арккотангенса Для сложной функции:
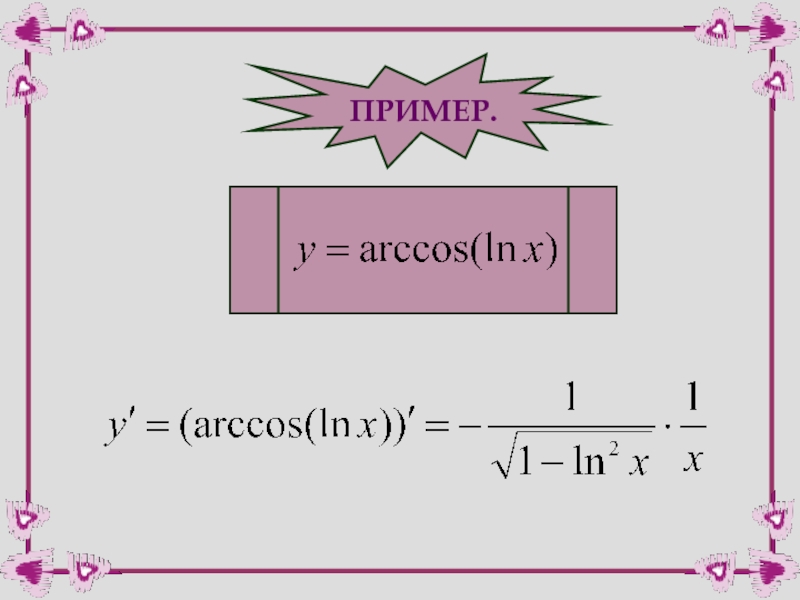
- 55. ПРИМЕР.
Дадим аргументу х приращение Δх и найдем значение функции y+Δy: Находим приращение функции Используем схему нахождения производной: По свойству логарифма:
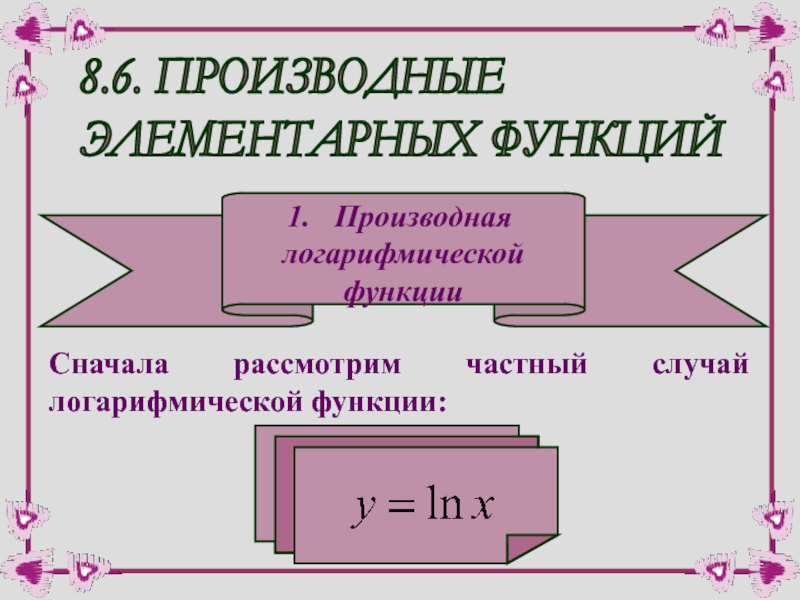
Слайд 18.6. ПРОИЗВОДНЫЕ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Производная
логарифмической
функции
Сначала рассмотрим частный случай логарифмической функции:
Слайд 2Дадим аргументу х приращение Δх и найдем значение функции y+Δy:
Находим
приращение функции
Используем схему нахождения производной:
По свойству логарифма:
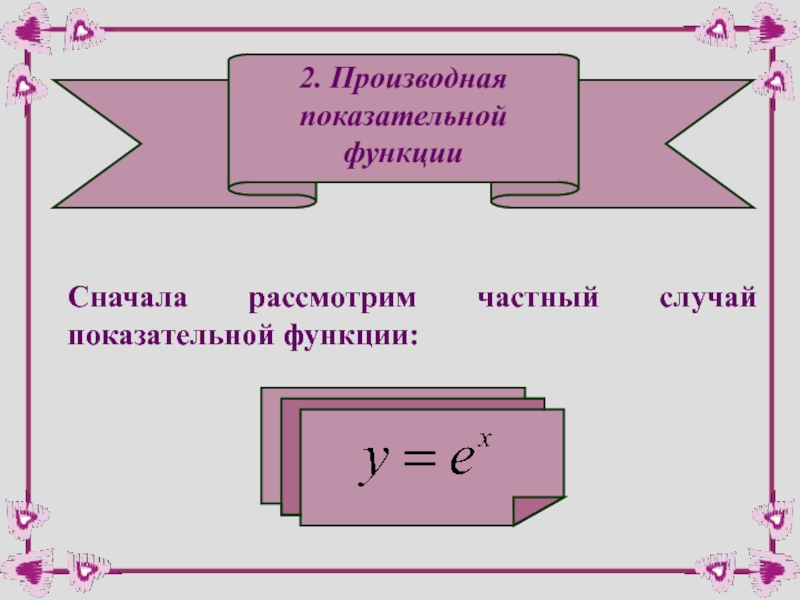
Слайд 112. Производная
показательной
функции
Сначала рассмотрим частный случай показательной функции:
Слайд 12Логарифмируем обе части равенства по основанию e:
Дифференцируем обе части равенства по
х:
Отсюда выражаем искомую производную:
Т.к.
то окончательно получаем:
Слайд 14Кривая
(экспонента) обладает свойством: в каждой точке х ордината у равна
угловому коэффициенту касательной к кривой в этой точке:
Слайд 25Логарифмируем обе части равенства по основанию e:
Дифференцируем обе части равенства по
х, учитывая, что в правой части стоит произведение:
Слайд 28Чтобы продифференцировать
степенно-показательную функцию,
ее сначала нужно
продифференцировать как
показательную функцию,
а затем
как степенную и полученные
результаты сложить.
как степенную и полученные
результаты сложить.
Слайд 30ЗАМЕЧАНИЕ
Производная логарифмической функции
называется логарифмической производной. Ее удобно использовать для дифференцирования функции,
выражение которой существенно упрощается при логарифмирования.
Слайд 35Дадим аргументу х приращение Δх и найдем значение функции y+Δy:
Находим
приращение функции
Используем схему нахождения производной:
Распишем разность синусов:
Слайд 49Обратной к ней функцией будет
Используем правило дифференцирования обратной функции:
Теперь нужно выразить
у через х с помощью основного тригонометрического соотношения:
Эта производная не существует при
