- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Принятие решений в условиях определенности презентация
Содержание
- 1. Принятие решений в условиях определенности
- 2. Принятие решений в условиях определенности Принятие
- 3. Рассмотрим проблему выбора наилучших решений. Она возникает
- 4. 1. Результат (альтернатива)
- 5. 2. Транзитивность Если
- 6. 3. Линейность Если некоторый результат
- 7. 4. Адитивность Если
- 8. 5. Аналогично Если имеем n – результатов
- 9. Отношения на множестве альтернатив Отношение слабого предпочтения
- 10. Для двух альтернатив
- 11. I. Случай Определяем, какой результат более предпочтителен
- 12. ІІ. Случай Определяем величину
- 13. ІІІ. Случай Упорядочивают все результаты по убыванию
- 14. ПРИМЕР Пусть эксперт упорядочивает пять результатов
- 15. РЕШЕНИЕ Подставим начальные оценки в неравенство 7):
- 16. В случаях, когда Р.
- 17. Какие свойства должны удовлетворять эквивалентные целевые функции
- 18. Презентация на тему : Принятие решений в
Слайд 1Презентация на тему : Принятие решений в условиях определенности.
Студенты 333 группы
Трацевская Анастасия
Коровянская Ангелина
Корнилова Наталья
Бобровский Андрей
Слайд 2Принятие решений в условиях определенности
Принятие решений в условиях определенности характеризуется однозначной
Слайд 3Рассмотрим проблему выбора наилучших решений. Она возникает тогда, когда существует некоторое
Слайд 41. Результат (альтернатива)
оказывается предпочтительнее альтернативы
, где -
полезности альтернатив
и
соответственно
Слайд 74. Адитивность
Если
Слайд 9Отношения на множестве альтернатив
Отношение слабого предпочтения – «не хуже», обозначаемое знаком
Отношение строгого предпочтения, обозначаемое знаком ≻
Отношение эквивалентности (равноценности), обозначаемое знаком ~
Слайд 10Для двух альтернатив будем говорить,что
x1≽x2 тогда и только тогда, когда
тогда и только тогда, когда
тогда и только тогда, когда
Слайд 11I. Случай
Определяем, какой результат более предпочтителен для лица, принимающего решение. Пусть
Определяем
Оцениваем соотношение между полезностями результатов и . Для этого примем полезность
, тогда ;
Слайд 12ІІ. Случай
Определяем величину из условия
Аналогично определяем
Положив полезность наименее предпочтительного результата равной 1, находим:
…,
Слайд 13ІІІ. Случай
Упорядочивают все результаты по убыванию предпочтительности. Пусть
Составляют таблицу возможных комбинаций результатов, а затем устанавливают их предпочтение относительно отдельных результатов
Приписывают начальные оценки полезностям отдельных результатов . Подставляют начальные оценки в последнее соотношение. Если оно удовлетворяется, то оценки не изменяют. В противном случае производят коррекцию полезностей так, чтобы это соотношение удовлетворялось
Процесс коррекции продолжается до тех пор, пока не образуется система оценок , которая будет удовлетворять всем соотношениям
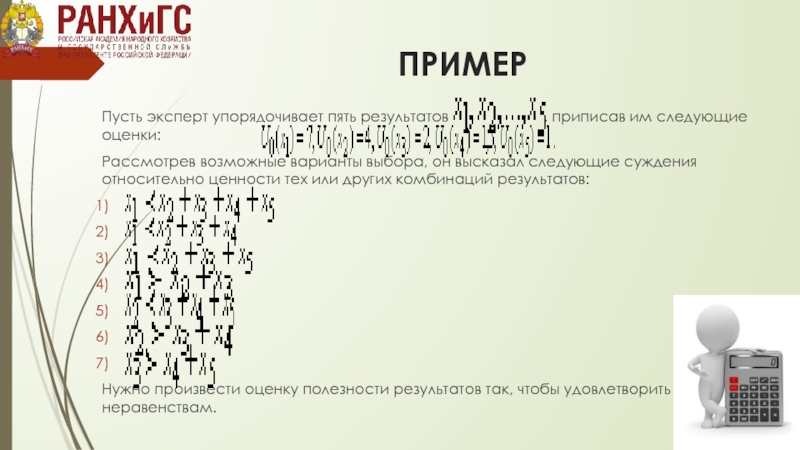
Слайд 14ПРИМЕР
Пусть эксперт упорядочивает пять результатов
Рассмотрев возможные варианты выбора, он высказал следующие суждения относительно ценности тех или других комбинаций результатов:
Нужно произвести оценку полезности результатов так, чтобы удовлетворить всем неравенствам.
Слайд 15РЕШЕНИЕ
Подставим начальные оценки в неравенство 7):
Следовательно, неравенство 7) не удовлетворяется. Изменяем
Это неравенство также не удовлетворяется.
Положим . При этом неравенство 5) удовлетворяется.
Проверим неравенство 4): . Оно не выполняется. Поэтому возьмем . Теперь неравенства 1), 2), 3) удовлетворяются.
Проверим еще раз неравенства 6) и 7) при измененных значениях полезностей:
. Оба неравенства выполняются.
Запишем окончательные оценки полезности результатов:
Слайд 16В случаях, когда Р. Черчмен , Р. Акоф
Слайд 17Какие свойства должны удовлетворять эквивалентные целевые функции устанавливает такая простая теорема
ТЕОРЕМА 1.1. ДЛЯ того чтобы целевые функции и были эквивалентными, достаточно, чтобы существовало такое монотонное преобразование , переводящее область значенийфункции в область значений функции так, что для всего множества допустимых альтернатив. При этом, если обе целевые функции максимизируются, то преобразование должно быть монотонно возрастающей функцией, а если нет, то монотонно убывающей функцией.
Слайд 18Презентация на тему : Принятие решений в условиях определенности.
Студенты 333 группы
Трацевская Анастасия
Коровянская Ангелина
Корнилова Наталья
Бобровский Андрей