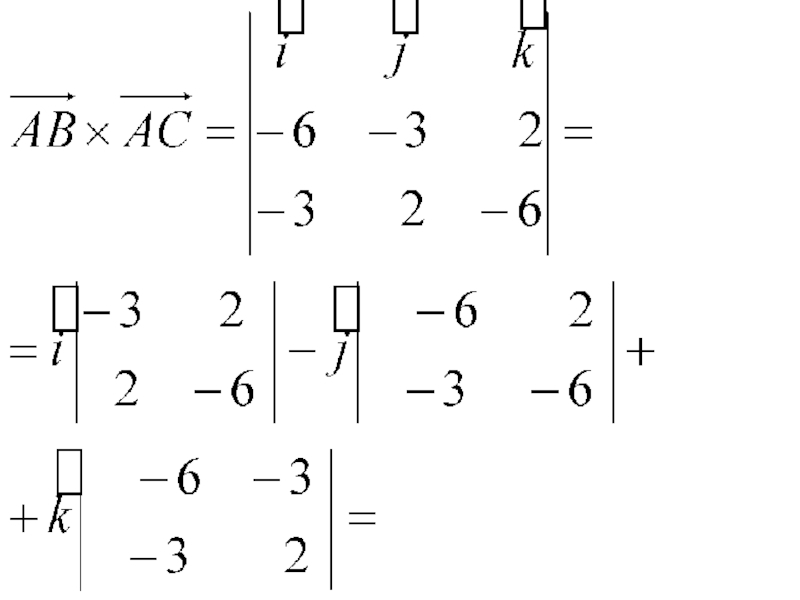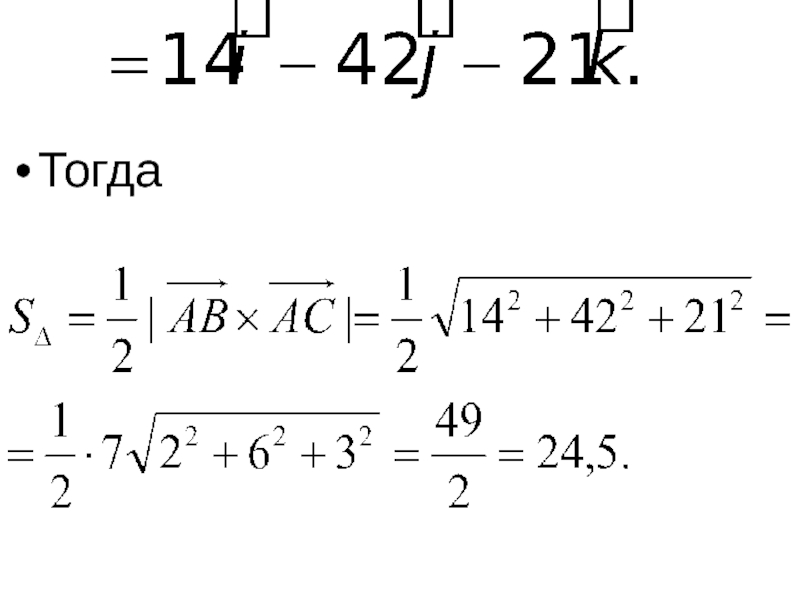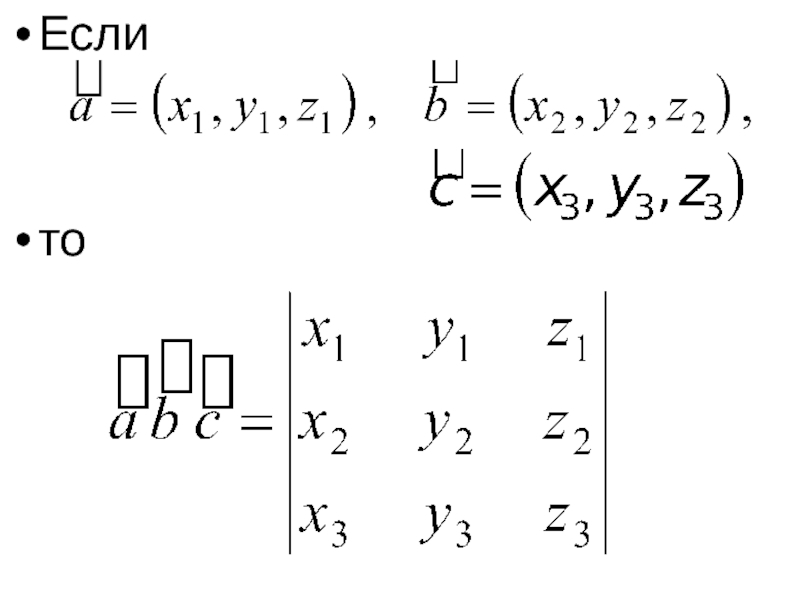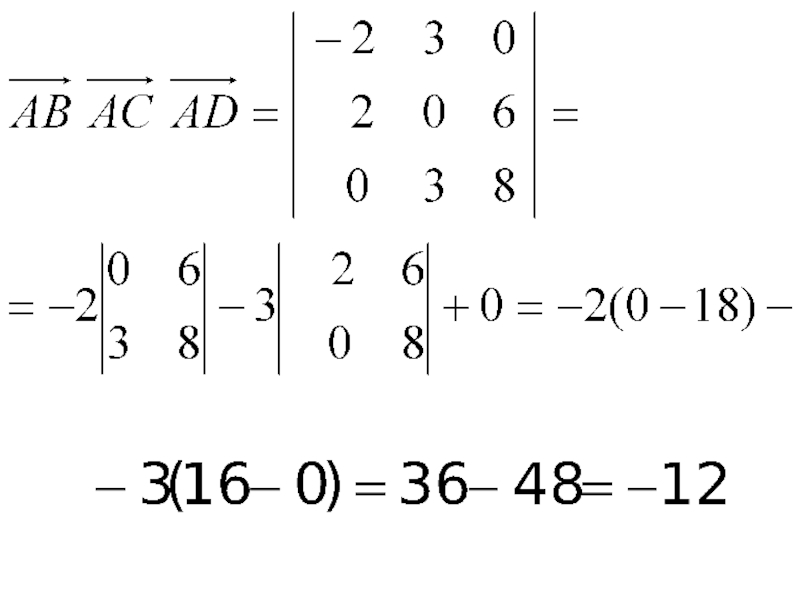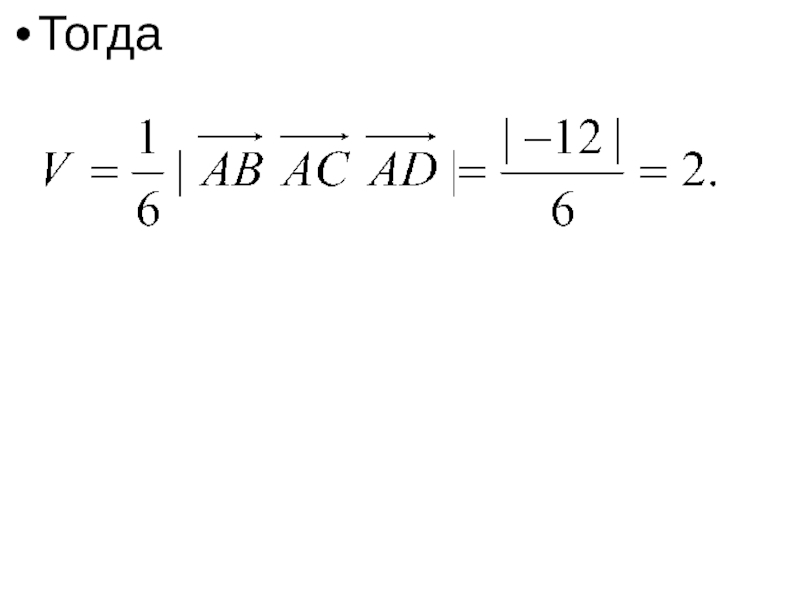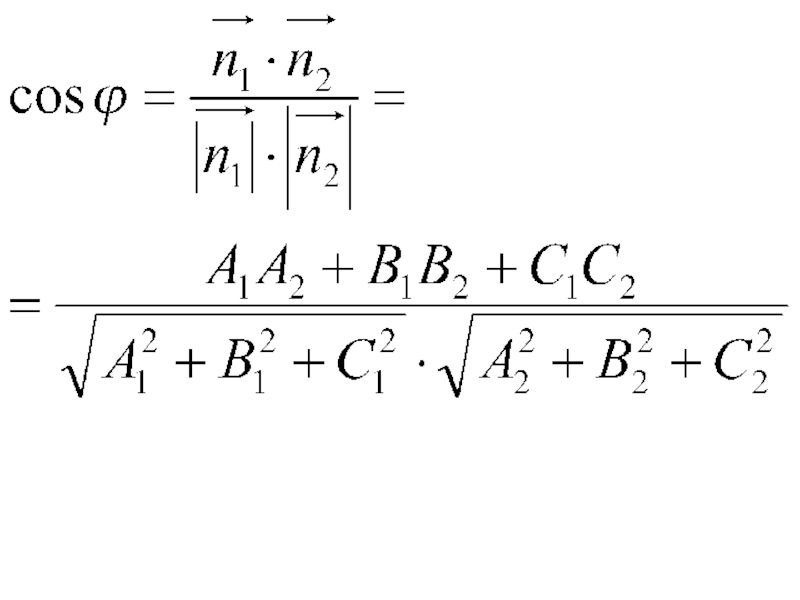- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторное произведение векторов презентация
Содержание
- 1. Векторное произведение векторов
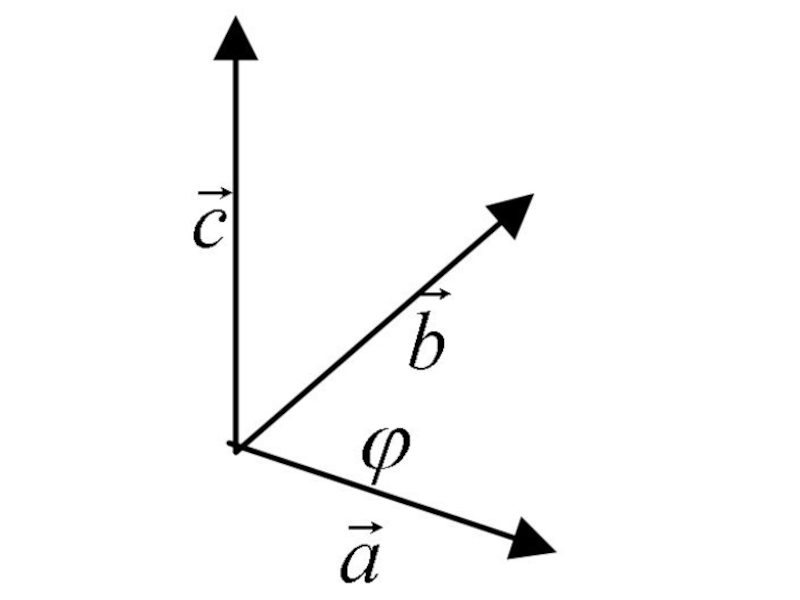
- 2. 1. 2. 3. тройка
- 4. Свойства векторного произведения 1. 2. 3. 4.
- 5. Если то
- 6. Приложения векторного произведения к задачам геометрии и механики.
- 7. Площадь параллелограмма (геометрический смысл векторного произведения). Площадь треугольника
- 8. Момент силы (механический смысл векторного произведения). Пусть
- 9. Пример. Вычислить площадь треугольника с вершинами A(7,3,4), B(1,0,6) , C(4,5,-2).
- 10. Решение. Находим векторы Вычисляем векторное произведение
- 12. Тогда
- 13. Смешанное произведение векторов Определение. Смешанным произведением
- 14. Если то
- 15. Приложения смешанного произведения к задачам геометрии
- 16. Объём параллелепипеда, построенного на векторах
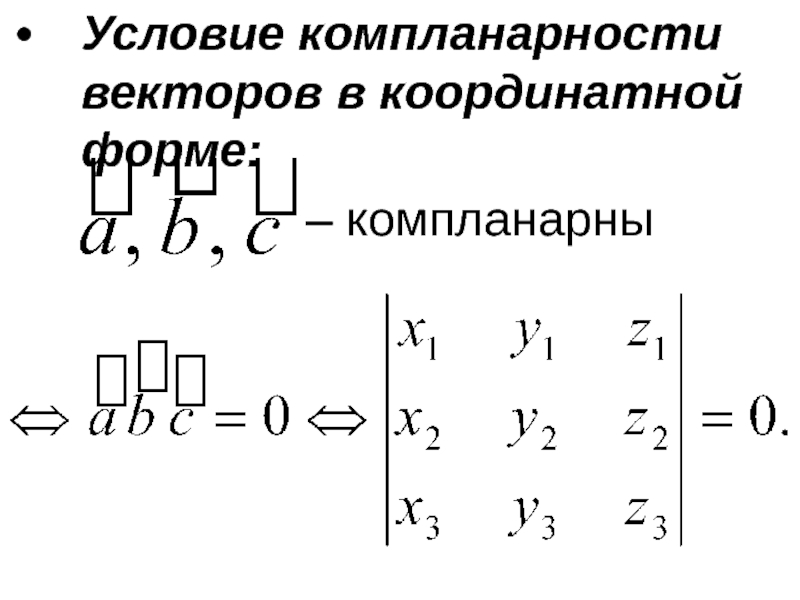
- 17. Условие компланарности векторов в координатной форме:
- 18. Пример. Вычислить объём пирамиды с вершинами в точках A(2,0,0), B(0,3,0), C(4,0,6), D(2,3,8).
- 19. Решение. Находим векторы
- 21. Тогда
- 23. Модуль 2 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- 24. Плоскость и её основные уравнения Рассмотрим
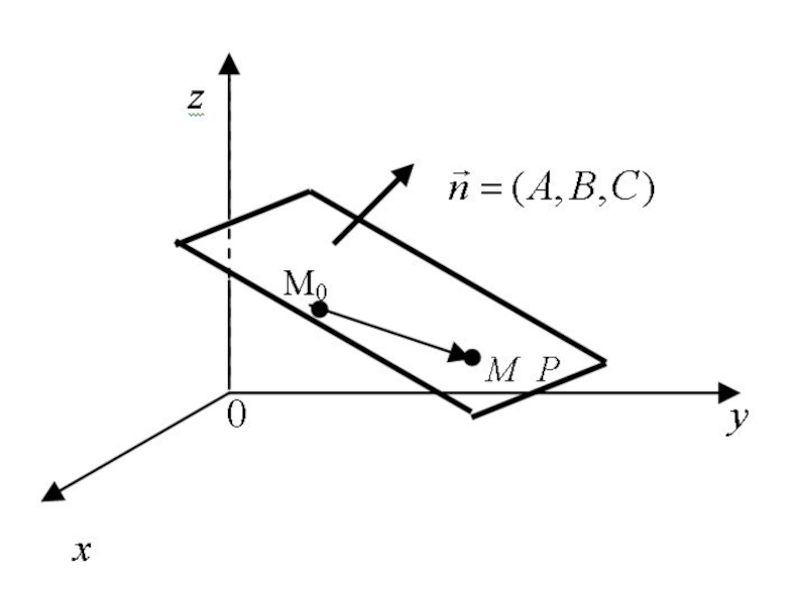
- 25. Положение плоскости вполне определяется точкой и вектором нормали
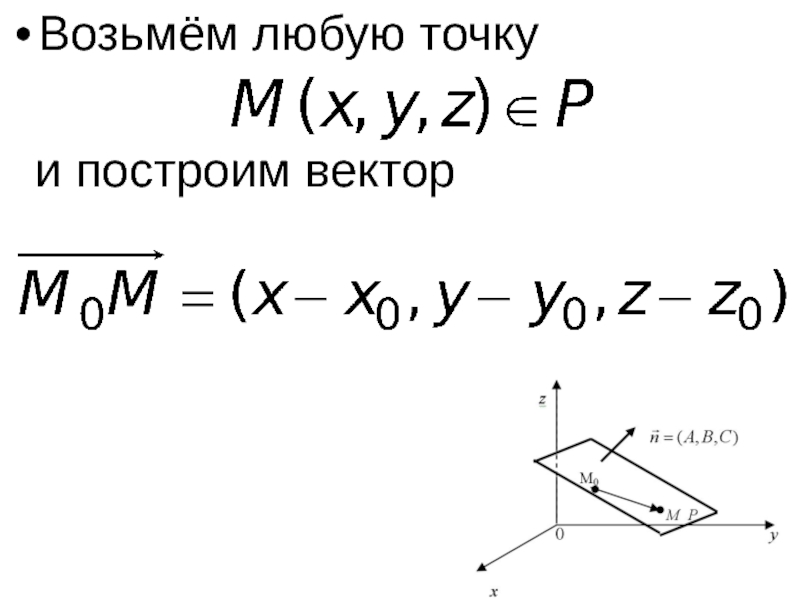
- 27. Возьмём любую точку и построим вектор
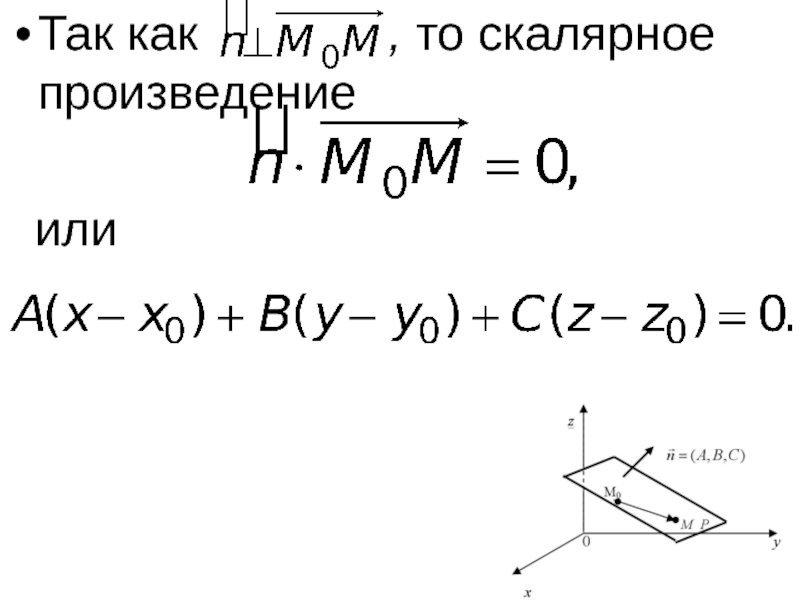
- 28. Так как
- 29. Получили уравнение плоскости, заданной точкой
- 30. Если в уравнении раскрыть
- 31. Теорема. Всякое уравнение вида определяет некоторую плоскость в пространстве.
- 32. Если в этом уравнении какой-либо из коэффициентов
- 33. Например, при A = 0 плоскость By
- 34. Пусть в уравнении ни
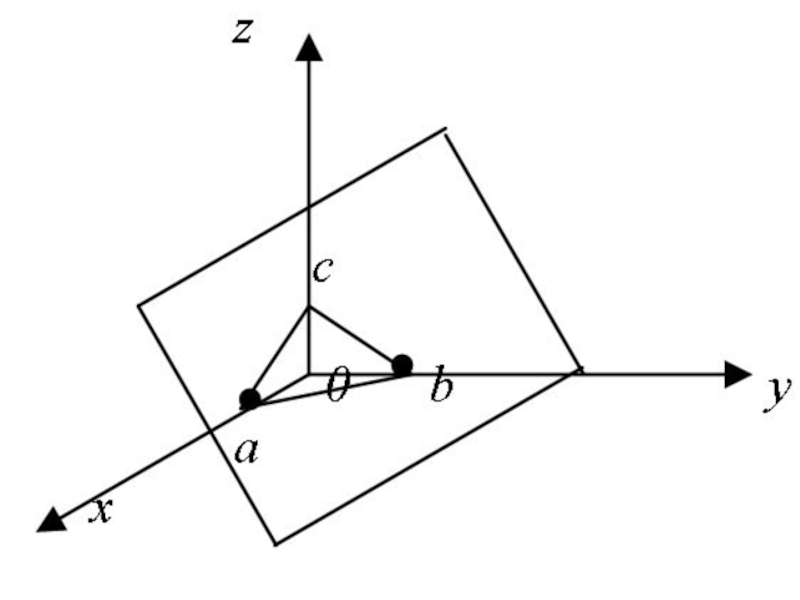
- 35. Получим уравнение плоскости в отрезках:
- 36. где a, b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат
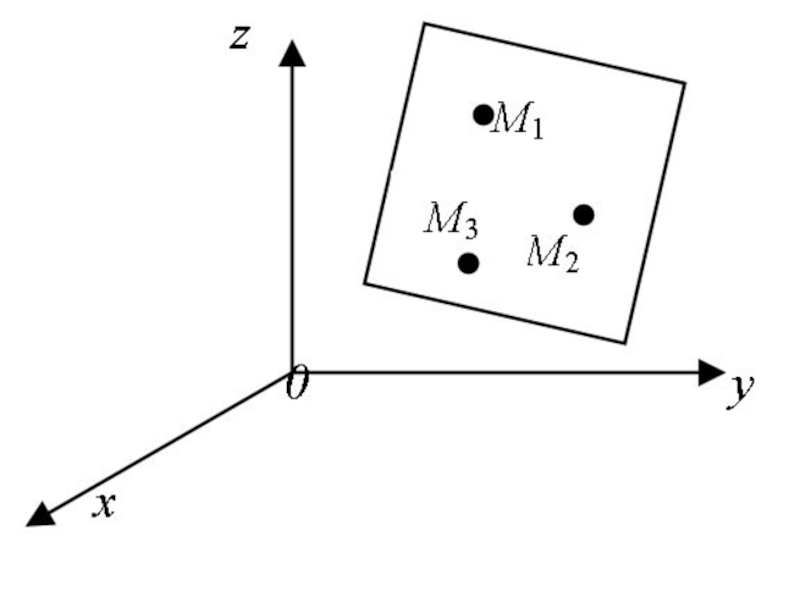
- 38. Если три точки
- 40. Уравнение плоскости, проходящей через три точки, имеет вид:
- 41. Пусть даны две плоскости и
- 43. Расстояние d от точки
- 44. Пример. Даны две точки
- 45. Решение. Поскольку искомая плоскость перпендикулярна вектору
- 47. Подставив теперь в уравнение
- 48. или
1. 2. 3. тройка – правая (т.е. при наблюдении из конца вектора кратчайший поворот от к
Слайд 1Векторное произведение векторов
Векторным произведением векторов и
называется вектор , обозначаемый , который удовлетворяет следующим трём условиям:
Слайд 21.
2.
3. тройка – правая (т.е.
при наблюдении из конца вектора кратчайший поворот от к виден совершающимся против часовой стрелки.
Слайд 8Момент силы (механический смысл векторного произведения).
Пусть точка А твердого тела закреплена,
а в точке В приложена сила . Тогда возникает вращающий момент
Слайд 13Смешанное произведение векторов
Определение. Смешанным произведением трех векторов
называется число
Слайд 16Объём параллелепипеда, построенного на векторах
(геометрический смысл смешанного произведения).
Объём пирамиды
Объём пирамиды
Слайд 18Пример. Вычислить объём пирамиды с вершинами в точках A(2,0,0), B(0,3,0), C(4,0,6),
D(2,3,8).
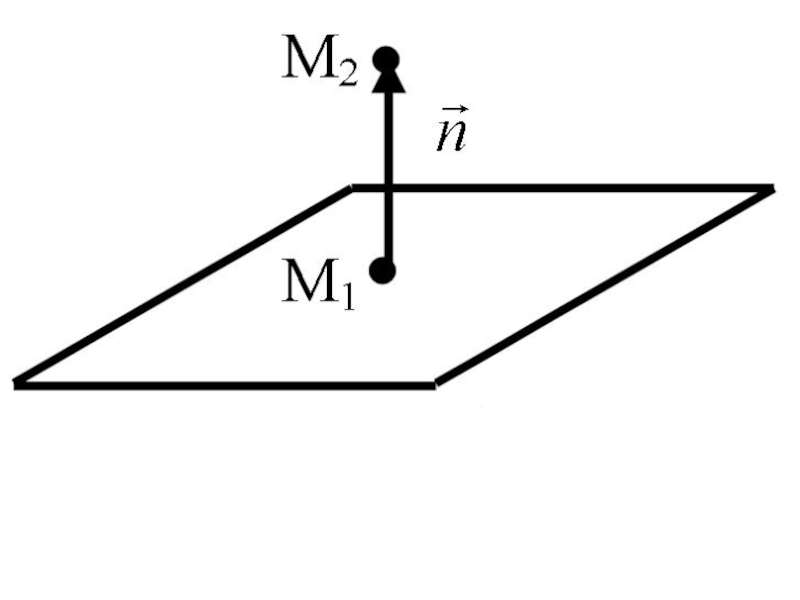
Слайд 24Плоскость и её основные уравнения
Рассмотрим плоскость P в прямоугольной декартовой
системе координат.
Слайд 32Если в этом уравнении какой-либо из коэффициентов A, B, C равен
нулю, то плоскость расположена параллельно той оси, координата которой отсутствует в уравнении.
Слайд 33Например, при A = 0 плоскость By + Cz + D
= 0 параллельна оси Ox; при A = B = 0 плоскость Cz + D = 0 параллельна осям Ox и Oy, т.е. плоскости xOy и т.д.
Слайд 34Пусть в уравнении
ни один из коэффициентов не равен 0.
Перепишем это уравнение в виде
разделим обе части этого равенства на - D и обозначим
разделим обе части этого равенства на - D и обозначим
Слайд 38Если три точки
не лежат на одной прямой, то через
эти точки проходит единственная плоскость:
Слайд 41Пусть даны две плоскости
и
Угол φ между двумя плоскостями равен
углу между их векторами нормали:
Слайд 44Пример. Даны две точки
Записать уравнение плоскости, проходящей через точку
M1 перпендикулярно вектору
Слайд 45Решение. Поскольку искомая плоскость перпендикулярна вектору
, то в качестве вектора нормали возьмем вектор
